[Bèta wiskunde] Huiswerk- en vragentopic

6 keer de pdf van de standaardnormale verdeling geïntegreerd over de reële getallen (ook wel Gaussverdeling)

quote:

Op dinsdag 12 juni 2012 21:55 schreef thenxero het volgende:


6 keer de pdf van de standaardnormale verdeling geïntegreerd over de reële getallen (ook wel Gaussverdeling)

Wel een gelukje. Het getal 6 had ik nou net uitgeprint, geplastificeerd en uitgeknipt. Mis ik de /pi, kudt.

Prachtig!

jaja harde struggles op de middelbare school

quote:

Op dinsdag 12 juni 2012 22:13 schreef thenxero het volgende:
jaja harde struggles op de middelbare school

Een mondeling examen wiskunde B, wie heeft dat verzonnen?

quote:

Op dinsdag 12 juni 2012 21:55 schreef thenxero het volgende:


6 keer de pdf van de standaardnormale verdeling geïntegreerd over de reële getallen (ook wel Gaussverdeling)

Ja, moet hij natuurlijk wél kunnen vertellen hoe je dit aan kunt tonen. Daar zijn een hoop manieren voor die minder afgezaagd zijn dan de bekende conversie naar een dubbelintegraal en dan transformatie naar poolcoördinaten. Misschien is dit artikel aardig om mee te beginnen.

quote:

Op dinsdag 12 juni 2012 22:33 schreef Riparius het volgende:

[..]

Ja, moet hij natuurlijk wél kunnen vertellen hoe je dit aan kunt tonen. Daar zijn een hoop manieren voor die minder afgezaagd zijn dan de bekende conversie naar een dubbelintegraal en dan transformatie naar poolcoördinaten. Misschien is dit artikel aardig om mee te beginnen.

Daar wilde ik me nog in gaan verdiepen.
Maargoed, ik heb m'n klok af. Morgen ga ik me in zowel deze link als in het probleem van de integraal over 1/cos(x) verdiepen. Ik blijf benieuwd naar wat jij allemaal gestudeerd hebt (ook al wil je het niet zeggen.)
http://s7.postimage.org/sduet4zih/2012_06_12_22_36_30.jpg


Mensen die een beetje opletten zullen direct zien dat de Gaussverdeling boven de afbeelding van Riemann staat, terwijl Carl Friedrich opgeschoven is naar de zeven. Toeval.

[ Bericht 2% gewijzigd door Muiroe op 12-06-2012 22:56:46 ]

Pics van de klok?

quote:

Op dinsdag 12 juni 2012 22:44 schreef Muiroe het volgende:

[..]
Ik blijf benieuwd naar wat jij allemaal gestudeerd hebt (ook al wil je het niet zeggen.)

Het lijkt me vrij duidelijk dat Riparius wiskunde gestudeerd heeft.

quote:

Op dinsdag 12 juni 2012 22:48 schreef thenxero het volgende:

[..]

Het lijkt me vrij duidelijk dat Riparius wiskunde gestudeerd heeft.

Ik las toevallig zijn post in een topic wat ging over Nederlands (hexameters meende ik). Toevallig legde ik dit uit zuivere interesse voor aan mijn docente Nederlands, die moest volgens mij heel diep teruggraven voordat ze het me uit kon leggen. En niet iedere wiskundige heeft wiskunde gestudeerd. Dit volgt wel uit Riparius zijn voorbeeld over Argand, wiens publicatie over de complexe getallen in zijn eigen boekhandeltje te vinden was. (als ik het goed begrepen heb)

quote:

Op dinsdag 12 juni 2012 22:46 schreef Ron.Jeremy het volgende:
Pics van de klok?

Volgens mij ben je een post te laat.

edit

Ik zie geen plaatje, kan aan mij liggen...

EDIT:

Dat plaatje zie ik dan weer niet

quote:

Op dinsdag 12 juni 2012 22:33 schreef Riparius het volgende:

[..]

Ja, moet hij natuurlijk wél kunnen vertellen hoe je dit aan kunt tonen. Daar zijn een hoop manieren voor die minder afgezaagd zijn dan de bekende conversie naar een dubbelintegraal en dan transformatie naar poolcoördinaten. Misschien is dit artikel aardig om mee te beginnen.

Die heeft de docent bij infi A ook een keer voorgedaan, eens kijken of ik er nog iets van snap.

quote:

Op dinsdag 12 juni 2012 23:54 schreef kutkloon7 het volgende:

[..]

Die heeft de docent bij infi A ook een keer voorgedaan, eens kijken of ik er nog iets van snap.

Prof. Hogendijk?

Goed, ik ben dat artikel over de Secant aan het lezen. Het stuk wat ik niet begrijp komt meteen na figuur 1, ofwel het bovenste stukje. Wat is een loxodrome precies, en wat heeft secθ hiermee te maken?

quote:

Op woensdag 13 juni 2012 12:14 schreef Muiroe het volgende:
Goed, ik ben dat artikel over de Secant aan het lezen. Het stuk wat ik niet begrijp komt meteen na figuur 1, ofwel het bovenste stukje. Wat is een loxodrome precies, en wat heeft secθ hiermee te maken?

Een loxodroom is een koerslijn (in het engels ook rhumb line), oftewel een lijn op het aardoppervlak die alle meridianen onder een gelijke hoek snijdt. Als je een stereografische kaartprojectie maakt dan is de projectie van een loxodroom een logaritmische spiraal (!) met de noordpool of de zuidpool als centrum. Om nu te bereiken dat deze koerslijnen oftewel loxodromen op je kaartprojectie als rechte lijnen verschijnen (zodat je een zeekaart kunt maken waarop koersen als rechte lijnen zijn uit te zetten) heb je dus een hoekgetrouwe (conforme) projectie nodig waarbij tevens de meridianen als parallelle lijnen worden weergegeven. Lees ook het hoofdstuk A Mapmaker's Paradise uit het boekje van Maor en dit Wikipedia artikel, dan zal alles je wel duidelijker worden.

[ Bericht 1% gewijzigd door Riparius op 13-06-2012 13:39:34 ]

Vraagje, 4VWO:

(1/2)^-x+2 + 2^x+3 = 4 1/8
(2^-1)^-x+2 + 2^x+3 = 4 1/8
2^x-2 + 2^x+3 = 4 1/8
2^x-2 + 2^x-2 * 2^5 = 4 1/8


Het vetgedrukte begrijp ik niet
Hoezo wordt 2^x+3 vervangen voor 2^x-2 * 2^5

quote:

Op woensdag 13 juni 2012 00:02 schreef thenxero het volgende:

[..]

Prof. Hogendijk?

Ja. Wat een baas is dat trouwens, met zijn klankschaal .

quote:

Op woensdag 13 juni 2012 15:42 schreef MrBaas het volgende:
Vraagje, 4VWO:

(1/2)^-x+2 + 2^x+3 = 4 1/8
(2^-1)^-x+2 + 2^x+3 = 4 1/8
2^x-2 + 2^x+3 = 4 1/8
2^x-2 + 2^x-2 * 2^5 = 4 1/8


Het vetgedrukte begrijp ik niet
Hoezo wordt 2^x+3 vervangen voor 2^x-2 * 2^5

Heel eenvoudig, je kent toch wel de volgende rekenregel voor machten:

a^p+q = a^p∙a^q

Gebruik trouwens superscript voor je exponenten, dat is er niet voor niets.

-Riparius was me net voor-

quote:

Op woensdag 13 juni 2012 16:27 schreef Riparius het volgende:

[..]

Heel eenvoudig, je kent toch wel de volgende rekenregel voor machten:

a^p+q = a^p∙a^q

Gebruik trouwens superscript voor je exponenten, dat is er niet voor niets.

Begrijp het nog steeds niet.

quote:

Op woensdag 13 juni 2012 16:31 schreef MrBaas het volgende:

[..]

Begrijp het nog steeds niet.

De clou is hier dat je 2^x+3 herschrijft als het product 2^x-2∙2⁵ omdat je dan in het linkerlid van je vergelijking een factor 2^x-2 buiten haakjes kunt halen. En je ziet toch hopelijk wel in dat x + 3 = (x - 2) + 5.

Waarom is:

5^x-1

hetzelfde als:

5^x-2 * 5¹

Ik snap het nogsteeds niet helemaal. Hoe doe je dit nou ?

quote:

Op woensdag 13 juni 2012 19:03 schreef MrBaas het volgende:
Waarom is:

5^x-1

hetzelfde als:

5^x-2 * 5¹

Ik snap het nogsteeds niet helemaal. Hoe doe je dit nou ?

Met

a^p+q = a^p∙a^q

waarbij in dit geval

p=x-2 en q=1

quote:

Op woensdag 13 juni 2012 19:03 schreef MrBaas het volgende:
Waarom is:

5^x-1

hetzelfde als:

5^x-2 * 5¹

Ik snap het nogsteeds niet helemaal. Hoe doe je dit nou ?

Snap je de regel wel?
Anders moet je misschien even een voorbeeld nemen met getallen.
Als je bijvoorbeeld 2⁵ hebt, kan je dat natuurlijk schrijven als
2∙2∙2∙2∙2
=
2∙2 ∙ 2∙2∙2=2²∙2³
=
2 ∙ 2∙2∙2∙2=2∙2⁴

Dit kan je ook doen voor andere getallen dan 2 en 5, bijvoorbeeld het getal 'a' tot de macht 'm'. Dus als je eerst a tot een bepaalde macht m hebt (dit kan je dus schrijven als het product van m a's), kan je dat als het ware opsplitsen in een product van twee factoren, zolang het totaal aantal a's maar gelijk is aan m.

En als er in die exponent een variabele zit, maakt dat verder niet zoveel uit, je kan de macht nog steeds 'uitsplitsen' in twee factoren.

quote:

Op woensdag 13 juni 2012 16:14 schreef kutkloon7 het volgende:

[..]

Ja. Wat een baas is dat trouwens, met zijn klankschaal [ afbeelding ].

Haha, wel uniek ja. Eigenlijk moeten ze hem een keer een gong geven om aan te geven wanneer het college begint.

Ik snap nu wat het probleem was vroeger, wat de reeds bestaande mogelijkheden waren, wat een loxodrome en een grootcirkel / orthodrome is. Verder snap ik het verband tussen de straal van een breedtegraad en de afstand tot de evenaar. Ik snap alleen niet precies waar de integraal over de secans nu voor dient. Nu duurt een mondeling examen maar 40 minuten, waarvan ik misschien 5 minuten krijg om te presenteren, dus ik weet niet of ik ook nog toekom aan de Gudermann functie..

quote:

Op woensdag 13 juni 2012 23:39 schreef Muiroe het volgende:
Ik snap nu wat het probleem was vroeger, wat de reeds bestaande mogelijkheden waren, wat een loxodrome en een grootcirkel / orthodrome is. Verder snap ik het verband tussen de straal van een breedtegraad en de afstand tot de evenaar. Ik snap alleen niet precies waar de integraal over de secans nu voor dient. Nu duurt een mondeling examen maar 40 minuten, waarvan ik misschien 5 minuten krijg om te presenteren, dus ik weet niet of ik ook nog toekom aan de Gudermann functie..

Je begrijpt dat we een hoekgetrouwe (conforme) projectie nodig hebben waarbij bovendien de meridianen als parallelle lijnen worden afgebeeld om te bewerkstelligen dat loxodromen (koerslijnen) als rechte lijnen zullen worden afgebeeld op de kaartprojectie.

Welnu, omdat een breedtecirkel op een noorderbreedte of zuiderbreedte φ slechts cos φ maal de omtrek van de evenaar heeft, moeten we dus op onze kaartprojectie op een noorderbreedte of zuiderbreedte φ een horizontale rekking met een factor 1/cos φ = sec φ toepassen ten opzichte van de schaal waarmee de evenaar wordt weergegeven om te bereiken dat de meridianen als verticale parallelle lijnen kunnen worden afgebeeld.

Maar omdat onze kaartprojectie ook nog hoekgetrouw moet zijn, moeten we dan bij onze kaartprojectie op een noorderbreedte of zuiderbreedte φ ook een verticale rekking met een factor 1/cos φ = sec φ toepassen ten opzichte van de schaal waarmee de evenaar wordt afgebeeld. En dat betekent dus dat we langs een meridiaan vanaf de evenaar naar elk van de beide polen toe niet alleen een oplopende horizontale rekking maar tevens een oplopende verticale rekking krijgen.

Hebben we nu een punt op aarde met een geografische lengte λ (positief voor oosterlengte, negatief voor westerlengte) en een geografische breedte φ (positief voor noorderbreedte, negatief voor zuiderbreedte), dan moeten we dit afbeelden op een punt met cartesische coördinaten (x;y) op onze kaartprojectie. Laten we omwille van de eenvoud aannemen dat we de evenaar laten samenvallen met de x-as en dat we de nulmeridiaan laten samenvallen met de y-as op onze kaartprojectie.

De x-coördinaat op onze kaart van een locatie op aarde met geografische coördinaten (λ;φ) is gemakkelijk te bepalen, want om verticale parallelle lijnen te verkrijgen voor de meridianen doen we op onze kaart net alsof alle breedtecirkels dezelfde omtrek hebben als de evenaar. Is de straal van de aarde R en drukken we λ uit in radialen dan is de werkelijke afstand van een punt op de evenaar tot de nulmeridiaan afgezien van het teken R∙λ.

Is nu de schaalfactor waarmee de evenaar op onze kaart wordt afgebeeld s₀ dan is de x-coördinaat op de kaart, en dus, afgezien van het teken, de horizontale afstand op de kaart tot de nulmeridiaan, gelijk aan:

(1) x = s₀∙R∙λ

Deze zelfde waarde houden we op onze kaart aan voor locaties die niet op de evenaar liggen, zodat meridianen worden afgebeeld als evenwijdige verticale lijnen en we als gevolg daarvan voor locaties met een geografische breedte φ op onze kaartprojectie een horizontale rekking met een factor 1/cos φ = sec φ krijgen.

De verticale afstand tot de evenaar die het punt met geografische coördinaten (λ;φ) op onze kaart moet krijgen is niet zo gemakkelijk te bepalen. De rekking langs een breedtecirkel is constant voor onze kaartprojectie, zodat x recht evenredig is met λ, en uit (1) volgt dan ook dat we hebben:

(2) dx/dλ = s₀∙R

De rekking langs een meridiaan is echter niet constant maar neemt toe in de richting van de beide polen zodat y niet recht evenredig is met φ. Op een geografische breedte φ hebben we een verticale (en horizontale) rekking met een factor 1/cos φ = sec φ ten opzichte van de schaal s₀ waarmee de equator wordt afgebeeld, zodat we ook kunnen zeggen dat we voor een geografische breedte φ een verticale (en horizontale) schaalfactor s_φ hebben waarvoor geldt:

(3) s_φ = s₀∙sec φ

Laten we nu ten noorden of ten zuiden van het punt met geografische coördinaten (λ;φ) een tweede punt (λ;φ + ∆φ) op aarde kiezen, dat dus op dezelfde meridiaan ligt. Op onze kaartprojectie krijgen deze locaties dan resp. de coördinaten (x;y) en (x;y+∆y). De onderlinge afstand van deze punten gemeten langs de meridiaan bedraagt dan (afgezien van het teken van het increment) R∙∆φ, maar hoe groot moet nu de verticale afstand ∆y van deze punten op onze kaart worden? Als de punten dicht bij elkaar liggen, en ∆φ dus dicht bij nul ligt, dan zal de verticale schaalfactor s_φ die geldt voor het punt met geografische coördinaten (λ;φ) niet noemenswaardig veranderen langs de meridiaan naar het punt (λ;φ + ∆φ), zodat dan moet gelden:

(4) ∆y ≈ s_φ∙R∙∆φ,

en dus ook:

(5) ∆y/∆φ ≈ s_φ∙R

Deze benadering wordt beter naarmate we ∆φ dichter tot nul laten naderen, zodat dus geldt:

(6) dy/dφ = s_φ∙R

en op grond van (3) dus ook:

(7) dy/dφ = s₀∙R∙sec φ

Nu beelden we de equator af op de x-as, zodat voor φ = 0 geldt y = 0, en dus volgt uit (7) dat:

(8) y = s₀∙R∙∫₀^φsec θ∙dθ

Vergelijk je nu (1) en (8), dan zie je dat voor de afbeelding van een punt met geografische coördinaten (λ;φ) bij de Mercatorprojectie geldt dat de verticale afstand tot de evenaar op de kaart zich verhoudt tot de horizontale afstand tot de nulmeridiaan op de kaart zoals ∫₀^φsec θ∙dθ zich (afgezien van het teken) verhoudt tot λ. En dus is het noodzakelijk deze integraal te evalueren om een Mercatorprojectie te kunnen realiseren. Voor -½π < φ < ½π geldt:

(9) ∫₀^φsec θ∙dθ = ln(tan(π/4 + φ/2))

[ Bericht 0% gewijzigd door Riparius op 14-06-2012 13:49:57 ]

Goed, ik snap het half. Pak zodirect de figuren erbij om je formules wat beter te begrijpen, kon je tot vrij ver volgen. Als ik het juist beredeneer je het verschil (dy/dφ), en om daarna tot de absolute afstand op de kaart te komen moet je dus de integraal nemen. Wikipedia stelt dat de Mercatorprojectie een cilinderprojectie is. Als ik het juist heb gelezen weerlegt Eli Maor dit in zijn boek, omdat de Mercatorprojectie eigenlijk geen directe projectie van een sfeer op een 2-dimensionaal vlak is, maar een soort 'wiskundige projectie'. Klopt dit? Ik las verkeerd, helder.

Tevens:


[ Bericht 3% gewijzigd door Muiroe op 14-06-2012 13:27:08 ]

quote:

Op donderdag 14 juni 2012 13:15 schreef Muiroe het volgende:
Tevens:
[ afbeelding ]

Ziet er keurig uit voor boeken van bijna 90 jaar oud, daar bof je maar mee (mijn exemplaar is een stuk minder).

quote:

Op donderdag 14 juni 2012 13:44 schreef Riparius het volgende:

[..]

Ziet er keurig uit voor boeken van bijna 90 jaar oud, daar bof je maar mee (mijn exemplaar is een stuk minder).

Het is wel 'professioneel gerestaureerd'. Het is uiteraard niet puntgaaf, maar enfin. En er is veel in de kantlijn geschreven met potlood. f(x) = f{a+(x-a)} dit soort dingen (Taylorreeks)

Ik denk dat je met φ de hoek tussen de straal van de aarde en de hoogte van het middelpunt van de aarde tot het middelpunt van een breedtecirkel bedoelt?

[ Bericht 10% gewijzigd door Muiroe op 14-06-2012 16:55:22 ]

Ik moet echt leren lezen

Goed, ik snap je tekst, op 2 kleine stukjes na.

(1): Bij de horizontale afstand krijg je omwille van de rek toch ook een vermenigvuldiging met sec(φ)?
En daarmee begrijp ik waarschijnlijk de vergelijking tussen (1) en (8) ook niet. (Ofwel het laatste stukje)

quote:

Op donderdag 14 juni 2012 17:08 schreef Muiroe het volgende:
Goed, ik snap je tekst, op 2 kleine stukjes na.

(1): Bij de horizontale afstand krijg je omwille van de rek toch ook een vermenigvuldiging met sec(φ)?

Jazeker, maar dat zit al verdisconteerd in formule (1). Als je een punt op aarde hebt met geografische coördinaten (λ;φ), dan heeft de breedtecirkel die door dat punt loopt een radius R∙cos φ, zodat de werkelijke afstand van dat punt op aarde tot de nulmeridiaan gemeten langs de breedtecirkel (afgezien van het teken) R∙cos φ∙λ bedraagt. Op de kaart zou dat dus een horizontale coördinaat x = s₀∙R∙cos φ∙λ opleveren als we de afbeelding niet in horizontale richting zouden rekken met een factor 1/cos φ = sec φ. Maar omdat we wel rekken in horizontale richting met een factor sec φ wordt de horizontale coördinaat dus x = s₀∙R∙cos φ∙λ∙sec φ = s₀∙R∙λ.

quote:

En daarmee begrijp ik waarschijnlijk de vergelijking tussen (1) en (8) ook niet. (Ofwel het laatste stukje)

Ik neem aan dat het nu wel duidelijk is.

Hallo,

Graag wil ik een vraagje stellen over de formule: y=a(x-p)^2+q

Mijn vraag is wat is x? Ik had al gegoogled maar ik kon het antwoord nog niet vinden. Alvast bedankt voor uw antwoord .

Groet,

superky

quote:

Op donderdag 14 juni 2012 19:11 schreef superky het volgende:
Hallo,

Graag wil ik een vraagje stellen over de formule: y=a(x-p)^2+q

Mijn vraag is wat is x? Ik had al gegoogled maar ik kon het antwoord nog niet vinden. Alvast bedankt voor uw antwoord .

Groet,

superky

x is een variabele, p wordt als een bekende constante beschouwd, evenals q.
Om x te kunnen berekenen hebben we wel wat meer informatie nodig. Het uitwerken van de haakjes levert op:
x² - 2px + p² + q

quote:

Op donderdag 14 juni 2012 19:20 schreef Muiroe het volgende:

[..]

x is een variabele, p wordt als een bekende constante beschouwd, evenals q.
Om x te kunnen berekenen hebben we wel wat meer informatie nodig. Het uitwerken van de haakjes levert op:
x² - 2px + p² + q

Dat wordt waarschijnlijk bedoeld, maar in principe kan y een functie zijn van p,q en/of x, zolang je dat niet aangeeft met haakjes.

quote:

Op donderdag 14 juni 2012 19:20 schreef Muiroe het volgende:

[..]

x is een variabele, p wordt als een bekende constante beschouwd, evenals q.
Om x te kunnen berekenen hebben we wel wat meer informatie nodig. Het uitwerken van de haakjes levert op:
x² - 2px + p² + q

Bepaal de functie van de parabool als de parabool de x-as snijdt voor x=0 en x=3
en als verder nog gegeven is dat de top op de lijn y=-7 ligt.

f(x)=...

quote:

Op donderdag 14 juni 2012 19:11 schreef superky het volgende:
Hallo,

Graag wil ik een vraagje stellen over de formule: y = a(x-p)²+q

Mijn vraag is wat is x? Ik had al gegoogled maar ik kon het antwoord nog niet vinden. Alvast bedankt voor uw antwoord .

Groet,

superky

Je vraag is strict genomen niet te beantwoorden, je formule geeft alleen aan hoe een grootheid y is gerelateerd aan de grootheden a, p, q en x. Maar doorgaans worden x en y voor variabelen of onbekende grootheden gebruikt en letters als a, p en q voor constanten of bekende grootheden. In een cartesisch assenstelsel met een x-as en een y-as stelt deze formule voor a ongelijk aan nul de vergelijking voor van een parabool met als top het punt met de coördinaten (p;q). Als a > 0 dan is het een dalparabool en als a < 0 een bergparabool. Begrijp je dit?

[ Bericht 0% gewijzigd door Riparius op 14-06-2012 19:38:25 ]

quote:

Op donderdag 14 juni 2012 19:26 schreef superky het volgende:

[..]

Bepaal het functievoorschrift van de parabool als de parabool de x-as snijdt voor x=0 en x=3
en als verder nog gegeven is dat de top op de lijn y=-7 ligt.

f(x)=...

Bedenk eerst eens dat de snijpunten van de parabool met de x-as symmetrisch liggen t.o.v. de (verticale) symmetrie-as van de parabool, en dat de top van de parabool op de symmetrie-as ligt. Wat zijn dus de coördinaten van de top van de parabool?

quote:

Op donderdag 14 juni 2012 19:37 schreef Riparius het volgende:

[..]

Bedenk eerst eens dat de snijpunten van de parabool met de x-as symmetrisch liggen t.o.v. de (verticale) symmetrie-as van de parabool, en dat de top van de parabool op de symmetrie-as ligt. Wat zijn dus de coördinaten van de top van de parabool?

(3/2, -7)

quote:

Op donderdag 14 juni 2012 19:44 schreef superky het volgende:

[..]

(3/2, -7)

Dat is correct. Het functievoorschrift waarvan de grafiek een parabool is met top (p;q) is in het algemeen:

f(x) = a(x - p)² + q

Nu weten we al dat p = 3/2 en q = -7, dus hebben we:

f(x) = a(x - 3/2)² - 7

Nu moeten we de waarde van a nog bepalen. Je weet dat x = 0 en x = 3 de nulpunten zijn van deze functie, dus f(0) = f(3) = 0. Als je dus (bijvoorbeeld) x = 0 invult in het functievoorschift dat we nu hebben, dan moet de uitkomst nul zijn. Gebruik dit om de waarde van a te bepalen.

Maar uiteraard wil ik Riparius nog even bedanken voor zijn tijd in het steken van een uitmuntende post over de Mercatorprojectie. Het is me in ieder geval duidelijk! Onwaarschijnlijk dat ik wiskunde wil gaan studeren nadat ik in klas 2 niets eens begreep dat bij een lineaire vergelijking y = ax+b dat bij x stapjes naar rechts je a stapjes omhoog gaat. (5 voor het proefwerk, na herkansing een 10)

quote:

Op donderdag 14 juni 2012 19:49 schreef Riparius het volgende:

[..]

Dat is correct. Het functievoorschrift waarvan de grafiek een parabool is met top (p;q) is in het algemeen:

f(x) = a(x - p)² + q

Nu weten we al dat p = 3/2 en q = -7, dus hebben we:

f(x) = a(x - 3/2)² - 7

Nu moeten we de waarde van a nog bepalen. Je weet dat x = 0 en x = 3 de nulpunten zijn van deze functie, dus f(0) = f(3) = 0. Als je dus (bijvoorbeeld) x = 0 invult in het functievoorschift dat we nu hebben, dan moet de uitkomst nul zijn. Gebruik dit om de waarde van a te bepalen.

Hoi, sorry dat ik nu een beetje laat reageer maar a=63/4

quote:

Op donderdag 14 juni 2012 21:53 schreef Amoeba het volgende:

met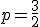








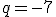
Misschien moet je je berekening eens bekijken.

Je moet weten dat: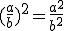

Thanks je hebt het correct.

Nu wil ik graag een andere kleine vraagje stellen: stel de kwadratische functie op van de grafiek die door het punt (2,-1) gaat en een top/dal heeft bij (5,3).

Als antwoord heb ik:



Maar het juiste antwoord is:


Mijn vraag is hoe kom je aan het goede antwoord ? Overigen heb ik gemerkt dat ik hem bijna goed had, maar dat ik ergens een foutje heb gemaakt. En dat zit ik dus nog te zoeken. Graag wacht ik op uw reactie. Alvast bedankt voor uw antwoord.

Vul maar eens x=2 in in je eigen antwoord, dat gaat duidelijk niet goed.

Je wil dat f(2) = -1. Je weet dat f(x) = a(x-5)^2 + 3. Los dan a op uit f(2)=-1.

Ik laat jullie ook mijn berekeningen zien dan is het duidelijk wat ik heb gedaan.



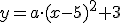
Door het punt (2,-1)

quote:

Op zaterdag 16 juni 2012 11:11 schreef superky het volgende:
Ik laat jullie ook mijn berekeningen zien dan is het duidelijk wat ik heb gedaan.



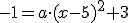
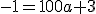
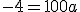
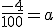
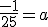
Door het punt (2,-1)

Ik heb geen idee hoe je aan die 100a komt, maar als je zowel de x als de y invult krijg je dit: