SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Hah, ik had het even snel uit mijn hoofd opschreven, stom dat ik het niet zag.quote:Op maandag 4 juni 2012 18:12 schreef Riparius het volgende:
[..]
Heel eenvoudig: als je een rechthoekige driehoek hebt met een hoek van 60 graden, dan is de andere scherpe hoek 30 graden. En uiteraard is de cosinus van een hoek de sinus van het complement, daarom heet het ook een cosinus (als afkorting van complementi sinus).
Hoe kom je bij die a=b/(b-1)? Ik weet niets over hyperbolen verder.quote:
[..]
Ja, je moet het stelsel
a^2+b^2 = 16
a=b/(b-1)
oplossen.
Ik noem de gezochte x-coördinaat a, en de gezochte y-coördinaat b. Dan geldt dat ab/2 de oppervlakte is van de driehoek ingesloten door de x en y as en de gezochte lijn. Maar de oppervlakte is ook op een andere manier uit te drukken, namelijk: (a-1)(b-1)/2 + 1.quote:Op maandag 4 juni 2012 20:26 schreef Amoeba het volgende:
[..]
Hoe kom je bij die a=b/(b-1)? Ik weet niets over hyperbolen verder.
Dus (a-1)(b-1)/2 + 1 = ab/2. En dan oplossen voor a geeft a=b/(b-1).
Kun je dit toelichten?quote:
[..]
Ik noem de gezochte x-coördinaat a, en de gezochte y-coördinaat b. Dan geldt dat ab/2 de oppervlakte is van de driehoek ingesloten door de x en y as en de gezochte lijn. Maar de oppervlakte is ook op een andere manier uit te drukken, namelijk: (a-1)(b-1)/2 + 1.
Dus (a-1)(b-1)/2 + 1 = ab/2. En dan oplossen voor a geeft a=b/(b-1).
Dat is inderdaad het idee, maar mijn algebra klopt niet.quote:
Gewoon de driehoek splitsen in een vierkant en twee kleine driehoeken.
Krijg je die onzin a = ab-b
a = b(a-1)
a/(a-1) = b
zo kan het ook?
[ Bericht 55% gewijzigd door #ANONIEM op 04-06-2012 20:44:44 ]
a = b(a-1)
a/(a-1) = b
zo kan het ook?
[ Bericht 55% gewijzigd door #ANONIEM op 04-06-2012 20:44:44 ]
En dit geeftquote:
(a+b)/2 = ab/2
a+b = ab
b/a=b
Crap, ik kan niet meer helder denken
Dit gaat iig nergens heen.
26"
Fading slowly.
Fading slowly.
Je laatste regel klopt niet.quote:Op maandag 4 juni 2012 20:43 schreef Unsub het volgende:
[..]
En dit geeft
(a+b)/2 = ab/2
a+b = ab
b/a=b
Crap, ik kan niet meer helder denken
Dit gaat iig nergens heen.
Ik denk dat je zoiets moet doen.
a + b = ab
kwadrateren geeft
a² + b² + 2ab = a²b²
We weten
a²+b²=16
dus
16 + 2ab = a²b²
Substitueer ab=x. Dan krijgen we een kwadratische vergelijking in x:
x² - 2x - 16 = 0.
Met de ABC-formule kunnen we dan x oplossen. We weten dan dus de waarde van ab, want ab=x en x is bekend. Dus a=x/b. Maar omdat ook a+b=x, hebben we ook a=x-b. Dus x-b = x/b. Dus bx - b² = x. Dus dan hebben we een kwadratische vergelijking in b. Die kan je ook weer oplossen. Dan heb je dus b, en dan kan je ook a berekenen.
(De details laat ik over aan amoeba
)
a + b = ab
kwadrateren geeft
a² + b² + 2ab = a²b²
We weten
a²+b²=16
dus
16 + 2ab = a²b²
Substitueer ab=x. Dan krijgen we een kwadratische vergelijking in x:
x² - 2x - 16 = 0.
Met de ABC-formule kunnen we dan x oplossen. We weten dan dus de waarde van ab, want ab=x en x is bekend. Dus a=x/b. Maar omdat ook a+b=x, hebben we ook a=x-b. Dus x-b = x/b. Dus bx - b² = x. Dus dan hebben we een kwadratische vergelijking in b. Die kan je ook weer oplossen. Dan heb je dus b, en dan kan je ook a berekenen.
(De details laat ik over aan amoeba
)
Die hebben we dus nu:quote:
Het lijkt me dat het maken van de juiste vierdegraadsvergelijking niet het grootste probleem is.
a2 + b2 = 16
-a4 + 2a3 + 14a2 -32a + 16 = 0.
Ik heb morgen een proefwerk. Alleen ik snap niks van de discriminant.
Ik heb een som waar ik maar niet uit kan komen :S
f (x) = 2x² -4x & g(x) = x + 10.
En dan moet je ook nog afleiden of die de lijn snijdt, raakt of geen gemeenschappelijk punt heeft.
Wie o wie kan me helpen?
Alvast bedankt
Ik heb een som waar ik maar niet uit kan komen :S
f (x) = 2x² -4x & g(x) = x + 10.
En dan moet je ook nog afleiden of die de lijn snijdt, raakt of geen gemeenschappelijk punt heeft.
Wie o wie kan me helpen?
Alvast bedankt
Stel f(x) = g(x) en los op voor x met behulp van de abc-formule.quote:
Ik heb morgen een proefwerk. Alleen ik snap niks van de discriminant.
Ik heb een som waar ik maar niet uit kan komen :S
f (x) = 2x² -4x & g(x) = x + 10.
En dan moet je ook nog afleiden of die de lijn snijdt, raakt of geen gemeenschappelijk punt heeft.
Wie o wie kan me helpen?
Alvast bedankt
De discriminant is inderdaad 105. Laat maar zien hoe jij het berekent.quote:
thenxero.
ik heb het uitgerekend en kom op 55 uit maar in het antwoordenboekje staat 105.
Een lijn snijdt wanneer geldt:
f(x) = g(x) & f'(x)*g'(x) = -1
Een lijn raakt wanneer:
f(x) = g(x) & f'(x) = g'(x)
f(x) = g(x) & f'(x)*g'(x) = -1
Een lijn raakt wanneer:
f(x) = g(x) & f'(x) = g'(x)
Sorry. b = (-1-√17 +/- √(14-2√17))/2quote:
Amoeba, heb je b al berekend van het Riparius probleem?
ofzo?
Over die lijn door (1,1):
noem de hoek tussen de lijn en de x-as θ, noem x=cosθ en y=sinθ, dan moet
,
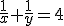dus
,
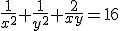dus
,
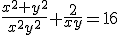dus
,
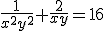dus
,
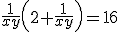substitutie z=1/(xy),
,
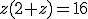geeft een oplossing p voor z en dus ook voor xy.
Vervolgens x=1/(yp) substitueren in
,
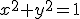geeft
,
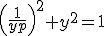dus
,
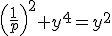substitutie z=y^2,
,
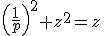geeft een oplossing q voor y,
vervolgens met Pythagoras het antwoord berekenen.
noem de hoek tussen de lijn en de x-as θ, noem x=cosθ en y=sinθ, dan moet
dus
dus
dus
dus
substitutie z=1/(xy),
geeft een oplossing p voor z en dus ook voor xy.
Vervolgens x=1/(yp) substitueren in
geeft
dus
substitutie z=y^2,
geeft een oplossing q voor y,
vervolgens met Pythagoras het antwoord berekenen.
b = (1+√17 +/- √(14-2√17))/2 krijg ik.quote:
[..]
Sorry. b = (-1-√17 +/- √(14-2√17))/2
ofzo?
Volgens mij hebben we dan
b = (1+√17 + √(14-2√17))/2
a = (1+√17 - √(14-2√17))/2
(want het probleem is symmetrisch in a en b en het was gegeven dat a<b)
-bx, mijn excuses. Je hebt gelijk.quote:
[..]
b = (1+√17 +/- √(14-2√17))/2 krijg ik.
Volgens mij hebben we dan
b = (1+√17 + √(14-2√17))/2
a = (1+√17 - √(14-2√17))/2
(want het probleem is symmetrisch in a en b en het was gegeven dat a<b)
Numeriek lijkt het ook allemaal te kloppen zo in wolfram alpha. Volgens mij is dit hem dus. Leuk probleempje.quote:
Waar ellipsen een mens wel niet toe brengen.quote:Op maandag 4 juni 2012 21:19 schreef thenxero het volgende:
[..]
Numeriek lijkt het ook allemaal te kloppen zo in wolfram alpha. Volgens mij is dit hem dus. Leuk probleempje.
Haha. Nu is het eigenlijk mijn beurt om eens een leuk probleempje te posten.quote:
[..]
Waar ellipsen een mens wel niet toe brengen.
Ik kwam laatst nog wat leuks tegen voor hier, maar nu weet ik het niet meer
En dat is volkomen correct, waarbij dus A(a;0) het snijpunt is met de x-as en B(0;b) het snijpunt met de y-as.quote:
[..]
b = (1+√17 +/- √(14-2√17))/2 krijg ik.
Volgens mij hebben we dan
b = (1+√17 + √(14-2√17))/2
a = (1+√17 - √(14-2√17))/2
(want het probleem is symmetrisch in a en b en het was gegeven dat a<b)
Prima gedaan, de clou is natuurlijk om niet te verzanden in een vierdegraadsvergelijking die je niet gemakkelijk op kunt lossen.
Ik zag jou er nog wel voor aan om een opgave te geven waarbij je een vierdegraadsvergelijking moet oplossen, gezien je vorige opgavequote:
[..]
En dat is volkomen correct, waarbij dus A(a;0) het snijpunt is met de x-as en B(0;b) het snijpunt met de y-as.
Prima gedaan, de clou is natuurlijk om niet te verzanden in een vierdegraadsvergelijking die je niet gemakkelijk op kunt lossen.
.
Noem je dit wel gemakkelijk dan.quote:
[..]
En dat is volkomen correct, waarbij dus A(a;0) het snijpunt is met de x-as en B(0;b) het snijpunt met de y-as.
Prima gedaan, de clou is natuurlijk om niet te verzanden in een vierdegraadsvergelijking die je niet gemakkelijk op kunt lossen.
Ik wed dat 90% van alle havo leerlingen hier de steek zouden laten vallen zodra je NOG een keer met de ABC formule aan de haal moet wanneer er al zo'n harde vergelijking x = 1+√17 staat.
Die vorige opgave was bijzonder pittig inderdaad. Kopbrekens, tot middenin de nacht.quote:
[..]
Ik zag jou er nog wel voor aan om een opgave te geven waarbij je een vierdegraadsvergelijking moet oplossen, gezien je vorige opgave
Vanuit het perspectief van een wiskundige is dit natuurlijk de meest elementaire wiskunde die er bestaat.quote:
[..]
Noem je dit wel gemakkelijk dan.
Ik wed dat 90% van alle havo leerlingen hier de steek zouden laten vallen zodra je NOG een keer met de ABC formule aan de haal moet wanneer er al zo'n harde vergelijking x = 1+√17 staat.
Geweldig.quote:
[..]
Vanuit het perspectief van een wiskundige is dit natuurlijk de meest elementaire wiskunde die er bestaat.
Ik heb trouwens geen rekenmachine in m'n hand gehad. Toen jij zei of ik b al had opgelost had ik slechts de discriminant op papier staan, stom dat ik er blind vanuit ging dat er huppeldepup + bx + pupdehuppel zou staan
Amoeba en andere liefhebbers, aanschouw het volgende probleem.
Bepaal het aantal getallen tussen de 1000 en de 9999, zodat alle vier cijfers verschillen en ongelijk aan nul zijn.
Bepaal het aantal getallen tussen de 1000 en de 9999, zodat alle vier cijfers verschillen en ongelijk aan nul zijn.
Dit riekt naar een vorm van statistiek/kansrekening (Aldus behandeld in wiskunde D) ofzo.quote:Op maandag 4 juni 2012 21:28 schreef thenxero het volgende:
Amoeba en andere liefhebbers, aanschouw het volgende probleem.
Bepaal het aantal getallen tussen de 1000 en de 9999, zodat alle vier cijfers verschillen en ongelijk aan nul zijn.
[ Bericht 3% gewijzigd door #ANONIEM op 04-06-2012 21:31:23 ]
Het heeft niks met kansrekening te maken, het is elementaire combinatoriek. Veel middelbare scholieren halen dat door elkaarquote:
[..]
Dit riekt naar een vorm van kansrekening ofzo.
.Maar je hebt geen voorkennis nodig om dit te kunnen oplossen. De oplossing is erg eenvoudig (als je erop komt).
