[Bèta wiskunde] Huiswerk- en vragentopic

zondag 13 mei 2012 @ 14:40:49 #102

thenxero

quote:
Op zondag 13 mei 2012 14:28 schreef Amoeba het volgende:

[..]

[ afbeelding ]

?

Je moet geen { } haken gebruiken. Daardoor gaat wolframalhpa de mist in.

Je begin en eindwaardes van k kloppen niet. Waarom heb je die zo gekozen?

zondag 13 mei 2012 @ 14:41:50 #103

PizzaGeit

quote:
Op zondag 13 mei 2012 14:37 schreef thenxero het volgende:

[..]

Nee, als je dit had gezegd was het wel goed geweest:
$\frac{\sin x}{n} = ?$
$six=?$
$?=6$

Volgende keer beter

zondag 13 mei 2012 @ 14:44:05 #104

PizzaGeit

Dit is dan ook weer niet goed zeker

zondag 13 mei 2012 @ 14:44:10 #105

#ANONIEM

[tex]

quote:
Op zondag 13 mei 2012 14:40 schreef thenxero het volgende:

[..]

Je moet geen { } haken gebruiken. Daardoor gaat wolframalhpa de mist in.

Je begin en eindwaardes van k kloppen niet. Waarom heb je die zo gekozen?

Omdat ik het interval van 2 tot 24 wilde..

Xk klopt wel?

zondag 13 mei 2012 @ 14:50:07 #106

thenxero

quote:
Op zondag 13 mei 2012 14:44 schreef PizzaGeit het volgende:
[ afbeelding ]

Dit is dan ook weer niet goed zeker

Ziet er prima uit hoor.

quote:
Op zondag 13 mei 2012 14:44 schreef Amoeba het volgende:
[tex]

[..]

Omdat ik het interval van 2 tot 24 wilde..

Xk klopt wel?

Als je sommeert van k=2 tot k=24, dan is dus je het eerste midden van de deelintervalletjes bij 2+0.5*2 = 3, en de laatste bij 2+0.5*24 = 14. Je "integreert" dus eigenlijk van 2.75 tot 14.25 op deze manier.

zondag 13 mei 2012 @ 14:58:16 #107

#ANONIEM

Ah, oke.

Xk = X_beginwaarde +stapgrootte*k
a en b zou ik dan zo uit moeten drukken dat de Xk * k = a (die waarde van k dus), evenals voor b?

Zit ik zo goed?

zondag 13 mei 2012 @ 15:04:46 #108

thenxero

Zoiets...

x_k = linkergrens + (de helft van de stapgrootte) + (stapgrootte * k)

En dan sommeren van k=0 tot k zodanig dat x_k = (rechtergrens - de helft van de stapgrootte).

Of anders gezegd: Als linkergrens a heet, en rechtergrens b, dan laat je k zo lopen dat je (b-a)/(stapgrootte) termen krijgt.

zondag 13 mei 2012 @ 15:07:33 #109

#ANONIEM

[tex]\sum_{k=30}^{70} (3(2+1/10k)-2(2+1/10k)^2) \cdot 1/10[/tex]

Stel dat ik wil gaan van x=5 tot x=10
Functie: 3x - 2x^2
Stapgrootte: 1/10

Dan is dit fout. Laat het me nogmaals proberen..

[ Bericht 43% gewijzigd door #ANONIEM op 13-05-2012 15:09:18 ]

zondag 13 mei 2012 @ 15:11:17 #110

#ANONIEM

$\sum_{k=0}^{50} (3(2,05+1/10k)-2(2,05+1/10k)^2) \cdot 1/10$

Stel dat ik wil gaan van x=5 tot x=10
Functie: 3x - 2x^2
Stapgrootte: 1/10

Zo?

zondag 13 mei 2012 @ 15:14:07 #111

#ANONIEM

Maar het komt absoluut niet overeen met de integraal...

zondag 13 mei 2012 @ 15:15:06 #112

thenxero

Integreer eens van 2 tot 7.1, en kijk wat er gebeurt

zondag 13 mei 2012 @ 15:18:29 #113

#ANONIEM

Maar die onderste, moet die in dit geval 0 zijn? Of iets van 30?

Edit: Ik heb die integraal bekeken.

Moet k van 30 tot 80 lopen?

[ Bericht 40% gewijzigd door #ANONIEM op 13-05-2012 15:21:05 ]

zondag 13 mei 2012 @ 15:22:37 #114

thenxero

Dan is je beginwaarde 5.05 (OK) en je eindwaarde 10.05 (niet OK), het laatste midden van je rechthoek zit bij 9.95

zondag 13 mei 2012 @ 15:23:17 #115

#ANONIEM

Dan 79.

zondag 13 mei 2012 @ 15:24:29 #116

thenxero

Inderdaad. Je had ook gewoon x_k = 5.05 + k/10 kunnen nemen, en dan sommeren van k=0 tot k=49 . Maar dat komt op hetzelfde neer.

Komt het nu wel mooi overeen met de integraal?

zondag 13 mei 2012 @ 15:24:31 #117

#ANONIEM

$\sum_{k=30}^{79} (3(2,05+1/10k)-2(2,05+1/10k)^2) \cdot 1/10$

zondag 13 mei 2012 @ 15:25:51 #118

#ANONIEM

Ohja, ik zie nu pas dat ik dat had moeten doen, aangezien ik net de hele tijd vanaf x=2 nam etc.

Maargoed, dan geldt dus dit:

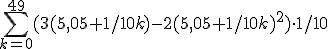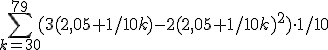
$\sum_{k=0}^{49} (3(5,05+1/10k)-2(5,05+1/10k)^2) \cdot 1/10$ = $\sum_{k=30}^{79} (3(2,05+1/10k)-2(2,05+1/10k)^2) \cdot 1/10$

zondag 13 mei 2012 @ 15:29:41 #119

thenxero

Precies. Kies je favoriete som

. Wat komt eruit? En wat komt er uit de integraal?

zondag 13 mei 2012 @ 15:35:27 #120

#ANONIEM

-470,825 bij de somrij
-470,833 bij de integraal.

Hoe lost je GR eigenlijk een integraal op, een somrij toch gewoon?
Mijn primitieve komt uit op -2025/6 Hetzelfde als de integraal dus.

zondag 13 mei 2012 @ 15:39:21 #121

thenxero

Nice!

Ik weet niet hoe je GR het doet. Er zijn wel methodes die nauwkeuriger en sneller werken dan Riemannsommen. Kijk eens op http://en.wikipedia.org/wiki/Numerical_integration bijvoorbeeld. In plaats van met rechthoeken kan je met trapeziumpjes werken.

zondag 13 mei 2012 @ 15:47:53 #122

#ANONIEM

Genoeg tijd op het centraal examen, 3.5 uur voor Wiskunde B. Harstikke bedankt.

zondag 13 mei 2012 @ 15:48:56 #123

dramatic

quote:
Op zondag 13 mei 2012 15:47 schreef Amoeba het volgende:
Genoeg tijd op het centraal examen, 3.5 uur voor Wiskunde B. Harstikke bedankt.

Ik toch echt maar 3.0.. Maar dat heeft vast weer met staatsexamen te maken.

zondag 13 mei 2012 @ 15:49:16 #124

kutkloon7

quote:
Op zondag 13 mei 2012 15:35 schreef Amoeba het volgende:
-470,825 bij de somrij
-470,833 bij de integraal.

Hoe lost je GR eigenlijk een integraal op, een somrij toch gewoon?
Mijn primitieve komt uit op -2025/6 Hetzelfde als de integraal dus.

Ik dacht het wel, want ik meen me te herinneren dat de GR soms niet het precieze antwoord gaf bij het controleren van een integraal (dus dat de GR bijvoorbeeld 1.0001 als antwoord gaf terwijl het gewoon 1 moest zijn). Daarnaast is er dacht ik ook geen analytische methode die voor elke integraal werkt (want er bestaat niet altijd een integraal).
Succes met je examen!

zondag 13 mei 2012 @ 15:54:57 #125

kutkloon7

Ik vroeg me af of het ook mogelijk is sommige kwadratische recurrentievergelijkingen op te lossen. Als je een 'normale' lineaire recurrente betrekking
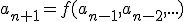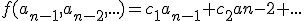$a_{n+1}=f(a_{n-1},a_{n-2},...)$ (waar f dan een lineaire functie is, dus $f(a_{n-1},a_{n-2},...)=c_1a_{n-1}+c_2a{n-2}+...$ )
hebt, kan je die oplossen door f te schrijven als een matrix (met een bepaalde beginvector) en de eigenvectoren te zoeken en de beginvector in die eigenvectoren uit te drukken, of door een genererende functie te zoeken.

Maar iets in de trant van
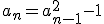
$a_n=a_{n-1}^2-1$
lijkt me niet op te lossen voor een willkeurige a₀.
Voor
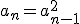
$a_n=a_{n-1}^2$
geldt wel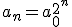 $a_n=a_{0}^{2^n}$
Maar het lukt me ook niet echt om dit op een systematische manier aan te tonen.
(Je kan wel in het algemeen stellen dat je een functie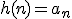 $h(n)=a_n$ zoekt waarvoor geldt
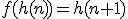$f(h(n))=h(n+1)$ , als
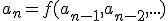$a_n=f(a_{n-1},a_{n-2},...)$ je recurrente betrekking is)

zondag 13 mei 2012 @ 15:59:19 #126

thenxero

Heb je al de methode geprobeerd met karakteristieke polynoom, particuliere oplossing, etc? (komt op hetzelfde neer als genererende functies, maar dan sneller)

zondag 13 mei 2012 @ 17:11:22 #127

#ANONIEM

quote:
Op zondag 13 mei 2012 15:48 schreef dramatic het volgende:

[..]

Ik toch echt maar 3.0.. Maar dat heeft vast weer met staatsexamen te maken.

Speciaal onderwijs. Ieder examen een half uur langer!

zondag 13 mei 2012 @ 17:29:39 #128

Riparius

quote:
Op zondag 13 mei 2012 15:49 schreef kutkloon7 het volgende:

[..]

Ik dacht het wel, want ik meen me te herinneren dat de GR soms niet het precieze antwoord gaf bij het controleren van een integraal (dus dat de GR bijvoorbeeld 1.0001 als antwoord gaf terwijl het gewoon 1 moest zijn). Daarnaast is er dacht ik ook geen analytische methode die voor elke integraal werkt (want er bestaat niet altijd een integraal).

Je bedoelt dat een primitieve niet altijd in elementaire functies is uit te drukken, dat is iets anders dan beweren dat er geen primitieve is.

Overigens denk ik dat een doodgewone GR wellicht altijd numerieke methoden gebruikt voor het evalueren van definiete integralen. Wat WolframAlpha doet is een stuk geavanceerder, want die weet ook voor sommige oneigenlijke integralen en integralen waarbij een primitieve niet in elementaire functies is uit te drukken toch het exacte antwoord te produceren. Vaak komt dat antwoord dan ietsje later pas op je scherm, namelijk nadat er al een numeriek antwoord is verschenen. Dat duidt erop dat WolframAlpha gebruik maakt van een bibliotheek met 'bekende' integralen die exact zijn te evalueren ook als een primitieve niet in elementaire functies is uit te drukken.

Probeer eens wat je GR hiervan bakt:

∫₀¹ ln(x)/(x-1)dx

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

zondag 13 mei 2012 @ 17:51:14 #129

thenxero

quote:
Op zondag 13 mei 2012 17:29 schreef Riparius het volgende:

[..]

Je bedoelt dat een primitieve niet altijd in elementaire functies is uit te drukken, dat is iets anders dan beweren dat er geen primitieve is.

Overigens denk ik dat een doodgewone GR wellicht altijd numerieke methoden gebruikt voor het evalueren van definiete integralen. Wat WolframAlpha doet is een stuk geavanceerder, want die weet ook voor sommige oneigenlijke integralen en integralen waarbij een primitieve niet in elementaire functies is uit te drukken toch het exacte antwoord te produceren. Vaak komt dat antwoord dan ietsje later pas op je scherm, namelijk nadat er al een numeriek antwoord is verschenen. Dat duidt erop dat WolframAlpha gebruik maakt van een bibliotheek met 'bekende' integralen die exact zijn te evalueren ook als een primitieve niet in elementaire functies is uit te drukken.

Probeer eens wat je GR hiervan bakt:

∫₀¹ ln(x)/(x-1)dx

Er hoort pi²/6 uit te komen, maar de GR geeft wel wat anders: 1.644828 ipv 1.64493. Komt inderdaad doordat de GR het altijd numeriek doet.

zondag 13 mei 2012 @ 17:52:08 #130

#ANONIEM

quote:
Op zondag 13 mei 2012 17:29 schreef Riparius het volgende:

[..]

Je bedoelt dat een primitieve niet altijd in elementaire functies is uit te drukken, dat is iets anders dan beweren dat er geen primitieve is.

Overigens denk ik dat een doodgewone GR wellicht altijd numerieke methoden gebruikt voor het evalueren van definiete integralen. Wat WolframAlpha doet is een stuk geavanceerder, want die weet ook voor sommige oneigenlijke integralen en integralen waarbij een primitieve niet in elementaire functies is uit te drukken toch het exacte antwoord te produceren. Vaak komt dat antwoord dan ietsje later pas op je scherm, namelijk nadat er al een numeriek antwoord is verschenen. Dat duidt erop dat WolframAlpha gebruik maakt van een bibliotheek met 'bekende' integralen die exact zijn te evalueren ook als een primitieve niet in elementaire functies is uit te drukken.

Probeer eens wat je GR hiervan bakt:

∫₀¹ ln(x)/(x-1)dx

Is deze met behulp van partieël integreren algebraïsch te doen?

zondag 13 mei 2012 @ 17:57:16 #131

Riparius

quote:
Op zondag 13 mei 2012 17:52 schreef Amoeba het volgende:

[..]

Is deze met behulp van partieël integreren algebraïsch te doen?

Nee.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

zondag 13 mei 2012 @ 17:57:47 #132

kutkloon7

quote:
Op zondag 13 mei 2012 17:29 schreef Riparius het volgende:

[..]

Je bedoelt dat een primitieve niet altijd in elementaire functies is uit te drukken, dat is iets anders dan beweren dat er geen primitieve is.

Uhuh, dat bedoel ik inderdaad (hoewel er natuurlijk ook functies zonder primitieve zijn, maar dat is weer een ander verhaal want die zijn dan niet continu).

zondag 13 mei 2012 @ 18:01:17 #133

kutkloon7

quote:
Op zondag 13 mei 2012 15:59 schreef thenxero het volgende:
Heb je al de methode geprobeerd met karakteristieke polynoom, particuliere oplossing, etc? (komt op hetzelfde neer als genererende functies, maar dan sneller)

Bedoel je de karakteristieke polynoom van een matrix?
Ik zou niet weten hoe dat werkt, bij een kwadratische functie.

zondag 13 mei 2012 @ 18:06:20 #134

thenxero

quote:
Op zondag 13 mei 2012 18:01 schreef kutkloon7 het volgende:

[..]

Bedoel je de karakteristieke polynoom van een matrix?
Ik zou niet weten hoe dat werkt, bij een kwadratische functie.

Je hebt gelijk, dat werkt alleen bij lineaire recurrente betrekkingen. Het enige wat ik zou kunnen bedenken is wat proberen met een genererende functie... misschien komt er wat moois uit maar misschien ook niet.

Je hebt een beetje hetzelfde probleem als bij differentiaalvergelijkingen: vaak is er gewoon geen analytische oplossing.

zondag 13 mei 2012 @ 20:47:42 #135

Uchiha1911

Snel vraagje: wat is de primitieve van 3^2x?
De afgeleide hiervan is 3^2x x ln(3) x 2 (doordifferentiëren), maar uit de primitieve kom ik niet. Hier is ook een regel voor lijkt me?

zondag 13 mei 2012 @ 21:20:51 #136

VanishedEntity

Simpel: 1/(ln3) * 1/2 * 3^2x . Gewoon goed kijken voor welke factoren je moet compenseren; hier moet je rekening houden met de factor 2 vanwege de 2 in de exponent èn de factor ln(3) vanwege het feit dat de afgeleide van a^x = ln(a) * a^x.

zondag 13 mei 2012 @ 22:13:18 #137

Riparius

quote:
Op zondag 13 mei 2012 20:47 schreef Uchiha1911 het volgende:
Snel vraagje: wat is de primitieve van 3^2x?
De afgeleide hiervan is 3^2x x ln(3) x 2 (door differentiëren), maar uit de primitieve kom ik niet. Hier is ook een regel voor lijkt me?

Je zou kunnen beginnen met te bedenken dat:

3^2x = (3²)^x = 9^x

Het is dus gewoon een exponentiële functie, en aangezien 9 = e^{ln 9} heb je dus:

3^2x = 9^x = (e^{ln 9})^x = e^{x∙ln 9}

Nu zou het je geen moeite meer mogen kosten hiervan een primitieve op te schrijven.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

maandag 14 mei 2012 @ 09:05:35 #138

Uchiha1911

quote:
Op zondag 13 mei 2012 22:13 schreef Riparius het volgende:

[..]

Je zou kunnen beginnen met te bedenken dat:

3^2x = (3²)^x = 9^x

Het is dus gewoon een exponentiële functie, en aangezien 9 = e^{ln 9} heb je dus:

3^2x = 9^x = (e^{ln 9})^x = e^{x∙ln 9}

Nu zou het je geen moeite meer mogen kosten hiervan een primitieve op te schrijven.

Hartstikke bedankt! Dat zou betekenen dat het 1/ln(9) x e^x wordt?

maandag 14 mei 2012 @ 09:51:30 #139

Riparius

quote:
Op maandag 14 mei 2012 09:05 schreef Uchiha1911 het volgende:

[..]

Hartstikke bedankt! Dat zou betekenen dat het 1/ln(9) ∙ e^x wordt?

Nee, een primitieve van e^{x∙ln 9} is 1/ln(9)∙e^{x∙ln 9}.

Gebruik alleen geen letter x als teken voor vermenigvuldiging, en zeker niet als je x ook nog als variabele gebruikt.

Verder kun je natuurlijk altijd WolframAlpha gebruiken om de afgeleide te bepalen en zo te controleren of je primitieve wel juist is.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

maandag 14 mei 2012 @ 14:35:46 #140

kutkloon7

quote:
Op zondag 13 mei 2012 18:06 schreef thenxero het volgende:

[..]

Je hebt gelijk, dat werkt alleen bij lineaire recurrente betrekkingen. Het enige wat ik zou kunnen bedenken is wat proberen met een genererende functie... misschien komt er wat moois uit maar misschien ook niet.

Je hebt een beetje hetzelfde probleem als bij differentiaalvergelijkingen: vaak is er gewoon geen analytische oplossing.

Ok, dank! Ik hoopte dat er misschien een bekende methode was om dit soort recurrente betrekkingen op te lossen, maar ik dacht al dat veel niet-lineaire recurrente betrekkingen niet echt 'op te lossen' zijn.

maandag 14 mei 2012 @ 18:25:25 #141

thabit

quote:
Op maandag 14 mei 2012 14:35 schreef kutkloon7 het volgende:

[..]

Ok, dank! Ik hoopte dat er misschien een bekende methode was om dit soort recurrente betrekkingen op te lossen, maar ik dacht al dat veel niet-lineaire recurrente betrekkingen niet echt 'op te lossen' zijn.

Is in het algemeen niet te doen, alleen in speciale gevallen. Dit soort kwadratische recursies spelen zelfs een belangrijke rol in de chaostheorie. Je kunt er ook fractals mee maken, zoals de Mandelbrotverzameling.

Een voorbeeld van eentje die nog wel te doen is (ik verklap de oplossing nog niet):
a₁ = 1/3, a_n+1 = 2a_n² - 1.

maandag 14 mei 2012 @ 20:08:58 #142

Riparius

quote:
Op maandag 14 mei 2012 18:25 schreef thabit het volgende:

[..]

Is in het algemeen niet te doen, alleen in speciale gevallen. Dit soort kwadratische recursies spelen zelfs een belangrijke rol in de chaostheorie. Je kunt er ook fractals mee maken, zoals de Mandelbrotverzameling.

Een voorbeeld van eentje die nog wel te doen is (ik verklap de oplossing nog niet):
a₁ = 1/3, a_n+1 = 2a_n² - 1.

Tja, da's een leuke. Als kutkloon nu z'n goniometrische identiteiten maar goed kent ...

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

maandag 14 mei 2012 @ 22:38:06 #143

UbiDubiumIbiLibertas

Iemand een idee of deze figuur een (wiskundige) naam heeft?

maandag 14 mei 2012 @ 22:42:26 #144

thabit

Dat heet een gelijkzijdige driehoek met middenparallellen.

vrijdag 18 mei 2012 @ 21:46:16 #145

Anoonumos

Ik zoek de extremen van
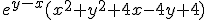
$e^{y-x}(x^2 + y^2+ 4x -4y +4)$
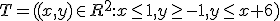
op het gebied $T = {((x,y) \in R^2: x \leq 1, y \geq -1, y \leq x + 6)$

Ik weet alleen niet wat ik kan zeggen over het punt (1,1), een hoekpunt van de driehoek T. Het is geen globaal max/min, maar is het een lokaal max/min?
Weet iemand hoe ik dit kan aanpakken?

vrijdag 18 mei 2012 @ 21:49:22 #146

thabit

Begin maar eens met de afgeleiden uit te rekenen.

vrijdag 18 mei 2012 @ 22:12:36 #147

Anoonumos

De gradient in (1,-1) heeft een negatieve x-component en een positieve y-component, oftewel in de richting van gebied T. Dus dan is f(1,-1) een lokaal minimum.
Bedankt.

zaterdag 19 mei 2012 @ 21:22:30 #148

Aardappel2610

Even een vraagje over het oplossen van goniometrische formules: Als ik de formule sin (2x) = sin(1/2 pi - 3x) probeer op te lossen krijg ik een -x in het geval van pi - x. Ik vraag mij eigenlijk af of het valide is om in zulke gevallen de - naar recht te verplaatsten, zodat er een gewone x ontstaat.

Forum Opties
Forumhop:
Hop naar:	(afkorting, bv 'KLB')

» school, studie en onderwijs

» school, studie en onderwijs