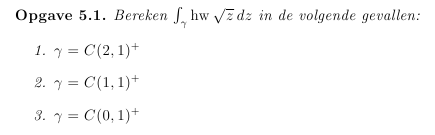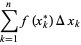SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Ik ben bezig met het doorwerken van Basisboek Wiskunde maar loop nu wat vast bij de vlakken. Er wordt gevraagd een vergelijking van een vlak op te stellen door drie gegeven punten, en die kan ik vinden, maar ik snap er een deel niet van.
Met als voorbeeld de drie punten A(2,0,0), B(0,3,0) en C(0,0,4) in een stelsel Oxyz vind ik als volgt de vergelijking van de twee lijnen door A & B en B & C
(2-0)(y-3) = (0-3)(x-0)
2(y-3) = -3x
2y - 6 = -3x
2y + 3x = 6
(3-0)(z-4) = (0-4)(y-0)
3(z-4) = -4y
3z - 12 = -4y
3z + 4y = 12
Volgens een vriend kon je ze dan vermenigvuldigen met d, gelijkstellen en bij elkaar voegen, en dat is waar ik het kwijt raak.
2dy + 3dx = 6d
3dz + 4dy = 12d
2dy + 3dx = 6d
(3/2)dz + 2dy = 6d
3dx + 2dy + (3/2)dz = 6d
Vanaf daar begrijp ik het wel weer, d = 1
3x + 2y + (3/2)z = 6
En er fancy uit laten zien
(3/6)x + (2/6)y + (3/12)z = 1
(x/2) + (y/3) + (z/4) = 1
Ik zie in dit alles het vlak als een bundeling lijnen vanuit punt B met als 'uiterste' lijnen de twee in het begin gevonden vergelijkingen, waarin iedere lijn gelimiteerd is door de d uit ax + by + cz = d. Is dit juist, of zit ik daarin fout?
Met als voorbeeld de drie punten A(2,0,0), B(0,3,0) en C(0,0,4) in een stelsel Oxyz vind ik als volgt de vergelijking van de twee lijnen door A & B en B & C
(2-0)(y-3) = (0-3)(x-0)
2(y-3) = -3x
2y - 6 = -3x
2y + 3x = 6
(3-0)(z-4) = (0-4)(y-0)
3(z-4) = -4y
3z - 12 = -4y
3z + 4y = 12
Volgens een vriend kon je ze dan vermenigvuldigen met d, gelijkstellen en bij elkaar voegen, en dat is waar ik het kwijt raak.
2dy + 3dx = 6d
3dz + 4dy = 12d
2dy + 3dx = 6d
(3/2)dz + 2dy = 6d
3dx + 2dy + (3/2)dz = 6d
Vanaf daar begrijp ik het wel weer, d = 1
3x + 2y + (3/2)z = 6
En er fancy uit laten zien
(3/6)x + (2/6)y + (3/12)z = 1
(x/2) + (y/3) + (z/4) = 1
Ik zie in dit alles het vlak als een bundeling lijnen vanuit punt B met als 'uiterste' lijnen de twee in het begin gevonden vergelijkingen, waarin iedere lijn gelimiteerd is door de d uit ax + by + cz = d. Is dit juist, of zit ik daarin fout?
"Social order at the expense of liberty is hardly a bargain."


Parametervergelijking:
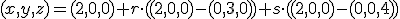
Hierbij uitgegaan van punt A met richtingsvectoren geconstrueerd uit A-B en A-C
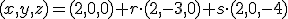
Bepaal de normaalvector door het kruisproduct nemen
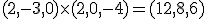
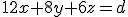
Vul een punt in om d te vinden:
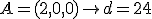
Invullen en uitschrijven:
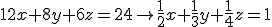
Hierbij uitgegaan van punt A met richtingsvectoren geconstrueerd uit A-B en A-C
Bepaal de normaalvector door het kruisproduct nemen
Vul een punt in om d te vinden:
Invullen en uitschrijven:


Daar ga ik zo mee aan de gang, bedankt.
"Social order at the expense of liberty is hardly a bargain."


De vergelijkingen die je geeft stellen in de driedimensionale ruimte vlakken voor, geen lijnen, dus hier gaat het al fout.quote:Op vrijdag 11 mei 2012 17:53 schreef Quir het volgende:
Ik ben bezig met het doorwerken van Basisboek Wiskunde maar loop nu wat vast bij de vlakken. Er wordt gevraagd een vergelijking van een vlak op te stellen door drie gegeven punten, en die kan ik vinden, maar ik snap er een deel niet van.
Met als voorbeeld de drie punten A(2,0,0), B(0,3,0) en C(0,0,4) in een stelsel Oxyz vind ik als volgt de vergelijking van de twee lijnen door A & B en B & C
Het idee is dat je eerst een normaalvector n bepaalt van je vlak V. Dat is een vector die loodrecht op het vlak staat. Is nu v = (x,y,z) een willekeurige vector met eindpunt in je vlak V en v0 = (x0,y0,z0) een vaste vector met eindpunt in je vlak, dan is vector v - v0 evenwijdig aan je vlak en staat deze verschilvector dus loodrecht op je normaalvector n, zodat het inproduct van v- v0 en n gelijk is aan nul:
(1) n∙(v - v0) = 0
En dus geldt ook:
(2) n∙v = n∙v0
Een vaste vector v0 met eindpunt in je vlak V ken je al omdat je immers de drie punten A,B en C kent die in vlak V liggen, zodat je hier voor v0 bijvoorbeeld de vector a = (2,0,0) zou kunnen nemen zodat x0 =2, y0 = 0 en z0 = 0.
De kunst is nu om een geschikte normaalvector n = (a,b,c) te bepalen want dan kun je voor (1) schrijven:
(3) a(x - x0) + b(y - y0) + c(z - z0) = 0,
en voor (2) kun je schrijven:
(4) ax + by + cz = ax0 + by0 + cz0,
en (3) of (4) is uiteraard de gezochte cartesische vergelijking van je vlak. Om nu een geschikte normaalvector n = (a,b,c) en daarmee de waarden van a,b en c te vinden kun je bedenken dat n loodrecht staat op zowel de verschilvector b - a als de verschilvector c - a, aangezien deze beide verschilvectoren evenwijdig zijn aan vlak V. En dus moet het inproduct van n = (a,b,c) met zowel b - a = (-2,3,0) als c - a = (-2,0,4) gelijk zijn aan nul. Dit geeft:
(5a) -2a + 3b = 0
(5b) -2a + 4c = 0
Hier heb je twee lineaire vergelijkingen in drie onbekenden a, b en c, en dus lijkt het alsof je nog één lineaire vergelijking tekort komt. Maar dat is niet zo, want als we n met een scalar vermenigvuldigen, dan hebben we nog steeds een vector die loodrecht op vlak V staat, dus zijn a,b,c niet eenduidig bepaald. Dat is ook meteen duidelijk uit de cartesische vergelijking (3) want als je hier beide leden met een getal ongelijk nul vermenigvuldigt, dan heb je nog steeds een geldige cartesische vergelijking van je vlak V.
We kunnen nu met (5a) en (5b) de waarde van a en b uitdrukken in c. Uit (5b) volgt dat a = 2c en substitutie hiervan in (5a) levert b = (4/3)∙c en dus hebben we n = (2c, (4/3)∙c, c). Kiezen we nu bijvoorbeeld c = 3, dan krijgen we n = (6, 4, 3). Op grond van (3) wordt de cartesische vergelijking van je vlak V nu:
(6) 6(x - 2) + 4(y - 0) + 3(z - 0) = 0,
en uitwerken hiervan geeft:
(7) 6x + 4y + 3z = 12
Je kunt nu door invullen gemakkelijk controleren dat de coördinaten van de punten A, B en C inderdaad aan (7) voldoen. Overigens hadden we in dit speciale geval de vergelijking van het vlak direct uit het hoofd kunnen opschrijven in de vorm (1/2)∙x + (1/3)∙y + (1/4)∙z = 1 omdat van elk van de drie gegeven punten A resp. B resp. C alleen de x- resp. y- resp. z-coördinaat ongelijk is aan nul. Maar in het algemeen is dat uiteraard niet zo als je de cartesische vergelijking van een vlak door drie gegeven punten op moet stellen.
[ Bericht 1% gewijzigd door Riparius op 12-05-2012 02:21:53 ]


Het is niet het superscript van de formulequote:Op donderdag 10 mei 2012 18:39 schreef Riparius het volgende:
[..]
Als je met die 10 het grondtal bedoelt van de logaritme, dan moet je dat wel superscripten, anders sticht je alleen maar verwarring. Dus:
L = 10log(I/I0)
Verder kun je gewoon gebruik maken van de definitie van de logaritme: glog a is de exponent waartoe je g moet verheffen om a te verkrijgen. Hier is L dus de macht waartoe je 10 moet verheffen om I/I0 te verkrijgen:
10L = I/I0


Ik begrijp niet wat je bedoelt, en in ieder geval sticht je verwarring, precies zoals ik al zei. Als je 10 een factor is dan moet je 10∙log(I/I0) schrijven en ook het grondtal van je logaritme specificeren, want het symbool log is ambigu.quote:Op vrijdag 11 mei 2012 22:11 schreef TheDutchguy het volgende:
[..]
Het is niet het superscript van de formule


Ik schreef de formule precies over uit mijn BINAS. Ik ga er in ieder geval van uit dat het 10 * is, maar is ook niet duidelijk aangegeven. Er staat L = 10 log(I/I0)quote:Op vrijdag 11 mei 2012 22:19 schreef Riparius het volgende:
[..]
Ik begrijp niet wat je bedoelt, en in ieder geval sticht je verwarring, precies zoals ik al zei. Als je 10 een factor is dan moet je 10∙log(I/I0) schrijven en ook het grondtal van je logaritme specificeren, want het symbool log is ambigu.


Je moet inderdaad met 10 vermenigvuldigen (en 10 is ook het grondtal geloof ik) om het geluidsniveau in dB (deciBell) te krijgen. Als je die 10 weglaat krijg je het in B (Bell).


Goed. Aangenomen dat Briggse logaritmen (grondtal 10) bedoeld zijn krijgen we dan:quote:Op vrijdag 11 mei 2012 22:50 schreef TheDutchguy het volgende:
[..]
Ik schreef de formule precies over uit mijn BINAS. Ik ga er in ieder geval van uit dat het 10 * is, maar is ook niet duidelijk aangegeven. Er staat L = 10 log(I/I0)
I = I0∙10L/10
Wat is hier nu moeilijk aan?


Ik heb nog wat moeite met hoe complexe integralen werken.
De eerste is niet zo moeilijk. De functie is holomorf op een omgeving van de afsluiting van D = C(2,1), gesloten kromme, dus 0.
Bij de tweede gaat het al fout, omdat hw sqrt{z} niet gedefinieerd is in 't punt 0. Maar ik kan geloof ik niet de residuenstelling gebruiken, want dan moet het een geisoleerde singulariteit zijn, maar op die hele lijn (-\infty, 0] bestaat de functie niet.
De eerste is niet zo moeilijk. De functie is holomorf op een omgeving van de afsluiting van D = C(2,1), gesloten kromme, dus 0.
Bij de tweede gaat het al fout, omdat hw sqrt{z} niet gedefinieerd is in 't punt 0. Maar ik kan geloof ik niet de residuenstelling gebruiken, want dan moet het een geisoleerde singulariteit zijn, maar op die hele lijn (-\infty, 0] bestaat de functie niet.


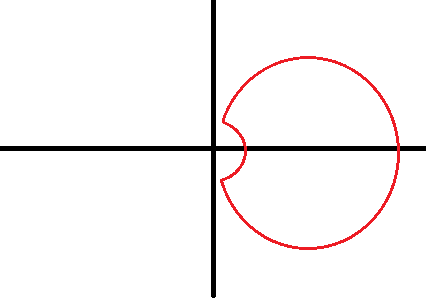
Bij de tweede kun je over een deel van de cirkel integreren dat 0 niet bevat, en dan een limiet daarvan nemen zodat je pad in de limiet de hele cirkel is.quote:Op zaterdag 12 mei 2012 16:08 schreef Hanneke12345 het volgende:
Ik heb nog wat moeite met hoe complexe integralen werken.
[ afbeelding ]
De eerste is niet zo moeilijk. De functie is holomorf op een omgeving van de afsluiting van D = C(2,1), gesloten kromme, dus 0.
Bij de tweede gaat het al fout, omdat hw sqrt{z} niet gedefinieerd is in 't punt 0. Maar ik kan geloof ik niet de residuenstelling gebruiken, want dan moet het een geisoleerde singulariteit zijn, maar op die hele lijn (-\infty, 0] bestaat de functie niet.


Zoiets dus?
Kun je dan gewoon zeggen dat die limiet gelijk is aan de integraal? En de integraal over elk van die met dat halve bolletje eruit is 0 (zelfde argument als bij (a)) dus is het 0? Maar bij de derde werkt ook die truc niet meer, en is er nog altijd geen geisoleerde singulariteit
Kun je dan gewoon zeggen dat die limiet gelijk is aan de integraal? En de integraal over elk van die met dat halve bolletje eruit is 0 (zelfde argument als bij (a)) dus is het 0? Maar bij de derde werkt ook die truc niet meer, en is er nog altijd geen geisoleerde singulariteit


De hoofdwaarde van √z voor z = r∙eiφ met -π < φ ≤ π en r ≥ 0 is √r∙eiφ/2 en daarmee gedefinieerd voor elke z ∈C. Maar inderdaad is deze functie alleen holomorf op C\(-∞,0].quote:Op zaterdag 12 mei 2012 16:08 schreef Hanneke12345 het volgende:
Ik heb nog wat moeite met hoe complexe integralen werken.
[ afbeelding ]
De eerste is niet zo moeilijk. De functie is holomorf op een omgeving van de afsluiting van D = C(2,1), gesloten kromme, dus 0.
Bij de tweede gaat het al fout, omdat hw sqrt{z} niet gedefinieerd is in 't punt 0. Maar ik kan geloof ik niet de residuenstelling gebruiken, want dan moet het een geisoleerde singulariteit zijn, maar op die hele lijn (-\infty, 0] bestaat de functie niet.


Bij ons is het geloof ik -π < φ < π, maar dat weet ik niet zeker. Kan ik zo gauw ook niet terugvidnen.


Je moet dan wel de integraal over dat kleine cirkeltje dan afschatten en laten zien dat dat in de limiet naar 0 gaat.quote:Op zaterdag 12 mei 2012 19:59 schreef Hanneke12345 het volgende:
Zoiets dus?
[ afbeelding ]
Kun je dan gewoon zeggen dat die limiet gelijk is aan de integraal? En de integraal over elk van die met dat halve bolletje eruit is 0 (zelfde argument als bij (a)) dus is het 0? Maar bij de derde werkt ook die truc niet meer, en is er nog altijd geen geisoleerde singulariteit
Bij de derde kun je het gewoon direct parametriseren.


Inderdaad, bij het tweede geval kom je door een limietbeschouwing tot de conclusie dat de integraal langs γ ook hier nul moet zijn, want de integraal langs de gesloten curve in je plaatje blijft 0, hoe klein je het boogje rond de oorsprong ook maakt.quote:Op zaterdag 12 mei 2012 19:59 schreef Hanneke12345 het volgende:
Zoiets dus?
[ afbeelding ]
Kun je dan gewoon zeggen dat die limiet gelijk is aan de integraal? En de integraal over elk van die met dat halve bolletje eruit is 0 (zelfde argument als bij (a)) dus is het 0? Maar bij de derde werkt ook die truc niet meer, en is er nog altijd geen geisoleerde singulariteit
Voor de derde opgave heb je z(φ) = eiφ als parametervoorstelling van je curve.


Kun je met dat bolletje niet zeggen dat de functie holomorf is op een omgeving van de afsluiting van dat gebied, en dus (stelling) dat de integraal over de rand 0 is? Omdat het dan weer gewoon een gesloten kromme is enzo.
Die derde ga ik even proberen met parametrizeren.
Die derde ga ik even proberen met parametrizeren.


De integraal over zo'n gesloten kromme is inderdaad 0, maar je moet nog wel aantonen dat alles in de limiet ook goed gaat. In dit voorbeeld is dat vrijwel triviaal, maar 't is wel goed om je daar in het algemeen bewust van te zijn.quote:Op zaterdag 12 mei 2012 20:18 schreef Hanneke12345 het volgende:
Kun je met dat bolletje niet zeggen dat de functie holomorf is op een omgeving van de afsluiting van dat gebied, en dus (stelling) dat de integraal over de rand 0 is? Omdat het dan weer gewoon een gesloten kromme is enzo.
Die derde ga ik even proberen met parametrizeren.


RIemann som
Ik heb 6 VWO WisB al afgerond, en iemand in het examentopic kwam aanzetten dat we Riemann sommen moeten beheersen (ofwel invoeren op de GR)
Maar hoe moest dat ookalweer!?
Ik gebruik Mathprint instellingen op de GR, als ik dan die somrij pak, welke waarden moet ik dan invullen? Ik ben heel die rotzooi vergeten
Gaan we even uit van de vraag dat ik de oppervlakte van x=2 tot x=24 wil weten van de functie 3^x - 9x
En ja, ik zou hier ook gewoon een integraal voor kunnen pakken, maar het gaat me nu specifiek om de Riemannsom
[ Bericht 16% gewijzigd door #ANONIEM op 13-05-2012 11:45:31 ]
Ik heb 6 VWO WisB al afgerond, en iemand in het examentopic kwam aanzetten dat we Riemann sommen moeten beheersen (ofwel invoeren op de GR)
Maar hoe moest dat ookalweer!?
Ik gebruik Mathprint instellingen op de GR, als ik dan die somrij pak, welke waarden moet ik dan invullen? Ik ben heel die rotzooi vergeten
Gaan we even uit van de vraag dat ik de oppervlakte van x=2 tot x=24 wil weten van de functie 3^x - 9x
En ja, ik zou hier ook gewoon een integraal voor kunnen pakken, maar het gaat me nu specifiek om de Riemannsom
[ Bericht 16% gewijzigd door #ANONIEM op 13-05-2012 11:45:31 ]


Je moet die xk op je intervalletje invullen waarvoor f(x) het grootst is, en ook de xk waarvoor f(x) het kleinst is.


Op Thabits manier krijg je een bovensom en ondersom (dus een bovengrens en ondergrens voor de integraal). Je kan ook steeds op ieder interval [xk, xk+1] de waarden in het midden nemen en daar f evalueren. Dan krijg je iets wat direct wat dichter bij de integraal zal zitten dan de ondersom of bovensom, en het is ook wat makkelijker te berekenen omdat je niet het supremum of infimum op ieder intervalletje hoeft te bepalen (dan moet je steeds nagaan of de functie daalt of stijgt op dat interval, etc).
Voorbeeld: Je moet het interval [2,24] opdelen in kleine deelintervalletjes. Je kan als grootte van die deelintervalletjes bijvoorbeeld 1 nemen (hoe kleiner, hoe dichter je bij de werkelijke integraal komt). Als je f dan steeds op de middens van die deelintervalletjes evalueert, moet je dus het volgende berekenen:
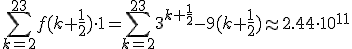
Terwijl
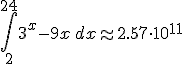
Dus dat zit nog redelijk in de buurt, ondanks het feit dat ik zulke grote deelintervallen heb genomen en je functie zo ontzettend hard stijgt .
.
Voorbeeld: Je moet het interval [2,24] opdelen in kleine deelintervalletjes. Je kan als grootte van die deelintervalletjes bijvoorbeeld 1 nemen (hoe kleiner, hoe dichter je bij de werkelijke integraal komt). Als je f dan steeds op de middens van die deelintervalletjes evalueert, moet je dus het volgende berekenen:
Terwijl
Dus dat zit nog redelijk in de buurt, ondanks het feit dat ik zulke grote deelintervallen heb genomen en je functie zo ontzettend hard stijgt


Wat wil je oplossen? Wat is six?quote:Op zondag 13 mei 2012 13:24 schreef PizzaGeit het volgende:
Hoe los ik dit op?
Ik streepte deen de
tegen elkaar weg:
Klopt dit?
(six=6 ziet er wel logisch uit, net zoiets als two = 2?