EXA Examenforum
En ze zijn er weer! Examens. Deel je leed, je irritaties, je blijdschap en nog veel meer met je mede FOK!kers.



Woensdag 16 mei, van 13:30 tot 16:30 buigen vast velen met mij zich over opgaven goniometrie, integraal- en differentiaalrekening, logaritmen en bewijzen in de meetkunde.
Vergeet vooral je:
Passer
Pen
Potloden
Gum
Geodriehoek
GR met programma's
Goede zin
niet
CE 1e tijdvak is geweest:
Voor de liefhebbers:
OPGAVEN
http://www.havovwo.nl/vwo/vwb/bestanden/vwb12iopg.pdf
UITWERKBIJLAGE
http://www.havovwo.nl/vwo/vwb/bestanden/vwb12ibl.pdf
OMZETTINGSTABEL:
http://www.havovwo.nl/vwo/vwb/bestanden/vwb12itab.pdf
CORRECTIEMODEL:
http://www.havovwo.nl/vwo/vwb/bestanden/vwb12iant.pdf
[ Bericht 40% gewijzigd door motorbloempje op 17-05-2012 14:18:28 ]
Vergeet vooral je:
Passer
Pen
Potloden
Gum
Geodriehoek
GR met programma's
Goede zin
niet
CE 1e tijdvak is geweest:
Voor de liefhebbers:
OPGAVEN
http://www.havovwo.nl/vwo/vwb/bestanden/vwb12iopg.pdf
UITWERKBIJLAGE
http://www.havovwo.nl/vwo/vwb/bestanden/vwb12ibl.pdf
OMZETTINGSTABEL:
http://www.havovwo.nl/vwo/vwb/bestanden/vwb12itab.pdf
CORRECTIEMODEL:
http://www.havovwo.nl/vwo/vwb/bestanden/vwb12iant.pdf
[ Bericht 40% gewijzigd door motorbloempje op 17-05-2012 14:18:28 ]


Staatsexamen, dus ik heb niks aan mijn gemiddelde van een 9,0 
Ik doe trouwens mijn mondeling over de Voortgezette Integraalrekening! Vandaag het laatste proefwerk maken, en dan verder met Wiskunde D ofzo.
Ik doe trouwens mijn mondeling over de Voortgezette Integraalrekening! Vandaag het laatste proefwerk maken, en dan verder met Wiskunde D ofzo.


MOOI! ik moet profiel kiezen dit jaar en ik ga het gewoon op wiskunde A houden, denk ik :p
"Ik vind Marcellis wel zo iemand die er op zijn 28e achter komt dat hij eigenlijk linksbenig is." - Tim86
"Marcellis legt ze zo op de stropdas. Mits ze een stropdas van 8 meter aan zouden hebben." - Toefjes
kortom:
"Marcellis legt ze zo op de stropdas. Mits ze een stropdas van 8 meter aan zouden hebben." - Toefjes
kortom:


quote:Op dinsdag 27 maart 2012 07:22 schreef TBakkert het volgende:
MOOI! ik moet profiel kiezen dit jaar en ik ga het gewoon op wiskunde A houden, denk ik :p


Hoeft niet, dat ligt totaal aan de persoon.quote:
De ene persoon kan beter abstract denken dan de andere en heeft daardoor weinig moeite met wiskunde B. Wiskunde A vereist weer andere inzichten.
You can see my personality being reflected in this post: 1 part Intelligence and 3 parts Awesomeness.


tof! en toch vind ik het nog altijd belachelijk dat je er een programmeerbare rekenmachine bij mag houden. hou er rekening mee dat je dat bij een vervolgopleiding die iets waard is, niet mag 
Your mind don't know how you're taking all the shit you see
Dont believe anyone but most of all dont believe me
God damn right it's a beautiful day Uh-huh
Dont believe anyone but most of all dont believe me
God damn right it's a beautiful day Uh-huh


Dat snap ik inderdaad ook niet...quote:Op dinsdag 27 maart 2012 09:14 schreef simmu het volgende:
tof! en toch vind ik het nog altijd belachelijk dat je er een programmeerbare rekenmachine bij mag houden. hou er rekening mee dat je dat bij een vervolgopleiding die iets waard is, niet mag


Mijn algebra is prima. Voor het plotten van functies is hij heel handig. Controle.quote:Op dinsdag 27 maart 2012 09:14 schreef simmu het volgende:
tof! en toch vind ik het nog altijd belachelijk dat je er een programmeerbare rekenmachine bij mag houden. hou er rekening mee dat je dat bij een vervolgopleiding die iets waard is, niet mag
Uiteindelijk dien je de shit toch algebraïsch uit te werken!
ANW proefwerk zit er nu op, zodirect Engels, dan Scheikunde en dan Wiskunde. 4 proefwerken vandaag.


Hier kijk ik het minst tegenop.
Ik heb al twee jaar echt een fantastische docente en de structuur van de lessen is heel fijn, vanaf het begin af aan ook veel herhaling.
We oefenen vaak ook op iets hoger niveau zodat het uiteindelijk 'meevalt'. Moet wel goedkomen
Ik heb al twee jaar echt een fantastische docente en de structuur van de lessen is heel fijn, vanaf het begin af aan ook veel herhaling.
We oefenen vaak ook op iets hoger niveau zodat het uiteindelijk 'meevalt'. Moet wel goedkomen


Rekenmachine lobby bij de overheid. Lekker de prijzen opschroeven, omdat iedere scholier er één moet.quote:
Noodles


Mensen die iets willen verbieden waardoor je alle theorie in je rekenmachine kan zetten.quote:Op dinsdag 27 maart 2012 09:14 schreef simmu het volgende:
tof! en toch vind ik het nog altijd belachelijk dat je er een programmeerbare rekenmachine bij mag houden. hou er rekening mee dat je dat bij een vervolgopleiding die iets waard is, niet mag
It was an opportunity to honour our memories and to make room for new ones


Wiskunde B  Het enige lichtpuntje van mijn middelbare school carriere wat ik vorig jaar heb afgesloten
Het enige lichtpuntje van mijn middelbare school carriere wat ik vorig jaar heb afgesloten 
Do you think you will walk away untested?


Wiskunde 
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Leukste vak, helaas nooit echt iets voor gedaan en dus nooit goed gesnapt (met een 5 of 6 overgaan enzo)  Nu ik alles goed begin te snappen is het een stuk leuker en samenhangender, en vind ik het zonde dat ik hier altijd laag voor gehaald heb..
Nu ik alles goed begin te snappen is het een stuk leuker en samenhangender, en vind ik het zonde dat ik hier altijd laag voor gehaald heb..


Tot mijn grote verbazing vielen de cijfers voor juist dit vak mee dit jaar. Hopen op een 8 gemiddeld uiteindelijk.
Not everything that counts can be counted, and not everything that can be counted counts


Ik heb hetzelfde, afgelopen jaren geen flikker er voor gedaan, altijd slechte cijfers halen. Maar nu begin ik het echt goed door te krijgen en begin ik er ook lol in te krijgen.quote:Op donderdag 5 april 2012 16:35 schreef dramatic het volgende:
Leukste vak, helaas nooit echt iets voor gedaan en dus nooit goed gesnapt (met een 5 of 6 overgaan enzo)Nu ik alles goed begin te snappen is het een stuk leuker en samenhangender, en vind ik het zonde dat ik hier altijd laag voor gehaald heb..
.


één vraag van 8 punten, en 2 van 6 punten. Bewijzen/tekenen?
Ik kijk trouwens ook wel naar het examen uit
Ik sta nu een 8.2, en wil in ieder geval een 9 afgerond komen te staan. Hoop dat ik ongeveer hetzelfde kan halen als met de oefentoetsen, dan komt dat zeker goed.
Ik kijk trouwens ook wel naar het examen uit
Ik sta nu een 8.2, en wil in ieder geval een 9 afgerond komen te staan. Hoop dat ik ongeveer hetzelfde kan halen als met de oefentoetsen, dan komt dat zeker goed.
26"
Fading slowly.
Fading slowly.


Acht punten voor tekenen/bewijzen? Oh alsjeblieft niet zeg 
Liever voor een uitgebreide vraag met e en ln ofzo
Knap van je gemiddelde wel Unsub, negen gemiddeld moet idd wel te halen zijn als je goed examens oefent!
Liever voor een uitgebreide vraag met e en ln ofzo
Knap van je gemiddelde wel Unsub, negen gemiddeld moet idd wel te halen zijn als je goed examens oefent!


quote:Op maandag 30 april 2012 11:11 schreef Lutte het volgende:
Acht punten voor tekenen/bewijzen? Oh alsjeblieft niet zeg
Liever voor een uitgebreide vraag met e en ln ofzo
Knap van je gemiddelde wel Unsub, negen gemiddeld moet idd wel te halen zijn als je goed examens oefent!
26"
Fading slowly.
Fading slowly.


Vandaag 4 uir proefexamen gehad. Nog hard oefenen op bewijzen... Ik zit nu een oefenexamen ( VWO 2010 TV2), en dan lukt het wel vlot. kenserdedjenser


Gvd zin in 
Een dikke 9 gemiddeld voor WisB. Ik wil proberen een 10 te scoren! Genoeg >9,5 cijfers gescoord dit jaar. 9,6 voortgezette integraalrekening, 9,5 voor gonio... maar... een 4,8 voor Bewijs in de vlakke meetkunde. Alhoewel dat wel een heel zwaar proefwerk was. Had m'n wiskundedocent zelf gemaakt.. Die op de proefexamens waren veel simpeler!
Sterkste punt is hier toch wel echt de integraalrekening!
Een dikke 9 gemiddeld voor WisB. Ik wil proberen een 10 te scoren! Genoeg >9,5 cijfers gescoord dit jaar. 9,6 voortgezette integraalrekening, 9,5 voor gonio... maar... een 4,8 voor Bewijs in de vlakke meetkunde. Alhoewel dat wel een heel zwaar proefwerk was. Had m'n wiskundedocent zelf gemaakt.. Die op de proefexamens waren veel simpeler!
Sterkste punt is hier toch wel echt de integraalrekening!


Bewijzen zijn dan ook niet te doen. Die hebben er bij ons elk tentamen ingezeten voor 1/6 van de punten of meer, waardoor het dus onmogelijk was 9.5 te scoren. De grap is dat die vragen ook echt 10 punten waren itt die 4punten vragen op het examen. Ofwel, veel meer stappen nodig wat ze nog moeilijker maken.quote:Op zaterdag 12 mei 2012 06:26 schreef Amoeba het volgende:
Gvd zin in
Een dikke 9 gemiddeld voor WisB. Ik wil proberen een 10 te scoren! Genoeg >9,5 cijfers gescoord dit jaar. 9,6 voortgezette integraalrekening, 9,5 voor gonio... maar... een 4,8 voor Bewijs in de vlakke meetkunde. Alhoewel dat wel een heel zwaar proefwerk was. Had m'n wiskundedocent zelf gemaakt.. Die op de proefexamens waren veel simpeler!
Sterkste punt is hier toch wel echt de integraalrekening!


Jup, en die van de 10 jaar ervoor zijn er ook te vinden.. Dus?quote:Op zaterdag 12 mei 2012 09:21 schreef Borizzz het volgende:
Het wiskunde B examen van vorig jaar. Beide tijdvakken & de uitwerkingen.
26"
Fading slowly.
Fading slowly.


Al gemaakt.quote:Op zaterdag 12 mei 2012 09:21 schreef Borizzz het volgende:
Het wiskunde B examen van vorig jaar. Beide tijdvakken & de uitwerkingen.
[ Bericht 0% gewijzigd door #ANONIEM op 12-05-2012 12:03:07 ]


Nee als in: Specificatiequote:Op zaterdag 12 mei 2012 16:00 schreef Unsub het volgende:
[..]
Als in: "jullie kunnen integreren?" bedoel je?
De kandidaat kan:
11.1 bij daarvoor geëigende toepassingen een bepaalde integraal opstellen.
11.2 met behulp van de grafische rekenmachine een Riemannsom berekenen als benadering van een integraal


Riemannsom zelf niet, maar de kans dat ze dat vragen is zo klein. Gewoon integreren et cetera wel natuurlijkquote:Op zaterdag 12 mei 2012 16:02 schreef fixatoman het volgende:
[..]
Nee als in: Specificatie
De kandidaat kan:
11.1 bij daarvoor geëigende toepassingen een bepaalde integraal opstellen.
11.2 met behulp van de grafische rekenmachine een Riemannsom berekenen als benadering van een integraal


Je kan de riemannsom als reeks invoeren maar ik weet niet uit mn hoofd hoe.. Zal er maandag eens naar kijken, ik leer de examens gewoon op volgorde.quote:Op zaterdag 12 mei 2012 16:06 schreef Lutte het volgende:
[..]
Riemannsom zelf niet, maar de kans dat ze dat vragen is zo klein. Gewoon integreren et cetera wel natuurlijk


Die klote Riemannsommen kwamen even voor het integreren. Hoofdstuk 10 van Getal en Ruimte meende ik. Inderdaad even opzoeken hoe dat moet! Thanks


Komop jongens, help me even verder.
Ik gebruik mathprint instellingen, stel dat ik de grootte van de Riemannsom van het interval tussen x=2 en x=23 wil weten, hoe ziet mijn somfunctie er dan uit?
Van de functie 3^x - 9x - 6lnx
[ Bericht 9% gewijzigd door #ANONIEM op 13-05-2012 11:27:02 ]
Ik gebruik mathprint instellingen, stel dat ik de grootte van de Riemannsom van het interval tussen x=2 en x=23 wil weten, hoe ziet mijn somfunctie er dan uit?
Van de functie 3^x - 9x - 6lnx
[ Bericht 9% gewijzigd door #ANONIEM op 13-05-2012 11:27:02 ]


Je kan de mathprint ook uitzetten in mode als het niet lukt, ikzelf vind het somteken ook vaag ermee, maar ik zal het even proberenquote:Op zondag 13 mei 2012 11:22 schreef Amoeba het volgende:
Komop jongens, help me even verder.
Ik gebruik mathprint instellingen, stel dat ik de grootte van de Riemannsom van het interval tussen x=2 en x=23 wil weten, hoe ziet mijn somfunctie er dan uit?
Van de functie 3^x - 9x - 6lnx


Ik was er ook mee aan het klooien. Als ik dan als referentiemateriaal de integraal nam kwam ik vrij goed uit met x=.5 onderaan..?


Ik kwam net ook vrij goed uit, maar hoe doe je nu een linker of rechter grens.. ik neem nu aan dat onderin de stapgrootte staat, maar in dat geval kan je dus bovenin alleen zeggen tot waar, en niet vanaf welke waarde je de som neemt?quote:Op zondag 13 mei 2012 11:56 schreef Amoeba het volgende:
Ik was er ook mee aan het klooien. Als ik dan als referentiemateriaal de integraal nam kwam ik vrij goed uit met x=.5 onderaan..?
edit: zo werkt het dus niet


http://www.math.cmu.edu/~(...)2_f08_rhandout3a.pdf
pagina 5 nu nog lezen
nu nog lezen
dit ziet er echt uit als veel werk
pagina 5
dit ziet er echt uit als veel werk


Mwah, het is wel te doen.
Aantal rechthoeken -1 bovenaan.
onderaan x=0
formule invoeren
a = Xondergrens
neem voor x a+stapgrootte*x
heel de functie vermenigvuldigen met de stapgrootte
Aantal rechthoeken -1 bovenaan.
onderaan x=0
formule invoeren
a = Xondergrens
neem voor x a+stapgrootte*x
heel de functie vermenigvuldigen met de stapgrootte


ik heb bijna een screen, het lukte netquote:Op zondag 13 mei 2012 12:20 schreef Amoeba het volgende:
Mwah, het is wel te doen.
Aantal rechthoeken -1 bovenaan.
onderaan x=0
formule invoeren
a = Xondergrens
neem voor x a+stapgrootte*x
heel de functie vermenigvuldigen met de stapgrootte


Dit is dus linkergrens met N is 40
rechtergrens moet je dus gewoon N nemen ipv N-1 en onderin met X=1 beginnen
midden moet je dus gewoon N-.5 nemen en onderin met X=0.5 beginnen


Ik was bezig met een andere functie, maar dat kwam niet uit.
Ik heb maandag nog 2 uur Wiskunde, eens even tegen John zeggen dat hij Riemannsommen uit moet leggen voor de GR.
Ik heb maandag nog 2 uur Wiskunde, eens even tegen John zeggen dat hij Riemannsommen uit moet leggen voor de GR.


Nou goed, functie:
3^x - 9x
interval
-2 -> 2
stapgrootte: 0,05
dus n = 80-1 = 79
a = -2
het verschil met de integraal is 0,7...?
3^x - 9x
interval
-2 -> 2
stapgrootte: 0,05
dus n = 80-1 = 79
a = -2
het verschil met de integraal is 0,7...?


eens proberen, maar ik heb het idee dat ik gewoon die sum(seq( ga gebruikenquote:Op zondag 13 mei 2012 12:32 schreef Amoeba het volgende:
Nou goed, functie:
3^x - 9x
interval
-2 -> 2
stapgrootte: 0,05
dus n = 80-1 = 79
a = -2
het verschil met de integraal is 0,7...?


Het blijft een een slechte benadering zo een reeks
toch een screenshot:
dat lijkt me bijna geen verschil
toch een screenshot:
dat lijkt me bijna geen verschil


Dat is dus het idee van ondergrens/bovengrens/middengrens. 3 verschillende manieren van de riemannsum waarbij de laatste het meest precies is. of hoe heet datquote:


Ik zoek het morgen sowieso wel uit op skool. Ik had trouwens het hele jaar shit in m'n GR gezet en nu gisteren sloot ik hem aan op de computer: RAM RESET toen hij vastliep
ja kut
Nu dat notefolio maar gebruikt voor m'n goniometrische formules
ja kut
Nu dat notefolio maar gebruikt voor m'n goniometrische formules


okee naja,
en bij midden pak je dus 0,5 en -0,5. En midden is dus preciezer dan die andere 2
toch vandaag geleerd die functie te gebruiken Ben nu dus officieel begonnen met wiskunde leren
Ben nu dus officieel begonnen met wiskunde leren 
en bij midden pak je dus 0,5 en -0,5. En midden is dus preciezer dan die andere 2
toch vandaag geleerd die functie te gebruiken


Bij die Lissajous-grafieken, nadat je die formules in de rekenmachine ingevoerd hebt (nadat je bij mode 'func' veranderd hebt in 'par'), wat moet je bij je venster-instellingen (window) voor Tstep invoeren?


1/48pi of zoiets. Echt kleine rotzooiquote:Op zondag 13 mei 2012 13:12 schreef PG18 het volgende:
Bij die Lissajous-grafieken, nadat je die formules in de rekenmachine ingevoerd hebt (nadat je bij mode 'func' veranderd hebt in 'par'), wat moet je bij je venster-instellingen (window) voor Tstep invoeren?


Wiskunde is peanuts. Hoop dat die Riemannsommen niet terugkomen, maar ik vraag het morgen nog gewoon eventjes na.quote:Op zondag 13 mei 2012 12:48 schreef dramatic het volgende:
okee naja,
[ afbeelding ]
en bij midden pak je dus 0,5 en -0,5. En midden is dus preciezer dan die andere 2
toch vandaag geleerd die functie te gebruikenBen nu dus officieel begonnen met wiskunde leren

a.s. dinsdag Informatica op het VWO, woensdag Wiskunde B!
Informatica nog eventjes leren.


School examen?quote:Op zondag 13 mei 2012 13:23 schreef Amoeba het volgende:
[..]
a.s. dinsdag Informatica op het VWO, woensdag Wiskunde B!
Informatica nog eventjes leren.


? Ik heb Informatica met een 8 afgesloten en heb geen CEquote:Op zondag 13 mei 2012 13:23 schreef Amoeba het volgende:
[..]
Wiskunde is peanuts. Hoop dat die Riemannsommen niet terugkomen, maar ik vraag het morgen nog gewoon eventjes na.
a.s. dinsdag Informatica op het VWO, woensdag Wiskunde B!
Informatica nog eventjes leren.


Ik doe geen regulier examen, maar staatsexamen.quote:Op zondag 13 mei 2012 13:43 schreef dramatic het volgende:
[..]
? Ik heb Informatica met een 8 afgesloten en heb geen CE
Van het Wiskundetopique. Mijn held.quote:Op zondag 13 mei 2012 13:19 schreef thenxero het volgende:
Op Thabits manier krijg je een bovensom en ondersom (dus een bovengrens en ondergrens voor de integraal). Je kan ook steeds op ieder interval [xk, xk+1] de waarden in het midden nemen en daar f evalueren. Dan krijg je iets wat direct wat dichter bij de integraal zal zitten dan de ondersom of bovensom, en het is ook wat makkelijker te berekenen omdat je niet het supremum of infimum op ieder intervalletje hoeft te bepalen (dan moet je steeds nagaan of de functie daalt of stijgt op dat interval, etc).
Voorbeeld: Je moet het interval [2,24] opdelen in kleine deelintervalletjes. Je kan als grootte van die deelintervalletjes bijvoorbeeld 1 nemen (hoe kleiner, hoe dichter je bij de werkelijke integraal komt). Als je f dan steeds op de middens van die deelintervalletjes evalueert, moet je dus het volgende berekenen:
Terwijl
Dus dat zit nog redelijk in de buurt, ondanks het feit dat ik zulke grote deelintervallen heb genomen en je functie zo ontzettend hard stijgt.


het blijft vaag met mathprintquote:Op zondag 13 mei 2012 13:50 schreef Amoeba het volgende:
[..]
Ik doe geen regulier examen, maar staatsexamen.
[..]
Van het Wiskundetopique. Mijn held.
[ Bericht 5% gewijzigd door dramatic op 13-05-2012 14:21:10 ]


Ok jongens ik help de mensen met een TI even uit de brand wat betreft de Riemannsom hij is erg eenvoudig:
sum(seq((y1)*breedte interval,x,linkergrens +half breedte interval, rechtergrens - half breedte interval, breedte interval)
Voer hem zo in op je rekenmachine
y1 staat uiteraard voor de functie die je wil primitiveren.
sum= 2nd stat (=list) MATH nr 5
seq=2nd stat(=list) OPS nr 5
sum(seq((y1)*breedte interval,x,linkergrens +half breedte interval, rechtergrens - half breedte interval, breedte interval)
Voer hem zo in op je rekenmachine
y1 staat uiteraard voor de functie die je wil primitiveren.
sum= 2nd stat (=list) MATH nr 5
seq=2nd stat(=list) OPS nr 5


Klopt zo kan het ook idd! Maar we proberen die nieuwe functie onder de knie te krijgenquote:Op zondag 13 mei 2012 15:42 schreef metanite het volgende:
Ok jongens ik help de mensen met een TI even uit de brand wat betreft de Riemannsom hij is erg eenvoudig:
sum(seq((y1)*breedte interval,x,linkergrens +half breedte interval, rechtergrens - half breedte interval, breedte interval)
Voer hem zo in op je rekenmachine
y1 staat uiteraard voor de functie die je wil primitiveren.
sum= 2nd stat (=list) MATH nr 5
seq=2nd stat(=list) OPS nr 5


Ok, maar jongens dit examen moet toch gewoon goed komen, enige vak naar mijn idee dat ze je niet voor idioot grote verassingen kunnen zetten. Ik schijt hem nu al voor Spaans, dat word gewoon multiplegok, zit je daar vrijdagmiddag als iedereen al zijn examens al heeft gehad nog in zo een lege zaal (kleine klas leerlingen > grote examenzaalquote:Op zondag 13 mei 2012 15:46 schreef dramatic het volgende:
[..]
Klopt zo kan het ook idd! Maar we proberen die nieuwe functie onder de knie te krijgen


Ik ben eruit maatje.
k=0, onderaan, altijd
Neem even het interval Ax=12 tot Bx=15
stapgrootte: 0,1
Y1(xk)*stapgrootte staat er tussen de haken, oke?
Xk = a+0,5*stapgrootte + stapgrootte*k
b bereken je als volgt:
Doe de eindwaarde - 0,5stapgrootte, in dit geval dus 15-0,05 = 14,95
Je laat k lopen van 0 tot een getal. Dit getal is als volgt
14,95 = Xk * k
Die waarde van k heb je nodig.
k=0, onderaan, altijd
Neem even het interval Ax=12 tot Bx=15
stapgrootte: 0,1
Y1(xk)*stapgrootte staat er tussen de haken, oke?
Xk = a+0,5*stapgrootte + stapgrootte*k
b bereken je als volgt:
Doe de eindwaarde - 0,5stapgrootte, in dit geval dus 15-0,05 = 14,95
Je laat k lopen van 0 tot een getal. Dit getal is als volgt
14,95 = Xk * k
Die waarde van k heb je nodig.


Ik wil een 10 scoren voor dit examen. ik heb me het hele jaar de pleuris ingezet voor Wiskunde, en wil dat godverdomme nu belonen. Met een staatsexamen nu, dus ik heb nog geen gemiddelde, als m'n cijfers tellen niet mee.quote:Op zondag 13 mei 2012 15:50 schreef metanite het volgende:
[..]
Ok, maar jongens dit examen moet toch gewoon goed komen, enige vak naar mijn idee dat ze je niet voor idioot grote verassingen kunnen zetten. Ik schijt hem nu al voor Spaans, dat word gewoon multiplegok, zit je daar vrijdagmiddag als iedereen al zijn examens al heeft gehad nog in zo een lege zaal (kleine klas leerlingen > grote examenzaal). In ieder geval succes met Nederlands morgen !
Laat dit lukken.


Dit dikgedrukte volg ik niet helaas. Kan je dat nog eens toelichten?quote:Op zondag 13 mei 2012 15:52 schreef Amoeba het volgende:
Ik ben eruit maatje.
k=0, onderaan, altijd
Neem even het interval Ax=12 tot Bx=15
stapgrootte: 0,1
Y1(xk)*stapgrootte staat er tussen de haken, oke?
Xk = a+0,5*stapgrootte + stapgrootte*k
b bereken je als volgt:
Doe de eindwaarde - 0,5stapgrootte, in dit geval dus 15-0,05 = 14,95
Je laat k lopen van 0 tot een getal. Dit getal is als volgt
14,95 = Xk * k
Die waarde van k heb je nodig.


Dat kan ik.quote:Op zondag 13 mei 2012 16:07 schreef dramatic het volgende:
[..]
Dit dikgedrukte volg ik niet helaas. Kan je dat nog eens toelichten?
Je hebt die vierkantjes getekend:
Met n vierkantjes.
Het laatste vierkantje ligt op x= Xb-.5stapgrootte
Dus wil je k laten lopen van 0 tot een waarde waarvoor f(Xk) gelijk is aan die laatste stapgrootte.
dus Xk * *diekwaarde


Riemanssom is de afgelopen 20 jaar niet op het examen gekomen  ik ging net examen 2011 tijdvak 2 maken, pfff die vond ik echt moeilijk joh!
ik ging net examen 2011 tijdvak 2 maken, pfff die vond ik echt moeilijk joh!


Daar zat toch juist die Riemannsum vraag in? iig een plaatje ervanquote:Op zondag 13 mei 2012 19:23 schreef zoodan het volgende:
Riemanssom is de afgelopen 20 jaar niet op het examen gekomenik ging net examen 2011 tijdvak 2 maken, pfff die vond ik echt moeilijk joh!


Nope, kans is ook heel klein dat je dat krijgt. We hebben er zelf ook heel weinig aandacht aan besteed tijdens de lessen. Het is meestal gewoon integreren.quote:Op zondag 13 mei 2012 19:36 schreef dramatic het volgende:
[..]
Daar zat toch juist die Riemannsum vraag in? iig een plaatje ervan


Ik kijk ook erg op tegen bewijzen, ik ken alle regels wel ect. maar ik mis dat inzicht om tot het antwoord te komen, iemand een tip?


Terug werken vanuit het antwoord:quote:Op maandag 14 mei 2012 11:05 schreef zoodan het volgende:
Ik kijk ook erg op tegen bewijzen, ik ken alle regels wel ect. maar ik mis dat inzicht om tot het antwoord te komen, iemand een tip?
Wat heb je nodig om die laatste stap te zetten om je bewijs te voltooien?
Wat heb je dan nodig om dat weer te bewijzen, en dit net zo lang herhalen totdat je op iets uitkomt dat gegeven is of dat al bewezen is.
Vervolgens kun je dan het bewijs in de juiste volgorde uitwerken.
You can see my personality being reflected in this post: 1 part Intelligence and 3 parts Awesomeness.


Terugwerken inderdaad, en heel goed kijken naar datgene dat is te bewijzen. Gebruik die uitdrukking, daarmee kun je vaak een sleutel tot de oplossing/goede redenatie vinden.
kloep kloep


Iemand die me deze stap kan uitleggen? (2011-1 vraag 9)
De bedoeling is om de afgeleide gelijk te stellen aan 0 en x daarmee uit te rekenen.
Dit heb ik met de GR gedaan, maar het moest algebraïsch .
.
Alleen ik snap niet hoe je die breuk om moet schrijven om tot die onderste te komen...
De bedoeling is om de afgeleide gelijk te stellen aan 0 en x daarmee uit te rekenen.
Dit heb ik met de GR gedaan, maar het moest algebraïsch
Alleen ik snap niet hoe je die breuk om moet schrijven om tot die onderste te komen...


Vermenigvuldig deze breuk eens met de breuk wortel (x) / wortel (x) (dus met 1) en vereenvoudig zover mogelijk.
kloep kloep


Held!quote:Op maandag 14 mei 2012 21:46 schreef Borizzz het volgende:
Vermenigvuldig deze breuk eens met de breuk wortel (x) / wortel (x) (dus met 1) en vereenvoudig zover mogelijk.


Morgen is de dag heren en dames. HAVO Economie & VWO Wiskunde B. Ik heb g v d zin in dit koningsexamen. 
Wiskunde B
Net VWO Informatica (College-examen) erop zitten, wel geslaagd denk ik, maar wat zaten daar k*tvragen in zeg.
Wiskunde B
Net VWO Informatica (College-examen) erop zitten, wel geslaagd denk ik, maar wat zaten daar k*tvragen in zeg.


Natuurlijk, de kans is klein,, maar het is maar een kleinigheidje, puur een kwestie van de formule intikken op je GRM, maar ik weet niet meer hoe. En het zou toch zonde zijn als je daar dan geen punten voor weet te behalen. Iemand trouwens nog een handige link/document over hoe je bewijzen het beste aan kan pakken? Dat is mijn enige zwakke punt.


http://www2.cito.nl/vo/ce(...)lder.htm?opening.htmquote:Op dinsdag 15 mei 2012 14:17 schreef PG18 het volgende:
Waar is dat pdf bestandje te vinden waarin staat hoeveel punten we per vraag krijgen?
Daar, en dan op het groene S'je klikken.


Nog een kleine tip, op IEDER examen komt volgensmij voor dat je de lengte van een lijn van een grafiek moet berekenen. Was iets met een integraal en een wortel uit mijn hoofd, weet niet meer exact wat de formule was. 


tjah ff in mn GR kijken, owja,quote:Op dinsdag 15 mei 2012 15:53 schreef Prulez het volgende:
Nog een kleine tip, op IEDER examen komt volgensmij voor dat je de lengte van een lijn van een grafiek moet berekenen. Was iets met een integraal en een wortel uit mijn hoofd, weet niet meer exact wat de formule was.
BOOGLENGTE
Grenzen x=a en x=b,
y1=functie'
y2=wortel(1+y1^2)
fnint(y2,x,a,b)


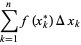



.png)
