SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



uh? ik wil gewoon graag een nummer ipv q. dat nummer is 0.02003
"Vanity, definitely my favorite sin. . . ."


steek maar meer moeite in het stellen van je vraag
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Je bedoeltquote:Op zaterdag 28 januari 2012 21:24 schreef One_conundrum het volgende:
uh? ik wil gewoon graag een nummer ipv q. dat nummer is 0.02003
Want dan is
Of bedoel je
Erg duidelijk ben je niet
Inderdaad.quote:Op zaterdag 28 januari 2012 21:30 schreef GlowMouse het volgende:
steek maar meer moeite in het stellen van je vraag


haha, Ik had niet verwacht dat mijn vraag zo onduidelijk was.quote:Op zaterdag 28 januari 2012 21:30 schreef GlowMouse het volgende:
steek maar meer moeite in het stellen van je vraag
Hmm er ontbreek natuurlijk iets. stom. Ik dacht dat dit stuk wel genoeg was...
nog es kijken dan
"Vanity, definitely my favorite sin. . . ."


100 - 1e -(0.04/12) = 100e -q/2
Zo dus. Nu is het logischer toch? hoe los ik nu q op?
Sorry van mijn eerdere fuck-up
Zo dus. Nu is het logischer toch? hoe los ik nu q op?
Sorry van mijn eerdere fuck-up
"Vanity, definitely my favorite sin. . . ."


Ik zal eens kijken 
[edit]
Zie voor het isoleren van q mijn post hierboven en zie 100-e-0.04/12 als a, dan:
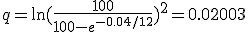
Ik heb geen GR bij de hand en geen zin om Matlab te starten, dus dat moet je zelf even intoetsen
[ Bericht 35% gewijzigd door zoem op 28-01-2012 22:22:08 ]
[edit]
Zie voor het isoleren van q mijn post hierboven en zie 100-e-0.04/12 als a, dan:
Ik heb geen GR bij de hand en geen zin om Matlab te starten, dus dat moet je zelf even intoetsen
[ Bericht 35% gewijzigd door zoem op 28-01-2012 22:22:08 ]


hmm het komt niet echt uit, ik krijg niet echt 0.02etc uit mijn GR..
het moet dus zijn uuuh
100 - 1e-(0.04/12) = 100e -(q/2)
99.003etc = 100e -(q/2)
het moet dus zijn uuuh
100 - 1e-(0.04/12) = 100e -(q/2)
99.003etc = 100e -(q/2)
"Vanity, definitely my favorite sin. . . ."


Je weet dat je ook lijntjes kan plotten op je GR?
y1 = 100e -(q/2)
y2 = 100 - 1e-(0.04/12)
Dan kun je het verloop van de vergelijking zien en met intersect heb je ook je antwoord
[edit]
Ah ik zie ik dat ik ben vergeten een 2 van de 1/2 te maken toen ik het naar "rechts" gooide.
Even fixen hierboven
[ Bericht 27% gewijzigd door zoem op 28-01-2012 22:21:27 ]
y1 = 100e -(q/2)
y2 = 100 - 1e-(0.04/12)
Dan kun je het verloop van de vergelijking zien en met intersect heb je ook je antwoord
[edit]
Ah ik zie ik dat ik ben vergeten een 2 van de 1/2 te maken toen ik het naar "rechts" gooide.
Even fixen hierboven
[ Bericht 27% gewijzigd door zoem op 28-01-2012 22:21:27 ]


99.003etc = 100e -(q/2)quote:Op zaterdag 28 januari 2012 22:07 schreef One_conundrum het volgende:
hmm het komt niet echt uit, ik krijg niet echt 0.02etc uit mijn GR..
het moet dus zijn uuuh
100 - 1e-(0.04/12) = 100e -(q/2)
99.003etc = 100e -(q/2)
99.003etc/100 = e -(q/2)
ln 99.003etc/100 = -(q/2)
-2*(ln 99.003etc/100) = q
De truc is dus om beide kanten maal ln te doen en dan valt de e weg.


Weer ff een vraag over statistiek:
5. Bij een tweezijdige toetsing van een H0 wordt een Z-waarde gevonden van 1,72. Wat zal er met de H0 gebeuren als je toets bij een alfa van 5 %?
a) niet verwerpen, want de p-waarde zal kleiner zijn dan alfa
b) niet verwerpen, want de gevonden z-waarde is kleiner dan de kritieke z-waarde
c) zowel a als b
d) noch a, noch b
Ik heb opgezocht de kans die bij de Z-waarde 1,72 hoort; aflezen in tabel = 0.9564, dan
1 - 0.9564 = 0.0436. De significantie waarde is 0.05, 0,0436 is kleiner als de alfa van 5%, dus
H0 verwerpen lijkt me.. of maak ik hier een denkfout?
Het antwoord is namelijk B.. dan heb ik nog een vraag; hoe kan je weten aan de hand van deze gegevens dat de z-waarde kleiner is dan de kritieke z-waarde?
Geldt eigenlijk precies hetzelfde verhaal bij deze vraag:
6. Bij een rechtzijdige toetsing van een H0 wordt een Z-waarde gevonden van 1,84. Wat zal er met de H0 gebeuren als je toets bij een alfa van 1 %?
a) niet verwerpen, want de p-waarde zal kleiner zijn dan alfa
b) niet verwerpen, want de gevonden z-waarde is kleiner dan de kritieke z-waarde
c) zowel a als b
d) noch a, noch b
Z waarde is hierbij 0.9664 --> 1 - 0.9664 = 0.0336
Wie o wie kan mij helpen???
5. Bij een tweezijdige toetsing van een H0 wordt een Z-waarde gevonden van 1,72. Wat zal er met de H0 gebeuren als je toets bij een alfa van 5 %?
a) niet verwerpen, want de p-waarde zal kleiner zijn dan alfa
b) niet verwerpen, want de gevonden z-waarde is kleiner dan de kritieke z-waarde
c) zowel a als b
d) noch a, noch b
Ik heb opgezocht de kans die bij de Z-waarde 1,72 hoort; aflezen in tabel = 0.9564, dan
1 - 0.9564 = 0.0436. De significantie waarde is 0.05, 0,0436 is kleiner als de alfa van 5%, dus
H0 verwerpen lijkt me.. of maak ik hier een denkfout?
Het antwoord is namelijk B.. dan heb ik nog een vraag; hoe kan je weten aan de hand van deze gegevens dat de z-waarde kleiner is dan de kritieke z-waarde?
Geldt eigenlijk precies hetzelfde verhaal bij deze vraag:
6. Bij een rechtzijdige toetsing van een H0 wordt een Z-waarde gevonden van 1,84. Wat zal er met de H0 gebeuren als je toets bij een alfa van 1 %?
a) niet verwerpen, want de p-waarde zal kleiner zijn dan alfa
b) niet verwerpen, want de gevonden z-waarde is kleiner dan de kritieke z-waarde
c) zowel a als b
d) noch a, noch b
Z waarde is hierbij 0.9664 --> 1 - 0.9664 = 0.0336
Wie o wie kan mij helpen???


Er is een verschil tussen een tweezijdige en een enkelzijdige toetsing.
Bij een tweezijdige toetsing kan je z verwerpen als het > 1.96 of <-1.96 is. Bij een enkelzijdig toetsing mag je z verwerpen als het > 1.645 of < -1.645 bij een alfa van 0.05.
Zoek de formules op in de slides of in je boek.
B is inderdaad correct.
Bij een tweezijdige toetsing kan je z verwerpen als het > 1.96 of <-1.96 is. Bij een enkelzijdig toetsing mag je z verwerpen als het > 1.645 of < -1.645 bij een alfa van 0.05.
Zoek de formules op in de slides of in je boek.
B is inderdaad correct.


"Z-waarde is (in absolute waarde) kleiner dan de kritieke z-waarde" en "p-waarde is groter dan alfa" zijn hier equivalente uitspraken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Bedankt Zoem en Hattricker. Ik zal er vanaaf weer naar kijken.
x
x
"Vanity, definitely my favorite sin. . . ."


Ik heb een bepaalde functie sqrt ( xa + yb) , x,y>0 Hiervan moet ik aan de hand van de definietheid v/d hessian bepalen voor welke a,b (in R2) deze functie convex dan wel concaaf is. Hessian is te bepalen, dat zijn de 2e orde partiele afgeleiden. Deze zijn makkelijk te bepalen met mathematica.
Voor: strict convex moet gelden dat: hessian positief definiet
convex H pos. semidef
Concaaf/strict concaaf evenzo maar dan negatief
Om nu verder te kijken voor welke a & b alle entries groter/gelijk 0 zijn voor positief semidefiniet, respectievelijk kleiner/gelijk 0 voor negatief semidefiniet, lukt me niet. De 2e orde partiele afgeleiden zijn vrij gecompliceerde functies, waar mathematica zo geen raad mee weet. Iemand een tip hoe verder te gaan?
Voor: strict convex moet gelden dat: hessian positief definiet
convex H pos. semidef
Concaaf/strict concaaf evenzo maar dan negatief
Om nu verder te kijken voor welke a & b alle entries groter/gelijk 0 zijn voor positief semidefiniet, respectievelijk kleiner/gelijk 0 voor negatief semidefiniet, lukt me niet. De 2e orde partiele afgeleiden zijn vrij gecompliceerde functies, waar mathematica zo geen raad mee weet. Iemand een tip hoe verder te gaan?


Zo lastig is het niet. De dubbele afgeleide naar a is positief als
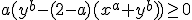
De determinant van de Hessiaan is positief als
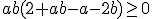
Dit kun je makkelijk zelf controleren door te gebruiken dat
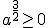
voor elke a. Bij de Hessiaan kun je ook nog een factor
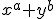
herkennen.
De determinant van de Hessiaan is positief als
Dit kun je makkelijk zelf controleren door te gebruiken dat
voor elke a. Bij de Hessiaan kun je ook nog een factor
herkennen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

