[Bèta wiskunde] Huiswerk- en vragentopic

donderdag 12 januari 2012 @ 14:51:01 #26

Tauchmeister

Ik moet y vrijmaken uit p-(15y^2-80y+96)=0.

p-(15y^2-80y+96)=0
p=(15y^2-80y+96)

Wanneer ik de abc-formule gebruik kom ik uit op D=(-80)^2-(4*15*96)=640. In het dictaat gaat men echter uit van een discriminant van 640+60. Waar komt die 60 vandaan?

[ Bericht 2% gewijzigd door Tauchmeister op 12-01-2012 15:07:57 ]

donderdag 12 januari 2012 @ 14:53:47 #27

Haushofer

quote:
Op donderdag 12 januari 2012 14:51 schreef Tauchmeister het volgende:
Ik moet y vrijmaken uit p-(15y^2-80y+96)=0.

p-(15y^2+80y-96)=0
p=(15y^2+80y-96)

Wanneer ik de abc-formule gebruik kom ik uit op D=(-80)^2-(4*15*96)=640. In het dictaat gaat men echter uit van een discriminant van 640+60. Waar komt die 60 vandaan?

Wat heb je met je p gedaan?

Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071

donderdag 12 januari 2012 @ 14:57:23 #28

bloodysunday

quote:
Op donderdag 12 januari 2012 14:40 schreef zoem het volgende:
Ken je de kettingregel? Want die moet je hier gebruiken.

$f'(x) = \frac{df(x)}{dx}=\frac{df(x)}{du} \cdot \frac{du}{dx}$

Ja die ken ik volgens mij moet het goed zijn op die manier, tenminste als ik naar het antwoord uit het boek kijk.

AJAX AMSTERDAM!

donderdag 12 januari 2012 @ 14:58:18 #29

Tauchmeister

quote:
Op donderdag 12 januari 2012 14:53 schreef Haushofer het volgende:

[..]

Wat heb je met je p gedaan?

Eigenlijk niets nu ik het zo bekijk. In het dictaat verdwijnt deze echter ook en wordt het y(p)=8/3±1/30*(640+60)^0,5. Daar kom ik ook op uit, op die 60 na in de discriminant.

donderdag 12 januari 2012 @ 15:04:11 #30

Haushofer

quote:
Op donderdag 12 januari 2012 14:58 schreef Tauchmeister het volgende:

[..]

Eigenlijk niets nu ik het zo bekijk. In het dictaat verdwijnt deze echter ook en wordt het y(p)=8/3±1/30*(640+60)^0,5. Daar kom ik ook op uit, op die 60 na in de discriminant.

Ik heb de vgl

$15y^2 + 80y - 96 - p \equiv Ay^2 + By + C = 0$

De discriminant is dan

$D = B^2 - 4 AC = 80^2 - 4*15*(96-p)$

De oplossing voor y wordt dan

$y(p) = \frac{-80 \pm \sqrt{D(p)}}{30}$

Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071

donderdag 12 januari 2012 @ 15:13:03 #31

Tauchmeister

Dus in het dictaat zijn ze vergeten om een p achter die 60 te zetten? Dan is de discriminant dus 640+60p.

donderdag 12 januari 2012 @ 15:15:36 #32

Haushofer

quote:
Op donderdag 12 januari 2012 15:13 schreef Tauchmeister het volgende:
Dus in het dictaat zijn ze vergeten om een p achter die 60 te zetten? Dan is de discriminant dus 640+60p.

Die discriminant moet iig een p bevatten

Je hebt immers (met mijn notatie) dat C = -(96+p).

Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071

donderdag 12 januari 2012 @ 15:16:36 #33

Tauchmeister

Thanks.

donderdag 12 januari 2012 @ 21:44:23 #34

Sir_Windsor

Ik heb het volgende in R geschreven om een CDF van een compound poisson distributie te schatten met behulp van simulatie.
N<-rpois(1000,5)
X=(1:1000)
for (i in 1:1000){
x=sample(1:6, N[i], repl=T, prob=c(1,1,1,2,2,3))
X[i]=sum(x)}

Nu wil ik alleen graag van X weten hoe vaak elke waarde voorkomt. Iemand enig idee?

zondag 15 januari 2012 @ 17:40:52 #35

thenxero

[ Bericht 53% gewijzigd door thenxero op 16-01-2012 18:19:17 ]

zondag 15 januari 2012 @ 20:40:52 #36

Oneironaut

Gewone differentiaalvergelijking, homogeen met complexe eigenwaarden
Ik heb het volgende beginwaardeprobleem:
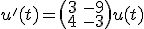
$u'(t)=\begin{pmatrix} 3 & -9 \\ 4 & -3 \end{pmatrix} u(t)$
$u(0)=\begin{pmatrix} 2 & \\-4&\end{pmatrix}$

Een zeker oplossing is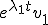 $e^{\lambda_1 t}v_1$
Met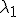 $\lambda_1$ is de eigenwaarde van de bovenstaande matrix en 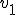$v_1$ de bijbehorende eigenvector.

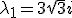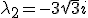Ok. Ik bereken de eigenwaarden... die blijken $\lambda_1=3\sqrt{3}i$ en $\lambda_2=-3\sqrt{3}i$ (de compl. geconjugeerde).

De bijbehorende (eerste) eigenvector is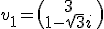 $v_1=\begin{pmatrix} 3 & \\1-sqrt{3}i&\end{pmatrix}$

Tot zover alles goed. Gechecked en klopt. Maar nu wil ik dus de algemene oplossing opschrijven.
En tref ik twee verschillende uitleggen aan.

• Mijn dictaat zegt:
De algemene oplossing wordt nu gegeven door:
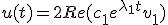$u(t)=2Re(c_1 e^{\lambda_1t}v_1)$ omdat zowel de eigenwaarden, eigenvectoren als factoren complex geconjugeerden van elkaar zijn.

• Maar een ander dictaat zegt (en dit snap ik dus wel):
de algemene oplossing wordt gegeven door:
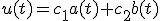
$u(t)=c_1 a(t)+c_2 b(t)$
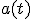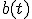Waarbij $a(t)$ en $b(t)$ volgen door je eerste specifieke oplossing te schrijven als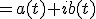 $=a(t)+ib(t)$

Vervolgens haal je uit de beginconditie de constanten.

• Met het andere dictaat kom ik op het antwoord dat ook wolframalpha onderschrijft:
klik

• Maar met eigen dictaat kom je op:

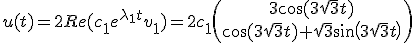
$u(t)=2Re(c_1 e^{\lambda_1t}v_1)=2 c_1 \begin{pmatrix} 3\cos(3\sqrt{3}t) & \\ \cos(3\sqrt{3}t)+\sqrt{3}sin(3\sqrt{3}t)&\end{pmatrix}$
En dat lijkt toch niet hetzelfde te zijn....

Dus mijn vraag is klopt het onderstreepte uit mijn dictaat? En zo ja, leveren beide aanpakken dan dus wel hetzelfde antwoord op?

[ Bericht 0% gewijzigd door Oneironaut op 15-01-2012 20:48:13 ]

zondag 15 januari 2012 @ 20:51:32 #37

thabit

quote:
Op zondag 15 januari 2012 20:40 schreef Oneironaut het volgende:
$u(t)=2Re(c_1 e^{\lambda_1t}v_1)=2 c_1 \begin{pmatrix} 3\cos(3\sqrt{3}t) & \\ \cos(3\sqrt{3}t)+\sqrt{3}sin(3\sqrt{3}t)&\end{pmatrix}$

Je gaat er hier van uit dat c₁ reëel is, maar dat hoeft niet.

zondag 15 januari 2012 @ 20:54:12 #38

Oneironaut

quote:
Op zondag 15 januari 2012 20:51 schreef thabit het volgende:

[..]

Je gaat er hier van uit dat c₁ reëel is, maar dat hoeft niet.

Ah verhip. Als ik dus nu uit mijn specifieke eerste oplossing m.b.v. de begincondities c₁ afleid en dan vervolgens die regel uit het dictaat toepas zou er hetzelfde moeten uitkomen?
Bedankt voor je snelle antwoord

zondag 15 januari 2012 @ 20:56:54 #39

Oneironaut

Nee wacht hoe kom ik nu aan c1?

maandag 16 januari 2012 @ 22:34:37 #40

thenxero

Laat {N(t), t>0} een Poisson proces zijn met parameter k. Bereken E(N(4) - N(2) | N(1)=3).

Ik heb twee manieren bedacht, maar ze geven verschillende antwoorden. Wat gaat er fout?

E(N(4) - N(2) | N(1)=3)
= E(N(3) - N(1) | N(1)=3) (vanwege "stationarity")
= E(N(3) - 3)
= 3k -3

E(N(4) - N(2) | N(1)=3)
=E(N(4) - N(2)) (vanwege "independent increments")
=E(N(2) - N(0)) (vanwege stationarity)
=E(N(2))
=2k

maandag 16 januari 2012 @ 23:17:28 #41

twaalf

quote:
Op maandag 16 januari 2012 22:34 schreef thenxero het volgende:
= E(N(3) - N(1) | N(1)=3) (vanwege "stationarity")
= E(N(3) - 3)

Dit klopt niet want N(3) | N(1)=3 heeft een andere verdeling dan N(3).

maandag 16 januari 2012 @ 23:32:01 #42

thenxero

Ah, dus
E(N(4) - N(2) | N(1)=3)
= E(N(3) - N(1) | N(1)=3)
= E(N(3) | N(1) = 3) - 3
= E(N(2)) + 3 - 3
= 2k

En dan klopt het weer. Thanks.

woensdag 18 januari 2012 @ 17:40:40 #43

Anoonumos

Is er iemand die me op weg kan hen helpen met deze vraag over continuiteit?

[ Bericht 22% gewijzigd door Anoonumos op 18-01-2012 18:01:07 ]

woensdag 18 januari 2012 @ 18:54:59 #44

Physics

Let niet op wat na = teken staat, ik heb het even in wolfram ingetypt zodat ik niet met LaTeX hoefde te kloten

Evalueer gif&s=39&w=480&h=39

over gebied D met D={(x,y)| |x|+|y|=<1}

(1) Ondergrens x en y zijn als |x| of |y| minimaal zijn voor |x|+|y|<=1, dat is voor x,y=-1 als y,x=0
(2) Bovengrens x en y zijn als |x| of |y| maximaal zijn voor |x|+|y|<=1, dat is voor x,y=1 als y,x=0
(3) Dus integreren naar x en y met beide grenzen van -1 naar 1

Klopt mijn gedachtegang??

woensdag 18 januari 2012 @ 19:56:45 #45

twaalf

quote:
Op woensdag 18 januari 2012 18:54 schreef Physics het volgende:
Let niet op wat na = teken staat, ik heb het even in wolfram ingetypt zodat ik niet met LaTeX hoefde te kloten

Evalueer [ afbeelding ] over gebied D met D={(x,y)| |x|+|y|=<1}

(1) Ondergrens x en y zijn als |x| of |y| minimaal zijn voor |x|+|y|<=1, dat is voor x,y=-1 als y,x=0
(2) Bovengrens x en y zijn als |x| of |y| maximaal zijn voor |x|+|y|<=1, dat is voor x,y=1 als y,x=0
(3) Dus integreren naar x en y met beide grenzen van -1 naar 1

Klopt mijn gedachtegang??

Gewoon even een plaatje tekenen hoe gebied D eruit ziet. Je krijgt dan een gebied dat wordt afgebakend door de vier lijnen |y|=1-|x|. Ja dat zijn vier lijnen, want |y|=+-y, |x|=+-x.

woensdag 18 januari 2012 @ 19:57:12 #46

twaalf

Geen plaatjes kopiëren van Wolfram, want die zijn binnen een uur weer verdwenen van hun server.

woensdag 18 januari 2012 @ 20:10:11 #47

twaalf

quote:
Op woensdag 18 januari 2012 17:40 schreef Anoonumos het volgende:
Is er iemand die me op weg kan hen helpen met deze vraag over continuiteit?
[ afbeelding ]

Voor de x die de inversen zijn van een natuurlijk getal, is het bewijs makkelijk. Maar als je een x hebt die bijvoorbeeld ligt in het interval $\left[\frac{1}{n+1},\frac{1}{n}\right]$ ligt, staat er niets over convergentie. In de limiet gaat de lengte van dit interval naar nul, dus kun je dan bewijzen dat $|x-f(1/n)|$ kleiner is dan een zekere $\varepsilon$ . Als je het voor beide soorten x hebt bewezen, heb je het voor het gehele interval $[0,\delta]$ bewezen.

woensdag 18 januari 2012 @ 21:00:34 #48

slacKard.x

gek op meisjes met bruine ogen

Goedenavond FOK!ers.

Ik snap deze vragen niet, eerst lukte het aardig maar ik ben het na de kerstvakantie weer helemaal kwijtgeraakt

Ik heb de blaadjes even gescanned.

http://img52.imageshack.us/img52/29/17012012443copycopy.jpg (copy/paste deze link)
http://img688.imageshack.us/img688/2536/17012012445copy.jpg (copy/paste deze link)

Groeten SlacKard

we cant feed the poor but we can fund a war

woensdag 18 januari 2012 @ 21:02:14 #49

twaalf

Nog een vraag in het bijzonder want ik ga niet 8 vragen voormaken?

woensdag 18 januari 2012 @ 21:05:47 #50

slacKard.x

gek op meisjes met bruine ogen

Vraag 1.

we cant feed the poor but we can fund a war

Forum Opties
Forumhop:
Hop naar:	(afkorting, bv 'KLB')

» school, studie en onderwijs

» school, studie en onderwijs