SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP


quote:Op maandag 2 januari 2012 13:38 schreef Warren het volgende:
Kan iemand misschien toelichten waarom
| x + a | < b = -b < x + a <b ?
In mijn boek wordt dit als "regel" gegeven, maar ik wil het ook snappen.
| x + a | = b kan worden opgelost door
x + a = b en x + a = - b op te lossen. Ik dacht dus ook dit toe te passen op | x + a | < b. Kortom:
x + a < b en x + a < - b op te lossen. Maar hier kom ik niet op het juiste antwoord, omdat dat het ingelijkheidsteken bij beide dezelfde kant op wijst.
Bij voorbaat dank.
quote:Op maandag 2 januari 2012 13:55 schreef freiss het volgende:
[..]
Je regel om |x+a|=b op te lossen is niet helemaal goed, je moet namelijk dan x+a=b en -(x+a)=b oplossen. Bij het gelijkheidsteken maakt dat niet uit, maar bij het >-teken klapt het teken om bij vermenigvuldiging met een negatief getal. Dan kom je wel op het goede antwoord.
quote:Op maandag 2 januari 2012 13:55 schreef zoem het volgende:
Je vergeet het teken om te draaien bij minus b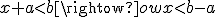
en


Zou iemand kunnen toelichten wat hier precies gebeurt?
Uit een oud studieboek, er staat verder geen toelichting bij
Het staat na een hoofdstuk over grootste gemene delers en kleinste gemene veelvouden... Ik zie wel dat 8 de grootste gemene deler van 16 en 24 is, en 3 van 24 en 9, en 4 van 32, 24 en 16, maar wat ze nou precies doen is me nog onduidelijk.
[ Bericht 22% gewijzigd door kutkloon7 op 03-01-2012 01:06:40 ]


Het komt uit http://ia600306.us.archiv(...)elemen00carrrich.pdf (pagina 37), maar daar staat ook geen uitleg bij 
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Met http://nl.wikipedia.org/wiki/Worteltrekken kom ik op dit onvolledige verhaaltje:
Je begint van rechts met het maken van groepjes van 2 coefficienten. De 16 blijft los over. 16 is een kwadraat, dus daar komt de 4 in het antwoord van.
Dan het volgende groepje van 2: -24+41.
De voorlopige wortel is 4, twee maar vier is die 8 die links staat*. -24/8 = -3 rest 0.
Dan trek je van -24+41 de 8*(-3) + 3^2 af, houd je de 32 over. Pak je er weer een groepje van twee getallen bij.
thabit komt morgen vertellen hoe het verder gaat
*het voorlopige antwoord is 4a+b, waarbij a is zoals in de opgave en b wat we verder nog zoeken. (4a+b)² = 16a²+8ab+b². Die 24 is de 8b, dus b=-3.
[ Bericht 10% gewijzigd door GlowMouse op 03-01-2012 02:39:13 ]
Je begint van rechts met het maken van groepjes van 2 coefficienten. De 16 blijft los over. 16 is een kwadraat, dus daar komt de 4 in het antwoord van.
Dan het volgende groepje van 2: -24+41.
De voorlopige wortel is 4, twee maar vier is die 8 die links staat*. -24/8 = -3 rest 0.
Dan trek je van -24+41 de 8*(-3) + 3^2 af, houd je de 32 over. Pak je er weer een groepje van twee getallen bij.
thabit komt morgen vertellen hoe het verder gaat
*het voorlopige antwoord is 4a+b, waarbij a is zoals in de opgave en b wat we verder nog zoeken. (4a+b)² = 16a²+8ab+b². Die 24 is de 8b, dus b=-3.
[ Bericht 10% gewijzigd door GlowMouse op 03-01-2012 02:39:13 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Volgens mij snap ik het. Ze zoeken eerst een x en y zodat
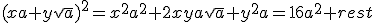
Dan is x natuurlijk 4, dan zoeken we y zodat
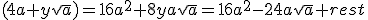
Dus y = -3
Dan heb je:
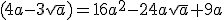
En dan haal je die 9 van de 41 af, en hou je 32 over. Dan doen ze:
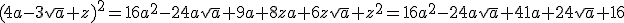
dus kan je alleen al uit die z2 = 16 concluderen dat z 4 moet zijn (en dan moet je natuurlijk wel controleren of z = 4 wel het gewenste resultaat oplevert als je hem invult in de middelste formule, anders is er geen mooie wortel).
Ok, dit is geloof ik niet echt wat ze daar doen, maar voor mij werkt het .
.
En nu moet ik leren, ik kijk er misschien vanavond of morgen nog een keer naar, want nu snap ik er niks meer van als ik naar die methode van het plaatje kijk . Dank voor de hulp!
. Dank voor de hulp!
Edit: ik had natuurlijk net zo goed in één keer:
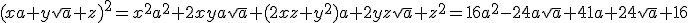
kunnen stellen, en dan kunnen concluderen dat x = 4 (want x2 moet 16 zijn), dan dat y = -3 (want 2xy = 8y = -24), en dan z = 4 (want z2 = 16)
(nu ben ik de mogelijkheden x = -4 en z = -4 vergeten, als je deze neemt krijg je gewoon de negatieve polynoom, wat in het kwadraat ook 16a2 - 24aa + 41a + 24 a + 16) is, maar geen wortel omdat deze negatief is)
[ Bericht 17% gewijzigd door kutkloon7 op 03-01-2012 12:30:15 ]
Dan is x natuurlijk 4, dan zoeken we y zodat
Dus y = -3
Dan heb je:
En dan haal je die 9 van de 41 af, en hou je 32 over. Dan doen ze:
dus kan je alleen al uit die z2 = 16 concluderen dat z 4 moet zijn (en dan moet je natuurlijk wel controleren of z = 4 wel het gewenste resultaat oplevert als je hem invult in de middelste formule, anders is er geen mooie wortel).
Ok, dit is geloof ik niet echt wat ze daar doen, maar voor mij werkt het
En nu moet ik leren, ik kijk er misschien vanavond of morgen nog een keer naar, want nu snap ik er niks meer van als ik naar die methode van het plaatje kijk
Edit: ik had natuurlijk net zo goed in één keer:
kunnen stellen, en dan kunnen concluderen dat x = 4 (want x2 moet 16 zijn), dan dat y = -3 (want 2xy = 8y = -24), en dan z = 4 (want z2 = 16)
(nu ben ik de mogelijkheden x = -4 en z = -4 vergeten, als je deze neemt krijg je gewoon de negatieve polynoom, wat in het kwadraat ook 16a2 - 24aa + 41a + 24 a + 16) is, maar geen wortel omdat deze negatief is)
[ Bericht 17% gewijzigd door kutkloon7 op 03-01-2012 12:30:15 ]


Waarom moet je dit weten?
Check hier de laatste pagina, waarom het werkt.
http://www.rightbase.nl/Worteltrekken_met_pen_en_papier.pdf
Check hier de laatste pagina, waarom het werkt.
http://www.rightbase.nl/Worteltrekken_met_pen_en_papier.pdf


Eh, algemene interessequote:Op dinsdag 3 januari 2012 12:23 schreef thenxero het volgende:
Waarom moet je dit weten?
Check hier de laatste pagina, waarom het werkt.
http://www.rightbase.nl/Worteltrekken_met_pen_en_papier.pdf
Dat lijkt inderdaad de methode te zijn die ze daar ook gebruiken, thanks
[ Bericht 3% gewijzigd door kutkloon7 op 03-01-2012 12:37:44 ]


Ik weet niet goed waar ik dit moet plaatsen, en aangezien het voor een vak wiskunde en financiële rekenkunde is plaatst ik het hier..
Een studente moet aan het einde van iedere half jaar 12 gelijke termijnen van ¤500,- betalen aan een bank. S.I. = 8 % per jaar. De eerste termijn moet betaald worden op 31 december 2008.
De in financiële nood geraakte studente wil na betaling van de eerste 2 termijnen de betaling van de overige 10 termijnen met 1 jaar uitstellen: dit betekent dat de studente op 31 december 2010 het derde termijnbedrag zal betalen, op 30 juni 2011 zal zij het vierde termijnbedrag betalen..etc.
b1) Hoe groot is de resterende restschuld van de studente op 1 juli 2009 direct na betaling van de tweede termijn?
Mijn antwoord is:
R = Ann [ 1/1.0392 .... + 1/1.0392^10]
Som meetkundige rij = 8.1433
Nu heb ik als antwoord 500 * 8.1433 = 4017.65 euro, maar de '500' klopt in dit geval niet.
Hieronder een voorbeeld uit het boek:
Ik snap dan ook niet hoe ze hier aan de 37.488,80 komen.
Een studente moet aan het einde van iedere half jaar 12 gelijke termijnen van ¤500,- betalen aan een bank. S.I. = 8 % per jaar. De eerste termijn moet betaald worden op 31 december 2008.
De in financiële nood geraakte studente wil na betaling van de eerste 2 termijnen de betaling van de overige 10 termijnen met 1 jaar uitstellen: dit betekent dat de studente op 31 december 2010 het derde termijnbedrag zal betalen, op 30 juni 2011 zal zij het vierde termijnbedrag betalen..etc.
b1) Hoe groot is de resterende restschuld van de studente op 1 juli 2009 direct na betaling van de tweede termijn?
Mijn antwoord is:
R = Ann [ 1/1.0392 .... + 1/1.0392^10]
Som meetkundige rij = 8.1433
Nu heb ik als antwoord 500 * 8.1433 = 4017.65 euro, maar de '500' klopt in dit geval niet.
Hieronder een voorbeeld uit het boek:
Ik snap dan ook niet hoe ze hier aan de 37.488,80 komen.


In het voorbeeld: je kunt niet 200.000 door 8 delen, want er komt ook nog rente bij. Om die 37.488 uit te rekenen, moet je ook weer gebruik maken van een meetkundige rij. Daar staat vast ook wel een voorbeeldje van in je boek, anders kun je het uitschrijven.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik heb een vraag.
Ik heb slakkenhuisjes gemeten op een aantal punten en daar ook ratio's tussen genomen.
Nou wil ik weten of de verschillen die er tussen de verschillende populaties zijn veroorzaakt worden door ecologische parameters (regenval, temperatuur, hoogte).
Een vriend raadde mij een covariantie matrix aan, maar hij is nu op vakantie en kan me daar niet mee helpen.
Wat zeggen de cijfers in zo'n matrix precies?
Ik heb slakkenhuisjes gemeten op een aantal punten en daar ook ratio's tussen genomen.
Nou wil ik weten of de verschillen die er tussen de verschillende populaties zijn veroorzaakt worden door ecologische parameters (regenval, temperatuur, hoogte).
Een vriend raadde mij een covariantie matrix aan, maar hij is nu op vakantie en kan me daar niet mee helpen.
Wat zeggen de cijfers in zo'n matrix precies?
Emotionele exclusiviteit monogamie-adept


Je kunt geen oorzaken bepalen aan de hand van het door jou uitgevoerde onderzoek.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik begrijp dat je niet met zekerheid kunt zeggen dat iets daardoor veroorzaakt wordt.quote:Op zondag 8 januari 2012 23:53 schreef GlowMouse het volgende:
Je kunt geen oorzaken bepalen aan de hand van het door jou uitgevoerde onderzoek.
Maar stel dat ik wil zien of er een verband bestaat tussen bijvoorbeeld grootte van de schelp en hoogte van vindplaats. Hoe kan ik dit dan aanpakken?
Ik weet helaas vrij weinig van statistiek, dus alvast mijn excuses als ik hier dom overkom.
Emotionele exclusiviteit monogamie-adept


Dat gaat met een statistische toets. Iemand met kennis van regressie zou je hierbij kunnen helpen, misschien ken je iemand aan een sociale of economische faculteit want het is lastig om hier allemaal neer te zetten.quote:Op zondag 8 januari 2012 23:56 schreef Kaneelstokje het volgende:
[..]
Ik begrijp dat je niet met zekerheid kunt zeggen dat iets daardoor veroorzaakt wordt.
Maar stel dat ik wil zien of er een verband bestaat tussen bijvoorbeeld grootte van de schelp en hoogte van vindplaats. Hoe kan ik dit dan aanpakken?
Ik weet helaas vrij weinig van statistiek, dus alvast mijn excuses als ik hier dom overkom.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Schrijf deze functie als
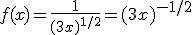

Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


En dan kun je dat nog mooier opschrijven.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


ja tegen die stap loop ik aanquote:Op donderdag 12 januari 2012 14:18 schreef GlowMouse het volgende:
En dan kun je dat nog mooier opschrijven.
AJAX AMSTERDAM!


Je krijgt
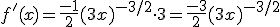
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Ik moet y vrijmaken uit p-(15y^2-80y+96)=0.
p-(15y^2-80y+96)=0
p=(15y^2-80y+96)
Wanneer ik de abc-formule gebruik kom ik uit op D=(-80)^2-(4*15*96)=640. In het dictaat gaat men echter uit van een discriminant van 640+60. Waar komt die 60 vandaan?
[ Bericht 2% gewijzigd door Tauchmeister op 12-01-2012 15:07:57 ]
p-(15y^2-80y+96)=0
p=(15y^2-80y+96)
Wanneer ik de abc-formule gebruik kom ik uit op D=(-80)^2-(4*15*96)=640. In het dictaat gaat men echter uit van een discriminant van 640+60. Waar komt die 60 vandaan?
[ Bericht 2% gewijzigd door Tauchmeister op 12-01-2012 15:07:57 ]


Wat heb je met je p gedaan?quote:Op donderdag 12 januari 2012 14:51 schreef Tauchmeister het volgende:
Ik moet y vrijmaken uit p-(15y^2-80y+96)=0.
p-(15y^2+80y-96)=0
p=(15y^2+80y-96)
Wanneer ik de abc-formule gebruik kom ik uit op D=(-80)^2-(4*15*96)=640. In het dictaat gaat men echter uit van een discriminant van 640+60. Waar komt die 60 vandaan?
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Ja die ken ik volgens mij moet het goed zijn op die manier, tenminste als ik naar het antwoord uit het boek kijk.quote:Op donderdag 12 januari 2012 14:40 schreef zoem het volgende:
Ken je de kettingregel? Want die moet je hier gebruiken.
AJAX AMSTERDAM!


Eigenlijk niets nu ik het zo bekijk. In het dictaat verdwijnt deze echter ook en wordt het y(p)=8/3±1/30*(640+60)^0,5. Daar kom ik ook op uit, op die 60 na in de discriminant.quote:


Ik heb de vglquote:Op donderdag 12 januari 2012 14:58 schreef Tauchmeister het volgende:
[..]
Eigenlijk niets nu ik het zo bekijk. In het dictaat verdwijnt deze echter ook en wordt het y(p)=8/3±1/30*(640+60)^0,5. Daar kom ik ook op uit, op die 60 na in de discriminant.
De discriminant is dan
De oplossing voor y wordt dan
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Dus in het dictaat zijn ze vergeten om een p achter die 60 te zetten? Dan is de discriminant dus 640+60p.


Die discriminant moet iig een p bevattenquote:Op donderdag 12 januari 2012 15:13 schreef Tauchmeister het volgende:
Dus in het dictaat zijn ze vergeten om een p achter die 60 te zetten? Dan is de discriminant dus 640+60p.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Ik heb het volgende in R geschreven om een CDF van een compound poisson distributie te schatten met behulp van simulatie.
N<-rpois(1000,5)
X=(1:1000)
for (i in 1:1000){
x=sample(1:6, N[i], repl=T, prob=c(1,1,1,2,2,3))
X[i]=sum(x)}
Nu wil ik alleen graag van X weten hoe vaak elke waarde voorkomt. Iemand enig idee?
N<-rpois(1000,5)
X=(1:1000)
for (i in 1:1000){
x=sample(1:6, N[i], repl=T, prob=c(1,1,1,2,2,3))
X[i]=sum(x)}
Nu wil ik alleen graag van X weten hoe vaak elke waarde voorkomt. Iemand enig idee?


Gewone differentiaalvergelijking, homogeen met complexe eigenwaarden
Ik heb het volgende beginwaardeprobleem:
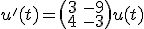

Een zeker oplossing is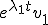
Met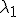 is de eigenwaarde van de bovenstaande matrix en
is de eigenwaarde van de bovenstaande matrix en 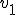 de bijbehorende eigenvector.
de bijbehorende eigenvector.
Ok. Ik bereken de eigenwaarden... die blijken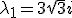 en
en 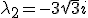 (de compl. geconjugeerde).
(de compl. geconjugeerde).
De bijbehorende (eerste) eigenvector is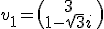
Tot zover alles goed. Gechecked en klopt. Maar nu wil ik dus de algemene oplossing opschrijven.
En tref ik twee verschillende uitleggen aan.
• Mijn dictaat zegt:
De algemene oplossing wordt nu gegeven door:
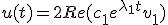 omdat zowel de eigenwaarden, eigenvectoren als factoren complex geconjugeerden van elkaar zijn.
omdat zowel de eigenwaarden, eigenvectoren als factoren complex geconjugeerden van elkaar zijn.
• Maar een ander dictaat zegt (en dit snap ik dus wel):
de algemene oplossing wordt gegeven door:
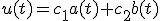
Waarbij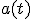 en
en 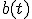 volgen door je eerste specifieke oplossing te schrijven als
volgen door je eerste specifieke oplossing te schrijven als 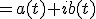
Vervolgens haal je uit de beginconditie de constanten.
• Met het andere dictaat kom ik op het antwoord dat ook wolframalpha onderschrijft:
klik
• Maar met eigen dictaat kom je op:
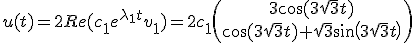
En dat lijkt toch niet hetzelfde te zijn....
Dus mijn vraag is klopt het onderstreepte uit mijn dictaat? En zo ja, leveren beide aanpakken dan dus wel hetzelfde antwoord op?
[ Bericht 0% gewijzigd door Oneironaut op 15-01-2012 20:48:13 ]
Ik heb het volgende beginwaardeprobleem:
Een zeker oplossing is
Met
Ok. Ik bereken de eigenwaarden... die blijken
De bijbehorende (eerste) eigenvector is
Tot zover alles goed. Gechecked en klopt. Maar nu wil ik dus de algemene oplossing opschrijven.
En tref ik twee verschillende uitleggen aan.
• Mijn dictaat zegt:
De algemene oplossing wordt nu gegeven door:
• Maar een ander dictaat zegt (en dit snap ik dus wel):
de algemene oplossing wordt gegeven door:
Waarbij
Vervolgens haal je uit de beginconditie de constanten.
• Met het andere dictaat kom ik op het antwoord dat ook wolframalpha onderschrijft:
klik
• Maar met eigen dictaat kom je op:
En dat lijkt toch niet hetzelfde te zijn....
Dus mijn vraag is klopt het onderstreepte uit mijn dictaat? En zo ja, leveren beide aanpakken dan dus wel hetzelfde antwoord op?
[ Bericht 0% gewijzigd door Oneironaut op 15-01-2012 20:48:13 ]


Ah verhip. Als ik dus nu uit mijn specifieke eerste oplossing m.b.v. de begincondities c1 afleid en dan vervolgens die regel uit het dictaat toepas zou er hetzelfde moeten uitkomen?quote:Op zondag 15 januari 2012 20:51 schreef thabit het volgende:
[..]
Je gaat er hier van uit dat c1 reëel is, maar dat hoeft niet.
Bedankt voor je snelle antwoord


Laat {N(t), t>0} een Poisson proces zijn met parameter k. Bereken E(N(4) - N(2) | N(1)=3).
Ik heb twee manieren bedacht, maar ze geven verschillende antwoorden. Wat gaat er fout?
E(N(4) - N(2) | N(1)=3)
= E(N(3) - N(1) | N(1)=3) (vanwege "stationarity")
= E(N(3) - 3)
= 3k -3
E(N(4) - N(2) | N(1)=3)
=E(N(4) - N(2)) (vanwege "independent increments")
=E(N(2) - N(0)) (vanwege stationarity)
=E(N(2))
=2k
Ik heb twee manieren bedacht, maar ze geven verschillende antwoorden. Wat gaat er fout?
E(N(4) - N(2) | N(1)=3)
= E(N(3) - N(1) | N(1)=3) (vanwege "stationarity")
= E(N(3) - 3)
= 3k -3
E(N(4) - N(2) | N(1)=3)
=E(N(4) - N(2)) (vanwege "independent increments")
=E(N(2) - N(0)) (vanwege stationarity)
=E(N(2))
=2k


Dit klopt niet want N(3) | N(1)=3 heeft een andere verdeling dan N(3).quote:Op maandag 16 januari 2012 22:34 schreef thenxero het volgende:
= E(N(3) - N(1) | N(1)=3) (vanwege "stationarity")
= E(N(3) - 3)


Ah, dus
E(N(4) - N(2) | N(1)=3)
= E(N(3) - N(1) | N(1)=3)
= E(N(3) | N(1) = 3) - 3
= E(N(2)) + 3 - 3
= 2k
En dan klopt het weer. Thanks.
E(N(4) - N(2) | N(1)=3)
= E(N(3) - N(1) | N(1)=3)
= E(N(3) | N(1) = 3) - 3
= E(N(2)) + 3 - 3
= 2k
En dan klopt het weer. Thanks.


Is er iemand die me op weg kan hen helpen met deze vraag over continuiteit?
[ Bericht 22% gewijzigd door Anoonumos op 18-01-2012 18:01:07 ]
[ Bericht 22% gewijzigd door Anoonumos op 18-01-2012 18:01:07 ]


Let niet op wat na = teken staat, ik heb het even in wolfram ingetypt zodat ik niet met LaTeX hoefde te kloten 
Evalueer over gebied D met D={(x,y)| |x|+|y|=<1}
(1) Ondergrens x en y zijn als |x| of |y| minimaal zijn voor |x|+|y|<=1, dat is voor x,y=-1 als y,x=0
(2) Bovengrens x en y zijn als |x| of |y| maximaal zijn voor |x|+|y|<=1, dat is voor x,y=1 als y,x=0
(3) Dus integreren naar x en y met beide grenzen van -1 naar 1
Klopt mijn gedachtegang??
Evalueer over gebied D met D={(x,y)| |x|+|y|=<1}
(1) Ondergrens x en y zijn als |x| of |y| minimaal zijn voor |x|+|y|<=1, dat is voor x,y=-1 als y,x=0
(2) Bovengrens x en y zijn als |x| of |y| maximaal zijn voor |x|+|y|<=1, dat is voor x,y=1 als y,x=0
(3) Dus integreren naar x en y met beide grenzen van -1 naar 1
Klopt mijn gedachtegang??


Gewoon even een plaatje tekenen hoe gebied D eruit ziet. Je krijgt dan een gebied dat wordt afgebakend door de vier lijnen |y|=1-|x|. Ja dat zijn vier lijnen, want |y|=+-y, |x|=+-x.quote:Op woensdag 18 januari 2012 18:54 schreef Physics het volgende:
Let niet op wat na = teken staat, ik heb het even in wolfram ingetypt zodat ik niet met LaTeX hoefde te kloten
Evalueer [ afbeelding ] over gebied D met D={(x,y)| |x|+|y|=<1}
(1) Ondergrens x en y zijn als |x| of |y| minimaal zijn voor |x|+|y|<=1, dat is voor x,y=-1 als y,x=0
(2) Bovengrens x en y zijn als |x| of |y| maximaal zijn voor |x|+|y|<=1, dat is voor x,y=1 als y,x=0
(3) Dus integreren naar x en y met beide grenzen van -1 naar 1
Klopt mijn gedachtegang??


Voor de x die de inversen zijn van een natuurlijk getal, is het bewijs makkelijk. Maar als je een x hebt die bijvoorbeeld ligt in het intervalquote:Op woensdag 18 januari 2012 17:40 schreef Anoonumos het volgende:
Is er iemand die me op weg kan hen helpen met deze vraag over continuiteit?
[ afbeelding ]


Goedenavond FOK!ers.
Ik snap deze vragen niet, eerst lukte het aardig maar ik ben het na de kerstvakantie weer helemaal kwijtgeraakt
Ik heb de blaadjes even gescanned.
http://img52.imageshack.us/img52/29/17012012443copycopy.jpg (copy/paste deze link)
http://img688.imageshack.us/img688/2536/17012012445copy.jpg (copy/paste deze link)
Groeten SlacKard
Ik snap deze vragen niet, eerst lukte het aardig maar ik ben het na de kerstvakantie weer helemaal kwijtgeraakt
Ik heb de blaadjes even gescanned.
http://img52.imageshack.us/img52/29/17012012443copycopy.jpg (copy/paste deze link)
http://img688.imageshack.us/img688/2536/17012012445copy.jpg (copy/paste deze link)
Groeten SlacKard
we cant feed the poor but we can fund a war





 Op
Op 