[Bèta wiskunde] Huiswerk- en vragentopic

Index

» school, studie en onderwijs

actieve topics nieuwe topics
abonnement Unibet Coolblue Bitvavo
  dinsdag 21 februari 2012 @ 11:51:34 #221
256829 Sokz
Livin' the life
pi_108220011
En een constante 'C' ? :P
pi_108236476
Ach, zolang er geen verdere randvoorwaarden vermeldt staan lig ik daar niet wakker van :z . Foutieve domeinrestrictie daarintegen }:| ...
pi_108236673
wat is de nederlandse naam voor equation ookalweer? ben het ff helemaal kwijt :')
Winnaar KLB verkiezingen 2012.
pi_108236739
quote:
4s.gif Op dinsdag 21 februari 2012 20:05 schreef gogosweden het volgende:
wat is de nederlandse naam voor equation ookalweer? ben het ff helemaal kwijt :')
Vergelijking is denk ik wat het meest in de buurt komt. Google translate?
pi_108236781
quote:
2s.gif Op dinsdag 21 februari 2012 20:07 schreef kutkloon7 het volgende:

[..]

Vergelijking is denk ik wat het meest in de buurt komt. Google translate?
het klonk toch niet helemaal goed dus daarom vroeg ik het hier voor de zekerheid na :@
Winnaar KLB verkiezingen 2012.
pi_108237327
En in het Zweeds is het zeker førglaikin.
pi_108237495
ekvation
Winnaar KLB verkiezingen 2012.
pi_108237605
Cool, bijna zoals in het engels
pi_108238697
Ik wil de nde macht van een simpele matrix uitrekenen. Is er een manier voor? Mathematica komt er wel uuit, dus ik dacht dat het ook wel met de hand na te gaan moet zijn.
For the record, dit is de matrix:


En de nde macht van deze matrix is:


Oja, ik ken de manier waarbij je de matrix diagonaliseert, dat kan bij deze matrix niet omdat er geen basis van eigenvectoren is. Er is wel een matrix te maken zodat (als we de matrix met eigenvectoren als kolommen V noemen, de matrix waarvan ik de diagonaalmatrix wil hebben M en de diagonaalmatrix met eigenwaarden L):
MV = VL
Maar nu is v niet inverteerbaar, omdat zijn determinant 0 is.

[ Bericht 5% gewijzigd door motorbloempje op 12-08-2013 12:46:22 ]
pi_108239180
quote:
2s.gif Op dinsdag 21 februari 2012 20:45 schreef kutkloon7 het volgende:
Ik wil de nde macht van een simpele matrix uitrekenen. Is er een manier voor? Mathematica komt er wel uuit, dus ik dacht dat het ook wel met de hand na te gaan moet zijn.
For the record, dit is de matrix:
[ afbeelding ]

En de nde macht van deze matrix is:
[ afbeelding ]

Oja, ik ken de manier waarbij je de matrix diagonaliseert, dat kan bij deze matrix niet omdat er geen basis van eigenvectoren is. Er is wel een matrix te maken zodat (als we de matrix met eigenvectoren als kolommen V noemen, de matrix waarvan ik de diagonaalmatrix wil hebben M en de diagonaalmatrix met eigenwaarden L):
MV = VL
Maar nu is v niet inverteerbaar, omdat zijn determinant 0 is.
Ken je de Jordan-normaalvorm van een matrix?
pi_108239927
quote:
0s.gif Op dinsdag 21 februari 2012 20:53 schreef thabit het volgende:

[..]

Ken je de Jordan-normaalvorm van een matrix?
Ik denk dat dat is waar ik naar op zoek ben ja. Het is wel een keer kort behandeld, maar blijkbaar niet blijven hangen. Ik zoek het wel op in mijn dictaat lineaire algebra. Dankje, ouwe baas _O_
pi_108303927
Oke morgen tentamen, ik heb een gedefinieerde integraal

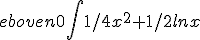
e boven 0 \int 1/4x^2 + 1/2 ln x

wordt: 1/4e^2+ 1/2 - 0 toch?? In het antwoordmodel staat dat als je 0 invult in de formule je er 1/4e uitkrijgt??

Waar staat btw dat wiskundescript? ik kopieer het nu uit vorige post maar zie het niet ergens staan
pi_108304181
\int (\frac{1}{4}x^2 + \frac{1}{2} \ln{x})dx = \frac{1}{12}x^3 + \frac{1}{2}(x\ln{x} - x) +C

waarbij C een constante is. Grenswaarden invullen geeft

\frac{1}{12}x^3 + \frac{1}{2}(x\ln{x} - x)|^e_0 =[ \frac{1}{12}e^3 + \frac{1}{2} (e - e)] - 0 = \frac{1}{12}e^3

Je zou alle tussenstappen moeten opschrijven. Dus eerst de primitieve uitrekenen met de rekenregeltjes die je kent, en dan de grenswaarden invullen. Haakjes gebruiken en de maat dx opschrijven helpt ook.

Het lijkt net alsof jij niet primitiveert, maar gewoon de grenswaarden in de integrand invult.

quote:
In het antwoordmodel staat dat als je 0 invult in de formule je er 1/4e uitkrijgt??
Waar invult? In de bovengrens? Ondergrens? Iets anders?

Mijn ervaring is dat als je je vragen heel precies opschrijft, je vaak al bij de helft van je antwoord bent. En voor de persoon die je probeert te helpen is precisie wel zo fijn :)
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
  donderdag 23 februari 2012 @ 15:28:12 #234
75592 GlowMouse
l'état, c'est moi
pi_108304280
quote:
99s.gif Op dinsdag 21 februari 2012 11:51 schreef Sokz het volgende:
En een constante 'C' ? :P
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
pi_108304640
Oh shit Haushofer, hij was al geintegreerd, ik had er eigenlijk andere dingen omheen moeten zetten dus zo:

Bovengrens: e
Ondergrens: 0

de integraal had ik al berekend, dus [1/4x^2 + 1/2 ln x]

als ik hierin de grenzen invul krijg ik toch1/4e^2 + 1/2 - 0
Volgens het antwoordmodel moet het 1/4e^2+ 1/2 - 1/4 = 1/4e^2 + 1/4
pi_108310610
[\frac{1}{4} e^2 + \frac{1}{2} \ln{e}] - [\frac{1}{4} 0^2 + \frac{1}{2}\ln{0} ] is niet gedefinieerd, aangezien

\lim_{x \rightarrow 0} (\ln{x})

niet bestaat; los uit de pols zou je kunnen zeggen dat



Dus ik vrees dat je ergens een foutje maakt. Wat is volgens jou de logaritme van 0?

Als y = \ln{x}, dan x = e^y . Als x=0, wat gebeurt er dan met y?
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
pi_108331833
Ik volg nu onderbouw vwo (lees: een naar alle waarschijnlijkheid basis der basisvragen) en ik heb een vraag, of nou ja; ik kom er niet uit. Ik heb net een aantal hoofdstukken wiskunde B afgerond en dat ging voornamelijk over breuken. Aftrekken, optellen, delen en vermenigvuldigen. Alles ging goed en alle oefenvragen heb ik goed gemaakt, maar dan komen de huiswerkopgaven en dan worden er sommen gegeven met negatieve getallen (Dit is ook geen 1 keer voor gekomen in de oefenopgaven) :{ En dat snap ik niet.

-13/5 minus 24/6 :X :?

Zou iemand mij dit stapsgewijs willen uitleggen, dan probeer ik het toe te passen op de andere sommen waar ook plotseling met negatieve getallen wordt gewerkt :(
  vrijdag 24 februari 2012 @ 00:50:33 #239
75592 GlowMouse
l'état, c'est moi
pi_108332356
-1\frac{3}{5} - 2\frac{4}{6} = \frac{-8}{5} - \frac{16}{6} = \frac{-48}{30} - \frac{80}{30} = \frac{-128}{30} = \frac{-64}{15} = -4\frac{4}{15}
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
pi_108332482
quote:
0s.gif Op vrijdag 24 februari 2012 00:50 schreef GlowMouse het volgende:
-1\frac{3}{5} - 2\frac{4}{6} = \frac{-8}{5} - \frac{16}{6} = \frac{-48}{30} - \frac{80}{30} = \frac{-128}{30} = \frac{-64}{15} = -4\frac{4}{15}
Mag ik jou vriendelijk bedanken
actieve topics nieuwe topics
abonnement Unibet Coolblue Bitvavo
[Bèta wiskunde] Huiswerk- en vragentopic
Index

» school, studie en onderwijs

Forum Opties
Forumhop:
Hop naar:
(afkorting, bv 'KLB')