SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Baas! Ik moest even denken, maar nu valt alles op zijn plek. Zo simpel... Ik heb me er een beetje op zitten doodstaren! Super bedanktquote:Op dinsdag 6 december 2011 00:11 schreef twaalf het volgende:
Je hebt. Differentieer nu beide kanten naar y.
(ik voel me vaak na een vraag in dit topic erg stom, en dit is geen uitzondering
)
Ja vanaf die kant ben ik er nog niet uit, als je echter vanaf de andere kant werkt:quote:
Over je edit, integreren geeft (1/dx)*(y2/2)
d/dx 0.5y^2 = d/dy dy/dx 0.5y^2 = d(0.5y^2)/dy*dy/dx = y*dy/dx
Beneath the gold, bitter steel
Oh ja, stom. Zo is het wel duidelijk, maar andersom vind ik 't lastig om te zien.quote:
Dat is de kettingregel:
d/dx (y(x))˛ = 2y(x) * y'(x)
Bedankt. Goede tip.quote:
Var(Uniform) = (b-a)^2 / 12 dus Std = sqrt(Var) = b-a/12
TE bepalen zoals hierboven getoond of kijk hier even bij moment-generating functions voor een andere manier.
Ook bedankt, maar aangezien dit tentamen van mij, geloof het of niet, non-calculus is, ga ik er nu even niet op in (ik zit ook even niet in deze stof).quote:
[..]
Als U ~ Uniform(a,b), dan
Nu jij weer.
Ik heb trouwens nog een vraag.
Verderop in het boek wordt namelijk gesteld:
Klopt dit wel?quote:Conclusie: Based on the sample, you can be 90% confident that the true population mean
of the order totals lies on the interval bounded below by $72.41 and above by
$84.09.
Verderop in het boek wordt namelijk gesteld:
Waarschijnlijk lees ik iets niet goed, maar zijn deze beweringen niet met elkaar in tegenspraak?quote:Let a and b represent the lower and upper boundaries of the 90% confidence
interval for the mean of the population. Is it correct to conclude that there is a
90% probability the true population mean lies between a and b? Explain your
answer.
A confidence interval does not describe the probability that any particular
interval constructed around the mean of a single sample will contain the actual
population mean. In this problem, it would be inaccurate to state that there is
a 90% probability the interval bounded below by a and above by b contains the
population mean.
Een 90% CI voor de mean is iets wat als je het 100 keer zou construeren op basis van 100 aselecte steekproeven, hij naar verwachting 90 keer de ware mean bevat.
De tekst in het tweede rondje klopt niet. Ze ronden daar af op 3 decimalen. Kijk je naar het vierde decimaal, zie je dat 1,64 de juiste afronding is op twee decimalen. Bedenk wel dat je door afronden geen echt 90% CI meer hebt.
De tekst in het tweede rondje klopt niet. Ze ronden daar af op 3 decimalen. Kijk je naar het vierde decimaal, zie je dat 1,64 de juiste afronding is op twee decimalen. Bedenk wel dat je door afronden geen echt 90% CI meer hebt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Erg leuk, die tekstballonnetjes. 
Volgens mij bedoelen ze een wel heel subtiel verschil. Er is een kans van 90% dat een gevonden interval de ware E bevat. Er is geen kans van 90% dat het gevonden interval de ware E bevat.
Volgens mij bedoelen ze een wel heel subtiel verschil. Er is een kans van 90% dat een gevonden interval de ware E bevat. Er is geen kans van 90% dat het gevonden interval de ware E bevat.
Bedankt voor jullie reacties.
Based on the sample, you can be 90% confident that the true population mean
of the order totals lies on the interval bounded below by $72.41 and above by
$84.09.
en
Based on the sample, there is a 90% probability that the true population mean
of the order totals lies on the interval bounded below by $72.41 and above by
$84.09.
Het komt bij mij toch hetzelfde over. Als je zegt dat je ergens "zeker" over bent, dan impliceer je daarmee een bepaalde kans. Het kan natuurlijk ook zo zijn dat ik normaal taalgebruik en statisch taalgebruik door elkaar haal.
Textueel gezien merk ik dat nu ook op. Toch knaagt er nog iets. Ik vind het verschil tussen deze twee opties niet helemaal overtuigend nog:quote:
Ik concludeer er zelf uit dat 'confidence' iets anders is dan 'probability'.
Based on the sample, you can be 90% confident that the true population mean
of the order totals lies on the interval bounded below by $72.41 and above by
$84.09.
en
Based on the sample, there is a 90% probability that the true population mean
of the order totals lies on the interval bounded below by $72.41 and above by
$84.09.
Het komt bij mij toch hetzelfde over. Als je zegt dat je ergens "zeker" over bent, dan impliceer je daarmee een bepaalde kans. Het kan natuurlijk ook zo zijn dat ik normaal taalgebruik en statisch taalgebruik door elkaar haal.
Maar als je dan een willekeurige steekproef daarvan neemt, dan is er toch een kans van 90% dat de ware mean daarin zit?quote:
Een 90% CI voor de mean is iets wat als je het 100 keer zou construeren op basis van 100 aselecte steekproeven, hij naar verwachting 90 keer de ware mean bevat.
Op wikipedia staat ook
enquote:A confidence interval does not predict that the true value of the parameter has a particular probability of being in the confidence interval given the data actually obtained.
Maar wat klopt er dan niet aan mijn beredenering?quote:A confidence interval with a particular confidence level is intended to give the assurance that, if the statistical model is correct, then taken over all the data that might have been obtained, the procedure for constructing the interval would deliver a confidence interval that included the true value of the parameter the proportion of the time set by the confidence level.
Om even mijn eigen vraag te beantwoorden. Wat er niet klopt aan mijn beredenering is dat je niet zomaar een willekeurige steekproef hebt, maar je hebt de steekproef waarmee je de CI berekend hebt. Ik denk dat het daar mis gaat.quote:
[..]
Maar wat klopt er dan niet aan mijn beredenering?
Het is allemaal heel subtiel. Ik vergelijk het met een dobbelsteen die je hebt gegooid maar waarvan je de ogen nog niet hebt gezien. Dan kun je niet meer zeggen dat de kans dat de 1 boven ligt 1/6de is.quote:
[..]
Maar als je dan een willekeurige steekproef daarvan neemt, dan is er toch een kans van 90% dat de ware mean daarin zit?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dat het subtiel is is duidelijk, maar ik kan er nog steeds niet helemaal de vinger op leggen waarom het zo is.quote:
[..]
Het is allemaal heel subtiel. Ik vergelijk het met een dobbelsteen die je hebt gegooid maar waarvan je de ogen nog niet hebt gezien. Dan kun je niet meer zeggen dat de kans dat de 1 boven ligt 1/6de is.
Dat van die dobbelsteen snap ik wel. Als je hem gegooid hebt dan heeft ie een bepaalde waarde aangenomen in {1,...,6}. De waarde die hij aan heeft genomen heeft ie dus met kans 1 en de rest met kans 0. Als je gaat kijken (zonder voorkennis) heb je echter wel een kans van 1/6 dat je die 1 aantreft.
Ik zie de analogie met het CI-probleem trouwens niet, behalve dat dit ook subtiel is.
Je kunt zeggen dat ![\mathbb{P}([X_1,X_2]\ni \mu)=1-\alpha](https://forum.fok.nl/lib/mimetex.cgi?%5Cmathbb%7BP%7D%28%5BX_1%2CX_2%5D%5Cni%20%5Cmu%29%3D1-%5Calpha)
. Maar je kunt natuurlijk niet zeggen dat ![\mathbb{P}(\mu \in [x_1,x_2])=1-\alpha](https://forum.fok.nl/lib/mimetex.cgi?%5Cmathbb%7BP%7D%28%5Cmu%20%5Cin%20%5Bx_1%2Cx_2%5D%29%3D1-%5Calpha)
, let op het verschil tussen grote en kleine letters en de afwezigheid van stochasten..
Volgens mij heeft het te maken met een misvatting die heerst. Zo denken mensen dat de kans op kop of munt met een eerlijke munt gelijk is aan respectievelijk 0.5 en 0.5. Toch is de kans slechts bij benadering 0.5 bij een heel groot aantal worpen, bijvoorbeeld 10.000. Zelfs dan zie je dat de proportie niet gelijk is aan 0.5.quote:
[..]
Als je gaat kijken (zonder voorkennis) heb je echter wel een kans van 1/6 dat je die 1 aantreft.
Ik zie de analogie met het CI-probleem trouwens niet, behalve dat dit ook subtiel is.
quote:4.3 Many tosses of a coin. The French naturalist Count Buffon (1707
1788) tossed a coin 4040 times. Result: 2048 heads, or proportion 2048/4040 =
0.5069 for heads.
Around 1900, the English statistician Karl Pearson heroically tossed a coin
24,000 times. Result: 12,012 heads, a proportion of 0.5005.
While imprisoned by the Germans duringWorldWar II, the South African
statistician John Kerrich tossed a coin 10,000 times. Result: 5067 heads, proportion
of heads 0.5067.
quote:Probability describes only what happens in the long
run. Most people expect chance outcomes to show more short-term regularity
than is actually true.
Introduction to the Practice of Statistics, p.238.
Het heeft ermee te maken dat als je het CI eenmaal hebt geconstrueerd, er geen kans meer aan te pas komt om de vraag te beantwoorden of hij de ware parameter bevat. Hij zit erin of hij zit er niet in.quote:
[..]
Ik zie de analogie met het CI-probleem trouwens niet, behalve dat dit ook subtiel is.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dit bevestigt toch gewoon dat er variantie bestaat?quote:
[..]
Volgens mij heeft het te maken met een misvatting die heerst. Zo denken mensen dat de kans op kop of munt met een eerlijke munt gelijk is aan respectievelijk 0.5 en 0.5. Toch is de kans slechts bij benadering 0.5 bij een heel groot aantal worpen, bijvoorbeeld 10.000. Zelfs dan zie je dat de proportie niet gelijk is aan 0.5.
[..]
[..]
Het verhaal van Warren is inderdaad ongerelateerd.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik snap nu de analogie. De parameter zit er inderdaad wel in met kans 1 of niet in met kans 1.quote:
[..]
Het heeft ermee te maken dat als je het CI eenmaal hebt geconstrueerd, er geen kans meer aan te pas komt om de vraag te beantwoorden of hij de ware parameter bevat. Hij zit erin of hij zit er niet in.
Net alsof je een muntje gooit in een afgesloten doos en je niets binnen die doos kan waarnemen. Als je dan het muntje gegooid hebt dan kan je niet meer spreken over 50% kans dat de munt kop is. Maar voor iemand die niet kan waarnemen hoe de munt is gevallen is op dat moment de kans wel 50% dat het kop zal blijken te zijn als je die doos open maakt. Zo is het volgens mij ook voor CI's: zolang je de werkelijke parameter niet kan waarnemen is de kans x % dat die parameter erin zal zitten op het moment dat je die parameter wel zou kunnen waarnemen.
Dus ik zie nog steeds niet waarom:
quote:A confidence interval does not predict that the true value of the parameter has a particular probability of being in the confidence interval given the data actually obtained.
Het percentage mensen dat terwijl ze een vlucht boeken maar niet gaan is 12%. Wat is de propability dat er geen passagier teleurgesteld hoeft te worden als een maatschappij 215 mensen boekt op een vliegtuig van 200?
Dit is de vraag. Nu is mijn vraag, welke formules (verdelingen) moet ik hiervoor gebruiken om het op te lossen?
Dit is de vraag. Nu is mijn vraag, welke formules (verdelingen) moet ik hiervoor gebruiken om het op te lossen?
Je moet aannemen dat de mensen hun beslissing om wel of niet te gaan onafhankelijk van elkaar nemen. Natuurlijk is dat niet zo, bijvoorbeeld als papa en mama niet gaan, gaan de kinderen ook niet. Dan heb je een binomiale situatie (wel of niet gaan) met 215 onafhankelijke trekkingen. We zijn geďnteresseerd in de kans dat er minder dan 15 successen zijn.
Bij zo'n grote trekking en een redelijke kans ga je gewoon normaal benaderen. Laat X het aantal mensen zijn dat niet komt opdagen. X heeft verwachte waarde 215*0.12=25.8 en variantie 215*0.12*0.88=22.7. Dus als n groot is, heeft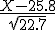
een standaardnormale verdeling.
Nu willen we weten de kans dat X<15. Met een correctie voor continuďteit wordt dit bij een normale benadering X<15.5.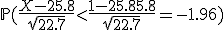
. Normaal gesproken moet je nu de kans opzoeken in een boek, maar -1.96 is een standaardwaarde waarvan de linkerstaart overeenkomt met een kans van 2.5%.
Bij zo'n grote trekking en een redelijke kans ga je gewoon normaal benaderen. Laat X het aantal mensen zijn dat niet komt opdagen. X heeft verwachte waarde 215*0.12=25.8 en variantie 215*0.12*0.88=22.7. Dus als n groot is, heeft
Nu willen we weten de kans dat X<15. Met een correctie voor continuďteit wordt dit bij een normale benadering X<15.5.
