SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Sommatie van conjuctie? Ik neem aan dat je gewoon conjunctie bedoelt van alle elementen in de gegeven verzamelingen.
Volgens mij kan je dat wel zo opschrijven. Je mag vanwege associativiteit de volgorde van conjunctie veranderen, dus de tweede regel kan niet op verschillende manieren geÔnterpreteerd worden.
Volgens mij kan je dat wel zo opschrijven. Je mag vanwege associativiteit de volgorde van conjunctie veranderen, dus de tweede regel kan niet op verschillende manieren geÔnterpreteerd worden.


Ja weet niet hoe je dat noemt als je zeg maar 'sommeerd' over conjunctie maar gewoon conjunctie dus? "Je conjuctie over de elementen van ..." klinkt nogal raar tegenover ... Je sommeert over de elemente van ..."quote:Op zaterdag 26 november 2011 00:03 schreef thenxero het volgende:
Sommatie van conjuctie? Ik neem aan dat je gewoon conjunctie bedoelt van alle elementen in de gegeven verzamelingen.
Volgens mij kan je dat wel zo opschrijven. Je mag vanwege associativiteit de volgorde van conjunctie veranderen, dus de tweede regel kan niet op verschillende manieren geÔnterpreteerd worden.


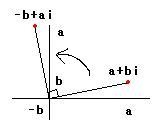
Vraag mbt complexe getallen.
Gegeven:
|1 + i| = Wortel(2)
Arg(1+i) = pi / 4.
Waarom is Arg(1 + i) = pi / 4 ???
Ik kom namelijk uit op Arg 1 + i = 1, want tan arg(1 + i) = b / a = 1 / 1 = 1
Komt het doordat de argument Theta in RADIALEN uitgedrukt wordt?? Dus tan(pi / 4) = 1....klopt dit?
Maar dan zou ik tan-1 arg(w) moeten gebruiken toch?
In het boek staat als theorie:
If w = a + bi, where a = Re(w) != 0, then tan arg(w) = tan arg(a + bi) = b / a. (Dit snap ik allemaal)
Maar ik zit nu even in de knoop met wat tangens precies is, en wanneer je tangens gebruikt, en wanneer je tan-1 (inverse van tangens) gebruikt. Ik weet overigens dat tanx = sinx / cosx.
EDIT
Tan is een verhouding tussen sin en cos. Dus bij complexe getallen, geeft tan(arg(w)) de verhouding weer tussen sin(theta) en cos(theta). Indien deze verhouding 1 is, dan betekent dat de hoek (dus arg(w)) gelijk is aan pi/4.
Klopt dit?
[ Bericht 7% gewijzigd door NonameNogame op 26-11-2011 13:44:57 ]
Gegeven:
|1 + i| = Wortel(2)
Arg(1+i) = pi / 4.
Waarom is Arg(1 + i) = pi / 4 ???
Ik kom namelijk uit op Arg 1 + i = 1, want tan arg(1 + i) = b / a = 1 / 1 = 1
Komt het doordat de argument Theta in RADIALEN uitgedrukt wordt?? Dus tan(pi / 4) = 1....klopt dit?
Maar dan zou ik tan-1 arg(w) moeten gebruiken toch?
In het boek staat als theorie:
If w = a + bi, where a = Re(w) != 0, then tan arg(w) = tan arg(a + bi) = b / a. (Dit snap ik allemaal)
Maar ik zit nu even in de knoop met wat tangens precies is, en wanneer je tangens gebruikt, en wanneer je tan-1 (inverse van tangens) gebruikt. Ik weet overigens dat tanx = sinx / cosx.
EDIT
Tan is een verhouding tussen sin en cos. Dus bij complexe getallen, geeft tan(arg(w)) de verhouding weer tussen sin(theta) en cos(theta). Indien deze verhouding 1 is, dan betekent dat de hoek (dus arg(w)) gelijk is aan pi/4.
Klopt dit?
[ Bericht 7% gewijzigd door NonameNogame op 26-11-2011 13:44:57 ]


Tangens is overstaande zijde gedeeld door aanliggende zijde. Hier: tan(arg(w)) = 1/1, dus arg(w) = tin-1(1)
Kijk ook eens naar http://en.wikipedia.org/w(...)ustration_modarg.svg
Kijk ook eens naar http://en.wikipedia.org/w(...)ustration_modarg.svg
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dat heeft er waarschijnlijk mee te maken dat je dat laatste veel vaker hebt gehoord dan dat eerste.quote:Op zaterdag 26 november 2011 00:59 schreef Dale. het volgende:
[..]
Ja weet niet hoe je dat noemt als je zeg maar 'sommeerd' over conjunctie maar gewoon conjunctie dus? "Je conjuctie over de elementen van ..." klinkt nogal raar tegenover ... Je sommeert over de elemente van ..."


Zou iemand me uitkunnen leggen hoe ik de formule
Bedankt voor jullie hulp alvast.
anders kan schrijven? Is dat dan?quote:K*L-3/2
Of slaat dat nergens op?quote:K / (0.5*(sqrtL))
Bedankt voor jullie hulp alvast.


Je zou 'm zo kunnen schrijven:quote:Op zaterdag 26 november 2011 14:23 schreef Snuf. het volgende:
Zou iemand me uitkunnen leggen hoe ik de formule
[..]
anders kan schrijven? Is dat dan?
[..]
Of slaat dat nergens op?
Bedankt voor jullie hulp alvast.
The biggest argument against democracy is a five minute discussion with the average voter.


Kijk eens even hier en dan vooral dit plaatje. Voor a > 0 geldt Arg(a+bi) = arctan(b/a). Gebruik liever niet de (vooral Amerikaanse) notatie tan-1x voor arctan x.quote:Op zaterdag 26 november 2011 13:39 schreef NonameNogame het volgende:
Vraag mbt complexe getallen.
Gegeven:
|1 + i| = Wortel(2)
Arg(1+i) = pi / 4.
Waarom is Arg(1 + i) = pi / 4 ???
Edit: ik zie net dat je boek beweert dat dit ook zou gelden voor a < 0. Maar dat klopt niet. Om te beginnen is arg(z) voor een complex getal z (ongelijk aan nul) slechts bepaald tot op een geheel veelvoud van 2π. Je kunt dus niet zeggen dat arg(1+i) gelijk is aan ¼π. Wat wťl correct is, is dat arg(1+i) = ¼π + 2kπ, k ∈ Z.
Vooral in angelsaksische literatuur wordt vaak onderscheid gemaakt tussen arg(z) en Arg(z), waarbij met het laatste de zogeheten 'hoofdwaarde' van het argument van z wordt aangegeven. Hiermee wordt doorgaans de unieke waarde van arg(z) op het interval (-π, π] bedoeld. En zo kunnen we dus inderdaad zeggen dat Arg(1+i) = ¼π. Maar omdat arctan(b/a) voor a,b ∈ R (a ≠ 0) alleen waarden op het interval (-½π, ½π) aanneemt, kan Arg(a+bi) dus alleen gelijk zijn aan arctan (b/a) voor a > 0.
[ Bericht 16% gewijzigd door Riparius op 27-11-2011 20:02:38 ]


Als A,B,C onafhankelijk exponentieel verdeeld zijn met parameters 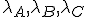 , wat is dan P(A<B<C) ?
, wat is dan P(A<B<C) ?
Ik heb bedacht dat
P(A<B<C) = P(A<B<C | A=min{A,B,C}) P(A=min{A,B,C}) = P(B<C | A=min{A,B,C}) P(A=min{A,B,C}),
maar weet niet hoe ik verder kan.
Ik heb bedacht dat
P(A<B<C) = P(A<B<C | A=min{A,B,C}) P(A=min{A,B,C}) = P(B<C | A=min{A,B,C}) P(A=min{A,B,C}),
maar weet niet hoe ik verder kan.


P(A<B<C) = P({A < max{B,C}} en {B<C}) =P(A<max{B,C})P(B<C)
De verdeling van max{B,C} kun je zo bepalen, en dan zijn die kansen makkelijk uit te rekenen.
De verdeling van max{B,C} kun je zo bepalen, en dan zijn die kansen makkelijk uit te rekenen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


P(max{B,C} < x ) = P(B<x, C<x) = P(B<x) P(C<x)
Dus max{B,C} is Exp(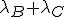 ) verdeeld.
) verdeeld.
edit: Thanks ik ben eruit
[ Bericht 18% gewijzigd door thenxero op 28-11-2011 16:23:12 ]
Dus max{B,C} is Exp(
edit: Thanks ik ben eruit
[ Bericht 18% gewijzigd door thenxero op 28-11-2011 16:23:12 ]


Ja precies. Ik had het ook nog op mijn eigen manier uitgerekend en gebruikt dat {B<C} onafhankelijk is van {A=min{A,B,C}} en daar kwam hetzelfde uit.quote:


Ik probeer te bewijzen dat als:
(domein D in R, en punt c in D, en f:D -> R continu in c)
Als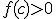 dan bestaat er een
dan bestaat er een 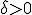 zo dat voor alle
zo dat voor alle 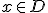 met
met 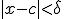 geldt dat
geldt dat 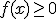 .
.
Ik heb geprobeerd te werken met de definitie van continuiteit en dan f(c) als epsilon maar hiermee liep ik vast. Weet iemand of dit toch goed gaat of misschien een andere manier?
(domein D in R, en punt c in D, en f:D -> R continu in c)
Als
Ik heb geprobeerd te werken met de definitie van continuiteit en dan f(c) als epsilon maar hiermee liep ik vast. Weet iemand of dit toch goed gaat of misschien een andere manier?


Uit continuiteit volgt |f(x) - f(c)| < f(c) met f(c) > 0.
Als f(x) groter gelijk f(c) dan dus ook f(x) > 0.
Als f(x) < f(c) dan moet gelden:
f(c) - f(x) < f(c) dus f(x) > 0.
Dus f(x) groter gelijk 0.
Is dit correct of mis ik iets?
Als f(x) groter gelijk f(c) dan dus ook f(x) > 0.
Als f(x) < f(c) dan moet gelden:
f(c) - f(x) < f(c) dus f(x) > 0.
Dus f(x) groter gelijk 0.
Is dit correct of mis ik iets?


Nee. De continuÔteit van f in c houdt in dat er ook bij ε = f(c) > 0 een δ > 0 bestaat zodanig dat:quote:Op maandag 28 november 2011 22:13 schreef Anoonumos het volgende:
Uit continuiteit volgt |f(x) - f(c)| < f(c) met f(c) > 0.
| f(x) - f(c) | < f(c) voor | x - c | < δ
Bedenk dat | f(x) - f(c) | = f(x) - f(c) voor f(x) ≥ f(c) en | f(x) - f(c) | = f(c) - f(x) voor f(x) ≤ f(c).quote:Als f(x) groter gelijk f(c) dan dus ook f(x) > 0.
Als f(x) < f(c) dan moet gelden:
f(c) - f(x) < f(c) dus f(x) > 0.


Riparius, Hartelijk dank voor je uitleg en links! Ik heb echter nog een aantal vraagjes, om te controleren of ik het helemaal snap:quote:
Ik moest Arg(z) berekenen, de modules bepalen, en z in r (= |z|) en theta herschrijven
Vraag 10)
Gegeven: z = -2 + i
Mijn uitwerking:
a = -2, b = 1
dus r = |z| = Wortel(a^2 + b^2) = Wortel(4 + 1) = Wortel(5);
En Arg(z) -----> arctan(1/-2). Antwoord gaf aan: Arg(z) = π - arctan(1/2).
Is dit omdat a < 0 en b >= 0, en er dus geldt: Arg(z) = arctan(b/a) + π ?? Zo ja, dan wordt het antwoord dat ik hiermee verkrijg Arg(z) < -π -----> en aangezien de principal argument bereik (-π, π] heeft, diende ik π hierbij op te tellen, en dus Arg(z) = π - arctan(1/2) te moeten doen? (zodat het uiteindelijke antwoord tussen het bereik (-π, π] komt te liggen, wat voldoet aan het bereik van de principal Argument)
Een 2e vraag met deze opgave: Uit het gegeven, blijkt dat a = -2. Waarom geeft het antwoord dan arctan(1 / 2) aan? (ipv arctan(1 / -2)).
Vraag 11)
Gegeven: z = -3 - 4i
Mijn uitwerking:
a = -3, b = -4
dus r = |z| = Wortel(a^2 + b^2) = Wortel(9+16) = 5
En Arg(z) -----> arctan(-4 / -3). Aangezien zowel a<0 en b<0, moet ik dus doen: Arg(z) = arctan(-4 / -3) - π
Maar arctan(-4 / -3) = 0.9272... -> Dit valt toch binnen de range (-π, π], en dus voldoet aan de range voor de principal Argument???
Het antwoord voor Arg(z) was overigens: Arg(z) = arctan(4/3) + π (waarom positieve a- en b-waarden en wordt er π BIJgeteld??? Zou je &pi niet AF moeten trekken? immers, a en b zijn beide kleiner dan 0, en in dat geval moet je &pi aftrekken, zoals aangegeven was op de wikipedia pagina)
Vraag 12)
Gegeven: z = 3 - 4i
Mijn uitwerking:
a = 3, b = -4
r = |z| = 5
En Arg(z) = arctan(-4 / 3) -----> omdat a > 0 , hoef ik hier geen π bij op te tellen.
Antwoord was: Arg(z) = - arctan(4 / 3) ......... Waarom b = positief nu? Kan dit?
Voor vraag 12, waarom b positief is en -arctan(b / a) geschreven wordt ipv arctan(-b / a), kan ik wel wat afleiden aan de hand van goniometrie en de eenheidscirkel (simpelweg zoals in vwo-stof wiskunde staat), namelijk:
sin(-x) = -sin(x).....Zoals in de afbeelding aangegeven:
Mijn vraag hierbij is....klopt mijn redenatie? Zo ja, dan snap ik waarom arctan(-4 / 3) herschreven kan worden in -arctan(4 / 3)
Vraag 12, deel 2)
De herschrijving van z in r (= |z|) en theta
Gegeven was: z = 3 -4i
Mijn uitwerking:
a = 3
b = -4
r = |z| = 5
Er geldt verder: sinθ = b / r ..... en ..... cosθ = a / r, dan b = r∑sinθ en a = r∑cosθ
Aangezien de algemene regel geldt: z = a + bi (in dit geval is b negatief), dus z = a + -bi, geldt:
z = r∑cosθ + i∑r∑sinθ ---------> z = 5(cosθ - i∑sinθ) (want b was negatief)
Antwoord luidt: z = 5(cosθ + i∑sinθ)........... waarom??
Een vraag hierbij is o.a.: Hoe moet ik z = 3 - 4i nu zien, als z = a + bi (met b is negatief), of als z = a - bi (met b is positief) ??
------------------------------------
Mijn excuses voor de vele en lange vragen. Ik heb geen leraar 'bij de hand' en tevens is wiskunde niet mijn studie of een onderdeel ervan. Ik vind het echter behoorlijke leuk en interessant en ik doe aan zelfstudie. Nadeel is dat ik alles zelf uit moet zoeken zonder leraar. Vandaar het gebruik van dit forum.
Alvast enorm bedankt!!
[ Bericht 0% gewijzigd door NonameNogame op 29-11-2011 22:48:13 ]


Over het algemeen helpt het om aan poolcoŲrdinaten te denken. Heb je een complex getal:quote:Op dinsdag 29 november 2011 22:42 schreef NonameNogame het volgende:
[..]
Riparius, Hartelijk dank voor je uitleg en links! Ik heb echter nog een aantal vraagjes, om te controleren of ik het helemaal snap:
Ik moest Arg(z) berekenen, de modules bepalen, en z in r (= |z|) en theta herschrijven
Vraag 10)
Gegeven: z = -2 + i
Mijn uitwerking:
a = -2, b = 1
dus r = |z| = Wortel(a^2 + b^2) = Wortel(4 + 1) = Wortel(5);
En Arg(z) -----> arctan(1/-2). Antwoord gaf aan: Arg(z) = π - arctan(1/2).
(1) z = x + yi,
dan is het beeldpunt van dit getal in het complexe vlak het punt met coŲrdinaten (x;y). Maar nu kun je de cartesische (rechthoekige) coŲrdinaten van een punt ook omzetten naar poolcoŲrdinaten. Heb je een punt P(x;y) dan moet je naar twee dingen kijken voor deze omzetting, namelijk de afstand OP = r (met de r van radius 'straal'), en de hoek die OP maakt met de positieve x-as. Stel dat we de positieve x-as over een hoek θ (uitgedrukt in radialen) moeten roteren om de (halve) lijn vanuit de oorsprong door punt P te krijgen, dan geldt voor de coŲrdinaten van punt P(x;y):
(2) x = r∙cos θ
(3) y = r∙sin θ
En daar P(x;y) het beeldpunt is van ons complexe getal z = x + yi hebben we dus:
(4) z = r∙cosθ + i∙r∙sin θ = r(cos θ + i∙sin θ)
De poolcoŲrdinaten van het beeldpunt P van z zijn dus (r;θ). Merk op dat we hier gewoonlijk i∙sin θ schrijven omdat sin θ∙i gemakkelijk aanleiding zou kunnen geven tot verwarring. Je kunt eenvoudig nagaan waarom (2) en (3) en dus ook (4) gelden, als je nog even terugdenkt aan de definitie van de sinus- en cosinusfunctie aan de hand van de eenheidscirkel. Noem je het snijpunt van lijnstuk OP of het verlengde daarvan met de eenheidscirkel P', dan zijn de coŲrdinaten van dit punt P' per definitie (cos θ ; sin θ) omdat de cosinus en de sinus van θ gedefinieerd zijn als de x- resp. de y-coŲrdinaat van het beeldpunt van (1;0) bij rotatie om de oorsprong over een hoek θ. En aangezien punt P het beeldpunt is van punt P' bij een meetkundige vermenigvuldiging ten opzichte van O met een factor r is het direct duidelijk dat de coŲrdinaten van punt P dus inderdaad (r∙cos θ ; r∙sin θ) zijn.
Nu noemen we de afstand tot de oorsprong van het beeldpunt P(x;y) van het complexe getal z = x + yi de modulus (of: absolute waarde) van z, en geven we deze aan met abs(z) of |z|. Op grond van de stelling van Pythagoras is meteen duidelijk dat we hebben:
(5) |z| = √(x2 + y2)
De rotatiehoek θ heet het argument van z, en deze wordt aangegeven met arg(z). Maar nu is het zo dat we na een (extra) rotatie om de oorsprong over 2π radialen, hetzij met de wijzers van de klok mee (negatief) hetzij tegen de wijzers van de klok in (positief), weer op precies hetzelfde punt uitkomen. Daarom is arg(z) niet eenduidig bepaald, maar slechts tot op een geheel veelvoud van 2π.
Nu is het in de praktijk vaak nuttig om toch over 'het' argument van een complex getal te kunnen spreken, daarom heeft men bedacht dat je de rotatie van de positieve x-as (reŽle as) kunt beperken tot een halve slag linksom (positief, tegen de wijzers van de klok in),of een halve slag rechtsom (negatief, met de wijzers van de klok mee). Zo kunnen we het argument altijd uitdrukken als een hoek die ligt tussen -π en +π radialen.
Alleen: wat moeten we dan doen met punten op de negatieve reŽle as? Want voor de getallen waarvan het beeldpunt op de negatieve reŽle as ligt zou je dan nog steeds net zo goed kunnen zeggen dat het argument -π is als π. De conventie is dat we dan voor de getallen op de negatieve reŽle as de positieve waarde π nemen. Alles samengevat ligt de 'hoofdwaarde' van het argument dan altijd op het interval (-π,π]. Deze 'hoofdwaarde' van het argument van z wordt vooral in Amerikaanse boeken aangeduid als Arg(z), dus met een hoofdletter.
Je kunt de negatieve reŽle as nu een beetje vergelijken met de datumgrens op aarde: als je naar het westen reist, dan kom je gaandeweg in tijdzones waar het steeds een uur vroeger is, en als je naar het oosten reist dan kom je gaandeweg in tijdzones waar het steeds een uur later is. Maar omdat de aarde rond is, kom je dan als je naar het oosten reist uiteindelijk op een punt waar je ineens overgaat van GMT+12 uur naar GMT-12 uur. Je maakt dan een sprong van precies ťťn dag terug in de tijd en als je dan verder blijft reizen in oostelijke richting blijf je steeds in tijdzones terecht komen waar het een uur later is. Zoiets hebben we nu ook met de 'hoofdwaarde' van het augment in het complexe vlak. Als we starten in het punt (1;0), dus het beeldpunt van het (reŽle) getal 1, en we roteren dit punt tegen de klok in, dan neemt het argument toe tot π en we op de negatieve reŽle as zitten. Maar zodra we verder roteren en de negatieve reŽle as zijn gepasseerd hebben we een sprong gemaakt waarbij het argument met 2π is verminderd. Draaien we dan verder tegen de wijzers van de klok in, dan blijft het argument toenemen vanaf -π tot we weer op het uitgangspunt (1;0) terug zijn, en dan is het (hoofd)argument weer 0.
Nu dan je vraag. Je wil Arg(-2 + i) berekenen, dus de 'hoofdwaarde' van het argument van -2 + i. Het eerste wat je dan altijd even moet doen (in gedachten) is de ligging van het beeldpunt van dit getal in het complexe vlak visualiseren. In dit geval gaat het om het punt met de coŲrdinaten (-2;1), en dat punt ligt in het tweede kwadrant (meestal worden de kwadranten aangegeven met Romeinse cijfers, dus kwadrant II). Dan zie je meteen dat (a) Arg(-2 + i) positief moet zijn, want (-2;1) ligt in de bovenste helft van het vlak en (b) dat de waarde in ieder geval moet liggen tussen ½π en π. Pas als je dit bedacht hebt moet je gaan rekenen.
Laten we het punt (-2;1) waar het hier om gaat weer even P noemen. Maak je nu een schetsje, dan zie je dat lijnstuk OP een hoek θ maakt met de negatieve reŽle as (x-as) zodanig dat
(6) tan θ = 1 : 2 = ½
en dus is:
(7) θ = arctan(½)
Maar ja, we moeten niet de hoek van lijnstuk OP met de negatieve reŽle as hebben, maar de hoek met de positieve reŽle as, en die hoek is supplementair met hoek θ. Twee hoeken noemen we supplementair als ze samen een gestrekte hoek vormen, dus een hoek van 180 graden oftewel π radialen. Voor de gezochte hoek, en daarmee voor het 'hoofdargument' van het complexe getal -2 + i vinden we dus:
(8) Arg(-2 + i) = π - arctan(½)
Maar goed, waarom werkt het niet als we gewoon arctan(1/-2) nemen zoals jij deed? Nu, dat heeft te maken met het bereik van de arctan functie. De arctan functie is de inverse functie van de tangens functie, en die geeft de hoek aan (in radialen) waarvan de tangens gelijk is aan de gegeven waarde (hier -½). De aanduiding arctan is een afkorting van arcus tangens (met arcus 'boog' omdat een hoekmaat in radialen ook als een cirkelboog op de eenheidscirkel is op te vatten). Maar nu is de tangens evenals de sinus en de cosinus een periodieke functie en wel een periodieke functie met een periode π (dit in tegenstelling tot de sinus en cosinus die elk een periode 2π hebben). Omdat de tangens een periodieke functie is kunnen we dus ook niet spreken over 'de' hoek (of: rotatie) waarvan de tangens bijvoorbeeld -½ is, want er zijn oneindig veel hoeken (rotaties) waarbij de tangens -½ is, en deze hoeken (rotaties) verschillen allemaal een geheel veelvoud van π met elkaar. En dus moest men een keuze maken.
Nu is het zo dat de tangens van een hoek θ precies ťťnmaal alle waarden op R aanneemt als we θ het open interval (-½π, ½π) laten doorlopen, en dus kunnen we dit ook omkeren en zo bij elke x uit R precies ťťn waarde θ op het interval (-½π, ½π) aanwijzen waarvoor geldt dat tan θ = x. We zeggen dan dat arctan x = θ. Met arctan x wordt dus bedoeld de hoek (in radialen) op het interval (-½π, ½π) waarvan de tangens gelijk is aan x. Zo is trouwens ook de notatie te verklaren: vroeger schreef men arc. tan. x (met puntjes, als afkorting) en bedoelde men hiermee 'de boog (arcus) waarvan de tangens x is'.
Maar goed, de arctan functie neemt dus op R alleen waarden aan op het interval (-½π, ½π) en dat verklaart waarom Arg(a + bi) niet gelijk kan zijn aan arctan(b/a) voor a < 0.
Zo kun je het beredeneren, maar het is om vergissingen te voorkomen beter om het altijd eerst even te visualiseren.quote:Is dit omdat a < 0 en b >= 0, en er dus geldt: Arg(z) = arctan(b/a) + π ?? Zo ja, dan wordt het antwoord dat ik hiermee verkrijg Arg(z) < -π -----> en aangezien de principal argument bereik (-π, π] heeft, diende ik π hierbij op te tellen, en dus Arg(z) = π - arctan(1/2) te moeten doen? (zodat het uiteindelijke antwoord tussen het bereik (-π, π] komt te liggen, wat voldoet aan het bereik van de principal Argument)
Dat is hopelijk duidelijk uit het bovenstaande. Ze zijn (impliciet) uitgegaan van de supplementaire hoek. Je zou het antwoord ook kunnen schrijven als π + arctan(1/-2) aangezien arctan(-x) = -arctan(x).quote:Een 2e vraag met deze opgave: Uit het gegeven, blijkt dat a = -2. Waarom geeft het antwoord dan arctan(1 / 2) aan? (ipv arctan(1 / -2)).
Grote verwarring. Zowel je eigen antwoord als het antwoord dat het boek geeft (als je dat juist hebt overgenomen) zijn niet correct. Wikipedia doet het wel goed. Het beeldpunt (-3;-4) van -3 - 4i ligt in kwadrant III, dus we kunnen meteen zeggen dat de hoofdwaarde van het argument moet liggen tussen -π en -½π, en dat zie ik niet in je antwoorden.quote:Vraag 11)
Gegeven: z = -3 - 4i
Mijn uitwerking:
a = -3, b = -4
dus r = |z| = Wortel(a^2 + b^2) = Wortel(9+16) = 5
En Arg(z) -----> arctan(-4 / -3). Aangezien zowel a<0 en b<0, moet ik dus doen: Arg(z) = arctan(-4 / -3) - π
Maar arctan(-4 / -3) = 0.9272... -> Dit valt toch binnen de range (-π, π], en dus voldoet aan de range voor de principal Argument???
Het antwoord voor Arg(z) was overigens: Arg(z) = arctan(4/3) + π (waarom positieve a- en b-waarden en wordt er π BIJgeteld??? Zou je &pi niet AF moeten trekken? immers, a en b zijn beide kleiner dan 0, en in dat geval moet je &pi aftrekken, zoals aangegeven was op de wikipedia pagina)
Dit antwoord is wel juist. Je maakt hier gebruik van arctan (-x) = -arctan x.quote:Vraag 12)
Gegeven: z = 3 - 4i
Mijn uitwerking:
a = 3, b = -4
r = |z| = 5
En Arg(z) = arctan(-4 / 3) -----> omdat a > 0 , hoef ik hier geen π bij op te tellen.
Antwoord was: Arg(z) = - arctan(4 / 3) ......... Waarom b = positief nu? Kan dit?
Je moet uitgaan van de tangensfunctie. Neem aan dat -½π < θ < ½π en stel tan θ = x. Dan is dus per definitie arctan x = θ. Maar omdat tan(-θ) = -tan θ en tan θ = x is dus tan(-θ) = -x en dus weer per definitie arctan(-x) = -θ. En dus geldt inderdaad arctan(-x) = -arctan x.quote:Voor vraag 12, waarom b positief is en -arctan(b / a) geschreven wordt ipv arctan(-b / a), kan ik wel wat afleiden aan de hand van goniometrie en de eenheidscirkel (simpelweg zoals in vwo-stof wiskunde staat), namelijk:
sin(-x) = -sin(x).....Zoals in de afbeelding aangegeven:
[ afbeelding ]
Mijn vraag hierbij is....klopt mijn redenatie? Zo ja, dan snap ik waarom arctan(-4 / 3) herschreven kan worden in -arctan(4 / 3)
Je introduceert hier zelf een minteken omdat je kennelijk uit wil gaan van een positieve hoek. Maar dat moet je (hier) niet doen, je kunt beter denken in termen van rotaties die zowel positief als negatief kunnen zijn. En dan heb je uitgaande van de positieve reŽle as aan een rotatie over een negatieve hoek tussen 0 en -½π voldoende om uit te komen op een punt in het vierde kwadrant. Formule (4) geldt altijd, ook voor negatieve rotaties, omdat immers de sinus en cosinusfuncties ook zo zijn gedefinieerd aan de hand van de eenheidscirkel.quote:Vraag 12, deel 2)
De herschrijving van z in r (= |z|) en theta
Gegeven was: z = 3 -4i
Mijn uitwerking:
a = 3
b = -4
r = |z| = 5
Er geldt verder: sinθ = b / r ..... en ..... cosθ = a / r, dan b = r∑sinθ en a = r∑cosθ
Aangezien de algemene regel geldt: z = a + bi (in dit geval is b negatief), dus z = a + -bi, geldt:
z = r∑cosθ + i∑r∑sinθ ---------> z = 5(cosθ - i∑sinθ) (want b was negatief)
Antwoord luidt: z = 5(cosθ + i∑sinθ)........... waarom??
Dat is inderdaad de kern. Vroeger, in de 16e en ook in de 17e eeuw, toen men pas leerde 'rekenen met letters' had men grote moeite met het idee om een uitdrukking van de gedaante z = 3 - 4i te 'zien' als z = a + bi met a = 3 en b = -4, en nam men vaak aan dat de letters positieve grootheden voorstelden. En dus 'zag' men z = 3 - 4i als z = a - bi met a = 3 en b = 4. Dat kan, maar je moet het (hier) toch niet doen omdat je dan heel gauw in verwarring raakt met bijvoorbeeld het uitrekenen van het hoofdargument. We hebben hier Arg(3 - 4i) = arctan(-4/3) = -arctan(4/3).quote:Een vraag hierbij is o.a.: Hoe moet ik z = 3 - 4i nu zien, als z = a + bi (met b is negatief), of als z = a - bi (met b is positief) ??
Voor het uitrekenen van het hoofdargument van z = x + yi bestaat een formule die ook werkt als het beeldpunt op de imaginaire as of in de linkerhelft van het complexe vlak ligt (dus voor x ≤ 0), maar om dat te begrijpen moet je wel iets weten van goniometrie.
We hebben gezien dat arctan alleen waarden aanneemt op het interval (-½π, ½π) maar dat het 'hoofdargument' ligt op het interval (-π, π], en dat is nu precies het probleem. Als we nu de (mogelijke) waarde π voor het 'hoofdargument' (getallen op de negatieve reŽle as) even buiten beschouwing laten, dan is het interval (-π, π) dus precies tweemaal zo breed als het interval (-½π, ½π) waarin arctan ligt, en daar kunnen we wat mee doen. Laten we zeggen dat de gezochte hoofdwaarde Arg(z) van z = x + yi (y ≠ 0 voor x ≤ 0) gelijk is aan θ. Dan is dus -π < θ < π, en dus -½π < ½θ < ½π. Maar dit betekent dat:
(9) ½θ = arctan(tan ½θ) (-π < θ < π)
en dus:
(10) Arg(x + yi) = θ = 2∙arctan(tan ½θ) (-π < θ < π)
Als we nu tan ½θ uit kunnen drukken in cos θ = x/r en sin θ = y/r, dan hebben we dus Arg(x + yi) = θ. Hiervoor gaan we uit van de bekende formules voor de sinus en cosinus van de dubbele hoek:
(11a) sin 2α = 2∙sinα∙cos α
(11b) cos 2α = 2∙cos2α - 1
Uit (11b) krijgen we
(11c) 1 + cos 2α = 2∙cos2α
Deling van de leden van (11a) door de leden van (11c) geeft dan:
(11d) sin 2α /(1 + cos 2α) = tan α,
en door substitutie van α = ½θ en dus 2α = θ krijgen we dan:
(12) tan ½θ = sin θ /(1 + cos θ)
Substitutie van (12) in (10) geeft nu:
(13) Arg(x+ yi) = 2∙arctan(sin θ /(1 + cos θ))
en aangezien cos θ = x/r en sin θ = y/r levert substitutie hiervan in (13) na wat vereenvoudiging (vermenigvuldiging van de teller en noemer van het quotiŽnt met r):
(14) Arg(x + yi) = 2∙arctan(y/(r + x)) (y ≠ 0 voor x ≤ 0, r = √(x2 + y2))
Met deze formule kan ik bijvoorbeeld direct zeggen dat het 'hoofdargument' van -3 - 4i gelijk is aan 2∙arctan(-2), hetgeen overigens weer gelijk is aan arctan(4/3) - π zoals je gemakkelijk kunt controleren.
Er zijn nog andere manieren om (de hoofdwaarde van) het argument uit te rekenen die vooral toepasbaar zijn als je over een geschikt programma beschikt of bijvoorbeeld van WolframAlpha gebruik kunt maken. Je weet (hopelijk) dat bij vermenigvuldiging van twee complexe getallen de modulus van het product gelijk is aan het product van de moduli van de factoren en dat het argument gelijk is aan de som van de argumenten van de factoren modulo 2π. Vermenigvuldiging van een complex getal met cos θ + i∙sin θ is meetkundig te interpreteren als een rotatie van het beeldpunt van dat complexe getal om de oorsprong over een hoek θ. Je kunt dit vrij gemakkelijk inzien als je eerst beredeneert dat vermenigvuldiging van een complex getal met i meetkundig is te interpreteren als een rotatie over een rechte hoek oftewel ½π radialen in positieve zin (i.e. tegen de klok in). We hebben i(a + bi) = ai + bi2 = -b + ai. Als je nu de ligging van het beeldpunt (-b;a) van -b + ai ten opzichte van het originele beeldpunt (a;b) van a + bi bekijkt dan zie gemakkelijk (congruente driehoeken) dat vermenigvuldiging met i inderdaad een rotatie in positieve zin over een rechte hoek oftewel ½π rad representeert:
Heb je dit eenmaal gezien, dan is het niet moeilijk om te begrijpen (maak een tekening!) wat er gebeurt als je een complex getal a + bi vermenigvuldigt met cos θ + i∙sinθ. We kunnen het product opsplitsen in twee delen:
(15) (cos θ + i∙sinθ)(a + bi) = cos θ∙(a + bi) + (i∙sinθ)∙(a + bi) = cos θ∙(a + bi) + i∙(sinθ∙(a + bi))
De vermenigvuldiging van een complex getal a + bi met een reŽel getal zoals (hier) cos θ of sin θ is niet zo spannend: dit komt overeen met een meetkundige vermenigvuldiging van het beeldpunt met die reŽle factor (of, zo je wil, de vermenigvuldiging van een vector met een scalar). Het beeldpunt van de vermenigvuldiging van een complex getal a + bi met een reŽel getal ligt dus op dezelfde lijn door de oorsprong als het beeldpunt (a;b) van a + bi. Maar nu hebben we voor het product van a + bi met cos θ + i∙sinθ in het rechterlid van (15) twee componenten, waarvan de tweede component sinθ∙(a + bi) ook nog eens wordt vermenigvuldigd met i. En we hebben net gezien dat vermenigvuldiging met i meetkundig een rotatie tegen de klok in over een rechte hoek representeert. Als we nu lijnstukken tekenen vanuit de oorsprong naar de beeldpunten van elk van de beide complexe getallen cos θ∙(a + bi) en i∙(sinθ∙(a + bi)) in het rechterlid van (15) dan staan die lijnstukken dus loodrecht op elkaar. En dat betekent dat we de afstand van het beeldpunt van de som en daarmee de afstand (de modulus) van het gehele product in (15) eenvoudig kunnen berekenen met de stelling van Pythagoras. Aangezien cos2θ + sin2θ = 1 vinden we voor die afstand dan √(a2 + b2) zodat het beeldpunt van het product dus op dezelfde afstand van de oorsprong ligt als het beeldpunt (a;b) van a + bi zelf. Aan de modulus verandert dus niets door de vermenigvuldiging met cos θ + i∙sin θ zodat het beeldpunt van het product alleen is geroteerd ten opzichte van het beeldpunt (a;b) van a + bi. En aangezien het beeldpunt van de component cos θ∙(a + bi) langs dezelfde lijn ligt als het lijnstuk van de oorsprong naar het punt (a;b) en het beeldpunt van de component i∙(sinθ∙(a + bi)) = sinθ∙(-b + ai) op de lijn door de oorsprong loodrecht daarop, is direct in te zien dat vermenigvuldiging van een complex getal a + bi met cos θ + i∙sin θ correspondeert met een rotatie om de oorsprong van het beeldpunt (a;b) over een hoek θ.
Als je dit eenmaal inziet (en dit is fundamenteel) dan kun je hier aardige dingen mee doen. Als we het getal 1 = 1 + 0i vermenigvuldigen met cos α + i∙sin α dan is de uitkomst uiteraard cos α + i∙sin α en kunnen we zeggen dat het beeldpunt (1;0) van het getal 1 door deze vermenigvuldiging wordt geroteerd over een hoek α zodat het beeldpunt van het product uiteraard (cos α ; sin α) is. Dat is niet zo interessant, maar als we het getal cos α + i∙sin α nu weer met cos β + i∙sin β vermenigvuldigen, dan wordt het beeldpunt (cos α ; sin α) nog eens geroteerd over een hoek β. Maar dan is het beeldpunt (1;0) van het getal 1 dus uiteindelijk geroteerd over een hoek α + β, zodat we kunnen zeggen dat vermenigvuldiging met (cos α + i∙sin α)(cos β + i∙sin β) precies hetzelfde bewerkstelligt als een vermenigvuldiging met cos(α+β) + i∙sin(α+β). Zo komen we tot de conclusie dat geldt:
(16) cos(α+β) + i∙sin(α+β) = (cos α + i∙sin α)(cos β + i∙sin β)
Als je nu de haakjes in het rechterlid van (16) uitwerkt en de rekenregel i2 = -1 gebruikt, dan kun je dit schrijven als:
(17) cos(α+β) + i∙sin(α+β) = (cos α∙cos β - sin α∙sin β) + i∙(sin α∙cosβ + cos α∙sin β)
Maar nu zijn twee complexe getallen uitsluitend aan elkaar gelijk als zowel de reŽle delen als de imaginaire delen aan elkaar gelijk zijn, en dus volgt uit (17) dat:
(18a) cos(α+β) = cos α∙cos β - sin α∙sin β
(18b) sin(α+β) = sin α∙cosβ + cos α∙sin β
Dit zijn de bekende additietheorema's uit de elementaire goniometrie. Er bestaat dus een nauw verband tussen deze somformules en de vermenigvuldiging van complexe getallen.
Aangezien voor een natuurlijk getal n het verheffen tot de macht n van een getal neerkomt op een n maal herhaalde vermenigvuldiging, kun je op grond van (16) ook nog concluderen dat geldt:
(19) (cos θ + i∙sin θ)n = cos nθ + i∙sin nθ
Dit resultaat staat bekend als de formule van De Moivre. Je kunt deze formule bijvoorbeeld gebruiken om eenvoudig goniometrische identiteiten af te leiden voor de sinus en cosinus van een veelvoud van een hoek. Ook kun je deze formule gebruiken om alle oplossingen te vinden van de vergelijking zn = 1. Probeer dat eens uit voor bijvoorbeeld n = 5 en n = 6. Wat kun je zeggen over de beeldpunten van de complexe getallen die de oplossingen vormen van deze vergelijking?
De betrekking arg(z1z2) = arg(z1) + arg(z2) (mod 2π) die tot uitdrukking brengt dat bij vermenigvuldiging van twee complexe getallen de argumenten bij elkaar worden opgeteld (modulo 2π) doet je wellicht denken aan een soortgelijke betrekking bij logaritmen. De logaritme van het product van twee (positieve, reŽle) getallen is gelijk aan de som van de logaritmen van de factoren: log(ab) = log(a) + log(b). Nu zou je kunnen beginnen te vermoeden dat er wellicht een verband bestaat tussen logaritmen en het argument van complexe getallen. Welnu, dat is inderdaad het geval.
Het zou veel te ver voeren om hier een verantwoorde behandeling te geven van logaritmen van complexe getallen, maar ik zal toch proberen het verband tussen complexe logaritmen en het argument op een enigszins intuÔtieve manier duidelijk te maken. Laten we eens aannemen dat het mogelijk is een zinnige betekenis toe te kennen aan een logaritme van een complex getal, waarbij ik even in het midden laat wat we ons daarbij zouden moeten voorstellen. Op grond van (16) hebben we dan:
(20) log(cos(α+β) + i∙sin(α+β)) = log((cos α + i∙sin α)(cos β + i∙sin β))
En omdat we mogen verwachten dat de logaritme van een product gelijk is aan de som van de logaritmen van de factoren zou dan ook moeten gelden:
(21) log(cos(α+β) + i∙sin(α+β)) = log(cos α + i∙sin α) + log(cos β + i∙sin β)
Nu kun je uit (21) opmaken dat de logaritme van een complex getal van de vorm cos θ + i∙sin θ kennelijk recht evenredig zou moeten zijn met θ, en dat is ook in overeenstemming met log(cos 0 + i∙sin 0) = log(1) = 0 voor θ = 0. Maar dan zou log(cos θ + i∙sin θ) dus gelijk moeten zijn aan θ maal een constante, en rijst onmiddellijk de vraag wat die constante dan is.
Laten we zeggen dat:
(22) z = cos θ + i∙sin θ en w = log(z),
zodat:
(23) w = log(cos θ + i∙sin θ)
Nu zou dus moeten gelden dat w recht evenredig is met θ, zodat er een constante c zou moeten zijn zodanig dat:
(24) w = c∙θ
Maar hoe vinden we die geheimzinnige constante c? Wel, als w = c∙θ dan moet gelden dw/dθ = c, zodat we de constante c zouden moeten kunnen vinden door de afgeleide dw/dθ te bepalen. En volgens de kettingregel hebben we dan:
(25) dw/dθ = dw/dz ∙ dz/dθ
Nu zouden we op grond van de afgeleide x-1 van de reŽle functie log(x) kunnen veronderstellen (en meer is dat niet op dit moment) dat voor w = log(z) evenzo moet gelden:
(26) dw/dz = z-1.
De bepaling van dz/dθ levert niet veel moeilijkheden op. De afgeleide van cos θ naar θ is -sin θ en de afgeleide van sin θ naar θ is cos θ. Maar nu is het je wellicht wel eens opgevallen dat je hebt:
(27a) d(cos t)/dt = cos(t + ½π) = -sin t
(27b) d(sin t)/dt = sin(t + ½π) = cos t
De verklaring hiervan is heel eenvoudig als je het even 'fysisch' bekijkt. Heb je een punt dat met een eenparige snelheid van 1 eenheid per seconde tegen de wijzers van de klok in langs de eenheidscirkel beweegt, te beginnen in het punt (1;0) op tijdstip t = 0, dan kun je de plaatsvector van dit punt schrijven als s(t) = cos(t)∙ex + sin(t)∙ey. De afgeleide s'(t) = v(t) = d(cos(t))/dt∙ex + d(sin(t))/dt∙ey is dan de snelheidsvector. Maar: we weten dat dit een vector moet zijn met lengte 1 die op ieder moment loodrecht staat op de plaatsvector, omdat de raaklijn aan een cirkel loodrecht staat op de straal naar het raakpunt. En omdat de beweging tegen de klok in gaat is v(t) een kwart slag in positieve zin gedraaid ten opzichte van s(t) en moet dus ook gelden v(t) = cos(t + ½π)∙ex + sin(t + ½π)∙ey, waaruit direct (27a) en (27b) volgen. Goed, zo hebben we dus:
(28) dz/dθ = cos(θ + ½π) + i∙sin(θ + ½π)
Maar nu weten we ook dat een rotatie over een hoek ½π beantwoordt aan een vermenigvuldiging met i, en dus kunnen we voor (28) schrijven:
(29) dz/dθ = i∙(cos θ + i∙sin θ) = i∙z
Uit (25), (26) en (29) volgt nu dat:
(30) dw/dθ = dw/dz ∙ dz/dθ = z-1 ∙ i∙z = i
We zien nu dat dw/dθ inderdaad een constante is, en deze evenredigheidsconstante c = dw/dθ is niets anders dan de imaginaire eenheid i. En dus volgt uit (23) en (24) dat kennelijk zou moeten gelden:
(31) log(cos θ + i∙sin θ) = i∙θ
Deze betrekking staat bekend als de formule van Cotes (1682-1716), die deze betrekking in 1714 als eerste publiceerde (zij het dat hij dit op een heel andere wijze had gevonden). Nu is er echter een probleem met (31) dat ook Cotes zich destijds niet heeft gerealiseerd. Als we in (31) θ vervangen door θ + 2kπ (k ∈ Ζ), dan krijgen we uiteraard:
(32) log(cos(θ + 2kπ) + i∙sin(θ + 2kπ)) = i∙(θ + 2kπ)
Maar nu zijn de sinus en cosinus periodieke functies met een periode 2π. En dus is cos(θ + 2kπ) = cos θ en sin(θ + 2kπ) = sin θ, zodat (32) wordt:
(33) log(cos θ + i∙sin θ) = i∙(θ + 2kπ), k ∈ Ζ
Dit betekent dat we kennelijk aan de logaritme van een complex getal geen eenduidige betekenis toe kunnen kennen: de logaritme van een complex getal is slechts bepaald tot op een geheel veelvoud van 2πi. IntuÔtief is dit ook wel duidelijk uit (22). Het beeldpunt van z = cos θ + i∙sin θ bevindt zich op de eenheidscirkel, en als we θ met 2π laten toenemen of afnemen dan hebben we een volledig rondje gemaakt en bevinden we ons dus weer op hetzelfde punt, terwijl de evenredigheid van log(z) met θ zou impliceren dat de logaritme dan met 2πi zou moeten zijn toegenomen of afgenomen. Zo horen er bij elk beeldpunt van een complex getal op de eenheidscirkel dus oneindig veel waarden van log(z) die echter wel allemaal een geheel veelvoud van 2πi van elkaar verschillen.
Nemen we nu een complex getal z = x + yi ongelijk aan nul, dan weten we dat we dit altijd kunnen schrijven in de vorm z = r(cos θ + i∙sin θ) waarbij (r;θ) de poolcoŲrdinaten zijn die corresponderen met het punt (x;y) en waarbij abs(z) = |z| = r en arg(z) = θ + 2kπ, k ∈ Ζ. Nu hebben we verder op grond van de regel log(ab) = log(a) + log(b) ook:
(34) log(z) = log(r(cos θ + i∙sin θ)) = log(r) + log(cos θ + i∙sin θ),
en dus vinden we met behulp van (33):
(35) log(z) = log |z| + i∙arg(z),
waaruit weer volgt:
(36) arg(z) = -i∙log(z/|z|)
Hier heb je dus nog een formule voor arg(z). Merk op dat we in (35) en (36) arg(z) hebben, dus niet de 'hoofdwaarde' Arg(z). Immers, log(z) is slechts bepaald tot op een geheel veelvoud van 2πi evenals arg(z) slechts bepaald is tot op een geheel veelvoud van 2π. Net als bij arg(z) is het bij log(z) vaak wenselijk om met een eenduidige waarde van log(z) te kunnen werken. De - voor de hand liggende - oplossing is dan om als 'hoofdwaarde' van log(z) de waarde te nemen die in (35) correspondeert met de 'hoofdwaarde' Arg(z) van arg(z). Deze conventie wordt onder meer gevolgd door WolframAlpha en de calculator van Google.
Nog even een voorbeeld. We hadden al gevonden dat we Arg(-3 - 4i) kunnen uitdrukken als arctan(4/3) - π en als 2∙arctan(-2). Maar nu zien we dat we Arg(-3 - 4i) met behulp van (36) ook uit kunnen drukken als de 'hoofdwaarde' van -i∙log((-3 - 4i)/5). Zo hebben we drie uitdrukkingen voor Arg(-3 -4i) die er op het eerste gezicht totaal verschillend uitzien, maar die toch echt hetzelfde resultaat opleveren, zoals je in WolframAlpha kunt controleren (link: 1, 2, 3). Overigens kun je in WolframAlpha ook eenvoudig arctan(-3,-4) invoeren om Arg(-3 - 4i) te berekenen (link: 4).
quote:------------------------------------
Mijn excuses voor de vele en lange vragen. Ik heb geen leraar 'bij de hand' en tevens is wiskunde niet mijn studie of een onderdeel ervan. Ik vind het echter behoorlijke leuk en interessant en ik doe aan zelfstudie. Nadeel is dat ik alles zelf uit moet zoeken zonder leraar. Vandaar het gebruik van dit forum.
Alvast enorm bedankt!!
[ Bericht 0% gewijzigd door Riparius op 09-12-2011 12:21:23 ]


Ik heb een probleem met de volgende vraag:
"Suppose that the amplifier transfer function is given by G(s) = 1/(s+2). If the input signal to the amplifier is a sinewave with frequency of 10 Hz and with amplitude of 1, what is the amplitude of the output signal?"
De eerste stap die ik neem is:
G(s) = 1/(s+2)
G(I*omega) = 1/(I*omega+2)
En dan zit ik eigenlijk al vast. Ik weet dat de amplitude van de output abs(G(I*omega)) is. Maar hoe kan ik dit verder uitwerken?
"Suppose that the amplifier transfer function is given by G(s) = 1/(s+2). If the input signal to the amplifier is a sinewave with frequency of 10 Hz and with amplitude of 1, what is the amplitude of the output signal?"
De eerste stap die ik neem is:
G(s) = 1/(s+2)
G(I*omega) = 1/(I*omega+2)
En dan zit ik eigenlijk al vast. Ik weet dat de amplitude van de output abs(G(I*omega)) is. Maar hoe kan ik dit verder uitwerken?


Waar staan s, l en omega voor? Je kan vast wel op een of andere manier die frequentie daarin invullen.


• 1/(s+2) is volgens mij voor de laplace getransformeerde van e^(-2 t)
• i staat voor Imaginair getal (had in mijn post een kleine i moeten zijn)
• i*omega(kleine letter) is volgens mij de frequentie
• i staat voor Imaginair getal (had in mijn post een kleine i moeten zijn)
• i*omega(kleine letter) is volgens mij de frequentie


Solve the initial-value problem of the following second-order differential equation:
y''-y'-12y=0 with y(1)=0 and y'(1)=1
Krijg dan
(1) y(1)=Ae^(4)+Be^(-3)=0 en
(2) y'(1)=1=Ae^(4x+4)-Be^(3-3x)
Met A en B constanten die ik nu moet bepalen..
Dus als stelsel vergelijkingen:
Ae^4+Be^(-3) = 0
Ae^8+B = 1
Of: (bovenste maal e^3)
Ae^7+B=0
Ae^8+B=1
En toen zat ik vast
y''-y'-12y=0 with y(1)=0 and y'(1)=1
Krijg dan
(1) y(1)=Ae^(4)+Be^(-3)=0 en
(2) y'(1)=1=Ae^(4x+4)-Be^(3-3x)
Met A en B constanten die ik nu moet bepalen..
Dus als stelsel vergelijkingen:
Ae^4+Be^(-3) = 0
Ae^8+B = 1
Of: (bovenste maal e^3)
Ae^7+B=0
Ae^8+B=1
En toen zat ik vast


Je kan volgens mij gewoon die laatste twee vergelijkingen van elkaar aftrekken, dan kan je A bepalen. Daarna kan je via ťťn van de twee nog B bepalen.
The biggest argument against democracy is a five minute discussion with the average voter.


Ja en dan krijg je Ae^8-Ae^7=1, ofwel A=1/(e^8-e^7)quote:Op woensdag 30 november 2011 17:02 schreef M.rak het volgende:
Je kan volgens mij gewoon die laatste twee vergelijkingen van elkaar aftrekken, dan kan je A bepalen. Daarna kan je via ťťn van de twee nog B bepalen.
Wat niet klopt..


De afgeleide van je functie klopt niet geloof ik. Je schrijft y'(1)=1=Ae^(4x+4)-Be^(3-3x), maar y' = 4Ae4x -3Be-3x, dus y'(1)=4Ae4 -3Be-3.quote:Op woensdag 30 november 2011 18:03 schreef Physics het volgende:
[..]
Ja en dan krijg je Ae^8-Ae^7=1, ofwel A=1/(e^8-e^7)
Wat niet klopt..
The biggest argument against democracy is a five minute discussion with the average voter.


Dit klopt natuurlijk niet 4Ae4x-3Be-3x =/= Ae4x+4-Be3-3x. Thanksquote:Op woensdag 30 november 2011 18:08 schreef M.rak het volgende:
[..]
De afgeleide van je functie klopt niet geloof ik. Je schrijft y'(1)=1=Ae^(4x+4)-Be^(3-3x), maar y' = 4Ae4x -3Be-3x, dus y'(1)=4Ae4 -3Be-3.
edit: Heb hem opgelost
[ Bericht 4% gewijzigd door Physics op 30-11-2011 19:00:47 ]


Ik heb de volgende formule met de volgende oplossing.
Echter heb ik het idee dat het antwoord andersom moet zijn.
Wie kan mij helpen?
Echter heb ik het idee dat het antwoord andersom moet zijn.
Wie kan mij helpen?
AJAX AMSTERDAM!


Als je van onderaf -2 benadert is het dus -2.000...0001quote:Op donderdag 1 december 2011 14:32 schreef bloodysunday het volgende:
Ik heb de volgende formule met de volgende oplossing.
Echter heb ik het idee dat het antwoord andersom moet zijn.
[ afbeelding ]
Wie kan mij helpen?
Dus wat krijg je dan?
[ Bericht 2% gewijzigd door Physics op 01-12-2011 15:15:48 ]


dan krijg je -2,0000000000000001 + 2 = -0,0000000000000001
Is dan pijltje naar boven van onder benaderen, en pijltje naar beneden van boven benaderen? Zo ja, dan staat het ergens anders fout in de uitwerkingen. Waardoor ik dus door de war ben geraakt.
Is dan pijltje naar boven van onder benaderen, en pijltje naar beneden van boven benaderen? Zo ja, dan staat het ergens anders fout in de uitwerkingen. Waardoor ik dus door de war ben geraakt.
AJAX AMSTERDAM!


Ja pijltje omhoog is van de onderkant benaderenquote:Op donderdag 1 december 2011 15:29 schreef bloodysunday het volgende:
dan krijg je -2,0000000000000001 + 2 = -0,0000000000000001
Is dan pijltje naar boven van onder benaderen, en pijltje naar beneden van boven benaderen? Zo ja, dan staat het ergens anders fout in de uitwerkingen. Waardoor ik dus door de war ben geraakt.


Is het youtube-kanaal van Khanacademy niet handig voor in de OP? Persoonlijk helpen die filmpjes mij heel erg, en het behandelt van niveau groep 3 tot universiteit.
÷zil | Ki SY| Son HM| Lee SW| Taeguk Warriors|


Op universitair niveau zijn er niet eens zo gek veel filmpjes. Gelukkig zijn er daarvoor weer diverse andere filmpjes, o.a. waarop hele colleges zijn opgenomen.


Klopt, ik bedoelde het begin/propedeuse van universiteit, wat natuurlijk ook afhankelijk is van de studie. Maar dan nog is het een erg breed spectrum met behulpzame filmpjesquote:Op donderdag 1 december 2011 18:07 schreef twaalf het volgende:
Op universitair niveau zijn er niet eens zo gek veel filmpjes. Gelukkig zijn er daarvoor weer diverse andere filmpjes, o.a. waarop hele colleges zijn opgenomen.
Hij heeft al ongeveer 120 filmpjes onder "Calculus", 90% daarvan is hoger dan VWO Wiskunde B niveau, dus dat is alsnog vrij veel
[ Bericht 1% gewijzigd door Thas op 01-12-2011 18:15:01 ]
÷zil | Ki SY| Son HM| Lee SW| Taeguk Warriors|


Voor eerstejaars wiskunde vakken kan het nog best handig zijn ja. Ik heb het toen zelf gebruikt voor lineaire algebra.quote:Op donderdag 1 december 2011 18:10 schreef Thas het volgende:
[..]
Klopt, ik bedoelde het begin/propedeuse van universiteit, wat natuurlijk ook afhankelijk is van de studie. Maar dan nog is het een erg breed spectrum met behulpzame filmpjes
Hij heeft al ongeveer 120 filmpjes onder "Calculus", 90% daarvan is hoger dan VWO Wiskunde B niveau, dus dat is alsnog vrij veel


Als je een tekenoverzicht van teller, noemer en f(x) (in die volgorde!!) onder elkaar had gezet, was het naar alle waarschijnlijkheid in 1 keer duidelijk gewordenquote:Op donderdag 1 december 2011 14:32 schreef bloodysunday het volgende:
Ik heb de volgende formule met de volgende oplossing.
Echter heb ik het idee dat het antwoord andersom moet zijn.
[ afbeelding ]
Wie kan mij helpen?
T(f(x)): ++++++++++++2+++++++++++++
____________________________________
x......................................0..........................
N(f(x)): - - - - - - * +++++++++++++++++++
_____________________________________
x.......................(-2).......0.............................
f(x):
lim→0 - - - - - - - lim↓-∞ * lim↑∞ ++++++ 2 ++++++++++++ lim→0
__________________________________________________________
lim → -∞ ....................... -2 .........................0................................lim→∞
[ Bericht 5% gewijzigd door VanishedEntity op 01-12-2011 23:06:43 (formatting issues :') ) ]


Ooh nu zie ik het!quote:Op donderdag 1 december 2011 23:03 schreef VanishedEntity het volgende:
[..]
Als je een tekenoverzicht van teller, noemer en f(x) (in die volgorde!!) onder elkaar had gezet, was het naar alle waarschijnlijkheid in 1 keer duidelijk geworden.
T(f(x)): ++++++++++++2+++++++++++++
____________________________________
x......................................0..........................
N(f(x)): - - - - - - * +++++++++++++++++++
_____________________________________
x.......................(-2).......0.............................
f(x):
lim→0 - - - - - - - lim↓-∞ * lim↑∞ ++++++ 2 ++++++++++++ lim→0
__________________________________________________________
lim → -∞ ....................... -2 .........................0................................lim→∞
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.


Tekenoverzicht in simpel tekst format: de juiste plaatjes voor de functie die Bloodysunday postte kon ik niet 1,2,3 op een andere manier uit de mouw toveren. De legenda is:
T(f(x)) = de teller van f(x)
N(f(x)) = de noemer van f(x)
f(x) oftewel y; spreekt voor zich
* = y-waarde niet gedefinieerd voor de betreffende x-waarde.
lim = limiet
(-) ∞ = (min) oneindig met ↓, ↑, → om de limiet in kwestie van boven, van onderen resp. zonder specifieke richting te benaderen.
Boven de streep staan de tekens (plus of min), belangrijke functiewaarden, en * voor niet gedefinieerd, voor teller, noemer of f(x). Onder de streep staan de x-waarden die relevant zijn. De puntjes zijn er alleen om de formatting nog enigzins beschaafd te houden.
zie "tekenoverzicht" op wikipedia voor verdere uitleg.
[ Bericht 0% gewijzigd door VanishedEntity op 02-12-2011 05:10:27 ]
T(f(x)) = de teller van f(x)
N(f(x)) = de noemer van f(x)
f(x) oftewel y; spreekt voor zich
* = y-waarde niet gedefinieerd voor de betreffende x-waarde.
lim = limiet
(-) ∞ = (min) oneindig met ↓, ↑, → om de limiet in kwestie van boven, van onderen resp. zonder specifieke richting te benaderen.
Boven de streep staan de tekens (plus of min), belangrijke functiewaarden, en * voor niet gedefinieerd, voor teller, noemer of f(x). Onder de streep staan de x-waarden die relevant zijn. De puntjes zijn er alleen om de formatting nog enigzins beschaafd te houden.
zie "tekenoverzicht" op wikipedia voor verdere uitleg.
[ Bericht 0% gewijzigd door VanishedEntity op 02-12-2011 05:10:27 ]


Zij A,B,C onafhankelijk exponentieel verdeeld met parameters 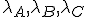 . Bereken E(max(A,B,C)).
. Bereken E(max(A,B,C)).
Ik dacht
E(max(A,B,C)) = E(max(A,B,C) | A<B<C) P(A<B<C) + E(max(A,B,C) | B<A<C) P(B<A<C) + ... + ...
en zo ga ik alle volgordes van A,B,C af. De kans P(A<B<C) heb ik al bepaald:
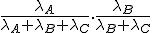 .
.
Alle andere benodigde kansen volgen hieruit door de letters A,B,C te verwisselen.
Verder weet je dat gegeven A<B<C dat max(A,B,C) = C. Dus E(max(A,B,C) | A<B<C) = E(C) = 1/lambda_C, etc. Dus op deze manier kan je die hele som berekenen.
Klopt dit en/of is er misschien een snellere methode?
[ Bericht 11% gewijzigd door thenxero op 03-12-2011 15:25:08 ]
Ik dacht
E(max(A,B,C)) = E(max(A,B,C) | A<B<C) P(A<B<C) + E(max(A,B,C) | B<A<C) P(B<A<C) + ... + ...
en zo ga ik alle volgordes van A,B,C af. De kans P(A<B<C) heb ik al bepaald:
Alle andere benodigde kansen volgen hieruit door de letters A,B,C te verwisselen.
Verder weet je dat gegeven A<B<C dat max(A,B,C) = C. Dus E(max(A,B,C) | A<B<C) = E(C) = 1/lambda_C, etc. Dus op deze manier kan je die hele som berekenen.
Klopt dit en/of is er misschien een snellere methode?
[ Bericht 11% gewijzigd door thenxero op 03-12-2011 15:25:08 ]


Het eerste stuk klopt, maar er zijn wel zes permutaties. Als je weet dat A<B<C dan weet je meer over C, namelijk dat hij 'wel groot zal zijn'. Dus niet E(max(A,B,C) | A<B<C) = E(C).
Ik zou hem zo doen: definieer X = max{A,B}. Bepaal de verdeling van X. Dan definieer je Y = MAX{X,C}. Dan Y = max{A,B,C], en van Y is de verdeling makkelijk te bepalen.
Ik zou hem zo doen: definieer X = max{A,B}. Bepaal de verdeling van X. Dan definieer je Y = MAX{X,C}. Dan Y = max{A,B,C], en van Y is de verdeling makkelijk te bepalen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ja er zijn er inderdaad 6, maar ik had geen zin om alle permutaties uit te schrijven.quote:Op zaterdag 3 december 2011 16:22 schreef GlowMouse het volgende:
Het eerste stuk klopt, maar er zijn wel zes permutaties. Als je weet dat A<B<C dan weet je meer over C, namelijk dat hij 'wel groot zal zijn'. Dus niet E(max(A,B,C) | A<B<C) = E(C).
Ik zou hem zo doen: definieer X = max{A,B}. Bepaal de verdeling van X. Dan definieer je Y = MAX{X,C}. Dan Y = max{A,B,C], en van Y is de verdeling makkelijk te bepalen.
Als je weet dat A<B<C dan weet je dat max(A,B,C)=C. Dus dan heb je wel E(max(A,B,C) | A<B<C) = E(C|A<B<C). Ik zie nu dat dat inderdaad niet hetzelfde is als E(C).
Het lijkt me niet handig om met maxima te gaan werken, want die hebben geen handige verdeling (in tegenstelling tot de minima). (vorige keer deden we dat verkeerd).


De verdeling van x is tochquote:Op zaterdag 3 december 2011 16:22 schreef GlowMouse het volgende:
Het eerste stuk klopt, maar er zijn wel zes permutaties. Als je weet dat A<B<C dan weet je meer over C, namelijk dat hij 'wel groot zal zijn'. Dus niet E(max(A,B,C) | A<B<C) = E(C).
Ik zou hem zo doen: definieer X = max{A,B}. Bepaal de verdeling van X. Dan definieer je Y = MAX{X,C}. Dan Y = max{A,B,C], en van Y is de verdeling makkelijk te bepalen.


Ah, was in de war met minima, maxima gaat inderdaad makkelijk met de cdf.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dat kan je inderdaad wel gaan doen, maar de bedoeling van de opgave is dat je handig conditioneert. De opgave is als volgt opgebouwd:
Bereken:
(a) P(A<B<C)
(b) P(A<B | max(A,B,C) = C)
(c) E(max{A,B,C} | A<B<C)
(d) E(max{A,B,C})
(a) en (b) heb ik nu, maar nu nog (c) en (d). Als je (c) hebt dan is (d) makkelijk, maar ik had (c) dus eerst fout gedaan.
E(max{A,B,C} | A<B<C) = E(C | A<B<C) = ??
Bereken:
(a) P(A<B<C)
(b) P(A<B | max(A,B,C) = C)
(c) E(max{A,B,C} | A<B<C)
(d) E(max{A,B,C})
(a) en (b) heb ik nu, maar nu nog (c) en (d). Als je (c) hebt dan is (d) makkelijk, maar ik had (c) dus eerst fout gedaan.
E(max{A,B,C} | A<B<C) = E(C | A<B<C) = ??


Misschien kun je iets met geheugenloosheid.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Geheugenloosheid wil zeggen dat P(X>t+s | X>s) = P(X > t), voor alle t,s>=0.
Ik weet niet hoe ik dat kan vertalen in iets met verwachtingswaardes. IntuÔtief zou ik denken dat E(X | X>t) = E(X) + t maar ik weet niet of dit klopt.
Ik weet niet hoe ik dat kan vertalen in iets met verwachtingswaardes. IntuÔtief zou ik denken dat E(X | X>t) = E(X) + t maar ik weet niet of dit klopt.


Dus
E(C | A<B<C) = E(C | A<C, B<C, A<B) = E(C | A<C, B<C) = E(C | A<C) + B = E(C) + A + B.
Maar daar gaat ook weer iets mis want vanwege de law of total expectation: E(C) = E(C) + E(A) + E(B).
E(C | A<B<C) = E(C | A<C, B<C, A<B) = E(C | A<C, B<C) = E(C | A<C) + B = E(C) + A + B.
Maar daar gaat ook weer iets mis want vanwege de law of total expectation: E(C) = E(C) + E(A) + E(B).


Ja maar dat is niet leuk en niet de bedoeling van de opgave. Het schijnt te kunnen zonder een enkele integraal te hoeven berekenen.


Kan ik in dit topic ook een vraag stellen hoe ik een Bode plot (phase,amp/freq) naar een transfer functie moet omzetten? Of kan ik daar beter voor bij een ander topic zijn?


De ‘quality control manager’ wil op basis van een aselecte steekproef van omvang
n de gemiddelde levensduur (in uren) van gloeilampen met een betrouwbaarheid
van 95% schatten waarbij de totale lengte van het betrouwbaarheidsinterval niet
groter mag zijn dan 20 uur. Uit eerdere onderzoeken is reeds bekend dat de standaardafwijking
van de levensduren bij lampen van dit type gelijk is aan 60 uur.
De steekproefomvang n die voor dit schattingsprobleem nodig is, is gelijk aan:
______ (numerieke waarde).
het antwoord is 139.
weet iemand hoe je aan komt?
bvb
n de gemiddelde levensduur (in uren) van gloeilampen met een betrouwbaarheid
van 95% schatten waarbij de totale lengte van het betrouwbaarheidsinterval niet
groter mag zijn dan 20 uur. Uit eerdere onderzoeken is reeds bekend dat de standaardafwijking
van de levensduren bij lampen van dit type gelijk is aan 60 uur.
De steekproefomvang n die voor dit schattingsprobleem nodig is, is gelijk aan:
______ (numerieke waarde).
het antwoord is 139.
weet iemand hoe je aan komt?
bvb
J


Hmm, zit wat te lezen over de Lagrangemultiplier maar snap er niet veel van.
Ik heb de volgende functie: f(x,y)=x^½ y^⅕
Waarbij x≥0 en y≥0. Verder heb ik de constraint 3x+4y=11.
Je krijgt nu dus:
x^½ y^⅕ - λ(3x+4y-11)=0
F'(x)=0.5x^-0.5 y^0.2 -3λ
F'(y)=0.2y^-0.8 x^0.5 -4λ
Hoe verder?
Ik heb de volgende functie: f(x,y)=x^½ y^⅕
Waarbij x≥0 en y≥0. Verder heb ik de constraint 3x+4y=11.
Je krijgt nu dus:
x^½ y^⅕ - λ(3x+4y-11)=0
F'(x)=0.5x^-0.5 y^0.2 -3λ
F'(y)=0.2y^-0.8 x^0.5 -4λ
Hoe verder?
It's 106 miles to Chicago, we've got a full tank of gas, half a pack of cigarettes, its dark, and we're wearing sunglasses. Hit it.


F'(x)=0.5x^-0.5 y^0.2 -3λ = 0 en F'(y)=0.2y^-0.8 x^0.5 -4λ = 0 stellen,quote:Op zondag 4 december 2011 15:58 schreef TJV het volgende:
Hmm, zit wat te lezen over de Lagrangemultiplier maar snap er niet veel van.
Ik heb de volgende functie: f(x,y)=x^½ y^⅕
Waarbij x≥0 en y≥0. Verder heb ik de constraint 3x+4y=11.
Je krijgt nu dus:
x^½ y^⅕ - λ(3x+4y-11)=0
F'(x)=0.5x^-0.5 y^0.2 -3λ
F'(y)=0.2y^-0.8 x^0.5 -4λ
Hoe verder?
dan beiden in labdaa uitdrukken en dat aan elkaar gelijk stellen.
Dit oplossen in x = iets met y.
Die x of y invullen in de restrictie en daar is je oplossing.
http://www.wolframalpha.com/input/?i=max+x^0.5y^0.2+%2C+3x%2B4y%3D11
[ Bericht 4% gewijzigd door Fingon op 04-12-2011 16:55:35 ]
Beneath the gold, bitter steel


Ik kom bij F'(x) tot x^-0.5=-2y^-0.2 +6λ, klopt dat? Volgens mij doe ik iets ongelofelijk fout.quote:Op zondag 4 december 2011 16:42 schreef Fingon het volgende:
[..]
F'(x)=0.5x^-0.5 y^0.2 -3λ = 0 en F'(y)=0.2y^-0.8 x^0.5 -4λ = 0 stellen,
dan beiden in labdaa uitdrukken en dat aan elkaar gelijk stellen.
Dit oplossen in x = iets met y.
Die x of y invullen in de restrictie en daar is je oplossing.
It's 106 miles to Chicago, we've got a full tank of gas, half a pack of cigarettes, its dark, and we're wearing sunglasses. Hit it.


Als je die 2(F'(x) en F'(y) ) aan elkaar gelijk stelt zou eruit moeten komen y = 3x/10quote:Op zondag 4 december 2011 16:49 schreef TJV het volgende:
[..]
Ik kom bij F'(x) tot x^-0.5=-2y^-0.2 +6λ, klopt dat? Volgens mij doe ik iets ongelofelijk fout.
F'(x)=0.5x^-0.5 y^0.2 -3λ = 0 => λ = (1/6)*x^-0.5 y^0.2
F'(y)=0.2y^-0.8 x^0.5 -4λ = 0 => λ = (1/20)*y^-0.8 x^0.5
F'(λ) = -3x - 4y +11 = 0
Deze drie oplossen.
[ Bericht 5% gewijzigd door Fingon op 04-12-2011 17:03:50 ]
Beneath the gold, bitter steel


Nee, dat krijg je niet. Je definieert m.b.v. de Lagrange multiplier een Lagrange functie van drie je variabelen x,y, λ, als volgt:quote:Op zondag 4 december 2011 15:58 schreef TJV het volgende:
Hmm, zit wat te lezen over de Lagrangemultiplier maar snap er niet veel van.
Ik heb de volgende functie: f(x,y)=x^½ y^⅕
Waarbij x≥0 en y≥0. Verder heb ik de constraint 3x+4y=11.
Je krijgt nu dus:
x^½ y^⅕ - λ(3x+4y-11)=0
L(x,y,λ) = x½ y⅕ - λ(3x+4y-11)
Vervolgens moeten de drie partiŽle afgeleiden van deze functie naar x,y en λ nul zijn, wat dus drie vergelijkingen in drie onbekenden oplevert. Het is niet zo dat de functiewaarde zelf nul zou moeten zijn zoals jij beweert. Kijk even hier.


Bekende sigma, dusquote:Op zondag 4 december 2011 09:57 schreef jimmy2211 het volgende:
De ‘quality control manager’ wil op basis van een aselecte steekproef van omvang
n de gemiddelde levensduur (in uren) van gloeilampen met een betrouwbaarheid
van 95% schatten waarbij de totale lengte van het betrouwbaarheidsinterval niet
groter mag zijn dan 20 uur. Uit eerdere onderzoeken is reeds bekend dat de standaardafwijking
van de levensduren bij lampen van dit type gelijk is aan 60 uur.
De steekproefomvang n die voor dit schattingsprobleem nodig is, is gelijk aan:
______ (numerieke waarde).
het antwoord is 139.
weet iemand hoe je aan komt?
bvb
De lengte van dat interval is


Aha, snappie. Riparius ook bedankt. Nog eentje voor de checkcheckdubbelcheck?quote:Op zondag 4 december 2011 16:56 schreef Fingon het volgende:
[..]
Als je die 2(F'(x) en F'(y) ) aan elkaar gelijk stelt zou eruit moeten komen y = 3x/10
F'(x)=0.5x^-0.5 y^0.2 -3λ = 0 => λ = (1/6)*x^-0.5 y^0.2
F'(y)=0.2y^-0.8 x^0.5 -4λ = 0 => λ = (1/20)*y^-0.8 x^0.5
F'(λ) = -3x - 4y +11 = 0
Deze drie oplossen.
C(x,y)=4x^2+4y^2+4xy+4 en de constraint=x+y=6
F'x=8x+4y-λ --> λ=8x+4y
F'y=8y=4x-λ --> λ=8y+4x
Klopt dat? Dat zou betekenen dat x=y en dan snap ik het niet meer.
It's 106 miles to Chicago, we've got a full tank of gas, half a pack of cigarettes, its dark, and we're wearing sunglasses. Hit it.


Godskolere wat ben ik dom.
Ok, we hebben gevonden dat x=y=3. Blij dat ik al zover kom, maar het antwoord heeft te maken met de shadow price. In mijn boek staat een uitleg waar ik niet uitkom, hoe reken ik dat kreng uit?
Ok, we hebben gevonden dat x=y=3. Blij dat ik al zover kom, maar het antwoord heeft te maken met de shadow price. In mijn boek staat een uitleg waar ik niet uitkom, hoe reken ik dat kreng uit?
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Hmm, ik lees dat de schaduwprijs de waarde van lambda is in het optimale punt. invoeren in bijvoorbeeld F'x geeft dan 36, klopt dat?
[ Bericht 4% gewijzigd door TJV op 04-12-2011 17:33:17 ]It's 106 miles to Chicago, we've got a full tank of gas, half a pack of cigarettes, its dark, and we're wearing sunglasses. Hit it.


En helaas klopte dat antwoord niet, wat het wel is kreeg ik niet te zien. Leuk, die oefentestjes. 
It's 106 miles to Chicago, we've got a full tank of gas, half a pack of cigarettes, its dark, and we're wearing sunglasses. Hit it.


Misschien -36 dan, staat me iets van bij dat het van belang was of je je restrictie erbij optelde of aftrok, afhankelijk van de interpretatie.


Ik ga er nog maar eens wat over lezen. 
It's 106 miles to Chicago, we've got a full tank of gas, half a pack of cigarettes, its dark, and we're wearing sunglasses. Hit it.


Simpel vraagje:
Waarom moet je delen door wortel 12 om de standaarddeviatie te krijgen? Dit kwam ik meerdere keren tegen, maar ik heb nergens gezien waarom dat zo is.
bedankt.
Waarom moet je delen door wortel 12 om de standaarddeviatie te krijgen? Dit kwam ik meerdere keren tegen, maar ik heb nergens gezien waarom dat zo is.
bedankt.


En de variantie is (b-a)≤ / 12. Dat kan je makkelijk bepalen met een momentgenererende functie.quote:Op maandag 5 december 2011 00:16 schreef thabit het volgende:
Omdat de standaarddeviatie de wortel van de variantie is.


Ok, maar ik bedoelde eigenlijk waarom "12".quote:Op maandag 5 december 2011 00:16 schreef thabit het volgende:
Omdat de standaarddeviatie de wortel van de variantie is.


Hoe zou jij de variantie willen uitrekenen?quote:Op maandag 5 december 2011 00:19 schreef Warren het volgende:
[..]
Ok, maar ik bedoelde eigenlijk waarom "12".


Ongelooflijk, wat een post! Hartelijk, hartelijk, hartelijk, hartelijk, hartelijk dank!!!! Ik stel het enorm op prijs en het heeft erg veel geholpen. Ik heb het zojuist goed bestudeerd en dingen goed in m'n gedachten voorgesteld. Ik heb het voor de zekerheid ook uitgeprint en als aantekening in m'n mapje gestopt. Je uitleg is uitstekend! Hartelijk dank voor de tijd en moeite!quote:
Je hebt tevens een grote interesse bij me opgewekt in complexe getallen. Ik kan het overgrote deel van je uitleg goed volgen als ik er goed voor ga zitten, maar ik merk dat ik oefening nodig heb om snel en goed met het onderwerp overweg te kunnen.
Ik zit er daarom aan te denken een boek aan te schaffen die specifiek over complexe getallen gaat en deze van het begin tot in de diepte behandeld, aangevuld met vele oefeningen.
Ken jij wellicht boeken over dit onderwerp die de theorie goed uitleggen en voldoende oefeningen/opgaven bevatten? (taal gaat bij voorkeur uit naar Engels, maar Nederlands is ook goed
Ik vind het knap dat je zoveel over het onderwerp weet! Ik wou dat ik ook je kennis had!
Nogmaals hartelijk dank voor je zeer uitgebreide uitleg!


quote:Op maandag 5 december 2011 00:21 schreef thabit het volgende:
[..]
Hoe zou jij de variantie willen uitrekenen?
Zo heb ik het gedaan. Ik ben nu een oefenboek aan het doorbladeren voor mijn tentamen, en een vergelijkbare opgave kwam ook nog eens voor:
Hier weer delen door wortel 12. Mij is echter totaal niet duidelijk waarom je dat doet (waarschijnlijk kom ik een of andere kennis tekort) of dit is een vaste formule


Ten eerste klopt die n-1 niet, dat moet een n zijn. Maar in dit geval hebben we niet eens een n. We hebben een continue stochast. Een integraal is dus op z'n plaats hier.quote:Op maandag 5 december 2011 00:37 schreef Warren het volgende:
[..]
[ afbeelding ]
Zo heb ik het gedaan. Ik ben nu een oefenboek aan het doorbladeren voor mijn tentamen, en een vergelijkbare opgave kwam ook nog eens voor:
[ afbeelding ]
Hier weer delen door wortel 12. Mij is echter totaal niet duidelijk waarom je dat doet (waarschijnlijk kom ik een of andere kennis tekort) of dit is een vaste formule


Oh ja bedankt, natuurlijk, dit is een continue variabelequote:Op maandag 5 december 2011 00:39 schreef thabit het volgende:
[..]
Ten eerste klopt die n-1 niet, dat moet een n zijn. Maar in dit geval hebben we niet eens een n. We hebben een continue stochast. Een integraal is dus op z'n plaats hier.
Maar waarom is het niet n-1 voor die formule van variantie? In al mijn boeken wordt n-1 gebruikt en niet n.


Het is toegestaan om een onderscheid te maken tussen s en sigma. De definitie daar is die van s. Voor sigma is een hele andere definitie, namelijk...


mensen die het verschil niet inzien tussen kansrekening en statistiekquote:Op maandag 5 december 2011 00:44 schreef twaalf het volgende:
Het is toegestaan om een onderscheid te maken tussen s en sigma. De definitie daar is die van s. Voor sigma is een hele andere definitie, namelijk...
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dat ligt deels aan de statistici zelf... wie noemt er nou twee geheel verschillende begrippen allebei variantie. 


Als U ~ Uniform(a,b), danquote:Op maandag 5 december 2011 00:37 schreef Warren het volgende:
[..]
[ afbeelding ]
Zo heb ik het gedaan. Ik ben nu een oefenboek aan het doorbladeren voor mijn tentamen, en een vergelijkbare opgave kwam ook nog eens voor:
[ afbeelding ]
Hier weer delen door wortel 12. Mij is echter totaal niet duidelijk waarom je dat doet (waarschijnlijk kom ik een of andere kennis tekort) of dit is een vaste formule
Nu jij weer.


Var(Uniform) = (b-a)^2 / 12 dus Std = sqrt(Var) = b-a/12
TE bepalen zoals hierboven getoond of kijk hier even bij moment-generating functions voor een andere manier.
Ik heb zelf ook nog een vraagje: Is deze Ito integraal correct berekend? (Bs is de Brownian motion).
TE bepalen zoals hierboven getoond of kijk hier even bij moment-generating functions voor een andere manier.
Ik heb zelf ook nog een vraagje: Is deze Ito integraal correct berekend? (Bs is de Brownian motion).
Beneath the gold, bitter steel


Zij L een taal. Laat zien dat de cardinaliteit van {L-formules} gelijk aan max{ omega, |L|}.
Hoe pak ik dit aan?
Hoe pak ik dit aan?


Ik begrijp niet wat je hier doet. Als B een functie is van s kun je ∫0t[B(s)]2∙dB schrijven als ∫0t[B(s)]2∙(dB/ds)∙ds = ∫0t[B(s)]2∙B'(s)∙ds, dus wat krijg je dan?quote:Op maandag 5 december 2011 01:39 schreef Fingon het volgende:
Ik heb zelf ook nog een vraagje: Is deze Ito integraal correct berekend? (Bs is de Brownian motion).
[ afbeelding ]


Hoe zijn de begrippen 'taal' en L-formule bij jou gedefinieerd?quote:Op maandag 5 december 2011 20:18 schreef thenxero het volgende:
Zij L een taal. Laat zien dat de cardinaliteit van {L-formules} gelijk aan max{ omega, |L|}.
Hoe pak ik dit aan?


B is ook een functie van omega, dus dat gaat niet op.quote:Op maandag 5 december 2011 20:29 schreef Riparius het volgende:
[..]
Ik begrijp niet wat je hier doet. Als B een functie is van s kun je ∫0t[B(s)]2∙dB schrijven als ∫0t[B(s)]2∙(dB/ds)∙ds = ∫0t[B(s)]2∙B'(s)∙ds, dus wat krijg je dan?


Een taal bestaat uit constantes, functiesymbolen en relatiesymbolen.quote:Op maandag 5 december 2011 20:31 schreef thabit het volgende:
[..]
Hoe zijn de begrippen 'taal' en L-formule bij jou gedefinieerd?
Een L-formule is inductief gedefinieerd:
- (t=s) is een L-formule als t en s termen van L zijn
- R(t1,...,tn) is een L-formule als t1,...,tn termen zijn
- "vals" is een formule
- L-formules zijn gesloten onder implicatie, negatie, conjunctie, disjunctie en kwantificatie
Termen zijn constantes, variabelen, of functies van termen.


|L| is de cardinaliteit van de taal L, dus de cardinaliteit van {constantes in L, functies in L, relaties in L}.


Dat een taal hooguit max(omega, |L|) formules heeft volgt uit het feit dat er hooguit max(omega, |L|) symbolen zijn en elke formule een eindige rij symbolen is. Dat er minstens zoveel formules zijn is ook makkelijk in te zien, want je kunt expliciet zoveel formules opschrijven: vals /\ ... /\ vals is een formule dus je hebt er minstens omega, t=t is een formule voor elke term, etc.


Ah dat is wel eenvoudig. Ik weet alleen niet of je vals /\ ... /\ vals als een andere formule kunt zien als vals... ze zijn immers equivalent.


Ja, dat mag denk ik wel. Een formule is een rij symbolen; twee verschillende rijen symbolen definiŽren twee verschillende formules.quote:Op maandag 5 december 2011 21:28 schreef thenxero het volgende:
Ah dat is wel eenvoudig. Ik weet alleen niet of je vals /\ ... /\ vals als een andere formule kunt zien als vals... ze zijn immers equivalent.


Inderdaad, wat een bazenpost van Riparius!
Ik heb zelf ook een probleem waar ik niet uitkom. Als iemand me een zetje in de goede richting kan geven zou ik dat zeer op prijs stellen.
Gegeven is een functie
en aan de rechterkant een getal (of 1x1 matrix, als je wil):
Ik heb zelf ook een probleem waar ik niet uitkom. Als iemand me een zetje in de goede richting kan geven zou ik dat zeer op prijs stellen.
Gegeven is een functie
en een functiequote:f(a, x) = x5 + ax = y
Nu moet het mogelijk zijn om met de kettingregel de partiŽle afgeleiden van g te bepalen, gegeven dat g differentieerbaar is. Mijn plan was omquote:g(a, y) = x
op stellen, zodatquote:f2(a, x) = (a, x5) = (a, y)
En dan beide kanten te differentiŽren en de linkerkant uit te werken met de kettingregel. Dit werkt echter niet omdat ik aan de linkerkant een rijvector krijgquote:g(f2(a, x)) = x
(het laatste is het product van een 1x2 matrix en een 2x2 matrix, wat als ik het goed heb weer een 1x2 matrix oplevert)quote:Dg(f(a, x)) = Dg(a, y)Df(a, x)
en aan de rechterkant een getal (of 1x1 matrix, als je wil):
Volgens mij is deze laatste stap trouwens niet correct (bijvoorbeeld omdat het niet duidelijk is waarvan ik precies de afgeleide neem over deze x, dus ik denk niet dat ik zomaar Dx = 1 mag stellen), maar dit was het enige wat ik kon bedenken.quote:Dx = 1
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |