SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP


waarom?quote:Op dinsdag 18 oktober 2011 21:15 schreef Hesitater het volgende:
- De halfwaardetijd is 5750 jaar, is het juist als ik dan dit zeg: N(5750) = 53660/2?
1,20547/10^4.quote:Op dinsdag 18 oktober 2011 21:26 schreef Hesitater het volgende:
Dan kom ik hierop: ln(0,5)=-k*5750 (is dit juist?)
Dan krijg ik als totale output: 1,20547
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Nou ik dacht dat als 5750 de halfwaardetijd is en je als beginwaarde 53660 hebt, het dan gehalveerd is...


Algemene oplossing voor N uitgedrukt in t en k: N(t) = 53660*e-k*t(deze formule is juist)quote:Op dinsdag 18 oktober 2011 21:26 schreef Hesitater het volgende:
Dan kom ik hierop: ln(0,5)=-k*5750 (is dit juist?)
Dan krijg ik als totale output: 1,20547
En de volgende vraag luidt: De halfwaardetijd van C14 is 5750 jaar. Bereken hieruit de waarde van k in 5 decimalen.
k =
- De halfwaardetijd is 5750 jaar, is het juist als ik dan dit zeg: N(5750) = 53660/2?
- Dan weet je dus de N en de t=5750
- Dan: 26830 = 53660*e-k*5750
Mijn vraag blijft staan, wat is de betekenis van N(t), en wat is k volgens jou voor getal, wat drukt dat uit?
Beneath the gold, bitter steel


De N(t) is hoeveel atomen we over hebben na een bepaalde tijd (t).
k ? Weet ik niet..
Oh het is de vervalsnelheid!
Dussss k*halfwaardetijd=ln(2) toch?
[ Bericht 32% gewijzigd door Hesitater op 18-10-2011 21:44:31 ]
k ? Weet ik niet..
Oh het is de vervalsnelheid!
Dussss k*halfwaardetijd=ln(2) toch?
[ Bericht 32% gewijzigd door Hesitater op 18-10-2011 21:44:31 ]


Je kunt gebruik maken van:quote:Op dinsdag 18 oktober 2011 20:55 schreef Anoonumos het volgende:
Bewijs de volgende ongelijkheid:voor alle x>0
Ik weet dat ik de middelwaarde stelling moet gebruiken, maar ik kan geen ln 0 nemen. Hoe vermijd ik dit?
ln x = ∫1x dt/t
Aangezien 1/t monotoon dalend is voor t > 0 heb je dan:
(x-1)/x ≤ ln x ≤ x-1
De gelijkheid geldt alleen voor x = 1.


Bij een onderzoek naar de relatie tussen automerken en rijgedrag is de snelheid gemeten van een aantal auto’s op een weg waar 80 km/h mag worden gereden. Er zijn voor elk automerk 22 waarnemingen gedaan, samengevat levert dat:
Automerk n snelheid gemiddeld st.deviatie minimum maximum
Opel 22 76,29 4,611 70 87
Audi 22 83,42 5,492 62 103
Toyota 22 87,25 3,879 79 94
Peugeot 22 79,84 5,012 62 90
Totaal 88 81,70 6,239 62 103
a. Maak de bijbehorende variantie-analyse (ANOVA-)tabel (vermeld uw eindantwoord in het voorgestructureerde kader; gebruik het eerste kader voor uw berekeningen). Alle antwoorden tot op 2 decimalen.
Summed Square of Groups.
(4,611)-(6,239) ^ 2 = 2.65
(5,492)-(6,239) ^ 2 = 0.56
(3.879)-(6,239) ^ 2 = 5.70
(5,012)-(6,239) ^ 2 = 1.51
2.65+0.56+5.70+1.51 = 10.42
SSG=10.42
Summed Square of total
N = 88
Xbar = 81.7
Standaarddeviatie = 6.239
Squared standaarddeviatie = 38.93
N x Squared standaarddeviatie =3425.41
SST=3425.41
SSE=SST
Verder K = 4 en dan kan je alles zo invullen in een ANOVA tabel. Maar mijn vraag is nu eigenlijk of mijn SST en SSG goed berekend zijn...
Automerk n snelheid gemiddeld st.deviatie minimum maximum
Opel 22 76,29 4,611 70 87
Audi 22 83,42 5,492 62 103
Toyota 22 87,25 3,879 79 94
Peugeot 22 79,84 5,012 62 90
Totaal 88 81,70 6,239 62 103
a. Maak de bijbehorende variantie-analyse (ANOVA-)tabel (vermeld uw eindantwoord in het voorgestructureerde kader; gebruik het eerste kader voor uw berekeningen). Alle antwoorden tot op 2 decimalen.
Summed Square of Groups.
(4,611)-(6,239) ^ 2 = 2.65
(5,492)-(6,239) ^ 2 = 0.56
(3.879)-(6,239) ^ 2 = 5.70
(5,012)-(6,239) ^ 2 = 1.51
2.65+0.56+5.70+1.51 = 10.42
SSG=10.42
Summed Square of total
N = 88
Xbar = 81.7
Standaarddeviatie = 6.239
Squared standaarddeviatie = 38.93
N x Squared standaarddeviatie =3425.41
SST=3425.41
SSE=SST
Verder K = 4 en dan kan je alles zo invullen in een ANOVA tabel. Maar mijn vraag is nu eigenlijk of mijn SST en SSG goed berekend zijn...


f(x) = ln(x+1) - x + x²/2 + x³/6
Prove that: f ' (x) = x²-x³
..............................2x + 1
Ik kom er maar niet uit, zonet een uur naar lopen staren terwijl ik normaliter nooit moeite heb met afgeleiden.
x²/2 en x³/6 leidt je volgens mij zo af: 1/2 * 2x = x en 1/6 * 3x² = 0,5x² (of x²/2)
ln(x+1) = 1/x+1
en -x = -1
En vanaf daar geraak ik maar niet verder ..
btw vraag 2: Df (-1,+infinity) .. » Vind extreme waarden .. antw.boek geeft x=1 is maximum maar dat zie ik ook nog steeds niet.
Prove that: f ' (x) = x²-x³
..............................2x + 1
Ik kom er maar niet uit, zonet een uur naar lopen staren terwijl ik normaliter nooit moeite heb met afgeleiden.
x²/2 en x³/6 leidt je volgens mij zo af: 1/2 * 2x = x en 1/6 * 3x² = 0,5x² (of x²/2)
ln(x+1) = 1/x+1
en -x = -1
En vanaf daar geraak ik maar niet verder ..
btw vraag 2: Df (-1,+infinity) .. » Vind extreme waarden .. antw.boek geeft x=1 is maximum maar dat zie ik ook nog steeds niet.


Laten we bij het eerste beginnen:quote:Op woensdag 19 oktober 2011 17:51 schreef Sokz het volgende:
f(x) = ln(x+1) - x + x²/2 + x³/6
Prove that: f ' (x) = x²-x³
..............................2x + 1
Ik kom er maar niet uit, zonet een uur naar lopen staren terwijl ik normaliter nooit moeite heb met afgeleiden.
x²/2 en x³/6 leidt je volgens mij zo af: 1/2 * 2x = x en 1/6 * 3x² = 0,5x² (of x²/2)
ln(x+1) = 1/x+1
en -x = -1
En vanaf daar geraak ik maar niet verder ..
btw vraag 2: Df (-1,+infinity) .. » Vind extreme waarden .. antw.boek geeft x=1 is maximum maar dat zie ik ook nog steeds niet.
Je afgeleiden zijn goed, behalve dan dat je niet -x=-1 en ln(x+1)=1/x+1 moet schrijven, want dat ziet er een beetje vreemd uit. Let er wel op dat de afgeleide van ln(x+1) gelijk is aan 1/(x+1) en niet 1/x+1. Essentieel verschil!
Goed, laten we de dingen eens optellen:
-1+1/(x+1)+x+0.5x^2. Laten we alles gelijknamig maken:
(-(x+1) + 1 + x(x+1)+0.5x^2(x+1)) / (x+1)
=
(-x-1+1+x^2+x+0.5x^3+0.5x^2) / (x+1)
=
(1.5x^2 + 0.5x^3)/(x+1)
-> antwoord bij jouw vraag klopt niet. Kun je ook aan de noemer zien. Voor jouw afgeleide geldt dat deze niet gedefinieerd is voor x=-0.5, terwijl de functie op x=-0.5 prima differentieerbaar is.
vraag 2: Extreme waarde vind je door de afgeleide gelijk te stellen aan nul.
Succes


Zij P(A dissection B)=0.4, P(A dissection C)=0.5 en P(B dissection C)=0.6
Leidt af welke waarden P(A dissection B dissection C) kan aannemen.
Ik heb echt geen enkel idee wat ik hier moet doen en hoe.
[ Bericht 1% gewijzigd door Physics op 19-10-2011 21:04:30 ]
Leidt af welke waarden P(A dissection B dissection C) kan aannemen.
Ik heb echt geen enkel idee wat ik hier moet doen en hoe.
[ Bericht 1% gewijzigd door Physics op 19-10-2011 21:04:30 ]


P(B dissection C) wat?
Begin met een Venn-diagram.
Begin met een Venn-diagram.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik bedoel intersection idd  Ja ik heb een venn diagram getekend etc, maar geen idee hoe ik er daadwerkelijk aan reken. Originele post aangepast, klote toetsenbord hier werkt voor geen meter.
Ja ik heb een venn diagram getekend etc, maar geen idee hoe ik er daadwerkelijk aan reken. Originele post aangepast, klote toetsenbord hier werkt voor geen meter.


A door B door C is het grootst als de cirkels zoveel mogelijk overlappen. A door B door C is het kleinst als de cirkels weinig of zelfs niet overlappen. Dus kijk in hoeverre de cirkels kunnen overlappen.


Ja stel (A intersect B) intersect (B intersect C) intersect (B intersect C) kan dit maximaal de waarde aanneme van de kleinste kans, ofwel A intersect B = 0.4. Dus dat zou dan de maximale waarde zijn, en dat hierboven is gelijk aan A intersect B intersect C.
Nu minimaal nog
Nu minimaal nog


Klopt.
edit: vraag verkeerd gelezen
Noem de kans op de doorsnede van alledrie p. Dan is p minimaal als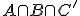 ,
, 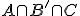 en
en 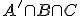 zo groot mogelijk zijn, dus weinig overlappen in p. Dan is
zo groot mogelijk zijn, dus weinig overlappen in p. Dan is 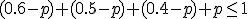 , hieruit volgt dat
, hieruit volgt dat 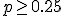 .
.
[ Bericht 89% gewijzigd door twaalf op 19-10-2011 21:25:50 ]
edit: vraag verkeerd gelezen
Noem de kans op de doorsnede van alledrie p. Dan is p minimaal als
[ Bericht 89% gewijzigd door twaalf op 19-10-2011 21:25:50 ]


Dat laatste deel had ik net nodig, thanks!quote:Op woensdag 19 oktober 2011 21:16 schreef twaalf het volgende:
Klopt.
edit: vraag verkeerd gelezen
Noem de kans op de doorsnede van alledrie p. Dan is p minimaal als,
en
zo groot mogelijk zijn, dus weinig overlappen in p. Dan is
, hieruit volgt dat
.


Zijn er nog mensen die een poging willen wagen? Want het antwoord schijnt wel te moeten kloppen (omdat sommige klasgenoten het wél voor elkaar kregen:} )quote:Op woensdag 19 oktober 2011 18:55 schreef Don_Vanelli het volgende:
[..]
Laten we bij het eerste beginnen:
Je afgeleiden zijn goed, behalve dan dat je niet -x=-1 en ln(x+1)=1/x+1 moet schrijven, want dat ziet er een beetje vreemd uit. Let er wel op dat de afgeleide van ln(x+1) gelijk is aan 1/(x+1) en niet 1/x+1. Essentieel verschil!
Goed, laten we de dingen eens optellen:
-1+1/(x+1)+x+0.5x^2. Laten we alles gelijknamig maken:
(-(x+1) + 1 + x(x+1)+0.5x^2(x+1)) / (x+1)
=
(-x-1+1+x^2+x+0.5x^3+0.5x^2) / (x+1)
=
(1.5x^2 + 0.5x^3)/(x+1)
-> antwoord bij jouw vraag klopt niet. Kun je ook aan de noemer zien. Voor jouw afgeleide geldt dat deze niet gedefinieerd is voor x=-0.5, terwijl de functie op x=-0.5 prima differentieerbaar is.
vraag 2: Extreme waarde vind je door de afgeleide gelijk te stellen aan nul.
Succes


Ik kwam er ook niet uit nee.quote:Op woensdag 19 oktober 2011 22:50 schreef twaalf het volgende:
Het is echt niet waar; Don_Vanille geeft toch een goed argument?


Ik denk sowieso dat ze die x³/6 niet als 05x² schrijven maar als x²/2 (en dan gelijsktellen krijg je 2(x+1) .. maar nog 2(x+1) =/= 2x + 1quote:Op woensdag 19 oktober 2011 23:04 schreef Fingon het volgende:
wolfram geeft dit:
dit.
Lijkt er een beetje op, wss heb je haakjes niet goed.
ik zal die wolfram eens naar mijn leraar sturen via mail. Benieuwd naar zijn antwoord.


