SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Uitzoeken hoe iets echt zit is nooit tijdsverspilling, want je leert daar iets van, in tegenstelling tot van het indrukken van wat toetsen op een calculator met als resultante het 'goede' antwoord.quote:Op donderdag 27 oktober 2011 17:54 schreef Zweefkaak het volgende:
Het zou gewoon uit te rekenen moeten zijn met een of andere formule, dus dit is een beetje tijdverspilling van elkaar
[ Bericht 0% gewijzigd door Riparius op 27-10-2011 18:35:02 ]
quote:
Je moet juist niet op zoek gaan naar de delta, maar naar de epsilon. Uiteindelijk moet je de som nemen van twee functies, en daar moet iets uitkomen dat kleiner is dan epsilon. Logisch is dan om te kijken naar. Als je uitgaat van een bepaalde epsilon waaraan f+g moet voldoen, dan kun je voor
vinden voor f en een
vinden voor g.
Heel erg bedankt!quote:
[..]
Het gaat er niet om dat je voor een 'gegeven' ε > 0 aantoont dat er zo'n δ is, maar dat je aantoont dat er voor elke ε > 0 een δ > 0 bestaat zodanig dat | f(x) - f(p) | < ε indien | x - p | < δ. Je moet dus een existentiebewijs leveren, en dat niet voor één ε > 0 maar voor elke ε > 0. In het algemeen doe je dat door te laten zien dat je bij elke ε > 0 een δ > 0 kunt construeren die aan het gestelde voldoet.
[..]
Gegeven is dat f: R ↦ R en g: R ↦ R continue functies zijn. Gevraagd wordt nu te bewijzen dat de functie F: R ↦ R gedefinieerd door F(x) = α∙f(x) + β∙g(x) met α,β > 0 eveneens continu is op R.
[knip]
Ik snap het nu stukken beter
Özil | Ki SY| Son HM| Lee SW| Taeguk Warriors|
Ik ben daar een uur mee bezig geweest, het hoofdstuk een x-aantal keer doorgespit, maar het staat er gewoon niet..quote:
[..]
Uitzoeken hoe iets echt zit is nooit tijdsverspilling, want je leert daar iets van, in tegenstelling tot van het indrukken van wat toetsen op een calculator met als resultante het 'goede' antwoord.
Je moet weten wat een cumulatieve kans is. In je tabellen staan namelijk cumulatieve kansen, die moet je geregeld omzetten in kansen op intervallen.
Afhankelijk van je tabellen staan daar voor een aantal x ofwel de kansen P(X>x) ofwel de kansen P(X<x) waarbij X normaal verdeeld is met verwachting 0 en standaardafwijking 1.
Nu ben je geïnteresseerd in bv. de kans P(1<X<3). Dan schrijf je die kans als P(X<3)-P(X<1). Die twee kansen staan in je tabel.
Afhankelijk van je tabellen staan daar voor een aantal x ofwel de kansen P(X>x) ofwel de kansen P(X<x) waarbij X normaal verdeeld is met verwachting 0 en standaardafwijking 1.
Nu ben je geïnteresseerd in bv. de kans P(1<X<3). Dan schrijf je die kans als P(X<3)-P(X<1). Die twee kansen staan in je tabel.
Je hebt volkomen gelijk, alleen ga je voorbij aan het feit dat dit een vraag is op het niveau wiskunde A van de middelbare school. Op dat niveau vliegt men wel vaker uit de bocht in het lesmateriaal.quote:Op donderdag 27 oktober 2011 16:31 schreef GlowMouse het volgende:
Je lijkt naar een antwoord toe te werken in plaats van zuiver naar de vraag te kijken.
Dat is de kans op een score van ten hoogste 23, een andere vraag.quote:
Je begrijpt dat het hier om een normaal verdeling gaat en dat alles omgerekend kan worden naar kansen, maar ik krijg namelijk antwoord 2 eruit.
z-score = (23-20) / 5 = 0,6
opzoeken in de tabel, etc
(sorry voor de dubbelpost)
Je had dat trouwens ook nog metquote:
z-score = (23-20) / 5 = 0,6
opzoeken in de tabel, etc
Dank je wel! Het is me iets duidelijker.quote:
[..]
Je kan wel berekenen wat de afgeleide is van een functie, maar je kan het niet bewijzen als je niet weet wat een limiet is. Je krijgt een kookboek aangeboden van zo en zo moet het, maar eigenlijk heb je geen idee waarom het echt zo is.
Een continue functie is informeel een functie die geen sprongen maakt, oftewel een functie die je kan tekenen zonder je pen van het papier te halen. Maar dit is natuurlijk niet echt een exacte wiskundige definitie. Je kan niet een bewijs opschrijven waarom je iets kan tekenen zonder je pen van het papier te halen... kortom: je hebt goede wiskundige definities nodig voor bewijzen.
5/wortel 9quote:
[..]
Je had dat trouwens ook nog metmoeten vermenigvuldigen.
Vraag me niet hoe, maar daar kwam ik achter... En die vraag werd bijna letterlijk gevraagd op tentamen, dus had het antwoord alvast ingevuld alvorens het te berekenen.
De volgende vraag over de vraagstelling bij een tentamen:
"Consider the system:
f1(u,v,x,y) = u^2v - u - (x^3+2y^3 = 0
f2(u,v,x,y) = e^xu - vy = 0
Derive a system of two equations for ∂u/∂x in terms of partial derivatives of f1 and f2 from which ∂u/∂x can be solved.
Note: you are not requested to solve the system.
Dus ik heb de systemen van vergelijkingen gemaakt en daarna de cramer rule toegepast om te laten zien dat ik het kan oplossen.
Ik heb echter de termen "∂f2/∂v" (de afgeleiden) gewoon zo gelaten en dus niet vervangen "-y" omdat ik het systeem toch niet hoefden op te lossen en ik het dus niet nodig vond.
Nu staat er in het antwoordmodel dat dit wel nodig is, en ik vroeg mij af of ik hiervoor punten aftrek zou mogen krijgen?
Ik heb mij tenslotte wel aan de vraag gehouden, ik heb het weergegeven in de partiële afgeleiden van f1 en f2, alleen ik heb de afgeleiden niet ingevuld.
"Consider the system:
f1(u,v,x,y) = u^2v - u - (x^3+2y^3 = 0
f2(u,v,x,y) = e^xu - vy = 0
Derive a system of two equations for ∂u/∂x in terms of partial derivatives of f1 and f2 from which ∂u/∂x can be solved.
Note: you are not requested to solve the system.
Dus ik heb de systemen van vergelijkingen gemaakt en daarna de cramer rule toegepast om te laten zien dat ik het kan oplossen.
Ik heb echter de termen "∂f2/∂v" (de afgeleiden) gewoon zo gelaten en dus niet vervangen "-y" omdat ik het systeem toch niet hoefden op te lossen en ik het dus niet nodig vond.
Nu staat er in het antwoordmodel dat dit wel nodig is, en ik vroeg mij af of ik hiervoor punten aftrek zou mogen krijgen?
Ik heb mij tenslotte wel aan de vraag gehouden, ik heb het weergegeven in de partiële afgeleiden van f1 en f2, alleen ik heb de afgeleiden niet ingevuld.
Ze vragen er toch juist om om het in termen van partial derivatives op te schrijven? Dan zou het juist fout zijn om die partial derivatives uit te rekenen.
Nog even om te illustreren:
De vraag:
Antwoord
Volgens jou is mijn antwoord goed?
[ Bericht 19% gewijzigd door JohnSpek op 29-10-2011 23:52:46 ]
De vraag:
Antwoord
Volgens jou is mijn antwoord goed?
[ Bericht 19% gewijzigd door JohnSpek op 29-10-2011 23:52:46 ]
Dat antwoord van je docent is inderdaad lichtelijk belachelijk als je niks moet uitrekenen, want daar bereken je toch echt afgeleiden.
Vrij vreemd.
Vrij vreemd.
Beneath the gold, bitter steel
@ JohnSpek, je antwoord lijkt mij gewoon correct. Gezien het niveau van de vraagstelling is het natuurlijk een triviale zaak om de afgeleiden uit te rekenen. Er wordt gevraagd naar een systeem, zodat die twee afgeleiden naar x opgelost kunnen worden. Jij geeft dat oplosbare systeem. Lijkt mij geen speld tussen te krijgen
Zitten hier mensen die stochastics and financial mathematics of een vergelijkbare master volgen? Klik dan hier.
Lijkt me niet. Ik ken deze notatie ook niet, wel de zogeheten floor en ceiling functies. Wellicht bedoel je die.quote:
Is [|x|] afronden naar dichtstbijzijnde x als element van Z (gehele getallen)?
Edit: ik zie net dat Gauss in 1808 [x] gebruikte voor floor(x), maar die notatie is nu niet meer gebruikelijk.
[ Bericht 3% gewijzigd door Riparius op 30-10-2011 15:21:34 ]
Wat bedoel je met [|x|] ?quote:
Is [|x|] afronden naar dichtsbijzijnde x als element van Z (gehele getallen)?
Dit is kennelijk een poging van Physics om double stroked brackets weer te geven. Ik zie nu dat die soms worden gebruikt voor de floor functie, maar ik zie zo gauw geen unicode daarvoor. De symbolen ⌈ ⌉ ⌊ ⌋ zijn wel vertegenwoordigd in unicode.quote:
Als hij de entier / floor function bedoelt dan is het duidelijk niet waar.
Dan geldt [|5.9|] = 5, en ligt 6 dichterbij. Ik heb het vermoeden dat hij zelf die notatie ook niet kent, anders had hij dit ook wel zelf kunnen bedenken .
Dan geldt [|5.9|] = 5, en ligt 6 dichterbij. Ik heb het vermoeden dat hij zelf die notatie ook niet kent, anders had hij dit ook wel zelf kunnen bedenken
.
Nee ik kende de notatie niet. Net gevonden dat ze de greatest integer function bedoelen. Thanks anyway. Nu lijkt de vraag triviaal.
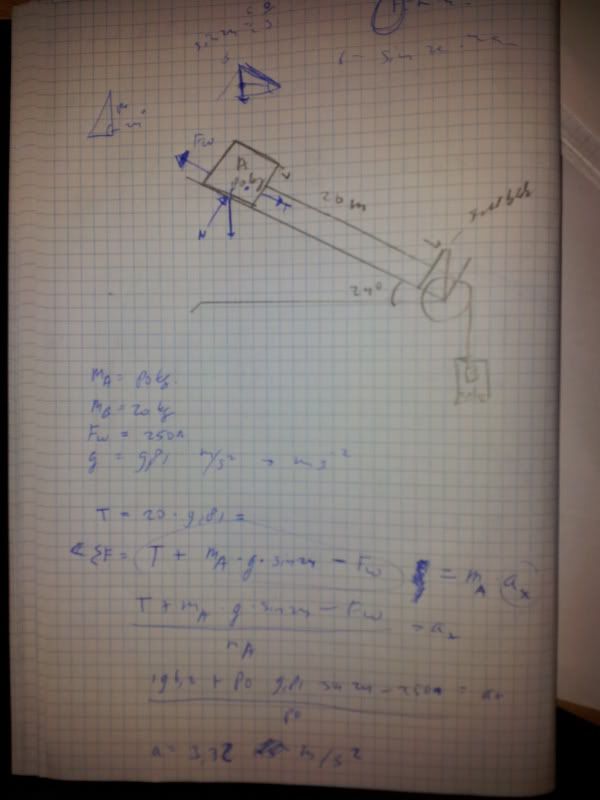
Heren , une question, gelieve mij te helpen, ik kom er zelf niet uit (al veel geprobeerd).
De opdracht met vragen:
Mijn poging op vraag 1 (weet niet of het klopt) (en heb v niet kunnen uitrekenen) (p.s. niets met integralen a.u.b. ):
Mijn poging op vraag 2:
De opdracht met vragen:
Mijn poging op vraag 1 (weet niet of het klopt) (en heb v niet kunnen uitrekenen) (p.s. niets met integralen a.u.b. ):
Mijn poging op vraag 2:
Bij a kan je v berekenen met:
s = 1/2 a t²
en dan v = a / t v=at
[ Bericht 16% gewijzigd door Anoonumos op 30-10-2011 20:38:28 ]
s = 1/2 a t²
en dan v = a / t v=at
[ Bericht 16% gewijzigd door Anoonumos op 30-10-2011 20:38:28 ]
Er werken drie krachten op het blok:
• Parallelle component van de zwaartekracht, 80gcos24 N
• Zwaartekracht van het kleine blok, 20g N
• Wrijving van 250 N
Geeft een som van ongeveer 700 N, dus een versnelling van 700/80=8 m/s^2.
• Parallelle component van de zwaartekracht, 80gcos24 N
• Zwaartekracht van het kleine blok, 20g N
• Wrijving van 250 N
Geeft een som van ongeveer 700 N, dus een versnelling van 700/80=8 m/s^2.
Die cosinus moet een sinus zijn neem ik aanquote:
Er werken drie krachten op het blok:
• Parallelle component van de zwaartekracht, 80gcos24 N
• Zwaartekracht van het kleine blok, 20g N
• Wrijving van 250 N
Geeft een som van ongeveer 700 N, dus een versnelling van 700/80=8 m/s^2.
Bij een hellingshoek van 0 graden is de parallelle component 0, en niet 80*g N.
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!
