SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Eigenlijk is dit natuurkunde. Als je de versnelling a van het blok langs de helling kent, en de lengte s van de helling (die is gegeven) dan kun je met:quote:
(1) s = ½at2
uitrekenen hoe lang het blok erover doet om beneden te komen. Daaruit bereken je dan weer met:
(2) v = at
de snelheid op het moment dat het blok onderaan de helling arriveert.
Maar je gaat me toch niet vertellen dat je dit niet wist?
http://i.imgur.com/GveY7.jpg zo had ik 'm, ben wel benieuwd of dit goed is? (nam aan dat touw massaloos was)
[ Bericht 10% gewijzigd door jabbahabba op 30-10-2011 22:14:18 ]
[ Bericht 10% gewijzigd door jabbahabba op 30-10-2011 22:14:18 ]
Hallo,
voor een inleveropdracht zijn we op zoek naar een irreducibel getal waarvan de norm niet priem is. En we komen er echt niet uit. Hulp vriendelijk gevraagd
voor een inleveropdracht zijn we op zoek naar een irreducibel getal waarvan de norm niet priem is. En we komen er echt niet uit. Hulp vriendelijk gevraagd
Zou iemand me een stapje kunnen helpen met deze opdracht? Ik weet wat de limieten van de afzonderlijke functies zijn, alleen met de samengestelde functie kom ik er niet uit...
Finally, someone let me out of my cage
Als je de functies schrijft als reeksontwikkeling zou het moeten lukken.quote:Op maandag 31 oktober 2011 17:10 schreef minibeer het volgende:
Zou iemand me een stapje kunnen helpen met deze opdracht? Ik weet wat de limieten van de afzonderlijke functies zijn, alleen met de samengestelde functie kom ik er niet uit...
[ afbeelding ]
The biggest argument against democracy is a five minute discussion with the average voter.
Ik zal er vanavond even naar kijken, *zucht* ik loop achterquote:Op maandag 31 oktober 2011 17:16 schreef M.rak het volgende:
[..]
Als je de functies schrijft als reeksontwikkeling zou het moeten lukken.
edit: ik heb net even wat gelezen over de regel van l'Hôpital, ik denk dat het daarmee wel zou moeten lukken, thanks!
[ Bericht 8% gewijzigd door minibeer op 31-10-2011 17:34:56 ]
Finally, someone let me out of my cage
Ik zou dit herschrijven als een product, en wel:quote:
Zou iemand me een stapje kunnen helpen met deze opdracht? Ik weet wat de limieten van de afzonderlijke functies zijn, alleen met de samengestelde functie kom ik er niet uit...
[ afbeelding ]
((1 - cos x)/x2)∙(sin x / x)∙(1/log(1+x)1/x))
De limiet voor x → 0 wordt dan:
½∙1∙1/log e = ½.
Mooi hè?
Je gebruikt dan wel 2 "standaardlimieten" en ik denk niet dat dat de bedoeling is. Ik zou de eerste twee termen van de 3 Taylorreeksen pakken van cos(x),sin(x) en log(1+x).quote:
[..]
Ik zou dit herschrijven als een product, en wel:
((1 - cos x)/x2)∙(sin x / x)∙(1/log(1+x)1/x))
De limiet voor x → 0 wordt dan:
½∙1∙1/log e = ½.
Mooi hè?
Ik weet niet wat 'de bedoeling' is van de opgave, dat kan alleen Minibeer beantwoorden. Maar ik zie zo dat de limiet ½ is, daar heb ik geen Taylorreeksen voor nodig.quote:
[..]
Je gebruikt dan wel 2 "standaardlimieten" en ik denk niet dat dat de bedoeling is. Ik zou de eerste twee termen van de 3 Taylorreeksen pakken van cos(x),sin(x) en log(1+x).
Dit is de hele opgave (uit een oefententamen), maar we bijvoorbeeld x/sin(x) niet als standaardlimiet gehad (dus ik denk dat je die nog afzonderlijk zou moeten bewijzen met bijvoorbeeld de regel van l'Hôpital), daardoor raakte ik een beetje in de war. Maar als ik gewoon die regel toepas, zie ik het welquote:
[..]
Ik weet niet wat 'de bedoeling' is van de opgave, dat kan alleen Minibeer beantwoorden. Maar ik zie zo dat de limiet ½ is, daar heb ik geen Taylorreeksen voor nodig.
.
Finally, someone let me out of my cage
Je moet niet de limiet van sin x / x voor x naar 0 gaan 'bewijzen' met de regel van L'Hôpital, want dan maak je gebruik van het feit dat de afgeleide van sin x naar x gelijk is aan cos x. Maar om dát te bewijzen (aan de hand van de definitie van de afgeleide) moet je weer gebruik maken van het feit dat de limiet van sin x / x voor x naar 0 gelijk is aan 1. En dus verval je zo in een cirkelredenatie.quote:
[..]
Dit is de hele opgave (uit een oefententamen), maar we bijvoorbeeld x/sin(x) niet als standaardlimiet gehad (dus ik denk dat je die nog afzonderlijk zou moeten bewijzen met bijvoorbeeld de regel van l'Hôpital), daardoor raakte ik een beetje in de war. Maar als ik gewoon die regel toepas, zie ik het wel
Ik heb er even over nagedacht, en je hebt gelijk, maar ik denk wel dat dit de manier is waarop we geacht worden dit te doen. Dan zal het wel niet volstaan als formeel bewijs, maar omdat je weet dat de regel van l'Hôpital geldt, kan je het denk ik wel gebruiken om je antwoord aannemelijk te maken. Ik zal zo even de uitwerking die ik nu heb posten, bedankt voor de hulpquote:
[..]
Je moet niet de limiet van sin x / x voor x naar 0 gaan 'bewijzen' met de regel van L'Hôpital, want dan maak je gebruik van het feit dat de afgeleide van sin x naar x gelijk is aan cos x. Maar om dát te bewijzen (aan de hand van de definitie van de afgeleide) moet je weer gebruik maken van het feit dat de limiet van sin x / x voor x naar 0 gelijk is aan 1. En dus verval je zo in een cirkelredenatie.
!
Finally, someone let me out of my cage
limx→0 ((1 - cos(x)) * sin(x)) / (x2log(1 + x)) = limx→0 (1-cos(x))/x2 * limx→0 sin(x)/x * limx→0 x/(log(1+x))
Met de regel van 'Hôpital:
limx→0 (1-cos(x))/x2 = limx→0 sin(x)/2x = limx→0 cos(x)/2 = 1/2
limx→0 sin(x)/x = limx→0 cos(x)/1 = 1
limx→0 x/log(1+x) = limx→0 1/(1+x)-1 = limx→0 1+x = 1
Dus:
limx→0 ((1 - cos(x)) * sin(x)) / (x2log(1 + x)) = 1/2 * 1 * 1 = 1/2
(zoals Riparius al opmerkte)
Sorry voor de layout, het is slecht te lezen zo, ik moet echt eens LaTeX leren
...
Met de regel van 'Hôpital:
limx→0 (1-cos(x))/x2 = limx→0 sin(x)/2x = limx→0 cos(x)/2 = 1/2
limx→0 sin(x)/x = limx→0 cos(x)/1 = 1
limx→0 x/log(1+x) = limx→0 1/(1+x)-1 = limx→0 1+x = 1
Dus:
limx→0 ((1 - cos(x)) * sin(x)) / (x2log(1 + x)) = 1/2 * 1 * 1 = 1/2
(zoals Riparius al opmerkte
)Sorry voor de layout, het is slecht te lezen zo, ik moet echt eens LaTeX leren
...
Finally, someone let me out of my cage
Het is een vaak gemaakte (redeneer)fout om de limiet van sin x / x voor x naar 0 te willen 'bewijzen' met de regel van L'Hôpital (die trouwens gevonden is door Johann Bernoulli), zie ook hier.quote:
[..]
Ik heb er even over nagedacht, en je hebt gelijk, maar ik denk wel dat dit de manier is waarop we geacht worden dit te doen. Dan zal het wel niet volstaan als formeel bewijs, maar omdat je weet dat de regel van l'Hôpital geldt, kan je het denk ik wel gebruiken om je antwoord aannemelijk te maken. Ik zal zo even de uitwerking die ik nu heb posten, bedankt voor de hulp
Hoe je wel bewijst dat de limiet van sin x / x voor x naar 0 gelijk is aan 1 hangt af van de manier waarop je de sinusfunctie hebt gedefinieerd. Als je de sinusfunctie definieert aan de hand van de eenheidscirkel, dan ontkom je niet aan een meetkundige beschouwing om aan te tonen dat
cos x < sin x / x < 1 (0 < |x| < π/2),
waarna de insluitstelling het gewenste resultaat levert. Ik kan me trouwens moeilijk voorstellen dat ze je limieten zoals in je opgave laten bepalen zonder dat een 'standaardlimiet' als die van sin x / x voor x naar 0 bekend verondersteld wordt.
Wil je werken zonder formeel van de regel van L'Hôpital gebruik te maken dan zou je kunnen bedenken dat sin x / x gelijk is aan (sin x - sin 0)/(x - 0), zodat de limiet voor x naar 0 gelijk moet zijn aan de afgeleide functie in x = 0, i.e. cos 0 = 1.
Voor de limiet van log(1 + x)1/x = (log(1+x))/x voor x naar 0 kun je een soortgelijke redenering opzetten door dit te herschrijven als (log(1+x) - log(1))/((1+x) - 1), zodat je ziet dat de limiet hiervan voor x naar 0 gelijk moet zijn aan de afgeleide functie 1/x in x = 1 oftewel 1.
Tenslotte, om de limiet van (1 - cos x)/x2 voor x naar 0 te bepalen kun je teller en noemer van dit quotiënt met (1 + cos x) vermenigvuldigen en gebruik maken van de identiteit 1 - cos2x = sin2x, waarmee je dit quotiënt kunt herschrijven als het product (sin x / x)2∙(1/(1 + cos x)). Zo zie je direct dat de limiet voor x naar 0 gelijk moet zijn aan 12∙(1/(1+1)) = ½.
[ Bericht 0% gewijzigd door Riparius op 31-10-2011 19:20:05 ]
Dat de afgeleide van de sinus de cosinus is dat wordt meestal wel als bekend verondersteld. Dan kan je prima l'Hopital gebruiken. Maar je kan natuurlijk altijd door blijven gaan totdat je het direct uit een aantal axioma's afleidt, maar dat zal de bedoeling niet zijn.
Je zult toch iets meer context moeten geven (lees: er blijk van moeten geven dat je iets meer moeite wil doen) als je ook een antwoord verwacht. We hebben hier geen glazen bollen, maar ik vermoed dat je met gehele getallen van Gauss (Gaussian integers) bezig bent. Als dit vermoeden correct is, begin dan eens met de Nederlandse en Engelse Wikipedia artikelen over dit onderwerp door te nemen.quote:
Hallo,
voor een inleveropdracht zijn we op zoek naar een irreducibel getal waarvan de norm niet priem is. En we komen er echt niet uit. Hulp vriendelijk gevraagd
De vraag luidt: Compute .
Nu is het (in ieder geval bij de 10 omringende vragen, die ik allemaal wél snap) de bedoeling dat ik dit doe met behulp van formules betreffende (bij deze vraag finite) arithmetical en geometric series, respectievelijk
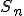=((N+1)/2)*(
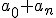) en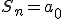 
*(1-r^(n+1))/(1-r) met r = geometrical ratio voor welke 
.
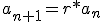Het antwoord moet zijn = 2000 + 8000 * (1-(1/1.05)^29) - 20*680/(1.05^30) = 2000 + 6056.43 - 3146.73 = 4909.70
Ik heb er een tijdje naar gekeken, maar ik snap dus niet hoe ik het moet kunnen uitrekenen en al helemaal niet hoe ik bij dat antwoord moet komen. Het probleem waar ik tegenaan loop is dat ik geen getal kan definiëren voor r, ik krijg r = ((5+n)/(4+n))/1.05. Het is echter ook niet een arithmetical sequence. Het lijkt een combinatie te zijn, maar ik snap niet hoe ik dat zou moeten uitwerken en het antwoord kan ik ook niet herleiden.
.Nu is het (in ieder geval bij de 10 omringende vragen, die ik allemaal wél snap) de bedoeling dat ik dit doe met behulp van formules betreffende (bij deze vraag finite) arithmetical en geometric series, respectievelijk
Het antwoord moet zijn = 2000 + 8000 * (1-(1/1.05)^29) - 20*680/(1.05^30) = 2000 + 6056.43 - 3146.73 = 4909.70
Ik heb er een tijdje naar gekeken, maar ik snap dus niet hoe ik het moet kunnen uitrekenen en al helemaal niet hoe ik bij dat antwoord moet komen. Het probleem waar ik tegenaan loop is dat ik geen getal kan definiëren voor r, ik krijg r = ((5+n)/(4+n))/1.05. Het is echter ook niet een arithmetical sequence. Het lijkt een combinatie te zijn, maar ik snap niet hoe ik dat zou moeten uitwerken en het antwoord kan ik ook niet herleiden.
Özil | Ki SY| Son HM| Lee SW| Taeguk Warriors|
Ik denk dat je de som beter kan omschrijven zodat ie wel geometric is.quote:
De vraag luidt: Compute [ afbeelding ].
Nu is het (in ieder geval bij de 10 omringende vragen, die ik allemaal wél snap) de bedoeling dat ik dit doe met behulp van formules betreffende (bij deze vraag finite) arithmetical en geometric series, respectievelijk
Het antwoord moet zijn [ afbeelding ] = 2000 + 8000 * (1-(1/1.05)^29) - 20*680/(1.05^30) = 2000 + 6056.43 - 3146.73 = 4909.70
Ik heb er een tijdje naar gekeken, maar ik snap dus niet hoe ik het moet kunnen uitrekenen en al helemaal niet hoe ik bij dat antwoord moet komen. Het probleem waar ik tegenaan loop is dat ik geen getal kan definiëren voor r, ik krijg r = ((5+n)/(4+n))/1.05. Het is echter ook niet een arithmetical sequence. Het lijkt een combinatie te zijn, maar ik snap niet hoe ik dat zou moeten uitwerken en het antwoord kan ik ook niet herleiden.
Waarbij de tweede som te schrijven is als
Zit voor mijn wiskunde tentamen wat sommen te maken, alles lukt zo'n beetje wel maar bij deze loop ik gewoon vast. Weet de regels niet meer met betrekking tot het delen van wortels e.d. Zou iemand deze voor mij kunnen uitwerken met uitleg?
Dus een vierde en een derde machtswortel die gedeeld worden door elkaar moet ik vereenvoudigen. V= wortelteken.
4V(9a/8b):3V(3a/4b²) = ?
Thanx alvast, antwoord moet ook in een wortel.
Volgens mij is het heel simpel, maar kom er effe niet uit.
Dus een vierde en een derde machtswortel die gedeeld worden door elkaar moet ik vereenvoudigen. V= wortelteken.
4V(9a/8b):3V(3a/4b²) = ?
Thanx alvast, antwoord moet ook in een wortel.
Volgens mij is het heel simpel, maar kom er effe niet uit.
Waarom?
Als je het als volgt opschrijft is het misschien makkelijker:quote:
Zit voor mijn wiskunde tentamen wat sommen te maken, alles lukt zo'n beetje wel maar bij deze loop ik gewoon vast. Weet de regels niet meer met betrekking tot het delen van wortels e.d. Zou iemand deze voor mij kunnen uitwerken met uitleg?
Dus een vierde en een derde machtswortel die gedeeld worden door elkaar moet ik vereenvoudigen. V= wortelteken.
4V(9a/8b):3V(3a/4b²) = ?
Thanx alvast, antwoord moet ook in een wortel.
Volgens mij is het heel simpel, maar kom er effe niet uit.
Als het dan nog niet lukt moet je het maar even zeggen
.
The biggest argument against democracy is a five minute discussion with the average voter.
quote:
http://www.artofproblemso(...)ico-geometric_series
Bedanktquote:
[..]
Ik denk dat je de som beter kan omschrijven zodat ie wel geometric is.
Waarbij de tweede som te schrijven is als
Die 1e link snapte ik niet helemaal en volgens mij wordt er (op dit moment in ieder geval) niet van mij verwacht dat ik een som op zo'n manier om kan schrijven, maar ik ben er uiteindelijk uitgekomen door deze link te gebruiken voor een som van n=0 tot 30 en dan n=0 er vanaf te trekken. Ongetwijfeld dat in die link hetzelfde staat als in die van jou, maar het staat er voor mij net iets duidelijker
Ik snap overigens nog steeds niet hoe ze bij dat antwoord komen met opeens "2000 + ...", maar goed.
Özil | Ki SY| Son HM| Lee SW| Taeguk Warriors|
Mag ik dan gewoon eerst de breuken tussen haakjes vermenigvuldigen? Nee toch?
Normaal zijn deze sommen geen probleem, maar mijn hersenen werken vandaag niet echt mee. Zou je hem verder uit kunnen werken? Met een voorbeeld lukt het bij mij altijd wel, haha.
Normaal zijn deze sommen geen probleem, maar mijn hersenen werken vandaag niet echt mee. Zou je hem verder uit kunnen werken? Met een voorbeeld lukt het bij mij altijd wel, haha.
Waarom?
Wat bedoel je precies met 'de breuken tussen haakjes vermenigvuldigen'? Maar ik zal 'm even uitwerken:
Je moet gebruikmaken van de regels
The biggest argument against democracy is a five minute discussion with the average voter.
In de herleiding in de link die je geeft staan verschillende slordigheden (minteken vergeten, haakjes vergeten, superscript vergeten voor exponenten). Maar ik neem aan dat je die ook had gespot? Als je trouwens niet begrijpt hoe men aan die 2000 komt dan kan ik alleen maar concluderen dat je het nog steeds niet hebt begrepen. Die 2000 is namelijk gewoon de eerste term ab/(1-r) in de uitdrukking voor de som zoals die in je link wordt gegeven. In jouw geval is hierbij ab = 100/1,05 en r = 1/1,05 zodat ab/(1-r) = (100/1,05)*21 = 2000.quote:
[..]
[..]
Bedankt
Die 1e link snapte ik niet helemaal en volgens mij wordt er (op dit moment in ieder geval) niet van mij verwacht dat ik een som op zo'n manier om kan schrijven, maar ik ben er uiteindelijk uitgekomen door deze link te gebruiken voor een som van n=0 tot 30 en dan n=0 er vanaf te trekken. Ongetwijfeld dat in die link hetzelfde staat als in die van jou, maar het staat er voor mij net iets duidelijker
Ik snap overigens nog steeds niet hoe ze bij dat antwoord komen met opeens "2000 + ...", maar goed.
Ah, zo had ik het ook gedaan. Maar bij de antwoorden stond 9/2ab^5 in plaats van de 9b^5/2a waar jij en ik op uit kwamen.quote:
Wat bedoel je precies met 'de breuken tussen haakjes vermenigvuldigen'? Maar ik zal 'm even uitwerken:
Je moet gebruikmaken van de regelsen
. Als je dat doet krijg je
Bedankt in ieder geval.
Waarom?
Daar ben ik weer
Bereken:
(2+i)(3+i)
Antwoord lijkt me simpel en is 5+5i
volgende vraag lijkt erop:
(5+i)(2+3i)
Echter staat er hier boven de (5+i) een lijn. Ik kan niet eens vinden hoe ik dit met de texifier doe, maar gewoon een horizontale lijn boven het gehele gedeelte (5+i). Wat betekent dit en waarom is dit anders dan gewoon (5+i)(2+3i)?
Bereken:
(2+i)(3+i)
Antwoord lijkt me simpel en is 5+5i
volgende vraag lijkt erop:
(5+i)(2+3i)
Echter staat er hier boven de (5+i) een lijn. Ik kan niet eens vinden hoe ik dit met de texifier doe, maar gewoon een horizontale lijn boven het gehele gedeelte (5+i). Wat betekent dit en waarom is dit anders dan gewoon (5+i)(2+3i)?
Ze keek me smerig aan ik vond 'm zelf nog zo subtiel
maar ze kon ze niet waarderen, grappen over Tsjernobyl
maar ze kon ze niet waarderen, grappen over Tsjernobyl
Die lijn staat voor complexe conjugatie.quote:
Daar ben ik weer
Bereken:
(2+i)(3+i)
Antwoord lijkt me simpel en is 5+5i
volgende vraag lijkt erop:
(5+i)(2+3i)
Echter staat er hier boven de (5+i) een lijn. Ik kan niet eens vinden hoe ik dit met de texifier doe, maar gewoon een horizontale lijn boven het gehele gedeelte (5+i). Wat betekent dit en waarom is dit anders dan gewoon (5+i)(2+3i)?
Is het complex geconjugeerde van (5+i) dan (5-i). En zo ja: wat is precies de functie/het nut daarvan?quote:
[..]
Die lijn staat voor complexe conjugatie.
Ze keek me smerig aan ik vond 'm zelf nog zo subtiel
maar ze kon ze niet waarderen, grappen over Tsjernobyl
maar ze kon ze niet waarderen, grappen over Tsjernobyl
Bedenk dat zowel som als product van twee geconjugeerde complexe getallen reëel zijn. Dat heeft bijvoorbeeld als consequentie dat complexe nulpunten van polynomen met reële coëfficiënten altijd in geconjugeerde paren optreden. Kijk verder even hier.quote:
[..]
Is het complex geconjugeerde van (5+i) dan (5-i). En zo ja: wat is precies de functie/het nut daarvan?
Bedankt. Vind het toch wel een lastig stuk, dus ga me er straks nog even verder in verdiepen. Puur rekentechnisch klopt het wel dat:quote:
[..]
Bedenk dat zowel som als product van twee geconjugeerde complexe getallen reëel zijn. Dat heeft bijvoorbeeld als consequentie dat complexe nulpunten van polynomen met reële coëfficiënten altijd in geconjugeerde paren optreden. Kijk verder even hier.
(5+i)(2+3i) = 13 + 13i
(waarbij (5+i) dus geconjugeerd moet worden)
?
Ze keek me smerig aan ik vond 'm zelf nog zo subtiel
maar ze kon ze niet waarderen, grappen over Tsjernobyl
maar ze kon ze niet waarderen, grappen over Tsjernobyl
Ja, hoewel je dat zo niet op moet schrijven, dat is te verwarrend. Je hebt:quote:
[..]
Bedankt. Vind het toch wel een lastig stuk, dus ga me er straks nog even verder in verdiepen. Puur rekentechnisch klopt het wel dat:
(5+i)(2+3i) = 13 + 13i
(waarbij (5+i) dus geconjugeerd moet worden)
?
(5 + i)(2 + 3i) = 7 + 17i
(5 - i)(2 + 3i) = 13 + 13i
De som van deze producten moet uiteraard 10(2 + 3i) = 20 + 30i zijn, en dat klopt.
Mijn manier komt ook goed uit . Op zich lijkt me mijn methode makkelijker dan nog zo'n formule uit je hoofd leren.quote:
[..]
[..]
Bedankt
Die 1e link snapte ik niet helemaal en volgens mij wordt er (op dit moment in ieder geval) niet van mij verwacht dat ik een som op zo'n manier om kan schrijven, maar ik ben er uiteindelijk uitgekomen door deze link te gebruiken voor een som van n=0 tot 30 en dan n=0 er vanaf te trekken. Ongetwijfeld dat in die link hetzelfde staat als in die van jou, maar het staat er voor mij net iets duidelijker
Ik snap overigens nog steeds niet hoe ze bij dat antwoord komen met opeens "2000 + ...", maar goed.
Het idee is vrij simpel, schrijf het maar eens uit voor een paar termen. Je brengt het terug naar een som van de vorm
Je krijgt dus 1*r^2 + 2*r^2 + 3*r^3 + ... + N r^N. Als je die n weglaat dan krijg je een standaard meetkundige reeks die je kan berekenen:
Echter, je mist nog een hoop termen, namelijk:
Dan bereken je
Ik begrijp hem. Bedankt manquote:
[..]
Ja, hoewel je dat zo niet op moet schrijven, dat is te verwarrend. Je hebt:
(5 + i)(2 + 3i) = 7 + 17i
(5 - i)(2 + 3i) = 13 + 13i
De som van deze producten moet uiteraard 10(2 + 3i) = 20 + 30i zijn, en dat klopt.
Ze keek me smerig aan ik vond 'm zelf nog zo subtiel
maar ze kon ze niet waarderen, grappen over Tsjernobyl
maar ze kon ze niet waarderen, grappen over Tsjernobyl
Je zou ook kunnen bedenken dat:quote:
[..]
Mijn manier komt ook goed uit . Op zich lijkt me mijn methode makkelijker dan nog zo'n formule uit je hoofd leren.
Het idee is vrij simpel, schrijf het maar eens uit voor een paar termen. Je brengt het terug naar een som van de vorm
De tweede som in het rechterlid is een meetkundige reeks, en dus eenvoudig uit te drukken in r en N. De termen van de gedaante (n+1)rn in de eerste som in het rechterlid kun je opvatten als de afgeleide van rn+1 naar r, zodat je deze som ook eenvoudig kunt bepalen door eerst de meetkundige reeks met termen van de gedaante rn+1 voor n = 1 .. N te sommeren en de resulterende uitdrukking in r en N te differentiëren naar r.
Dat is misschien nog wel de elegantste manierquote:
[..]
Je zou ook kunnen bedenken dat:
De tweede som in het rechterlid is een meetkundige reeks, en dus eenvoudig uit te drukken in r en N. De termen van de gedaante (n+1)rn in de eerste som in het rechterlid kun je opvatten als de afgeleide van rn+1 naar r, zodat je deze som ook eenvoudig kunt bepalen door eerst de meetkundige reeks met termen van de gedaante rn+1 voor n = 1 .. N te sommeren en de resulterende uitdrukking in r en N te differentiëren naar r.
Sorry dat ik weer over complexe getallen begin, maar ik begrijp het nu al niet meer
(3 - 2i)2i
Het leek mij vrij simpel door zo te berekenen:
9 - 4i2 = 9 + 4 = 13
= 13i
Maar volgens wolframalpha is het antwoord:
12 + 5i
Kan iemand me uitleggen waarom wolframalpha gelijk heeft en wat ik fout doe?
(3 - 2i)2i
Het leek mij vrij simpel door zo te berekenen:
9 - 4i2 = 9 + 4 = 13
= 13i
Maar volgens wolframalpha is het antwoord:
12 + 5i
Kan iemand me uitleggen waarom wolframalpha gelijk heeft en wat ik fout doe?
Ze keek me smerig aan ik vond 'm zelf nog zo subtiel
maar ze kon ze niet waarderen, grappen over Tsjernobyl
maar ze kon ze niet waarderen, grappen over Tsjernobyl
Weet je wat een merkwaardig product is? Dus, bijvoorbeeld:quote:
Sorry dat ik weer over complexe getallen begin, maar ik begrijp het nu al niet meer
(3 - 2i)2i
Het leek mij vrij simpel door zo te berekenen:
9 - 4i2 = 9 + 4 = 13
= 13i
Maar volgens wolframalpha is het antwoord:
12 + 5i
Kan iemand me uitleggen waarom wolframalpha gelijk heeft en wat ik fout doe?
(a + b)2 = a2 + 2ab + b2
Komt je dit niet bekend voor, lees dan even dit.
Pff, ik schaam me een beetjequote:
[..]
Weet je wat een merkwaardig product is? Dus, bijvoorbeeld:
(a + b)2 = a2 + 2ab + b2
Komt je dit niet bekend voor, lees dan even dit.
Hiermee is het natuurlijk meteen duidelijk. Heel erg bedankt
Ze keek me smerig aan ik vond 'm zelf nog zo subtiel
maar ze kon ze niet waarderen, grappen over Tsjernobyl
maar ze kon ze niet waarderen, grappen over Tsjernobyl
Beschouw F(x)=f(x)g(x)
"Guess a formula for F^(n)" De n-de afgeleide van F(x)=f(x)g(x)
De expansie lijkt identiek aan de driehoek van pascal, maar ik weet niet precies hoe ik dit nou formuleren...
Met tot de macht bedoel ik de n-de afgeleide.
F^(n)=f^(n)g+nf^(n-1)g^1.....+nf^1g^(n-1)+fg^(n)
Is wat ik zie..
"Guess a formula for F^(n)" De n-de afgeleide van F(x)=f(x)g(x)
De expansie lijkt identiek aan de driehoek van pascal, maar ik weet niet precies hoe ik dit nou formuleren...
Met tot de macht bedoel ik de n-de afgeleide.
F^(n)=f^(n)g+nf^(n-1)g^1.....+nf^1g^(n-1)+fg^(n)
Is wat ik zie..
De gangbare notatie voor de n-de afgeleide van F(x) voor n > 3 is F(n)(x), het is immers niet de bedoeling dit met een macht te verwarren. Sommige auteurs gebruiken ook Romeinse cijfers in onderkast, met of zonder haakjes, dus e.g. fiv voor de vierde afgeleide van f.quote:
Beschouw F(x)=f(x)g(x)
"Guess a formula for F^(n)" De n-de afgeleide van F(x)=f(x)g(x)
Je bedoelt dat je binomiaalcoëfficiënten ziet verschijnen in je expansie.quote:De expansie lijkt identiek aan de driehoek van Pascal, maar ik weet niet precies hoe ik dit nou moet formuleren ...
Zo dus:quote:Met tot de macht bedoel ik de n-de afgeleide.
F^(n)=f^(n)g+nf^(n-1)g^1.....+nf^1g^(n-1)+fg^(n)
Is wat ik zie..
Dit heet wel de regel van Leibniz.
Kan iemand mij een stappenplan geven hoe je implicit differentiation toepast? Bijvoorbeeld bij deze opgave:
Find the slope of the tangent to the graph in point (2,1) for: y³ + 3x²y = 13
Ans: y-1 = (- 4/5)(x-2)
Snap er vrij weinig van
edit:
Leraar doet 't telkens zo:
3y(x)²y(x)² etc.
Maar het boek laat die (x) gewoon weg (wat 't er al iets logischer uit laat zien) .. waarom add hij hier die (x) en is het een schande als dit weg blijft?
Edit 2: zo doet de leraar het:
Edit 3: en het boek maakt er dit van:
3y²y' + 6xy + 3x²y' = 0
y' = -6xy / 3x²+3y² = -2xy/x²+y²
for x = 2 and y = 1 we find y' = -4/5
[ Bericht 21% gewijzigd door Sokz op 02-11-2011 17:11:10 ]
Find the slope of the tangent to the graph in point (2,1) for: y³ + 3x²y = 13
Ans: y-1 = (- 4/5)(x-2)
Snap er vrij weinig van
edit:
Leraar doet 't telkens zo:
3y(x)²y(x)² etc.
Maar het boek laat die (x) gewoon weg (wat 't er al iets logischer uit laat zien) .. waarom add hij hier die (x) en is het een schande als dit weg blijft?
Edit 2: zo doet de leraar het:
Edit 3: en het boek maakt er dit van:
3y²y' + 6xy + 3x²y' = 0
y' = -6xy / 3x²+3y² = -2xy/x²+y²
for x = 2 and y = 1 we find y' = -4/5
[ Bericht 21% gewijzigd door Sokz op 02-11-2011 17:11:10 ]
Het antwoord dat je erbij post is niet het antwoord op de gestelde vraag. Bij impliciet differentiëren beschouw je y als functie van x (of x als functie van y) en pas je de gebruikelijke regels voor het differentiëren toe. In dit geval kun je y als functie van x beschouwen en ben je geïnteresseerd in de waarde van y' voor x = 2 en y = 1.quote:Op woensdag 2 november 2011 17:01 schreef Sokz het volgende:
Kan iemand mij een stappenplan geven hoe je implicit differentiation toepast? Bijvoorbeeld bij deze opgave:
Find the slope of the tangent to the graph in point (2,1) for: y³ + 3x²y = 13
Ans: y-1 = (- 4/5)(x-2)
Snap er vrij weinig van
Het is toch juist mooi om y(x) op te schrijven? Dan laat je gelijk zien dat y een functie is van x.quote:
Maar het boek laat die (x) gewoon weg (wat 't er al iets logischer uit laat zien) .. waarom add hij hier die (x) en is het een schande als dit weg blijft?
Ja maar voor mijn hersenen is dat andere wat rustiger.quote:
[..]
Het is toch juist mooi om y(x) op te schrijven? Dan laat je gelijk zien dat y een functie is van x.
Maargoed het is dus enkel voor de 'mooiigheid?'
Lijkt mij wel.quote:
[..]
Ja maar voor mijn hersenen is dat andere wat rustiger.
Je laat impliciet al zien dat y een functie is van x door y^3 + 3x^(2) * y gelijk te stellen aan een constante.
De leraar voert een andere opdracht uit dan de vraagstelling en gebruikt een niet heel overzichtelijke notatie. Hij/zij stelt de vergelijking van de raaklijn aan de curve in het punt (2;1) op, en dat was niet de vraag, want gevraagd wordt alleen de slope (richtingscoëfficiënt) van de raaklijn, niet de vergelijking.quote:
Kan iemand mij een stappenplan geven hoe je implicit differentiation toepast? Bijvoorbeeld bij deze opgave:
Find the slope of the tangent to the graph in point (2,1) for: y³ + 3x²y = 13
Ans: y-1 = (- 4/5)(x-2)
Snap er vrij weinig van
edit:
Leraar doet 't telkens zo:
3y(x)²y(x)² etc.
Maar het boek laat die (x) gewoon weg (wat 't er al iets logischer uit laat zien) .. waarom add hij hier die (x) en is het een schande als dit weg blijft?
Edit 2: zo doet de leraar het:
[ afbeelding ]
Edit 3: en het boek maakt er dit van:
3y²y' + 6xy + 3x²y' = 0
y' = -6xy / 3x²+3y² = -2xy/x²+y²
for x = 2 and y = 1 we find y' = -4/5
Het boek doet het goed maar niet op de meest eenvoudige manier, want je kunt na het impliciet differentiëren meteen x = 2 en y = 1 invullen zodat je een lineaire vergelijking in y' overhoudt.
[ Bericht 0% gewijzigd door Riparius op 02-11-2011 19:01:28 ]
Lekkere leraar heb ik dan. Maar bedankt hier kan ik zeker weer mee vooruit !
Edit: Toch nog een vraagje .. hoe komt men aan die - 6xy? Waarom is die negatief?
edit2: Nevermind ik zie 't al .. ze slaan 't stapje 6xy naar de andere kant halen over.
[ Bericht 18% gewijzigd door Sokz op 02-11-2011 17:31:55 ]
Maar bedankt hier kan ik zeker weer mee vooruit !Edit: Toch nog een vraagje .. hoe komt men aan die - 6xy? Waarom is die negatief?
edit2: Nevermind ik zie 't al .. ze slaan 't stapje 6xy naar de andere kant halen over.
[ Bericht 18% gewijzigd door Sokz op 02-11-2011 17:31:55 ]
Ik zou het als volgt doen. De vergelijking van de curve is:quote:
Lekkere leraar heb ik dan.
(1) y3 + 3x2y = 13
Impliciet differentiëren naar x geeft:
(2) 3y2y' + 6xy + 3x2y' = 0
Substitutie van x = 2 en y = 1 geeft:
(3) 3y' + 12 + 12y' = 0
En dus krijgen we:
(4) y' = -12/15 = -4/5.
Eenvoudig toch?
