SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Amen... ik blijf dit soort dingen lastig vinden... practice makes perfect I guess.quote:Op donderdag 15 september 2011 16:03 schreef Haushofer het volgende:
Substitutie: noem u = -\lambda(x-a)^2, dan du -2\lambda(x-a) dx.
Dit kun je altijd doen als de macht van x in de exponent 1 hoger is dan de macht van x in de integraal
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.
Weet iemand toevallig hoe ik deze recursieve definitie om kan schrijven naar een directe formule? Het is een beetje weggezakt, en een huisgenoot doet een één of ander bedrijfskundevak waar 't relevant is. Met een recursief programma kan ik 't nog wel oplossen bij n = 40, maar met het handje op 't tentamen is 't nogal wat werk..
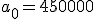
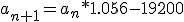
Dit is de opgave toch?quote:Op donderdag 15 september 2011 17:48 schreef Sokz het volgende:
volgende som (sqrt in een sqrt) staat gelijk aan C.
1....
1+R - A ............ = C
1....
1+R + B
Hoe krijg ik R hieruit? (let niet op de puntjes)
wat heb ik tot dusverre geprobeert:
A/B = C » A = C
A/B - C = 0 en dan verder uitwerken (kom ik ook niet verder)
A/B * B = C*B » A = CB kump ik ook niet verder
Eerst vermenigvuldigen we dan de teller en de noemer met 1+R:
Dan vermenigvuldigen we links en rechts met 1+B+BR:
Dan halen we de termen met R naar een kant:
Dan halen we R buiten haakjes:
En dan delen we door BC+A
The biggest argument against democracy is a five minute discussion with the average voter.
Hee jongens, ik heb weer een vraag 
Kan iemand mij helpen met dit?
Bepaal de inverse functie van
N = f(L) = 1
Hoe zoek ik dan uit wat L is?
Kan iemand mij helpen met dit?
Bepaal de inverse functie van
N = f(L) = 1
Hoe zoek ik dan uit wat L is?
In het algemeen:quote:
Weet iemand toevallig hoe ik deze recursieve definitie om kan schrijven naar een directe formule? Het is een beetje weggezakt, en een huisgenoot doet een één of ander bedrijfskundevak waar 't relevant is. Met een recursief programma kan ik 't nog wel oplossen bij n = 40, maar met het handje op 't tentamen is 't nogal wat werk..
Stel a0 = b en an+1 = c an + d.
Dan krijg je dus
a1 = c a0 + d = cb + d
a2 = c a1 + d = c(cb+d) + d = c²b + cd + d
a3 = c a2 + d = c(c(cb+d)+d) + d = c³b + c² d + cd + d
Aan het patroon zie je dat je dan krijgt
an = cn b + cn-1 d + ... + c1d + d
Wat is f, wat is L, wat is N?quote:Op donderdag 15 september 2011 19:31 schreef Snuf. het volgende:
Hee jongens, ik heb weer een vraag
Kan iemand mij helpen met dit?
Bepaal de inverse functie van
N = f(L) = 1
Hoe zoek ik dan uit wat L is?
quote:
[..]
Dit is de opgave toch?
Eerst vermenigvuldigen we dan de teller en de noemer met 1+R:
Dan vermenigvuldigen we links en rechts met 1+B+BR:
Dan halen we de termen met R naar een kant:
Dan halen we R buiten haakjes:
En dan delen we door BC+A
Daar was ik me van bewust (met een sigmanotatie is het nog best overzichtelijk) maar dat lost het probleem nog niet op: n = 40 zonder grafische rekenmachine / computerquote:
[..]
In het algemeen:
Stel a0 = b en an+1 = c an + d.
Dan krijg je dus
a1 = c a0 + d = cb + d
a2 = c a1 + d = c(cb+d) + d = c²b + cd + d
a3 = c a2 + d = c(c(cb+d)+d) + d = c³b + c² d + cd + d
Aan het patroon zie je dat je dan krijgt
an = cn b + cn-1 d + ... + c1d + d
Jawel, want je kunt de som van een meetkundige reeks makkelijk berekenen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Aangenomen dat je logaritmen met grondtal 10 bedoelt, is dat dus gewoon een macht van 10 ...quote:
Hoe bereken je de inverse logaritme van -2,5 ? (scheikunde, iets met pH en concentratie)
Ik zie 't nog niet helemaal geloof ikquote:
Jawel, want je kunt de som van een meetkundige reeks makkelijk berekenen.
Welk positief reëel getal niet?quote:
[..]
Aangenomen dat je logaritmen met grondtal 10 bedoelt, is dat dus gewoon een macht van 10 ...
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Je kunt an = cn b + cn-1 d + ... + c1d + d schrijven als:quote:
[..]
Ik zie 't nog niet helemaal geloof ik
an = cn b + (cn-1 + ... + c1 + c0)d
= cn b + (cn - c0) / (c-1) * d
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
72 -(4+x)2 - (4-rx)2
Ik wil deze omzetten naar de quadratic function.
Dus ax +bx2 + c
Ik begin zo:
72 - [ (4+x)(4+x) ] - [ (4-rx)(4+rx) ]
72 - (16+4x+4x+x2) - (16 + 4rx - 4rx +r2x2)
72 - 16 - 8x - x2 - 16 - 4rx + 4rx + r2x2
40 - 8x - x2 + r2x2
Dit gaat volgens mij niet helemaal goed want ik mis 8rx..
Iemand weet waar ik foutje maak? En hoe ik het beste verder kan gaan om in die vorm te krijgen?
Ik wil deze omzetten naar de quadratic function.
Dus ax +bx2 + c
Ik begin zo:
72 - [ (4+x)(4+x) ] - [ (4-rx)(4+rx) ]
72 - (16+4x+4x+x2) - (16 + 4rx - 4rx +r2x2)
72 - 16 - 8x - x2 - 16 - 4rx + 4rx + r2x2
40 - 8x - x2 + r2x2
Dit gaat volgens mij niet helemaal goed want ik mis 8rx..
Iemand weet waar ik foutje maak? En hoe ik het beste verder kan gaan om in die vorm te krijgen?
Je schrijft (4-rx)2 verkeerd uit, dus de eerste regel gaat al fout. Verder doe je het wel goed.quote:
72 -(4+x)2 - (4-rx)2
Ik wil deze omzetten naar de quadratic function.
Dus ax +bx2 + c
Ik begin zo:
72 - [ (4+x)(4+x) ] - [ (4-rx)(4+rx) ]
72 - (16+4x+4x+x2) - (16 + 4rx - 4rx +r2x2)
72 - 16 - 8x - x2 - 16 - 4rx + 4rx + r2x2
40 - 8x - x2 + r2x2
Dit gaat volgens mij niet helemaal goed want ik mis 8rx..
Iemand weet waar ik foutje maak? En hoe ik het beste verder kan gaan om in die vorm te krijgen?
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!
Een aardige site is b.v. SOS Math Calculus, en voor jou dan het kopje "TECHNIQUES OF INTEGRATION". Staan de meeste truukjes en handigheidjes wel opquote:
[..]
Amen... ik blijf dit soort dingen lastig vinden... practice makes perfect I guess.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
72 - [ (4+x)(4+x) ] - [ (4-rx)(4-rx) ]
72 - (16+4x+4x+x2) - (16 - 4rx - 4rx - r2x2)
72 - 16 - 8x - x2 - 16 + 4rx + 4rx - r2x2
40 - 8x + 8rx - x2 - r2x2
-(r2 -1)x2 + 8(r-1)x - 40
Dus a = (r2 -1)
en b = 8(r-1)
maar dan klopt ie niet dus wordt het dit toch?:
-(r2 -1)x2 + 8(r-1)x2 + 40
72 - (16+4x+4x+x2) - (16 - 4rx - 4rx - r2x2)
72 - 16 - 8x - x2 - 16 + 4rx + 4rx - r2x2
40 - 8x + 8rx - x2 - r2x2
-(r2 -1)x2 + 8(r-1)x - 40
Dus a = (r2 -1)
en b = 8(r-1)
maar dan klopt ie niet dus wordt het dit toch?:
-(r2 -1)x2 + 8(r-1)x2 + 40
Betekent "dan en slechts dan als" hetzelfde als "precies dan als"?
Bij "Bewijs dat A dan en slechts dan als B" moet je de bewering van beide kanten aantonen. Moet dat ook bij "Bewijs dat A precies dan als B"?
Het lijkt me van wel maar ik wil het graag zeker weten voordat ik het verkeerd doe.
Bij "Bewijs dat A dan en slechts dan als B" moet je de bewering van beide kanten aantonen. Moet dat ook bij "Bewijs dat A precies dan als B"?
Het lijkt me van wel maar ik wil het graag zeker weten voordat ik het verkeerd doe.
Nee. Hier maak je een tekenfout. Leer trouwens je merkwaardige producten.quote:
72 - [ (4+x)(4+x) ] - [ (4-rx)(4-rx) ]
72 - (16+4x+4x+x2) - (16 - 4rx - 4rx - r2x2)
72 - 16 - 8x - x2 - 16 + 4rx + 4rx - r2x2
Ja, maar de formulering die je hier zelf gebruikt is niet gangbaar.quote:
Betekent "dan en slechts dan als" hetzelfde als "precies dan als"?
Nee, dat moet je niet. Als uit de geldigheid van B volgt dat A geldt mag je dat niet omkeren en zeggen dat uit de geldigheid van A volgt dat B geldt. Wat je wel moet laten zien is dat als niet B, dan ook niet A.quote:Bij "Bewijs dat A dan en slechts dan als B" moet je de bewering van beide kanten aantonen.
thanks again, nu is ie correct denk ik.quote:
[..]
Nee. Hier maak je een tekenfout. Leer trouwens je merkwaardige producten.
72 - 16 - 8x - x2 - 16 + 4rx + 4rx + r2x2
- 8x - x2 + 8rx + r2x2 + 40
(r2-1)x2 - 8(r-1)x + 40
Nee, nog niet. Weer een tekenfout.quote:
[..]
thanks again, nu is ie correct denk ik.
72 - 16 - 8x - x2 - 16 + 4rx + 4rx + r2x2
- 8x - x2 + 8rx + r2x2 + 40
(r2-1)x2 - 8(r-1)x + 40
Ik heb me altijd al afgevraagd waar de constructie "dan en slechts dan als" zo vaak gebruikt wordt. Is "alleen als" niet voldoende?
Als je zegt "A alleen als B", dan betekent dat volgens mij ook gewoon dat [als B dan A] en [als niet B dan niet A]... precies hetzelfde als "A dan en slechts dan als B" toch? Alleen een stuk minder woorden.
Als je zegt "A alleen als B", dan betekent dat volgens mij ook gewoon dat [als B dan A] en [als niet B dan niet A]... precies hetzelfde als "A dan en slechts dan als B" toch? Alleen een stuk minder woorden.
Met ''A alleen als B'' zeg je alleen dat A uit B volgt en dat niet per se ook geldt dat B uit A volgt.quote:
Ik heb me altijd al afgevraagd waar de constructie "dan en slechts dan als" zo vaak gebruikt wordt. Is "alleen als" niet voldoende?
Als je zegt "A alleen als B", dan betekent dat volgens mij ook gewoon dat [als B dan A] en [als niet B dan niet A]... precies hetzelfde als "A dan en slechts dan als B" toch? Alleen een stuk minder woorden.
Dit is echter juist wat ''dan en slechts dan als'' aangeeft, dit betekent dat er een equivalentie is, dus dat zowel A uit B volgt als B uit A volgt.
http://nl.wikipedia.org/wiki/Dan_en_slechts_dan_als
Een voorbeeld van ''als A dan B'' is bijvoorbeeld dat als 2 variabelen onafhankelijk zijn geldt dat hun covariantie 0 is.
Echter, als de covariantie van 2 variabelen 0 is betekent dit niet automatisch dat ze onafhankelijk zijn.
Beneath the gold, bitter steel
Zou iemand mij de solution of a system of linear equations uitleggen? Ik snap het verschil niet tussen one solution, infinetely many solutions of no solutions
Een lineaire vergelijking (we nemen even twee variabelen) kan je zien als een lijn in R2. De oplossing van een stelsel lineaire vergelijkingen is nu het punt, of de punten, waar de verschillende lijnen elkaar snijden. Als de lijnen evenwijdig lopen (maar niet overlappen) is er geen enkel punt waar ze snijden, dus is er geen oplossing. Als ze niet evenwijdig lopen is er precies één punt waar ze snijden en als ze overlappen dan zijn er oneindig veel oplossingen (alle punten op de lijn).quote:
Zou iemand mij de solution of a system of linear equations uitleggen? Ik snap het verschil niet tussen one solution, infinetely many solutions of no solutions
The biggest argument against democracy is a five minute discussion with the average voter.
Aha bedankt, het begint me inderdaad al weer wat te dagen.
Zou iemand het nog wat kunnen uitbreiden met dit voorbeeld?
Bepaal a en b in deze lineare vergelijking zo dat je deze resultaten A. infinitely many solutions, B. No solutions en C. Precisely one solution. krijgt?
ax1 + x2 = 2
2x1 + 2x2 =b
Alvast hartstikke bedankt!
Zou iemand het nog wat kunnen uitbreiden met dit voorbeeld?
Bepaal a en b in deze lineare vergelijking zo dat je deze resultaten A. infinitely many solutions, B. No solutions en C. Precisely one solution. krijgt?
ax1 + x2 = 2
2x1 + 2x2 =b
Alvast hartstikke bedankt!
Met het plaatje in mijn vorige post moet dat toch wel te doen zijn? Probeer het eerst zelf op te lossen!quote:
Aha bedankt, het begint me inderdaad al weer wat te dagen.
Zou iemand het nog wat kunnen uitbreiden met dit voorbeeld?
Bepaal a en b in deze lineare vergelijking zo dat je deze resultaten A. infinitely many solutions, B. No solutions en C. Precisely one solution. krijgt?
ax1 + x2 = 2
2x1 + 2x2 =b
Alvast hartstikke bedankt!
The biggest argument against democracy is a five minute discussion with the average voter.
Kies gewoon a en b zodanig dat 2 lijnen elkaar snijden, parallel liggen en over elkaar liggen.quote:
Aha bedankt, het begint me inderdaad al weer wat te dagen.
Zou iemand het nog wat kunnen uitbreiden met dit voorbeeld?
Bepaal a en b in deze lineare vergelijking zo dat je deze resultaten A. infinitely many solutions, B. No solutions en C. Precisely one solution. krijgt?
ax1 + x2 = 2
2x1 + 2x2 =b
Alvast hartstikke bedankt!
Dat moet je toch wel kunnen, standaard middelbare school werk.
Beneath the gold, bitter steel
Je kunt ook zo zonder rekenwerk al zien dat de lijnen parallel zullen lopen indien a = 1 (zie je ook waarom?). Dan kunnen ze nog evenwijdig zijn of samenvallen, afhankelijk van de waarde van b. Voor b = 4 vallen ze dan samen, en is b ongelijk aan 4 dan lopen ze evenwijdig. Is a evenwel ongelijk aan 1, dan zullen de lijnen elkaar snijden, ongeacht de waarde van b.quote:
Aha bedankt, het begint me inderdaad al weer wat te dagen.
Zou iemand het nog wat kunnen uitbreiden met dit voorbeeld?
Bepaal a en b in deze lineare vergelijking zo dat je deze resultaten A. infinitely many solutions, B. No solutions en C. Precisely one solution. krijgt?
ax1 + x2 = 2
2x1 + 2x2 =b
Alvast hartstikke bedankt!
Het is geen huiswerk maar ik wil het wat beter begrijpen.
Je kan een decimaal getal omzetten naar een binair getal door te kijken wat de grootste factor van 2 is die hierin voorkomt, die ervan af te trekken, te kijken wat de grootste factor van 2 is die in het restant overblijft, die ervan af te trekken enz.
Bijv. bij het getal 69 kan je 64 ervan aftrekken, van die 5 kan je 4 aftrekken en dan houd je 1 over. Om 64 te schrijven moet je op de zevende positie van rechts een 1 schrijven (2^7), om 4 te schrijven moet je op de 3de positie van rechts een 1 schrijven en om 1 te schrijven moet je op de 1ste positie van rechts een 1 schrijven: 1000101.
Deze methode vergt m.i. weinig inzicht, je moet slechts weten wat de machten van 2 zijn.
Er is nog een andere populaire methode die ik nog niet kende: steeds delen door twee, het restant opschrijven en vervolgens die restanten van onder naar boven van links naar rechts noteren.
Bijv.
Binaire notatie van 13: 1101
Het uitvoeren van dit algoritme is geen probleem, in grote lijnen begrijp ik de truuc ook wel: doordat je in het binaire stelsel steeds met een vermenigvuldiging van 2 werkt (1, 2 , 4, 8, 16) werkt het delen door twee. Bij gemakkelijke getallen (1, 2, 4, 8, 16, 32 enz.) zie ik ook nog wel hoe de truuc werkt. Ik mis nog het inzicht om in te zien hoe het komt dat deze truuc ook bij andere getallen werkt zoals bij het bovenstaande voorbeeld van 13.
Je kan een decimaal getal omzetten naar een binair getal door te kijken wat de grootste factor van 2 is die hierin voorkomt, die ervan af te trekken, te kijken wat de grootste factor van 2 is die in het restant overblijft, die ervan af te trekken enz.
Bijv. bij het getal 69 kan je 64 ervan aftrekken, van die 5 kan je 4 aftrekken en dan houd je 1 over. Om 64 te schrijven moet je op de zevende positie van rechts een 1 schrijven (2^7), om 4 te schrijven moet je op de 3de positie van rechts een 1 schrijven en om 1 te schrijven moet je op de 1ste positie van rechts een 1 schrijven: 1000101.
Deze methode vergt m.i. weinig inzicht, je moet slechts weten wat de machten van 2 zijn.
Er is nog een andere populaire methode die ik nog niet kende: steeds delen door twee, het restant opschrijven en vervolgens die restanten van onder naar boven van links naar rechts noteren.
Bijv.
| 1 2 3 4 5 | 13 6 1 3 0 1 1 0 1 |
Binaire notatie van 13: 1101
Het uitvoeren van dit algoritme is geen probleem, in grote lijnen begrijp ik de truuc ook wel: doordat je in het binaire stelsel steeds met een vermenigvuldiging van 2 werkt (1, 2 , 4, 8, 16) werkt het delen door twee. Bij gemakkelijke getallen (1, 2, 4, 8, 16, 32 enz.) zie ik ook nog wel hoe de truuc werkt. Ik mis nog het inzicht om in te zien hoe het komt dat deze truuc ook bij andere getallen werkt zoals bij het bovenstaande voorbeeld van 13.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Ik weet wel wat d.e.s.d.a. betekent, en ik gebruik het zelf ook zo omdat het me zo is aangeleerd, maar alsnog snap ik niet waarom "slechts als" of "alleen als" niet genoeg is.quote:
[..]
Met ''A alleen als B'' zeg je alleen dat A uit B volgt en dat niet per se ook geldt dat B uit A volgt.
Dit is echter juist wat ''dan en slechts dan als'' aangeeft, dit betekent dat er een equivalentie is, dus dat zowel A uit B volgt als B uit A volgt.
http://nl.wikipedia.org/wiki/Dan_en_slechts_dan_als
Een voorbeeld van ''als A dan B'' is bijvoorbeeld dat als 2 variabelen onafhankelijk zijn geldt dat hun covariantie 0 is.
Echter, als de covariantie van 2 variabelen 0 is betekent dit niet automatisch dat ze onafhankelijk zijn.
Jij zegt dat "A alleen als B" alleen betekent dat B impliceert A (wat trouwens fout is volgens de link in de edit, precies andersom), maar dan had ik net zo goed het woordje "alleen" weg kunnen laten. Dan krijg je "A als B". Volgens jou is "A alleen als B" en "A als B" dus hetzelfde, en dat vind ik raar. Het woordje "alleen" erbij geeft in mijn ogen aan dat het in andere gevallen niet zo is. Dus als B niet geldt, dan geldt A ook niet. En dat is equivalent met "A impliceert B". Dus dan zijn A en B equivalent. Wat klopt er niet aan deze redenering?
edit:
Nog steeds vind ik het niet echt logisch. Ik heb even een discussie hierover gevonden in het Engels.
http://forums.philosophyf(...)d-only-if-27842.html
Daar wordt als voorbeeld gegeven dat "Ik slaag alleen als ik meer dan 50 punten heb" nog steeds kan betekenen dat je met 51 punten zakt. Dat vind ik een beetje raar klinken.
Het zit hem in het feit dat ik "alleen als" zie als een sterkere uitspraak dan "als". Dus "alleen als" impliceert "als". Blijkbaar vindt men dat dat niet zo is
... puur een kwestie van conventie/taalinterpretatie denk ik.[ Bericht 1% gewijzigd door thenxero op 17-09-2011 18:55:29 ]
Ja het zal inderdaad met conventie te maken hebben, want als je ''alleen als' gebruikt voor een equivalentie, hoe zou je dan een eenzijdige implicatie simpel en duidelijk willen formuleren?quote:
[..]
Ik weet wel wat d.e.s.d.a. betekent, en ik gebruik het zelf ook zo omdat het me zo is aangeleerd, maar alsnog snap ik niet waarom "slechts als" of "alleen als" niet genoeg is.
Jij zegt dat "A alleen als B" alleen betekent dat B impliceert A (wat trouwens fout is volgens de link in de edit, precies andersom), maar dan had ik net zo goed het woordje "alleen" weg kunnen laten. Dan krijg je "A als B". Volgens jou is "A alleen als B" en "A als B" dus hetzelfde, en dat vind ik raar. Het woordje "alleen" erbij geeft in mijn ogen aan dat het in andere gevallen niet zo is. Dus als B niet geldt, dan geldt A ook niet. En dat is equivalent met "A impliceert B". Dus dan zijn A en B equivalent. Wat klopt er niet aan deze redenering?
edit:
Nog steeds vind ik het niet echt logisch. Ik heb even een discussie hierover gevonden in het Engels.
http://forums.philosophyf(...)d-only-if-27842.html
Daar wordt als voorbeeld gegeven dat "Ik slaag alleen als ik meer dan 50 punten heb" nog steeds kan betekenen dat je met 51 punten zakt. Dat vind ik een beetje raar klinken.
Het zit hem in het feit dat ik "alleen als" zie als een sterkere uitspraak dan "als". Dus "alleen als" impliceert "als". Blijkbaar vindt men dat dat niet zo is
Beneath the gold, bitter steel
