SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Veel bewijzen uit het eerste jaar kan ik nu zo opschrijven omdat ze helemaal niet zo lastig zijn. Af en toe kijk ik terug, en af en toe maakt het mij niet uit. Jouw transposevoorbeeld zou ik zo uitschrijven door te kijken waaraan element (i,j) gelijk is, maar die moeite zou ik niet nemen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Je zou die transposeregel even snel kunnen checken met twee 2x2 matrices bijvoorbeeld, zodat je wat meer inzicht hebt hoe het in elkaar zit. Dat kan je dan algemeen gaan opschrijven maar dat is gewoon geen leuk klusje. 
Valt wel mee, één regeltje met 3 gelijkheidstekens.quote:Op donderdag 4 augustus 2011 21:09 schreef thenxero het volgende:
Dat kan je dan algemeen gaan opschrijven maar dat is gewoon geen leuk klusje.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Klopt maar het klooien met indices of matrixelementen vind/vond ik nooit leukquote:
[..]
Valt wel mee, één regeltje met 3 gelijkheidstekens.
Als je bang bent voor indices dan heb je het niet vaak genoeg gedaan.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ben niet bang maar vind het gewoon saai.quote:Op donderdag 4 augustus 2011 22:53 schreef GlowMouse het volgende:
Als je bang bent voor indices dan heb je het niet vaak genoeg gedaan.
Inderdaad, zolang je die dingen niet kan dromen ken je het nog nietquote:
Als je bang bent voor indices dan heb je het niet vaak genoeg gedaan.
Beneath the gold, bitter steel
Ik ben bezig met een opgave, maar ik zie even niet wat ze doen.
Het gaat om deze:
(1/5)q1-(4/5) q2(3/5)
(3/5)qq(1/5) q2-(2/5)
(een breuk dus)
Ze maken daar het volgende van:
q2
3q1
Maar ik zie niet hoe ze daar aan komen. Ok, ik begrijp dat je die eerste met 5 kunt vermenigvuldigen, maar ik kom dan op
q1-4q23
3q1q2-2
uit. Wat mis ik dat ze doen?
(sorry voor de onduidelijke manier van neerzetten, vond dit al moeilijk genoeg)
[ Bericht 0% gewijzigd door maen op 07-08-2011 11:31:44 ]
Het gaat om deze:
(1/5)q1-(4/5) q2(3/5)
(3/5)qq(1/5) q2-(2/5)
(een breuk dus)
Ze maken daar het volgende van:
q2
3q1
Maar ik zie niet hoe ze daar aan komen. Ok, ik begrijp dat je die eerste met 5 kunt vermenigvuldigen, maar ik kom dan op
q1-4q23
3q1q2-2
uit. Wat mis ik dat ze doen?
(sorry voor de onduidelijke manier van neerzetten, vond dit al moeilijk genoeg
)[ Bericht 0% gewijzigd door maen op 07-08-2011 11:31:44 ]
Bedenk dat: x -y = 1 / (x y)quote:
Ik ben bezig met een opgave, maar ik zie even niet wat ze doen.
Het gaat om deze:
(1/5)q1-(4/5) q2(3/5)
(3/5)qq(1/5) q2-(2/5)
(een breuk dus)
Ze maken daar het volgende van:
q2
3q1
Maar ik zie niet hoe ze daar aan komen. Ok, ik begrijp dat je die eerste met 5 kunt vermenigvuldigen, maar ik kom dan op
q1-4q23
3q1q2-2
uit. Wat mis ik dat ze doen?
(sorry voor de onduidelijke manier van neerzetten, vond dit al moeilijk genoeg
En: x a . xb = x (a+b)
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
Hmm bedankt, maar dan zie ik het nog niet..quote:
[..]
Bedenk dat: x -y = 1 / (x y)
En: x a . xb = x (a+b)
Ik heb de volgende opdracht:
syntax = u'x = du/dx
"Find dz expressed in terms of dx and dy when u = u(x,y)."
z = (x^2)*u
Ik gebruik de definitie dz = (z'x) * (dx) + (z'u) * (du)
Dan ga ik invullen:
Aangezien u een functie is van x gebruik ik de ketting regel.
z'x = (z'x)* (x') + (z'u) * (u'x)
z'x = (2xu) * 1 + (x^2)* (u'x)
du = (dx) * (u'x) + (dy) * (u'y)
z'u = x^2
Dit invullen:
dz = ((2xu) * 1 + (x^2)* (u'x)) * (dx) + (x^2) * ((dx) * (u'x) + (dy) * (u'y))
dz = (2xu)*(dx) + (x^2)*(u'x)*(dx) + (x^2)*(dx)*(u'x) + (dy)*(x^2)*(u'y)
dz = (2xu)*(dx) + 2(x^2)*(u'x)*(dx) + (dy)*(x^2)*(u'y)
dz = (2xu)*(dx) + (x^2)*(2*(u'x)*(dx) + (dy)*(u'y))
Nu is het goede antwoord volgens het antwoordenboek bijna hetzelfde namelijk:
dz = (2xu)*(dx) + (x^2)*((u'x)*(dx) + (dy)*(u'y))
Ik doe dus iets fout, alleen geen idee waar.
Ook heb ik het gevoel dat ik nogal lang bezig ben met een relatief makkelijke formule.
Methode 2:
Ik heb net een andere methode geprobeerd door gebruik te maken van de differential regels.
z = (x^2)*(u)
dz = d((x^2)*(u))
Definitie:
d((f)*(g)) = d(f)*(g) + d(g)*(f)
= d(x^2)* (u) + d(u) * (x^2)
= (2xu)*(dx)*(x^2) * ( (dy)* (u'y) + (dx) * (u'x))
Dan komt hij wel uit, snap echter nog steeds niet waarom het via methode 1 niet werkt.
[ Bericht 60% gewijzigd door JohnSpek op 07-08-2011 12:10:47 ]
syntax = u'x = du/dx
"Find dz expressed in terms of dx and dy when u = u(x,y)."
z = (x^2)*u
Ik gebruik de definitie dz = (z'x) * (dx) + (z'u) * (du)
Dan ga ik invullen:
Aangezien u een functie is van x gebruik ik de ketting regel.
z'x = (z'x)* (x') + (z'u) * (u'x)
z'x = (2xu) * 1 + (x^2)* (u'x)
du = (dx) * (u'x) + (dy) * (u'y)
z'u = x^2
Dit invullen:
dz = ((2xu) * 1 + (x^2)* (u'x)) * (dx) + (x^2) * ((dx) * (u'x) + (dy) * (u'y))
dz = (2xu)*(dx) + (x^2)*(u'x)*(dx) + (x^2)*(dx)*(u'x) + (dy)*(x^2)*(u'y)
dz = (2xu)*(dx) + 2(x^2)*(u'x)*(dx) + (dy)*(x^2)*(u'y)
dz = (2xu)*(dx) + (x^2)*(2*(u'x)*(dx) + (dy)*(u'y))
Nu is het goede antwoord volgens het antwoordenboek bijna hetzelfde namelijk:
dz = (2xu)*(dx) + (x^2)*((u'x)*(dx) + (dy)*(u'y))
Ik doe dus iets fout, alleen geen idee waar.
Ook heb ik het gevoel dat ik nogal lang bezig ben met een relatief makkelijke formule.
Methode 2:
Ik heb net een andere methode geprobeerd door gebruik te maken van de differential regels.
z = (x^2)*(u)
dz = d((x^2)*(u))
Definitie:
d((f)*(g)) = d(f)*(g) + d(g)*(f)
= d(x^2)* (u) + d(u) * (x^2)
= (2xu)*(dx)*(x^2) * ( (dy)* (u'y) + (dx) * (u'x))
Dan komt hij wel uit, snap echter nog steeds niet waarom het via methode 1 niet werkt.
[ Bericht 60% gewijzigd door JohnSpek op 07-08-2011 12:10:47 ]
z'x = 2xuquote:
Ik heb de volgende opdracht:
syntax = u'x = du/dx
"Find dz expressed in terms of dx and dy when u = u(x,y)."
z = (x^2)*u
Ik gebruik de definitie dz = (z'x) * (dx) + (z'u) * (du)
Dan ga ik invullen:
Aangezien u een functie is van x gebruik ik de ketting regel.
z'x = (z'x)* (x') + (z'u) * (u'x)
z'x = (2xu) * 1 + (x^2)* (u'x)
du = (dx) * (u'x) + (dy) * (u'y)
z'u = x^2
Dit invullen:
dz = ((2xu) * 1 + (x^2)* (u'x)) * (dx) + (x^2) * ((dx) * (u'x) + (dy) * (u'y))
dz = (2xu)*(dx) + (x^2)*(u'x)*(dx) + (x^2)*(dx)*(u'x) + (dy)*(x^2)*(u'y)
dz = (2xu)*(dx) + 2(x^2)*(u'x)*(dx) + (dy)*(x^2)*(u'y)
dz = (2xu)*(dx) + (x^2)*(2*(u'x)*(dx) + (dy)*(u'y))
Nu is het goede antwoord volgens het antwoordenboek bijna hetzelfde namelijk:
dz = (2xu)*(dx) + (x^2)*(*(u'x)*(dx) + (dy)*(u'y))
Ik doe dus iets fout, alleen geen idee waar.
Ook heb ik het gevoel dat ik nogal lang bezig ben met een relatief makkelijke formule.
z'u doe je wel goed
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
Mmmh dan haal ik iets door de war.quote:
Zou je kunnen uitleggen waarom z'x = 2xu
(u) hangt toch af van (x), waarom beschouw je (u) hier als constante?
dz/dx = 2 x u + x² du/dx
Ik vind je notaties een beetje vaag dus dat is lastig te lezen zo. De kettingregel is trouwens geen definitie, maar kan je gewoon bewijzen vanuit de definitie van de afgeleide. Ik vind de opgave sowieso vreemd dat je infinitesimalen moet uitdrukken in andere infinitesimalen...
Ik vind je notaties een beetje vaag dus dat is lastig te lezen zo. De kettingregel is trouwens geen definitie, maar kan je gewoon bewijzen vanuit de definitie van de afgeleide. Ik vind de opgave sowieso vreemd dat je infinitesimalen moet uitdrukken in andere infinitesimalen...
Oke dat dacht ik inderdaad ook, ik zal eens even kijken of ik de notatie wat makkelijker kan maken *moment*quote:
dz/dx = 2 x u + x² du/dx
Ik vind je notaties een beetje vaag dus dat is lastig te lezen zo. De kettingregel is trouwens geen definitie, maar kan je gewoon bewijzen vanuit de definitie van de afgeleide. Ik vind de opgave sowieso vreemd dat je infinitesimalen moet uitdrukken in andere infinitesimalen...
Oh of bedoel je met dx dy en dz soms de afgeleiden naar x, y resp z?
En met z'x de afgeleide van z naar x?
En met z'x de afgeleide van z naar x?
met dx bedoel ik een (kleine) verandering van x. (of tenminste, zo bedoelt het boek het)quote:Op zondag 7 augustus 2011 12:42 schreef thenxero het volgende:
Oh of bedoel je met dx dy en dz soms de afgeleiden naar x, y resp z?
En met z'x de afgeleide van z naar x?
met z'x bedoel ik inderdaad de afgeleide van z naar x.
Het lukt me niet om het in mooiere syntax weer te geven.
[ Bericht 92% gewijzigd door JohnSpek op 07-08-2011 13:46:47 ]
[ Bericht 92% gewijzigd door JohnSpek op 07-08-2011 13:46:47 ]
Dat klopt niet, jij doet de breuk tot de vijfde macht en dan staat er wat anders.quote:
Ok, ik begrijp dat je die eerste met 5 kunt vermenigvuldigen, maar ik kom dan op
q1-4q23
3q1q2-2
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
ow, oeps. Maar met die machten hoef ik dan niets te doen?quote:
[..]
Dat klopt niet, jij doet de breuk tot de vijfde macht en dan staat er wat anders.
Het gaat fout als jij hier z'x gaat bepalen: je moet u dan als constant beschouwen.quote:
Ik heb de volgende opdracht:
syntax = u'x = du/dx
"Find dz expressed in terms of dx and dy when u = u(x,y)."
z = (x^2)*u
Ik gebruik de definitie dz = (z'x) * (dx) + (z'u) * (du)
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Als je teller en noemer keer vijf doet dan blijft er hetzelfde staan (maar ben je de 1/5 kwijt en 3/5 wordt 3). De machten blijven wel hetzelfde. Wat Nelis89 zegt dus.quote:Op zondag 7 augustus 2011 13:49 schreef maen het volgende:
[..]
ow, oeps. Maar met die machten hoef ik dan niets te doen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
ah, dan weet ik waar het mis gegaan is. danku!quote:
[..]
Als je teller en noemer keer vijf doet dan blijft er hetzelfde staan (maar ben je de 1/5 kwijt en 3/5 wordt 3). De machten blijven wel hetzelfde. Wat Nelis89 zegt dus.
Ik vermoed dat ik weet waar ik fout ga:quote:
[..]
Het gaat fout als jij hier z'x gaat bepalen: je moet u dan als constant beschouwen.
bij de formule dz = z'x * dx + z'u * du
Hier is z'x de partiële afgeleide van z naar u, waar je u dan constant houdt ook al is u een functie van x.
De regel die ik gebruikte om z'x te bepalen (z'x = (z'x)* (x') + (z'u) * (u'x)) is een regel voor de totale afgeleide van z naar x toe, dus niet de partiële.
De definitie z'x = (z'x)* (x') + (z'u) * (u'x) zegt dus:
De totale afgeleide van z naar x = de partiele afgeleide van z naar x * afgeleide van x naar x + de partiele afgeleide van z naar y * afgeleide van u naar x.
Klopt dit wat ik nu zeg?
Held!quote:Op vrijdag 29 juli 2011 21:48 schreef GlowMouse het volgende:
Vanaf nu kun je met de [tex]-tag Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Zie nu pas dat we latex kunnen gebruiken! Erg mooi, Glowmouse!
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Ik ben bezig met een wiskunde opfriscursus en ben nu bij het onderwerp differentieren beland. Ik heb het vroeger allemaal gehad en had er nooit problemen mee, maar er is een vraag die ik niet echt begrijp.
Hij luidt als volgt:
Voor de differentieerbare functie f geldt dat:
f(x) = 10x^2 + 2x + 5 als x ≤ 1.
Voor x>1 geldt dat f(x)=a⋅x+b voor constanten a en b.
Wat zijn de waarden van a en b? Wat is het functievoorschrift f(x) voor x>1?
Voor x>1 geldt f(x)= [hier je antwoord]
Bij 'tips' staat het volgende over dit 'probleem':
Kies de waarden van a en b zo, dat in het punt x=1 de functie 10⋅x2+2⋅x+5
en a⋅x+b dezelfde waarde aannemen en dezelfde afgeleide hebben.
En de oplossing is:
Voor x groter dan 1 is de vergelijking
f(x)=22⋅x+−5.
Ik weet hier echt niet wat ze precies bedoelen en vroeger op het vwo had ik ook nooit zoiets gehad, het was altijd simpelweg een formule krijgen en daar moest je dan de afgeleide van bepalen.
Mijn vraag gaat dus niet zozeer over hoe je moet differentieren en wat de regels daarbij zijn, maar meer over wat er hier bedoeld wordt.
Bij voorbaat dank!
PS: het is een online cursus dus ik heb geen leraar aan wie ik het kan vragen.
Hij luidt als volgt:
Voor de differentieerbare functie f geldt dat:
f(x) = 10x^2 + 2x + 5 als x ≤ 1.
Voor x>1 geldt dat f(x)=a⋅x+b voor constanten a en b.
Wat zijn de waarden van a en b? Wat is het functievoorschrift f(x) voor x>1?
Voor x>1 geldt f(x)= [hier je antwoord]
Bij 'tips' staat het volgende over dit 'probleem':
Kies de waarden van a en b zo, dat in het punt x=1 de functie 10⋅x2+2⋅x+5
en a⋅x+b dezelfde waarde aannemen en dezelfde afgeleide hebben.
En de oplossing is:
Voor x groter dan 1 is de vergelijking
f(x)=22⋅x+−5.
Ik weet hier echt niet wat ze precies bedoelen en vroeger op het vwo had ik ook nooit zoiets gehad, het was altijd simpelweg een formule krijgen en daar moest je dan de afgeleide van bepalen.
Mijn vraag gaat dus niet zozeer over hoe je moet differentieren en wat de regels daarbij zijn, maar meer over wat er hier bedoeld wordt.
Bij voorbaat dank!
PS: het is een online cursus dus ik heb geen leraar aan wie ik het kan vragen.
Wat ze dus willen is dat je je constanten a en b zodanig kiest dat de functies f(x) = 10x^2 + 2x + 5 en ax+b naadloos op elkaar aansluiten. Even officiëler gezegd, dat er aan de continuïteits- èn differentieerbaarheidsvoorwaaden voldaan wordt op het punt P(1,17)
we hebben f(x) = 10x^2 + 2x + 5; dit geeft als afgeleide f '(x) = 20x + 2
we hebben ook f(x) = ax+b; dit geeft als afgeleide simpelweg f '(x) = a
Eerst gaan we aan de slag met de afgeleiden; we nemen de linkerlimiet van 20x + 2 voor x -> 1 => 20*1 + 2 = 22. Hieruit kun je direct concluderen dat de constante a in de functie f(x) = ax+b dus 22 moet zijn; after all, f '(x) = a = 22.
nu we weten dat a = 22, kunnen de oorspronkelijke functies onder handen nemen. We nemen wederom de linkerlimiet, dit keer van 10x^2 + 2x + 5 voor x -> 1 => f(x) = 17
nu pluggen we alles in a*x +b = y in.
a = 22 (je richtingscoëfficiënt die adhv je afgeleiden bepaald hebt)
x = 1 (dat is de x-coördinaat van het punt waar de functies naadloos op elkaar moeten aansluiten)
y = 22 (kan je direct berekenen door in f(x) de waarde 1 in te vullen)
22*1 + b = 17 => b = -5
[ Bericht 19% gewijzigd door VanishedEntity op 14-08-2011 21:01:41 ]
we hebben f(x) = 10x^2 + 2x + 5; dit geeft als afgeleide f '(x) = 20x + 2
we hebben ook f(x) = ax+b; dit geeft als afgeleide simpelweg f '(x) = a
Eerst gaan we aan de slag met de afgeleiden; we nemen de linkerlimiet van 20x + 2 voor x -> 1 => 20*1 + 2 = 22. Hieruit kun je direct concluderen dat de constante a in de functie f(x) = ax+b dus 22 moet zijn; after all, f '(x) = a = 22.
nu we weten dat a = 22, kunnen de oorspronkelijke functies onder handen nemen. We nemen wederom de linkerlimiet, dit keer van 10x^2 + 2x + 5 voor x -> 1 => f(x) = 17
nu pluggen we alles in a*x +b = y in.
a = 22 (je richtingscoëfficiënt die adhv je afgeleiden bepaald hebt)
x = 1 (dat is de x-coördinaat van het punt waar de functies naadloos op elkaar moeten aansluiten)
y = 22 (kan je direct berekenen door in f(x) de waarde 1 in te vullen)
22*1 + b = 17 => b = -5
[ Bericht 19% gewijzigd door VanishedEntity op 14-08-2011 21:01:41 ]
Maar de vraag doet toch een heleboel aannames? Waarom kan x > 1 niet gewoon een andere richtingscoëfficiënt hebben?
Er staat "differentieerbare functie". Deze samengestelde functie f(x) = 10x^2 + 2x + 5 voor x ≤ 1 EN f(x) = ax+b voor x>1 moet in het punt P(1, 17):quote:
Maar de vraag doet toch een heleboel aannames? Waarom kan x > 1 niet gewoon een andere richtingscoëfficiënt hebben?
- zowel continu ( lim x↑1 f(x) = lim x↓1 f(x) )
- als differentieerbaar (lim x↑1 f '(x) = lim x↓1 f '(x) )
zijn.
[ Bericht 0% gewijzigd door VanishedEntity op 14-08-2011 21:01:29 ]
Nee, zoals VE al aangaf maar dan simpeler verwoord: de functie heeft dan in het punt x=1 een knak en is daar dan niet diff'baar. Verder moet je ervoor zorgen dat de functie na x=1 geen sprongetje maakt, want dan is hij niet meer continu en dus niet meer differentieerbaar (differentieerbaarheid impliceert continuïteit). Met die twee voorwaarden van gelijke afgeleide en gelijke functiewaarde in het punt 1 kan je dus a en b afleiden.quote:
Maar de vraag doet toch een heleboel aannames? Waarom kan x > 1 niet gewoon een andere richtingscoëfficiënt hebben?
Je moet gewoon zorgen dat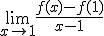 
bestaat.
Je notatie is raar, maar je lijkt hier continu differentieerbaar te schrijven, en dat is een strengere eis.quote:
[..]
- als differentieerbaar (lim x↑1 f '(x) = lim x↓1 f '(x) )
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
En dat doe je door zowel de linkerlimiet als de rechterlimiet te berekenen en te verifiëren dat die 2 uitkomsten aan elkaar gelijk zijn.quote:
Ik weet niet wat jouw probleem is maar lim x↑a voor de linkerlimiet en lim x↓a voor de rechterlimiet zijn echt heel gebruikelijke notaties (pakt zn Wiskunde B examen en samenvattingen boekje er nog eens bij). En dr staan echt wel accenten bij de f-jes op de regel die de differentieerbaarheidseis vermeldt.quote:Je notatie is raar, maar je lijkt hier continu differentieerbaar te schrijven, en dat is een strengere eis.
Oh, het is subscript. De 1 lijkt bij mij veel op een pijltje omhoog. Je eist nu dat de afgeleide continu is, en dat is meer dan differentieerbaarheid alleen; zie voor een voorbeeld http://en.wikipedia.org/w(...)rentiability_classes
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
In het punt waar de functie van het ene voorschift in het andere voorschift overgaat (in dit geval x=1 => P(1,17) ) moet hij volgens de opgave zowel continu als differentieerbaar zijn. Wat de functievoorschriften in punten voor andere waarden van x en daarmee y doen is niet van belang.quote:
Oh, het is subscript. De 1 lijkt bij mij veel op een pijltje omhoog. Je eist nu dat de afgeleide continu is, en dat is meer dan differentieerbaarheid alleen; zie voor een voorbeeld http://en.wikipedia.org/w(...)rentiability_classes
Precies, maar de afgeleide zelf hoeft niet continu te zijn.quote:
[..]
In het punt waar de functie van het ene voorschift in het andere voorschift overgaat (in dit geval x=1 => P(1,17) ) moet hij volgens de opgave zowel continu als differentieerbaar zijn. Wat de functievoorschriften in punten voor andere waarden van x en daarmee y doen is niet van belang.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
