SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Ik heb een (simpel?) statistiek vraagje, waarbij je wat concepten nodig hebt die voor mij al een tijdje geleden zijn.
Stel, ik heb de verzameling reëele getallen R. Ik neem een eindige deelverzameling X en een eindige deelverzameling Y van R, waarbij het aantal elementen |X| van de verzameling X groter is dan het aantal elementen |Y| van de verzameling Y:
|X|>|Y|
Nu ga je een willekeurig getal in R genereren. Is de kans dat dit getal in X ligt nu groter dan in Y? Mijn gevoel zegt van niet, aangezien volgens mij zowel X als Y maat 0 hebben in R. Klopt deze naïeve redenatie?
En zou dit ook gelden als X en Y beide oneindig zijn, maar wel aftelbaar, met verschillende kardinaliteiten?
Stel, ik heb de verzameling reëele getallen R. Ik neem een eindige deelverzameling X en een eindige deelverzameling Y van R, waarbij het aantal elementen |X| van de verzameling X groter is dan het aantal elementen |Y| van de verzameling Y:
|X|>|Y|
Nu ga je een willekeurig getal in R genereren. Is de kans dat dit getal in X ligt nu groter dan in Y? Mijn gevoel zegt van niet, aangezien volgens mij zowel X als Y maat 0 hebben in R. Klopt deze naïeve redenatie?
En zou dit ook gelden als X en Y beide oneindig zijn, maar wel aftelbaar, met verschillende kardinaliteiten?
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Dat is kansrekening, en je redenering met de kansmaat klopt. Beide kansen zijn 0. Ook bij aftelbare verzamelingen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Da's een snel antwoord, dank je welquote:Op zaterdag 16 april 2011 21:55 schreef GlowMouse het volgende:
Dat is kansrekening, en je redenering met de kansmaat klopt. Beide kansen zijn 0. Ook bij aftelbare verzamelingen.
Ik zal es opzoeken hoe je dit precies beredeneert 
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Hallo,
Zij X1, X2, ... geometrische stochastische variabelen met parameter a. Zij N Fs verdeeld (Fs= first succes, d.w.z. p(X=k) = p (1-p)k-1). Stel dat alle stochastische variabelen onafhankelijk zijn en zet Y=X1 + ... + XN.
Ik moet laten zien dat Y geometrisch verdeeld is met een bepaalde parameter b die ik ook moet bepalen.
Ik denk dat ik kan gebruiken dat phiY (t) = gN(phiX(t)), waarbij phi staat voor de karakteristieke functie en g voor de kansgenererende functie.
Ik gebruik dat phiX(t) = a/(1-(1-a)eit) en de definitie van de kansgenererende functie: gN(t) = sum_{n=0}^{\infty} tn P(N=n) = sum_{n=0}^{\infty} tn p(1-p)n-1.
Als ik vervolgens phiX in gN(t) ga invullen dan krijg ik een best lelijke uitdrukking waaruit ik niet kan opmaken dat Y geometrisch verdeeld is. Klopt mijn aanpak een beetje of doe ik het verkeerd?
Alvast bedankt.
Zij X1, X2, ... geometrische stochastische variabelen met parameter a. Zij N Fs verdeeld (Fs= first succes, d.w.z. p(X=k) = p (1-p)k-1). Stel dat alle stochastische variabelen onafhankelijk zijn en zet Y=X1 + ... + XN.
Ik moet laten zien dat Y geometrisch verdeeld is met een bepaalde parameter b die ik ook moet bepalen.
Ik denk dat ik kan gebruiken dat phiY (t) = gN(phiX(t)), waarbij phi staat voor de karakteristieke functie en g voor de kansgenererende functie.
Ik gebruik dat phiX(t) = a/(1-(1-a)eit) en de definitie van de kansgenererende functie: gN(t) = sum_{n=0}^{\infty} tn P(N=n) = sum_{n=0}^{\infty} tn p(1-p)n-1.
Als ik vervolgens phiX in gN(t) ga invullen dan krijg ik een best lelijke uitdrukking waaruit ik niet kan opmaken dat Y geometrisch verdeeld is. Klopt mijn aanpak een beetje of doe ik het verkeerd?
Alvast bedankt.
De opgave was toch echt om te laten zien dat Y geometrisch verdeeld is.... Maar klopt mijn aanpak wel en heb jij op die manier laten zien dat Y negatief binomiaal verdeeld is?
edit: Volgens mij heb je er geen rekening mee gehouden dat N ook nog een stochastische variabele is...? Anders doe je inderdaad de karakteristieke functie van de geometrische verdeling tot de n-de macht en dan verkrijg je de karakteristieke functie voor de negatieve binomiale verdeling.
edit: Volgens mij heb je er geen rekening mee gehouden dat N ook nog een stochastische variabele is...? Anders doe je inderdaad de karakteristieke functie van de geometrische verdeling tot de n-de macht en dan verkrijg je de karakteristieke functie voor de negatieve binomiale verdeling.
Ah, N is een stochast. Dan had je beter P(N=k) kunnen schrijven.
Die aanpak werkt nog steeds, behalve dat je dan nog de N eruit moet sommeren (P(Y=k) = E(P(Y=k | N))quote:
edit: Volgens mij heb je er geen rekening mee gehouden dat N ook nog een stochastische variabele is...? Anders doe je inderdaad de karakteristieke functie van de geometrische verdeling tot de n-de macht en dan verkrijg je de karakteristieke functie voor de negatieve binomiale verdeling.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Wat moet het nu uiteindelijk worden? En waarom? Want het lukt me zelfs niet om te vinden met mijn boek erbij.quote:
[..]
0.32^2 = 0,1024 kan ik ook zo zeggen, dat is altijd waar. Maar je wilt P(B) weten. P(A)P(A|B) = P(B)P(B|A)
nu het gegeven gebruiken dat P(A|B) = P(B|A) (!= 0)
P(A)P(A|B) = P(B)P(A|B)
en nu weet je P(A)=0.32.
Je hebt gelijk, typfoutje.quote:
Ah, N is een stochast. Dan had je beter P(N=k) kunnen schrijven.
Deze formule ken ik niet... Waar komt dat vandaan?quote:Die aanpak werkt nog steeds, behalve dat je dan nog de N eruit moet sommeren (P(Y=k) = E(P(Y=k | N))
edit: of staat E soms voor de som, en niet voor expected value?
Pak P(A)P(A|B) = P(B)P(A|B) en deel door P(A|B).quote:
[..]
Wat moet het nu uiteindelijk worden? En waarom? Want het lukt me zelfs niet om te vinden met mijn boek erbij.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
E is uiteraard expectation; http://en.wikipedia.org/wiki/Conditioning_%28probability%29quote:
Deze formule ken ik niet... Waar komt dat vandaan?
edit: of staat E soms voor de som, en niet voor expected value?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Die formule vind ik niet terug op die wikipagina.quote:
[..]
E is uiteraard expectation; http://en.wikipedia.org/wiki/Conditioning_%28probability%29
Ah, ik ken die formule wel alleen dan in een andere vorm. Nevermind...
Het idee is dus dat je het volgende doet:
P(y=k) = E(P(Y=k) | N) = E( [(N+k-1)nCr k] aN (1-a)k ),
om dat vervolgens met de definitie van de verwachtingswaarde te berekenen?
Dit wil ik wel proberen, maar dit heeft niks met mijn aanpak te maken en het wordt denk ik een erg omslachtige berekening. Heb je enig idee of er bij mijn methode iets mis ging?
P(y=k) = E(P(Y=k) | N) = E( [(N+k-1)nCr k] aN (1-a)k ),
om dat vervolgens met de definitie van de verwachtingswaarde te berekenen?
Dit wil ik wel proberen, maar dit heeft niks met mijn aanpak te maken en het wordt denk ik een erg omslachtige berekening. Heb je enig idee of er bij mijn methode iets mis ging?
Als je formules juist zijn, haal je een p/(1-p) voor de som en heb je een mooie meetkundige reeks. Dat is toch niet zo lelijk?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Klopt, valt nog wel mee. Dan krijg ik gN(t) = [p/(1-p)] * [(1-(t-tp)n)/(1-t+tp)]. Maar dan moet ik nog t->a/(1-(1-a)eit) gaan invullen en dat wordt niet leuk. Volgens mathematica komt er zo te zien niet het goede antwoord uit...quote:
Als je formules juist zijn, haal je een p/(1-p) voor de som en heb je een mooie meetkundige reeks. Dat is toch niet zo lelijk?
http://www.wolframalpha.c(...)C++++0%2C+Infinity}]
Om een willekeurig getal in R te genereren, moet je eerst een kansverdeling op R aangeven aan de hand waarvan je het willekeurige getal genereert.quote:
Nu ga je een willekeurig getal in R genereren.
In hoeverre is die kansverdeling van invloed op de eindconclusie?quote:
[..]
Om een willekeurig getal in R te genereren, moet je eerst een kansverdeling op R aangeven aan de hand waarvan je het willekeurige getal genereert.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
De invloed is er als niet elke waarde in R aangenomen kan worden.quote:
[..]
In hoeverre is die kansverdeling van invloed op de eindconclusie?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Wel, er zijn kansverdelingen waarbij sommige elementen een positieve kans hebben.quote:
[..]
De invloed is er als niet elke waarde in R aangenomen kan worden.
Kun je een voorbeeld geven?quote:
[..]
Wel, er zijn kansverdelingen waarbij sommige elementen een positieve kans hebben.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
X={1,2}
Y = {2,3,4}
Definieer Z als:
- N(0,1) verdeeld met kans 0.5
- 1 met kans 0.5.
Dit soort gemengde continu/discrete verdelingen komt tevoorschijn bij censored regressiemodellen.
[ Bericht 6% gewijzigd door GlowMouse op 18-04-2011 09:37:04 ]
Y = {2,3,4}
Definieer Z als:
- N(0,1) verdeeld met kans 0.5
- 1 met kans 0.5.
Dit soort gemengde continu/discrete verdelingen komt tevoorschijn bij censored regressiemodellen.
[ Bericht 6% gewijzigd door GlowMouse op 18-04-2011 09:37:04 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik ben bezig met differentiëren volgens de quotiëntregel en nu kloppen mijn antwoorden allemaal, alleen is de vorm nog niet genoeg vereenvoudigd. Echter zou ik niet weten hoe/via welke methode ik van het antwoord op onderstaande formule de uiteindelijke formule krijg. Wie kan mij dit vertellen?
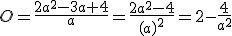
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Ik weet niet wat jij doet, maar ik zou je rekenregels omtrent breuken nog maar es goed doornemen
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Verrek. Hij is eenvoudiger dan ik had verwacht. Bedankt!quote:
[ afbeelding ]
Ik weet niet wat jij doet, maar ik zou je rekenregels omtrent breuken nog maar es goed doornemen
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
P(A)P(A|B) = 0.32 x 0.32quote:
[..]
Pak P(A)P(A|B) = P(B)P(A|B) en deel door P(A|B).
P(A|B) = 0.32
Dus (0.32 x 0.32) / 0.32 = 0.32?
In de vraag was niet gegeven dat P(A|B) = 0.32.quote:
[..]
P(A)P(A|B) = 0.32 x 0.32
P(A|B) = 0.32
Dus (0.32 x 0.32) / 0.32 = 0.32?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik weet het niet danquote:
[..]
In de vraag was niet gegeven dat P(A|B) = 0.32.
Het is echt heel simpel:quote:
P(A)P(B|A) = P(A en B)= P(B)P(A|B)
P(B|A)=P(A|B) geeft:
P(A)P(A|B) = P(B)P(A|B)
en dus
P(A)=P(B)
En het is gegeven dat P(A)=0.32, dus P(B)=0.32.
Som 1: 2(x2-3x-24)=16
1e stap: 2(x2-3x-10)=2
2e stap: x2-3x-10
A: 1
B: -3
C: -10
(3)2-(4x1x-10) = D= -360
Ik kom er dus niet uit, zoals je ziet
1e stap: 2(x2-3x-10)=2
2e stap: x2-3x-10
A: 1
B: -3
C: -10
(3)2-(4x1x-10) = D= -360
Ik kom er dus niet uit, zoals je ziet
Je wilt een kwadratische vergelijking oplossen?quote:
Som 1: 2(x2-3x-24)=16
1e stap: 2(x2-3x-10)=2
2e stap: x2-3x-10
A: 1
B: -3
C: -10
(3)2-(4x1x-10) = D= -360
Ik kom er dus niet uit, zoals je ziet
Ik zou eerst gezamelijke factoren wegdelen; hier is dat 2, dan krijg je
Dan haal je de 8 naar de andere kant, en krijg je
Nu kun je de ABC formule er op loslaten, met A=1, B=-3, C=-16 (mintekens niet vergeten!):
Zou zelf wel ff narekenen op rekenfouten
Je had natuurlijk ook gelijk de ABC formule op
kunnen loslaten (haken uitwerken, en de 16 naar links halen). Het eindantwoord is dan hetzelfde, zoals je zelf kunt checken.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Inderdaad Haus, kijk nog maar eens goed ...quote:
[..]
Zou zelf wel ff narekenen op rekenfouten
Ja, ik zie het al, -24-8 is plots -16 geworden, moet -32 zijn.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
De meeste mensen zijn risico avers, dit betekent dat ze liever 50 euro met zekerheid ontvangen dan 0 euro met kans een 0,5 en 100 euro met kans 0,5.
Het bedrag dat Klaas kan ontvangen hangt af van het toeval, bij de onderstaande vragen is de kansverdeling van de mogelijke bedragen gegeven. Als het gemiddelde van de kansverdelingen wordt weergegeven door µ en de standaarddeviatie door , dan is de waarde W die Klaas toekent aan het ontvangen bedrag gelijk aan: W = µ - 0,1 .
b) De kansvariabele (random-) X is binomiaal verdeeld met n = 4 en p = 0,6. Wat is de waarde (W) die Klaas toekent aan het te ontvangen bedrag 25X euro, m.a.w. bereken W(25X)?
np = 2,4
= 0.9798
Wat moet ik nu berekenen?
c) De kansvariabele Y is normaal verdeeld met gemiddelde µ en standaard deviatie . De waarde die Klaas toekent aan het te ontvangen bedrag Y euro is 45 (dus: W(Y)=45). Bovendien is er een kans van 10 procent dat Y groter is dan 100 euro. Bepaal µ en .
Kom tot InvNorm(0.9,45,100) = 173.16 en dan?
Het bedrag dat Klaas kan ontvangen hangt af van het toeval, bij de onderstaande vragen is de kansverdeling van de mogelijke bedragen gegeven. Als het gemiddelde van de kansverdelingen wordt weergegeven door µ en de standaarddeviatie door , dan is de waarde W die Klaas toekent aan het ontvangen bedrag gelijk aan: W = µ - 0,1 .
b) De kansvariabele (random-) X is binomiaal verdeeld met n = 4 en p = 0,6. Wat is de waarde (W) die Klaas toekent aan het te ontvangen bedrag 25X euro, m.a.w. bereken W(25X)?
np = 2,4
= 0.9798
Wat moet ik nu berekenen?
c) De kansvariabele Y is normaal verdeeld met gemiddelde µ en standaard deviatie . De waarde die Klaas toekent aan het te ontvangen bedrag Y euro is 45 (dus: W(Y)=45). Bovendien is er een kans van 10 procent dat Y groter is dan 100 euro. Bepaal µ en .
Kom tot InvNorm(0.9,45,100) = 173.16 en dan?
b) van X weet je dat mu=2,4 en sigma=0.98. Dan weet je dat ook van 25X, en dan kan je W berekenen.
c) 45 = mu - 0,1 sigma, en (100-sigma)/mu = invNorm(0.9). En dan oplossen.
c) 45 = mu - 0,1 sigma, en (100-sigma)/mu = invNorm(0.9). En dan oplossen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
B = 60 en 4.9 dus W = mu(60)- 0,1 x sigma(4,9) dus = 59,51quote:
b) van X weet je dat mu=2,4 en sigma=0.98. Dan weet je dat ook van 25X, en dan kan je W berekenen.
c) 45 = mu - 0,1 sigma, en (100-sigma)/mu = invNorm(0.9). En dan oplossen.
C = Snap niet wat ik moet doen kan je het antwoord vertellen aub, want heb morgen het tentamen
Bedankt voor al je hulp!
B 4,9 klopt niet, dat zou je hebben als je 25 ongecorreleerde X'en op zou tellen.
C reken invNorm(0.9) uit en je hebt twee vergelijkingen
C reken invNorm(0.9) uit en je hebt twee vergelijkingen
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Wie kan mij vertellen hoe ik deze vergelijking kan oplossen? Ontbinden in factoren lijkt mij namelijk niet te werken of ik maak een denkfout. Ik heb het antwoord overigens wel gevonden via mijn GRM, maar ik wil graag weten hoe het zou moeten.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Pak links en rechts de natuurlijke logaritme (dat is een strikt stijgende functie, dus daardoor introduceer je geen extra oplossingen).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Als je doet wat GlowMouse zegt vervalt de exponent en krijg je gewoon 2x = 1-x, -x naar links halen krijg je 3x = 1 -> x = 1/3quote:
Wie kan mij vertellen hoe ik deze vergelijking kan oplossen? Ontbinden in factoren lijkt mij namelijk niet te werken of ik maak een denkfout. Ik heb het antwoord overigens wel gevonden via mijn GRM, maar ik wil graag weten hoe het zou moeten.
[ afbeelding ]
Ik heb een vakantietaak (ja dat bestaat nog) voor wiskunde 
Ik heb vergelijkingen op te lossen naar y.
Bv. 2x+3y =2
3y=-2x=2
y=-2/3x +2/3
Weet iemand een online calculator voor dit?
Ik had een handige site wat dit betreft, maar die ben ik kwijt.
Ik heb vergelijkingen op te lossen naar y.
Bv. 2x+3y =2
3y=-2x=2
y=-2/3x +2/3
Weet iemand een online calculator voor dit?
Ik had een handige site wat dit betreft, maar die ben ik kwijt.
Deze vergelijkingen zijn dusdanig eenvoudig dat je meer tijd kwijt bent met het invoeren ervan en het overnemen van de uitwerkingen dan ze rechtstreeks met pen en papier te herleiden. Bovendien leer je er dan ook nog iets van, en dat zal toch wel de bedoeling zijn van die taak.quote:
Ik heb een vakantietaak (ja dat bestaat nog) voor wiskunde
Ik heb vergelijkingen op te lossen naar y.
Bv. 2x+3y =2
3y=-2x+2
y=-2/3x +2/3
Weet iemand een online calculator voor dit?
Ik had een handige site wat dit betreft, maar die ben ik kwijt.
http://www.wolframalpha.com/quote:
Ik heb een vakantietaak (ja dat bestaat nog) voor wiskunde
Ik heb vergelijkingen op te lossen naar y.
Bv. 2x+3y =2
3y=-2x=2
y=-2/3x +2/3
Weet iemand een online calculator voor dit?
Ik had een handige site wat dit betreft, maar die ben ik kwijt.
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
Bereken BC
Hoe kom ik hier uit?
Dingen die ik mag gebruiken zijn:
1. De stelling van Pythagoras
2. Gelijkvormige driehoeken (snavel- en zandloperfiguren)
3. Goniometrische verhoudingen in rechthoekige driehoeken
4. De 'zijde x hoogte' methode
5. De sinusregel
De uitkomst ligt rond de 60 centimeter.
Onvoldoende gegevens: je kan C willekeurig over de lijn BC verleggen en dan voldoet de configuratie nog altijd aan de gegevens.
Is hoek BAC niet toevallig 90 graden?quote:Op donderdag 21 april 2011 18:17 schreef verwarmingsbank het volgende:
[ afbeelding ]
Bereken BC
Hoe kom ik hier uit?
Dingen die ik mag gebruiken zijn:
1. De stelling van Pythagoras
2. Gelijkvormige driehoeken (snavel- en zandloperfiguren)
3. Goniometrische verhoudingen in rechthoekige driehoeken
4. De 'zijde x hoogte' methode
5. De sinusregel
De uitkomst ligt rond de 60 centimeter.
Nee, want dan zou BC langer zijn dan AB terwijl de vragensteller beweert dat BC ca. 60 cm zou moeten zijn.quote:
[..]
Is hoek BAC niet toevallig 90 graden?
Ik vind dit een boeiende vraag, alleen heb ik geen idee hoe ik moet beginnen.
Kan iemand me op weg helpen? Dan kan ik dan zien of ik genoeg intellect heb om het verder op te kunnen lossen
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
Ik zou zowel positie als verplaatsing in poolcoördinaten uitdrukken, en dan kijken naar de lengte van de som.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Probeer eerst eens de kans te bepalen dat de muis van de tafel afloopt voor een gegeven afstand d van het vertrekpunt van de muis totaan het midelpunt van de tafel. Als de muis precies in het middelpunt van de tafel begint is die kans 0, want dan bereikt hij altijd juist de rand, ongeacht de richting. Als de muis daarentegen start vanaf een punt op de rand, dan is de kans om te eindigen op een punt buiten de tafel 2/3 aangezien alle richtingen even waarschijnlijk zijn en aangezien je dan een hoek hebt van 120 graden tussen de twee radii vanaf het punt op de rand van de tafel naar de snijpunten van de twee cirkels (de tafel met radius 1 meter en de actieradius van 1 meter van de muis vanaf het vertrekpunt op de rand van de tafel).quote:
[ afbeelding ]
Ik vind dit een boeiende vraag, alleen heb ik geen idee hoe ik moet beginnen.
Kan iemand me op weg helpen? Dan kan ik dan zien of ik genoeg intellect heb om het verder op te kunnen lossen
Bedankt voor je reactie, maar het is nog steeds niet goed. In het achterhoofd houden dat het antwoord: -4 of 7 moet zijn, komt deze berekening niet uit.quote:
[..]
Je wilt een kwadratische vergelijking oplossen?
[ afbeelding ]
Ik zou eerst gezamelijke factoren wegdelen; hier is dat 2, dan krijg je
[ afbeelding ]
Dan haal je de 8 naar de andere kant, en krijg je
[ afbeelding ]
Nu kun je de ABC formule er op loslaten, met A=1, B=-3, C=-16 (mintekens niet vergeten!):
[ afbeelding ]
Zou zelf wel ff narekenen op rekenfouten
Je had natuurlijk ook gelijk de ABC formule op
[ afbeelding ]
kunnen loslaten (haken uitwerken, en de 16 naar links halen). Het eindantwoord is dan hetzelfde, zoals je zelf kunt checken.
Ik had het volgende nog geprobeerd:
2(x2-3x-24)=16
2(x2-3x-10)=2^4
x2-3x-10=^4
En dan ABC....?
Of niet?
bedoel je met 2(x2-3x-24) soms 2^(x2-3x-24)?quote:
[..]
Bedankt voor je reactie, maar het is nog steeds niet goed. In het achterhoofd houden dat het antwoord: -4 of 7 moet zijn, komt deze berekening niet uit.
Ik had het volgende nog geprobeerd:
2(x2-3x-24)=16
2(x2-3x-10)=2^4
x2-3x-10=^4
En dan ABC....?
2^(x2-3x-24)=16quote:
[..]
bedoel je met 2(x2-3x-24) soms 2^(x2-3x-24)?
Of niet?
Ok, je had de functie al herleid totquote:
x2-3x-24=4
Dan is de post van Haushofer weer nuttig, want op die methode moet je dit oplossen.
Maar het kan natuurlijk ook zonder de ABC-formule, weet je wat ontbinden in factoren is?
[ Bericht 5% gewijzigd door Siddartha op 22-04-2011 12:26:22 ]
Middag,
Ben al een aantal weken bezig met het herkansen van vastgoed rekenen.
Hoop dat jullie me kunnen helpen, er zit een excel bestand in de bijlage, maar daar zit blijkbaar een fout in die ik er niet uit kan halen, weet iemand het?
http://img841.imageshack.us/i/excelk.jpg/ (copy/paste deze link)
Als je de fout zie, en je wil het excel bestand om het te checken dan kun je me ff pmen.
Ben al een aantal weken bezig met het herkansen van vastgoed rekenen.
Hoop dat jullie me kunnen helpen, er zit een excel bestand in de bijlage, maar daar zit blijkbaar een fout in die ik er niet uit kan halen, weet iemand het?
http://img841.imageshack.us/i/excelk.jpg/ (copy/paste deze link)
Als je de fout zie, en je wil het excel bestand om het te checken dan kun je me ff pmen.
Uhum ja het is misschien wat onduidelijk,
http://img855.imageshack.us/i/excel.jpg/ (copy/paste deze link)
Uploaded with http://imageshack.us (copy/paste deze link)
http://img855.imageshack.us/i/excel.jpg/ (copy/paste deze link)
Uploaded with http://imageshack.us (copy/paste deze link)
Waarde investering snap ik niet. Waarom is er in het eerste jaar geen waardevermeerdering?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Waarinvestering stijgt elk jaar met 2%, en in het 1ste jaar begin je met een start bedrag, die we gekregen hebben.
dan is er in het eerste jaar dus al een stijging.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Vraagje..
Ik heb een bankroll van 20,000, daarvan investeer ik 2.5% (500 dus). Op die 500 maak ik 5% winst, dus 25. Ofwel de return is 525. Bankroll na investering 1 is dus 20,025. Die 20,025 gaat dus via hetzelfde systeem weer in de cycle. Nu wil ik bepalen hoeveel mijn bankroll is na x cycles.
Ik heb een bankroll van 20,000, daarvan investeer ik 2.5% (500 dus). Op die 500 maak ik 5% winst, dus 25. Ofwel de return is 525. Bankroll na investering 1 is dus 20,025. Die 20,025 gaat dus via hetzelfde systeem weer in de cycle. Nu wil ik bepalen hoeveel mijn bankroll is na x cycles.
Je investeert steeds 5% van de 2.5% van het totale bedrag.
0,05 * 0,025 = 0,00125
Bedrag = 20000 * 1,00125 ^ aantal cycli
0,05 * 0,025 = 0,00125
Bedrag = 20000 * 1,00125 ^ aantal cycli
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
Hey nog bedankt, ik heb hem vandaag gehaald bij de biebquote:
[..]
Er zijn legio boeken over getaltheorie geschreven, op alle mogelijke niveaus. Misschien is "Getaltheorie voor beginners" van Frits Beukers iets voor je?
, bevalt wel tot nu toe
Finally, someone let me out of my cage
Iemand die mij misschien wil helpen met uitleggen hoe ze hier van stap 3 naar stap 4 komen?
Het gaat om het ARDL model.
Het gaat om het ARDL model.
Ze herhalen het substitueren van y. De eerste term wordt delta*(1+theta1 + theta1² + ...), en dat is delta/(1-theta1).
In de rest zie je een patroontje dat ze met die som precies overnemen.
In de rest zie je een patroontje dat ze met die som precies overnemen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Hoe kun je makkelijk het kleinst gemeenschappelijke veelvoud vinden van bijvoorbeeld
. Is dat gewoon een kwestie van "proberen" tot dat je hem vindt?
Ik zou ontbinden in factoren. Het kgv moet deelbaar zijn door 8, a, b, a+2, en a²-b.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ok, zo.
8ab = 2*2*2*a*b
8ab+16b = 2*2*2*b(a+2)
En dan moet ik alles samenvoegen en dan krijg ik
Bedankt!
8ab = 2*2*2*a*b
8ab+16b = 2*2*2*b(a+2)
En dan moet ik alles samenvoegen en dan krijg ik
Bedankt!
Inderdaad, alleen krijg je nu bij bv. a=10 een onjuist antwoord.
Bijvoorbeeld met a=10 en b=1 moet je kgv(80, 96, 96) vinden, en dat is geen 80*96.
Bijvoorbeeld met a=10 en b=1 moet je kgv(80, 96, 96) vinden, en dat is geen 80*96.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
GlowMouse, nu ben ik in de war. Het KGV van 80,96,96 is idd geen 80*96, maar 480. Dus ik heb niet het KGV genomen? Ik dacht dat ik het goed had want dit kwam uit het antwoordenboekje:
Het 'probleem' is dat 8 en a-2 dezelfde factoren zijn. De vraag is of dat belangrijk is in dit geval, maar je zou dan dingen moeten uitsplitsen voor randgevallen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oh zo, ik snap waarom je dan a=10 nam, maar volgens mij is dit niet echt belangrijk voor deze som. Bij een andere a zou het wel goed uitkomen lijkt het mij....
Zij (|R, Borel, lesbegue maat) een measure space, f:|R->|R measurable zodat u(x,t):=exp(xt)f(x) Lesbegue-integreerbaar is voor iedere t in (a,b), waarbij a,b in |R zitten. Is de Lesbegue-integraal van u(x,t) over x in |R differentieerbaar voor iedere t in (a,b)?
Als het zo is, dan is het voldoende om aan te tonen dat u(x,t) differentieerbaar is naar t, lesbegue integreerbaar is over x in |R, en dat de afgeleide kleiner of gelijk is aan een lesbegue integreerbare functie q(x). De eerste twee dingen zijn duidelijk, maar in welke richting moet ik denken voor die q(x)?
Alvast bedankt.
Als het zo is, dan is het voldoende om aan te tonen dat u(x,t) differentieerbaar is naar t, lesbegue integreerbaar is over x in |R, en dat de afgeleide kleiner of gelijk is aan een lesbegue integreerbare functie q(x). De eerste twee dingen zijn duidelijk, maar in welke richting moet ik denken voor die q(x)?
Alvast bedankt.
Ik zit met een differentiatie waar ik niet uitkom. Het gaat om een combinatie van de kettingregel met de productregel:
En daar krijg ik (i.c.m. de kettingregel) de volgende afgeleide uit:
Nu is de afgeleide verder in orde, maar zodra ik het ga vereenvoudigen raak ik ergens -120X kwijt. Ik snap niet waar het zit, want ik heb echt alles geprobeerd... Het moet volgens mij antwoordenboek het volgende worden (en dit lijkt ook te kloppen):
En daar krijg ik (i.c.m. de kettingregel) de volgende afgeleide uit:
Nu is de afgeleide verder in orde, maar zodra ik het ga vereenvoudigen raak ik ergens -120X kwijt. Ik snap niet waar het zit, want ik heb echt alles geprobeerd... Het moet volgens mij antwoordenboek het volgende worden (en dit lijkt ook te kloppen):
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Mis jij hem ook bij de linkerhelft?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Ohh wacht te snel gerekend hij is wel goed.
(30-2x)^2 = 900 - 120x +4x^2
(x)(-4(30-2x) = -120x + 8x^2
(30-2x)^2 = 900 - 120x +4x^2
(x)(-4(30-2x) = -120x + 8x^2
Waar komt die eerste -120x vandaan? Ik zie namelijk alleen 900 (30^2) en 4x^2 (2x^2)quote:
Ohh wacht te snel gerekend hij is wel goed.
(30-2x)^2 = 900 - 120x +4x^2
(x)(-4(30-2x) = -120x + 8x^2
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
(30-2x)^2 = (30 - 2x) * (30 - 2x)quote:
[..]
Waar komt die eerste -120x vandaan? Ik zie namelijk alleen 900 (30^2) en 4x^2 (2x^2)
dus 30 * 30 = 900
30 * -2x = -60x
-2x * 30 = -60x
-2x * -2x = -4x^2
Het klopt toch echt. Het product van x, -4 en 30 in je tweede term is -120x. Overigens zou ik het niet zo opschrijven, je kunt beter niet de volgorde van de twee functies in je product omwisselen als je de afgeleide bepaalt, daarmee maak je het voor jezelf onnodig onoverzichtelijk. Verder is je gebruik van haakjes niet standaard, en dat komt de overzichtelijkheid ook niet ten goede.quote:
Ik zit met een differentiatie waar ik niet uitkom. Het gaat om een combinatie van de kettingregel met de productregel:
[ afbeelding ]
En daar krijg ik (i.c.m. de kettingregel) de volgende afgeleide uit:
[ afbeelding ]
Nu is de afgeleide verder in orde, maar zodra ik het ga vereenvoudigen raak ik ergens -120X kwijt. Ik snap niet waar het zit, want ik heb echt alles geprobeerd... Het moet volgens mij antwoordenboek het volgende worden (en dit lijkt ook te kloppen):
[ afbeelding ]
Ik besef nu (met dank aan voorgaande persoon) dat ik helemaal niet 30 keer -4 heb gedaan, maar alleen 30 keer 30 en 4 keer 4. Ik had dit kunnen weten.quote:
[..]
Het klopt toch echt. Het product van x, -4 en 30 in je tweede term is -120x. Overigens zou ik het niet zo opschrijven, je kunt beter niet de volgorde van de twee functies in je product omwisselen als je de afgeleide bepaalt, daarmee maak je het voor jezelf onnodig onoverzichtelijk. Verder is je gebruik van haakjes niet standaard, en dat komt de overzichtelijkheid ook niet ten goede.
Wat is er trouwens niet standaard aan de haakjes? Ik doe aan zelfstudie en sta open voor elke vorm van kritiek, aangezien ik dat amper krijg.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Haakjes dienen om volgordes van bewerkingen expliciet te maken resp. (zoals hier) om aan te geven dat twee of meer termen bij elkaar horen. Maar dan moet je dus niet (1) of (x) schrijven, daarbij is er namelijk maar één term tussen de haakjes en zijn de haakjes dus overbodig. Eventueel gebruik je een middenpunt (of bij gebrek daaraan een asterisk) om aan te geven dat er sprake is van een product, dus bijvoorbeeld x*-4*(30 - 2x).quote:
[..]
Ik besef nu (met dank aan voorgaande persoon) dat ik helemaal niet 30 keer -4 heb gedaan, maar alleen 30 keer 30 en 4 keer 4. Ik had dit kunnen weten.
Wat is er trouwens niet standaard aan de haakjes? Ik doe aan zelfstudie en sta open voor elke vorm van kritiek, aangezien ik dat amper krijg.
Oké op die manier. Bedankt voor het advies, ik zal het proberen te onthouden.quote:
[..]
Haakjes dienen om volgordes van bewerkingen expliciet te maken resp. (zoals hier) om aan te geven dat twee of meer termen bij elkaar horen. Maar dan moet je dus niet (1) of (x) schrijven, daarbij is er namelijk maar één term tussen de haakjes en zijn de haakjes dus overbodig. Eventueel gebruik je een middenpunt (of bij gebrek daaraan een asterisk) om aan te geven dat er sprake is van een product, dus bijvoorbeeld x*-4*(30 - 2x).
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Of nog netter is: -4x(30-2x). Als je eerst getallen schrijft en dan letters mag je het vermenigvuldigingsteken weglaten, maar dat wist je zo te zien alquote:
[..]
Oké op die manier. Bedankt voor het advies, ik zal het proberen te onthouden.
.
Stel ik wil x^3 x 2x + 2 opschrijven in factoren. Welke stappen zou ik dan kunnen nemen (het antwoord zou (x + 2)(x^2 2x + 1) moeten zijn.
Ik kan natuurlijk in dit in gedeelten oplossen:
x^3 + 2x + 2 = x(x^2-1) - 2(x-1) = x(x+1)(x-1) - 2(x-1)
Maar dan? Is het een kwestie van proberen?
[ Bericht 0% gewijzigd door Warren op 27-04-2011 14:19:53 ]
Ik kan natuurlijk in dit in gedeelten oplossen:
x^3 + 2x + 2 = x(x^2-1) - 2(x-1) = x(x+1)(x-1) - 2(x-1)
Maar dan? Is het een kwestie van proberen?
[ Bericht 0% gewijzigd door Warren op 27-04-2011 14:19:53 ]
Wat bedoel je met x^3 x 2x +2 en met (x+2)(x^2 2x +1)?quote:
Stel ik wil x^3 x 2x + 2 opschrijven in factoren. Welke stappen zou ik dan kunnen nemen (het antwoord zou (x + 2)(x^2 2x + 1) moeten zijn.
Ik kan natuurlijk in dit in gedeelten oplossen:
x^3 x 2x + 2 = x(x^2-1) - 2(x-1) = x(x+1)(x-1) - 2(x-1)
Maar dan? Is het een kwestie van proberen?
The biggest argument against democracy is a five minute discussion with the average voter.
Excuses.quote:
[..]
Wat bedoel je met x^3 x 2x +2 en met (x+2)(x^2 2x +1)?
Begin eens met dit te schrijven als:quote:
[..]
Excuses. [ afbeelding ] moet worden geschreven in factoren. Het antwoord zou moeten zijn [ afbeelding ]
x3 - 3x + 2
Je ziet nu vrij gemakkelijk door uitproberen dat x = -2 en x = 1 nulpunten zijn van deze veelterm, zodat deze dus deelbaar is door (x + 2) en door (x - 1). Voer dan een polynoomstaartdeling uit.
Ik moet van verschillende functies de extremen bepalen en het is de bedoeling dat ik dit uitreken. Echter weet ik niet of ik het nou echt moet uitrekenen, of dat het ook algebraïsch mag?
Stel dat ik een formule heb zoals: x^4 - 9x^2 hoe kan ik dan het beste de minimum/maximum vinden? Ik weet hoe het moet met de GRM, maar ik moet het dus ook kunnen berekenen?
Stel dat ik een formule heb zoals: x^4 - 9x^2 hoe kan ik dan het beste de minimum/maximum vinden? Ik weet hoe het moet met de GRM, maar ik moet het dus ook kunnen berekenen?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Je hebt net het concept van de afgeleide geleerd, dit is waar de afgeleide van pas komt. De afgeleide geeft immers de helling van de functie aan, als de helling nul is, is er dus een minimum of een maximum (strikt genomen kan er ook een buigpunt zijn, maar daar zal ik niet verder over uitweiden). Wat je dus moet doen is de afgeleide gelijk stellen aan nul, dat geeft je de x-coördinaat van het maximum/minimum, en daarmee kan je ook de y-coördinaat vinden (invullen in de oorspronkelijke formule).quote:
Ik moet van verschillende functies de extremen bepalen en het is de bedoeling dat ik dit uitreken. Echter weet ik niet of ik het nou echt moet uitrekenen, of dat het ook algebraïsch mag?
Stel dat ik een formule heb zoals: x^4 - 9x^2 hoe kan ik dan het beste de minimum/maximum vinden? Ik weet hoe het moet met de GRM, maar ik moet het dus ook kunnen berekenen?
The biggest argument against democracy is a five minute discussion with the average voter.
Ik weet dat de plek waar de afgeleide 0 is, zich een extreme bevindt, echter vraag ik mij af of ik het terug moet rekenen of dat ik het via één of andere magische methode op de waarde moet komen (behalve door de vergelijking algebraïsch uit elkaar te trekken met de uitkomst nul).quote:
[..]
Je hebt net het concept van de afgeleide geleerd, dit is waar de afgeleide van pas komt. De afgeleide geeft immers de helling van de functie aan, als de helling nul is, is er dus een minimum of een maximum (strikt genomen kan er ook een buigpunt zijn, maar daar zal ik niet verder over uitweiden). Wat je dus moet doen is de afgeleide gelijk stellen aan nul, dat geeft je de x-coördinaat van het maximum/minimum, en daarmee kan je ook de y-coördinaat vinden (invullen in de oorspronkelijke formule).
Even een aanvulling, om mijn vraag iets duidelijker te maken. Ik heb de volgende afgeleide en via vier stappen kom ik op de waarde van X als Y = 0. Nu is alleen de vraag of dit de juiste methode is en hoe ik ervoor zorg dat ik alle extremen vind. (In dit geval -2, 0 en 2)?
[ Bericht 16% gewijzigd door Pipo1234 op 28-04-2011 20:15:22 ]
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
dat klopt niet, f'(x) is geen 4x³. Daarnaast deel je ergens door x, wat als x=0?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Daar heb je inderdaad een goed punt... De methode werkte, maar ik wist even niet of het correct is.quote:
[ afbeelding ]
dat klopt niet, f'(x) is geen 4x³. Daarnaast deel je ergens door x, wat als x=0?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
een gevalletje abuse of notation dat slecht uitpakt dus....quote:
[ afbeelding ]
dat klopt niet, f'(x) is geen 4x³. Daarnaast deel je ergens door x, wat als x=0?
f '(x) = 4x³ - 18x
stel f '(x) = 0 => 4x³ - 18x = 0
x ( 4x2 - 18 ) = 0 =>
x = 0 OR 4x2 - 18 = 0
4x2 = 18
x2 = 4.5
x = SQRT(4.5) OR x = -SQRT(4.5)
4.5 = 9/2 = > SQRT(4.5) = SQRT(9/2) = 3/SQRT(2) = 3/2 * SQRT(2)
remember: SQRT(1/2) = 2-1/2 = 21/2 - 1 = SQRT(2) / 2
Het is de bedoeling dat ik de extremen van deze functie bepaal. Echter weet ik niet hoe ik bij de afgeleide de nulpunten moet bepalen, aangezien het niet om een gewone formule gaat. Kan iemand me even op weg helpen?
De afgeleide:
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |