[Bèta overig] Huiswerk- en vragentopic

Ik voel me nu heel stom in dit topic met bovenstaande vragen, maargoed. Ik moet een verslag schrijven voor natuurkunde, en nu zit de volgende vraag erin:

Wat zijn de frequentie en trillingstijd van een zuiver C?

Ik zou bij god niet weten hoe ik dit moet uitrekenen, het staat onder het kopje internetvragen maar een hoop gegoogel levert alleen een octavering met een heleboel verschillende frequenties op. Kan iemand me verder helpen?

Ik heb weer een vraag, ik moet een synthese van ijzersulfaat voorbereiden. Ijzer uit spijkers moet ik met behulp van zwavelzuur omzetten in ijzersulfaat.
Nu moet ik alle reactievergelijkingen die bij deze synthese voorkomen geven.
Ik heb deze:Fe + H2SO4 ---> FeSO4 +H2

Maar zouden er dan meer moeten zijn?

quote:

Op vrijdag 25 mei 2012 16:28 schreef daantje1044 het volgende:
Ik heb weer een vraag, ik moet een synthese van ijzersulfaat voorbereiden. Ijzer uit spijkers moet ik met behulp van zwavelzuur omzetten in ijzersulfaat.
Nu moet ik alle reactievergelijkingen die bij deze synthese voorkomen geven.
Ik heb deze:Fe + H2SO4 ---> FeSO4 +H2

Maar zouden er dan meer moeten zijn?

Het is fe2? Toch?

Hallo,

Mijn vraag, hieronder spreekt eigenlijk voor zich, kom niet uit de volgende vragen en ben er eigenlijk al de hele dag mee bezig, wellicht voor velen gesneden koek...

http://www.mijnbestand.nl/Bestand-3VP486ELFN6L.jpg
http://www.mijnbestand.nl/Bestand-BJNTMOA7HHOQ.jpg

Kan iemand mij op weg helpen richting de antwoorden? Ik weet niet wat ik moet vermenigvuldigen/delen etc...

mijn dank is groot!

Ok dank je wel, dan weet ik dat ik op de goede weg zit!

Ok, ik heb morgen een mondeling examen over 2 vragen waar ik de ballen niet van snap. Dus ik hoop dat jullie het wat beter kunnen uitleggen. Ik moet een systeem met 2 lijnen "oplossen" (dus uitrekenen waar die 2 lijnen kruizen)

de ene keer moet ik deze echt uitrekenen, en met een 2e set moet ik dit grafisch doen.

Diegene die ik moet uitrekenen gaat als volgt :

{
{

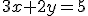
Je moet die oplossen met de "plus" methode ofzo. Maar ik snap niet hoe die werkt

De 2e die je grafisch moet oplossen ziet er zo uit:




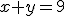
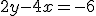
Een beetje een grote vraag maar ik hoop dat iemand het uit wil leggen

Ik weet dat dit het bèta topic is, maar het is "de ballen ergens van begrijpen" ipv "de ballen ergens niet van snappen".

Meh, oplossen met de plus-methode ... klinkt als de zoveelste pikkepoelie-onzin rechtstreeks uit de koker van de PABO-mutsjes die zich door kinders van groep 8 eruit laten staartdelen

Beter hanteer je simpele elementaire algebraïsche technieken voor 2 vergelijkingen met 2 onbekenden. Het principe berust op het feit dat je 1 variabele als functie van de ander schijft en die functie dan in de andere vergelijking voor de eerste variabele inplugt. Met de eerste opgave als voorbeeld krijgen we:

2x - y = 8 ^ 3x + 2y =5
^ _{Staat nu niet voor machtsverheffen maar voor de logische EN}

We kunnen dus ook direct schrijven 2x - 8 = y ^ 3x + 2y =5

en dus kunnen we direct 2x - 8 voor y inpluggen in 3x + 2y = 5
wat ons 3x + 4x - 16 = 5 oplevert

verder oplossen geeft:
7x - 16 = 5
7x - 21 = 0
7x = 21
x=3

plug nu in de eerste vgl 2x - y = 8 de waarde 3 die je zojuist hebt gevonden voor x:
2*3 - y = 8
6 -y = 8
-y = 2
y = -2


Voor de tweede opgave die grafisch (hoe verzinnen ze het ) opgelost dient te worden moet je beide leden van het stelsel van vergelijkingen omschrijven naar de algemene versie v/d lineaire vergelijking ax + b = y . Here goes.

x+y = 9 => x + y - 9 = 0 => x - 9 = -y => 9 - x = y
2y - 4x = -6 => 2y = -6 + 4x => 2y = 4x - 6 => y = 2x - 3

Als je deze lineaire vgl's in een cartestisch coördinatenstelsel tekent is direct het snijpunt (en géén, ik herhaal, géén kruispunt) zichbaar. Maar een beetje maths geek prefereert altijd een analytische oplossing.

x+y=9 => y = 9-x
2y-4x = -6 ^ y = 9-x => 2*(9-x) - 4x = -6 => 18-2x-4x = -6 => 18-6x = -6 => 3-x=1 => 4-x=0 => x=4

x+y=9 ^ x=4 => 4+y=9 => y=5

Het snijpunt is dus (4,5)

EDIT: fout verbeterd.

[ Bericht 14% gewijzigd door VanishedEntity op 28-05-2012 21:48:40 ]

_dubbelpost

quote:

Op maandag 28 mei 2012 21:19 schreef VanishedEntity het volgende:
Meh, oplossen met de plus-methode ... klinkt als de zoveelste pikkepoelie-onzin rechtstreeks uit de koker van de PABO-mutsjes die zich door kinders van groep 8 eruit laten staartdelen

Beter hanteer je simpele elementaire algebraïsche technieken voor 2 vergelijkingen met 2 onbekenden. Het principe berust op het feit dat je 1 variabele als functie van de ander schijft en die functie dan in de andere vergelijking voor de eerste variabele inplugt. Met de eerste opgave als voorbeeld krijgen we:

2x - y = 8 ^ 3x + 2y =5
^ _{Staat nu niet voor machtsverheffen maar voor de logische EN}

We kunnen dus ook direct schrijven 2x - 8 = y ^ 3x + 2y =5

en dus kunnen we direct 2x - 8 voor y inpluggen in 3x + 2y = 5
wat ons 3x + 4x - 16 = 5 oplevert

verder oplossen geeft:
7x - 16 = 5
7x - 21 = 0
7x = 21
x=3

plug nu in de eerste vgl 2x - y = 8 de waarde 3 die je zojuist hebt gevonden voor x:
2*3 - y = 8
6 -y = 8
-y = 2
y = -2

Voor de tweede opgave die grafisch (hoe verzinnen ze het ) opgelost dient te worden moet je beide leden van het stelsel van vergelijkingen omschrijven naar de algemene versie v/d lineaire vergelijking ax + b = y . Here goes.

x+y = 9 => x + y - 9 = 0 => x - 9 = -y => 9 - x = y
2y - 4x = -6 => 2y = -6 + 4x => 2y = 4x - 6 => y = 2x - 3

Als je deze lineaire vgl's in een cartestisch coördinatenstelsel tekent is direct het snijpunt (en géén, ik herhaal, géén kruispunt) zichbaar. Maar een beetje maths geek prefereert altijd een analytische oplossing.

x+y=9 => y = 9-x
2y-4x = -6 ^ y = 9-x => 2*(9-x) - 4x = -6 => 18-2x-4x = -6 => 18-6x = -6 => 3-x=1 => 2-x=0 => x=2

x+y=9 ^ x=2 => 2+y=9 => y=7

Het snijpunt is dus (2,7)

ok, ik begin even bij de 2e omdat die me het makkelijkste lijkt. Echter, weet je zeker dat dat goed zit?

Kan je die eerste niet omschrijven van

x+y=9 naar y= -x+9 ? wat je dus een lijn geeft die bij y= +9 de y kruist?

Wat je dus een kruisingspunt van x = 4 en Y = 5 geeft?

Kan het mis hebben hoor. Ik snap het nog maar half.

quote:

Op maandag 28 mei 2012 21:36 schreef gogosweden het volgende:

[..]

ok, ik begin even bij de 2e omdat die me het makkelijkste lijkt. Echter, weet je zeker dat dat goed zit?

Kan je die eerste niet omschrijven van

x+y=9 naar y= -x+9 ? wat je dus een lijn geeft die bij y= +9 de y kruist?

Wat je dus een kruisingspunt van x = 4 en Y = 5 geeft?

Kan het mis hebben hoor. Ik snap het nog maar half.

Ik zit zelf ook al te kijken waar de fout zit, maargoed, de gehanteerde techniek en principes blijven staan. ff wachten, pak pen en papier erbij.

EDIT: fout gevonden; het moet zijn 18-6x = -6 => 3-x = -1 => 4-x = 0 => 4=x
wat dus daarna x+y=9 ^ x=4 => 4+y=9 => y=5 oplevert. Je had eerder dan mij de correcte coördinaten van het snijpunt (engels: point of intersection) gevonden dus je bent al goed op weg om het te snappen. En idd, y = 9-x is idd hetzelfde als y = -x + 9.

[ Bericht 0% gewijzigd door VanishedEntity op 28-05-2012 21:53:13 ]

Just throw us another one als je iets nog niet snapt.

quote:

Op maandag 28 mei 2012 22:06 schreef VanishedEntity het volgende:
Just throw us another one als je iets nog niet snapt.

ja is goed ik ben het nu even allemaal aan het doornemen. Ik hoef alleen maar uit te leggen hoe ik tot het antwoord gekomen ben, dus eigenlijk valt het redelijk mee als ik deze gewoon in mijn kop ram. Maar het is natuurlijk nooit verkeerd om het goed te leren zoals nu.

Enorm bedankt voor je hulp! en mocht ik nog een probleem hebben laat ik van me horen

quote:

Op zondag 13 mei 2012 13:53 schreef datisstom het volgende:
Ik voel me nu heel stom in dit topic met bovenstaande vragen, maargoed. Ik moet een verslag schrijven voor natuurkunde, en nu zit de volgende vraag erin:

Wat zijn de frequentie en trillingstijd van een zuiver C?

Ik zou bij god niet weten hoe ik dit moet uitrekenen, het staat onder het kopje internetvragen maar een hoop gegoogel levert alleen een octavering met een heleboel verschillende frequenties op. Kan iemand me verder helpen?

Frequentie van zuivere noten staan in de Binas, tabel 15 geloof ik. Met 'frequentie = 1/trillingstijd' kun je dan de trillingstijd bepalen. (staat ook in B-35)

quote:

Op maandag 28 mei 2012 21:06 schreef gogosweden het volgende:
Ok, ik heb morgen een mondeling examen over 2 vragen waar ik de ballen niet van snap. Dus ik hoop dat jullie het wat beter kunnen uitleggen. Ik moet een systeem met 2 lijnen "oplossen" (dus uitrekenen waar die 2 lijnen kruizen)

de ene keer moet ik deze echt uitrekenen, en met een 2e set moet ik dit grafisch doen.

Diegene die ik moet uitrekenen gaat als volgt :

{
{

Je moet die oplossen met de "plus" methode ofzo. Maar ik snap niet hoe die werkt

De 2e die je grafisch moet oplossen ziet er zo uit:




Een beetje een grote vraag maar ik hoop dat iemand het uit wil leggen

De plusmethode is zeker dat je ze bij elkaar optelt en dat er dan wat tegen elkaar weg valt. Je kan het stelsel schrijven als

4x - 2y = 16
3x + 2y = 5

De linker en rechterkanten bij elkaar optellen geeft

7x = 21
x = 3

Vervolgens kan je x=3 invullen in (1) of in (2) om y te berekenen.

Gaat een stuk sneller.

Voor de tweede, schrijf het stelsel als:
4x + 4y = 36
-4x + 2y = -6
---------------------+
6y=30

Dus y=5. En dan weer invullen om x te berekenen.

"Gaat een stuk sneller" heb je alleen nog niet heel veel aan als je niet helemaal door hebt welke stappen je dient te maken, dus vandaar de nogal uitgeweide versie. Bovendien, die plus-methode kan je meteen van tafel gooien zodra er kwadraten en hogere machten en/of er meer vergelijkingen en onbekenden aan te pas komen; substituties zijn wdb meer fool-proof.

Ook bij grotere lineaire stelsels werkt die methode (zegt Gaussische eliminatie je iets?).

De basis statica is een beetje weggezakt. Dus hoe ging dit ook alweer?

Gegeven een goal (voetbal). Kracht van 1000 N precies op het midden naar beneden (-1000N dus). Doel is 7,32 m breed en 2,44 m hoog. De goal staat dus vast aan de grond.



Gevraagd: Reactiekrachten en moment om Z in A.

Fy = 500N (logisch)

Nu geeft ANSYS aan voor Fx = -481 N en Mz = 391.78 Nm.

Nu kom ik zelf op een veel groter moment uit, mijn FBD methode mist nog iets.

Weet een van jullie dat hier?

Hellllppp, mijn wereld staat op de kop.
Vroeger op de basisschool had je weleens vragen als:

quote:

Een gevuld bad loopt leeg in 8 minuten. De linker kraan vult het bad in 12 minuten en de rechter kraan vult het bad in 6 minuten. Als de stop eruit is hoelang duurt het als beide kranen open staan om het bad te vullen?

Antwoord: in 8 minuten

Nu krijg ik de vraag:

quote:

Een rechthoekige badkuip heeft een constante doorsnede over de hoogte. Als de kraan wijd open staat en de afvoer gesloten is, stroomt het bad in 20 minuten vol. De waterhoogte is dan 50 cm. Het tot deze hoogte gevulde bad loopt bij gesloten kraan leeg in 32 min, via afvoer in de bodem. Hoe hoog zal het water in het bad staan als zowel kraan als afvoer open staan?

Antwoord: 32 cm

Kan iemand mij dit uitleggen? (En dan vooral waarom ik er bij bovenstaande vraag vanuit mag gaan dat de hoogte constant blijft, zoals in het antwoord wordt aangenomen.)

Correctie, dat stroom in = stroom uit.

[ Bericht 2% gewijzigd door Ofresca op 30-05-2012 14:55:18 ]

quote:

Op woensdag 30 mei 2012 14:41 schreef Ofresca het volgende:
Hellllppp, mijn wereld staat op de kop.
Vroeger op de basisschool had je weleens vragen als:

[..]

Nu krijg ik de vraag:

[..]

Kan iemand mij dit uitleggen? (En dan vooral waarom ik er bij bovenstaande vraag vanuit mag gaan dat de hoogte constant blijft, zoals in het antwoord wordt aangenomen.)

Correctie, dat stroom in = stroom uit.

Omdat, als niet geldt stroom in = stroom uit, het waterpeil nog 'aan het veranderen' is (en dus niet constant). Als er meer water bijkomt dan er uitstroomt, zal het waterpeil stijgen en omgekeerd.

Ze hebben het in de vraag inderdaad niet genoemd, maar ze willen dus eigenlijk de hoogte weten waar het water 'naar toe gaat'. De evenwichtstoestand, als het ware (God wat ben ik slecht in dit soort dingen formuleren )

quote:

Op woensdag 30 mei 2012 15:23 schreef kutkloon7 het volgende:

[..]

Omdat, als niet geldt stroom in = stroom uit, het waterpeil nog 'aan het veranderen' is (en dus niet constant). Als er meer water bijkomt dan er uitstroomt, zal het waterpeil stijgen en omgekeerd.

Ze hebben het in de vraag inderdaad niet genoemd, maar ze willen dus eigenlijk de hoogte weten waar het water 'naar toe gaat'. De evenwichtstoestand, als het ware (God wat ben ik slecht in dit soort dingen formuleren )

Maar waarom mag ik er vanuit gaan dat die er is? Stel nou dat het bad wel zou overstromen, dan zou hoogte zeker (er valt een kwartje) > 50 cm zijn?

quote:

Op woensdag 30 mei 2012 15:29 schreef Ofresca het volgende:

[..]

Maar waarom mag ik er vanuit gaan dat die er is? Stel nou dat het bad wel zou overstromen, dan zou hoogte zeker (er valt een kwartje) > 50 cm zijn?

Ja, en als ie leeg zou lopen zou er een negatieve hoogte uit komen.

Volgens mij moet je er trouwens van uitgaan dat de uitstroomsnelheid evenredig is met de hoeveelheid water, dan kan je een differentiaalvergelijking opstellen.

quote:

Op woensdag 30 mei 2012 15:29 schreef Ofresca het volgende:

[..]

Maar waarom mag ik er vanuit gaan dat die er is? Stel nou dat het bad wel zou overstromen, dan zou hoogte zeker (er valt een kwartje) > 50 cm zijn?

Het water stijgt niet meer als de uitstroom via de afvoer gelijk is aan de instroom vanuit de kraan. Kennelijk is het de bedoeling dat je aanneemt dat de uitstroomsnelheid evenredig is met de hoogte van het water in het bad, zodat de uitstroomsnelheid dus toeneemt naarmate het bad zich vult. Maar dan nog is de opgave niet op te lossen met de gegevens die je hebt gekregen.

Stel t drukt de tijd uit in minuten, en h(t) is de hoogte van de waterstand in het bad in cm op tijdstip t. De instroom vanuit de kraan is constant, en aangezien in 20 minuten het bad is gevuld en de hoogte van de waterstand dan 50 cm bedraagt, komt er 2,5 cm water per minuut bij, zodat voor het vullen van het bad met gesloten afvoer dus geldt h(t) = 2,5∙t, en dus h'(t) = 2,5. Voor het laten leeglopen van het bad (kraan dicht) geldt dat h'(t) negatief is, en evenredig met h(t), dus h'(t) = -c∙h(t). Aangezien we beginnen met een leeg bad, dus h(0) = 0, krijgen we dan voor de combinatie van het laten vullen van het bad en het laten wegstromen van het water via de afvoer de volgende differentiaalvergelijking:

h'(t) = 2.5 - c∙h(t), h(0) = 0

De oplossing van deze DV is:

h(t) = (2,5 - 2,5∙e^-ct)/c

Het badwater kan dus niet hoger stijgen dan tot een hoogte 2,5/c. Alleen zie ik niet hoe je met de gegevens uit de opgave c zou moeten bepalen.

[ Bericht 0% gewijzigd door Riparius op 30-05-2012 17:07:32 ]