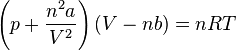[Bèta wiskunde] Huiswerk-en-vragentopic

y moet je integreren over het interval van y waarop f(x,y) positief is?

Denk dat dat hem is

quote:

Op zaterdag 20 november 2010 14:29 schreef GlowMouse het volgende:
Wat je nu doet is P(2X < Y) = P(X < y/2), maar het is P(2X < Y) = E_Y(P_X(X < y/2)). F_X(x) te berekenen is teveel werk voor deze opgave, want daarna moet je ook nog over alle mogelijke waarden van Y itereren om die verwachting te bepalen.

Het is gewoon hetzelfde, maar hier zie je het antwoord makkelijker door direct een dubbelintegraal op te stellen.

Volgens mij geldt de formule P(2X < Y) = E_Y(P_X(X < y/2)) alleen als X en Y onafhankelijk zijn? Als bijv. X=Y/2, dan is P(2 X<Y)=0, maar dat geldt niet noodzakelijkerwijs voor E_Y(P_X(X < y/2)), in het algemeen moet je in de verwachting conditioneren op de waarde van Y?

[ Bericht 3% gewijzigd door keesjeislief op 20-11-2010 15:16:46 ]

quote:

Op zaterdag 20 november 2010 14:51 schreef BasementDweller het volgende:
y moet je integreren over het interval van y waarop f(x,y) positief is?

Denk dat dat hem is

Als je de methode in mijn post gebruikt, zie je vanzelf waarover je precies moet integreren.

quote:

Op zaterdag 20 november 2010 15:01 schreef keesjeislief het volgende:

[..]



Als je de methode in mijn post gebruikt, zie je vanzelf waarover je precies moet integreren.

Heb ik gedaan

Omdat 0=<x=<1 en 0=<y=<2:

x over [0,y/2] en y over [0,2]

of

y over [2x,2] en x over [0,1]

quote:

Op zaterdag 20 november 2010 15:37 schreef BasementDweller het volgende:

[..]


Heb ik gedaan

Omdat 0=<x=<1 en 0=<y=<2:

x over [0,y/2] en y over [0,2]

of

y over [2x,2] en x over [0,1]

.

quote:

Op vrijdag 19 november 2010 17:27 schreef Riparius het volgende:

[..]



Je had onmiddellijk kunnen concluderen dat je antwoord fout was, zelfs al wist je niet hoe het dan wel moest. Immers, als f'(x) een lineaire functie van x is, dan moet je f(x) een kwadratische functie van x zijn, maar dat is niet zo: een tegenspraak. Kun je overigens verklaren waarom je dacht dat de kettingregel niet gold voor de logaritmische functie? Ik ben altijd geïnteresseerd in dat soort kromme argumenten, omdat het iets bloot kan leggen over didactische tekortkomingen.

Nooit echt duidelijk uitgelegd wanneer te gebruiken

quote:

Op zaterdag 20 november 2010 17:07 schreef Granaatappel het volgende:

[..]



Nooit echt duidelijk uitgelegd wanneer te gebruiken

Is dat nu wel duidelijk?

Je gebruikt de kettingregel als je een samengestelde functie hebt. Dus je hebt een functie f(x) maar je kan die ook schrijven als g(h(x)). Bij ln(1/x) kan je zeggen h(x)=1/x en g(h(x))=ln(1/x).

Dan geldt f'(x) = g'(h(x)) h'(x) volgens de kettingregel.

quote:

Op zaterdag 20 november 2010 19:53 schreef BasementDweller het volgende:

[..]


Is dat nu wel duidelijk?

Je gebruikt de kettingregel als je een samengestelde functie hebt. Dus je hebt een functie f(x) maar je kan die ook schrijven als g(h(x)). Bij ln(1/x) kan je zeggen h(x)=1/x en g(h(x))=ln(1/x).

Dan geldt f'(x) = g'(h(x)) h'(x) volgens de kettingregel.

Jep bedankt.
Er worden bij ons vaak standaardfuncties gebruikt als ln(x) of e^x en dan leer je meteen het simpelste voorbeeld dus was even lastig uit te vogelen hoe het precies werkt maar ik snap het nu bedankt.

kettingregel was zelfs helemaal niet nodig, ln(1/x) is gewoon hetzelfde als -lnx, en dan wordt het eenvoudig. Vandaar dat het mss nog bij de eenvoudige oefeningen stond.

Ik zit een beetje met deze opgave, ik kom er niet uit omdat ik eigenlijk niet begrijp hoe impliciet differentiëren werkt.

Ik moet hier dV/dP vinden, en ik kan aannemen dat T constant blijft (Dit is dus de Van der Waals vergelijking)

Verder heb ik dus hetzelfde probleem met deze opdracht:

Dit is een ellips en ik moet dmv impliciet differentieren vinden dat de tangent op punt (x0,y0) gelijk is aan


Ik heb bij beiden een mooie knoeboel in m'n schrift dus dat ga ik maar niet opschrijven, kan iemand mij dus een stukje op weg helpen?

Ik kan wel op het antwoord van die tweede komen, maar ik knoei maar wat aan zeg ik er eerlijk bij, kan vast veel eleganter. Hoe dan ook, wat je kunt doen is eerst zeggen dat een raaklijn (tangent) van de vorm A x + B y = 1 is. (Dit is gewoon de gebruikelijke y=.. x + .. in herschreven vorm). Neem een (x_0,y_0) op de originele kromme. De raaklijn moet nu door het punt (x_0,y_0) gaan, d.w.z. er moet gelden

A x_0 + B y_0 = 1 (*)

en de raaklijn moet raken aan de originele kromme in dat punt, d.w.z. er moet gelden dat de dy/dx voor beide krommen overeen komen als je ze in het punt (x_0,y_0) beschouwt. Impliciet differentieren van de originele kromme geeft 2 x/a^2 + 2 y (dy/dx) /b^2 = 0, en dus in het punt (x_0,y_0):

2 x_0/a^2 + 2 y_0 (dy/dx)|_{(x,y)=(x_0,y_0)} /b^2 = 0 (**)

Idem voor de raaklijn, impliciet differentieren geeft A + B (dy/dx) = 0, en dus:

A + B (dy/dx)|_{(x,y)=(x_0,y_0)} = 0 (***).

Nu moet je het probleem van het vinden van de A en B oplossen door te zorgen dat de (dy/dx)|_{(x,y)=(x_0,y_0)} uit (**) gelijk is aan de (dy/dx)|_{(x,y)=(x_0,y_0)} uit (***), terwijl ook (*) moet gelden. Als je dit uitwerkt, of even goed naar de vergelijkingen staart, dan zie je dat je inderdaad krijgt A = x_0/a^2 en B = y_0/b^2.

quote:

Gegeven zijn de functies f(x)= 2*sin(x) en g(x)=2*cos(x)
Onderzoek algebraïsch of de grafieken van f en g elkaar loodrecht snijden.

Volgens het boek is de regel dan dat je moet nagaan of f(x)=g(x) en f '(x)*g '(x)=-1 beide ergens gelden.
Ik krijg dan voor f(x)=g(x) 2*sin(x)=2*cos(x) dus sin(x)=cos(x)
en voor f '(x)*g '(x)=-1 krijg ik
(2*cos(x))*(2*-sin(x))=-1 -> 2-2*sin(x)+2*cos(x)-cos(x)*sin(x)=-1

Ik kwam hier niet zo snel uit, dus ik keek even naar de uitwerkingen van het boek, en wat schetste mijn verbazing:
voor f '(x)*g'(x)=-1 staat er 2*cos(x)*2*-sin(x) = -1
Zonder de haakjes, gewoon achter elkaar geplakt..

Klopt dit echt? Ik zou toch denken dat als de regel is f '(x) * g'(x) = -1, je die gehele functies * elkaar moet doen dus ze tussen haakjes zou moeten zetten?

Edit: Worteltekens doen het hier blijkbaar niet.. Overal waar 2*iets staat, moet het wortel2*iets staan

quote:

Op zondag 21 november 2010 14:21 schreef Thas het volgende:

[..]

Volgens het boek is de regel dan dat je moet nagaan of f(x)=g(x) en f '(x)*g '(x)=-1 beide ergens gelden.
Ik krijg dan voor f(x)=g(x) 2*sin(x)=2*cos(x) dus sin(x)=cos(x)
en voor f '(x)*g '(x)=-1 krijg ik
(2*cos(x))*(2*-sin(x))=-1 -> 2-2*sin(x)+2*cos(x)-cos(x)*sin(x)=-1

Ik kwam hier niet zo snel uit, dus ik keek even naar de uitwerkingen van het boek, en wat schetste mijn verbazing:
voor f '(x)*g'(x)=-1 staat er 2*cos(x)*2*-sin(x) = -1
Zonder de haakjes, gewoon achter elkaar geplakt..

Klopt dit echt? Ik zou toch denken dat als de regel is f '(x) * g'(x) = -1, je die gehele functies * elkaar moet doen dus ze tussen haakjes zou moeten zetten?

Deze stap:

(2*cos(x))*(2*-sin(x))=-1 -> 2-2*sin(x)+2*cos(x)-cos(x)*sin(x)=-1

klopt inderdaad niet, je maakt jezelf in de war met dat minteken denk ik, het is gewoon 2*cos(x)*2*-sin(x) = -4*sin(x)*cos(x).

quote:

Op zondag 21 november 2010 14:24 schreef keesjeislief het volgende:

[..]



Deze stap:

(2*cos(x))*(2*-sin(x))=-1 -> 2-2*sin(x)+2*cos(x)-cos(x)*sin(x)=-1

klopt inderdaad niet, je maakt jezelf in de war met dat minteken denk ik, het is gewoon 2*cos(x)*2*-sin(x) = -4*sin(x)*cos(x).

Worteltekens doen het hier blijkbaar niet.. Overal waar 2*iets staat, moet het wortel2*iets staan, sorry

quote:

Op zondag 21 november 2010 14:25 schreef Thas het volgende:

[..]



Worteltekens doen het hier blijkbaar niet.. Overal waar 2*iets staat, moet het wortel2*iets staan, sorry

Geen probleem, bedoel je nu dan sqrt(2)*sin(x) of sqrt(2*sin(x))? In het eerste geval geldt mijn opmerking nog steeds, met de 2 vervangen door sqrt(2).

Edit: met de code & #8730; (zonder spatie) krijg je een wortelteken: √.

quote:

Op zondag 21 november 2010 14:26 schreef keesjeislief het volgende:

[..]



Geen probleem, bedoel je nu dan sqrt(2)*sin(x) of sqrt(2*sin(x))? In het eerste geval geldt mijn opmerking nog steeds, met de 2 vervangen door sqrt(2).

EDit: werkt √?

Ah, als √ werkt het dus wel, bedankt
Ik bedoelde inderdaad het eerste, maar ik zie het nu inderdaad denk ik, bedankt

quote:

Op zondag 21 november 2010 14:30 schreef Thas het volgende:

[..]



Ah, als √ werkt het dus wel, bedankt
Ik bedoelde inderdaad het eerste, maar ik zie het nu inderdaad denk ik, bedankt

Ok. _{Als je vast komt te zitten met het oplossen van die twee vergelijkingen, gebruik die eerste vergelijking een beetje slim om in die tweede vergelijking alleen een sin (of alleen een cos) over te houden.}.

quote:

Op zondag 21 november 2010 14:26 schreef keesjeislief het volgende:

Edit: met de code & #8730; (zonder spatie) krijg je een wortelteken: √.

Waar heb je een overzichtje met al die codes, of weet je ze uit je hoofd?

quote:

Op zondag 21 november 2010 12:47 schreef Fingon het volgende:
Ik zit een beetje met deze opgave, ik kom er niet uit omdat ik eigenlijk niet begrijp hoe impliciet differentiëren werkt.
[ afbeelding ]
Ik moet hier dV/dP vinden, en ik kan aannemen dat T constant blijft (Dit is dus de Van der Waals vergelijking)

Verder heb ik dus hetzelfde probleem met deze opdracht:
[ afbeelding ]
Dit is een ellips en ik moet dmv impliciet differentieren vinden dat de tangent op punt (x0,y0) gelijk is aan
[ afbeelding ]

Ik heb bij beiden een mooie knoeboel in m'n schrift dus dat ga ik maar niet opschrijven, kan iemand mij dus een stukje op weg helpen?

Om ook nog even terug te komen op je eerste vraag over impliciet differentieren. In principe is impliciet differentieren niet zo anders dan 'gewoon' differentieren. Je kent het principe: een functie f(x)=x^2+6 wordt na differentieren: f'(x)=2 x. We kunnen dit ook op een iets andere manier opschrijven, te beginnen met de functie te zien als een vergelijking: y=x^2+6. Immers een functie beeldt een origineel (variabele x) af op het beeld (variabele y), en dat kan op verschillende manieren opgeschreven worden: f(x)=x^2+6; x -> x^2+6 of y=x^2+6. Alledrie betekenen ze eigenlijk hetzelfde, met dit verschil dat de notatie y=x^2+6 duidelijk maakt dat je kijkt naar een verzameling punten in R^2 namelijk die punten (x,y) waarvoor de relatie y=x^2+6 geldt. Als je deze verzameling punten zou 'tekenen' in een assenstelsel, krijg je (natuurlijk) hetzelfde als wanneer je de grafiek van f zou plotten.

Goed, nu is impliciet differentieren niet veel meer dan een vergelijking nemen en differentieren naar een van de variabelen. Stel we differentieren de vergelijking y=x^2+6 naar x (anders gezegd: we laten de operator d/dx los op beide kanten van de vergelijking). Dan krijgen we de vergelijking dy/dx=2 x. Waarom? Nou, aan de linkerkant hadden we een y. Dit is een variabele die van x afhangt en het symbool dy/dx betekent niets anders dan "y gedifferentieerd naar x". Aan de rechterkant hebben we x^2, dat levert bij differentieren naar x de gebruikelijke 2 x op, en 6 verdwijnt bij differentieren naar x zoals gebruikelijk.

Nog een voorbeeld. Laten we alle punten op de eenheidscirkel nemen. Die worden gegeven door de vergelijking x^2+y^2=1. Laten we nu impliciet differentieren naar x, dit geeft 2 x + 2 y (dy/dx)=0. De y^2 wordt na differentieren een 2 y (dy/dx) door de kettingregel. Als iemand je vraagt de afgeleide van de functie g(x)=f(x)^2 te berekenen, dan kom je via de kettingregel op 2 f(x) f'(x), hierboven volg je hetzelfde principe door te bedenken dat y eigenlijk een functie/afhankelijk is van x. We krijgen dus 2 x + 2 y (dy/dx) =0, oftewel dy/dx = -x/y. Inderdaad, als je even snel een eenheidscirkeltje tekent, er een punt (x_0,y_0) op kiest en de helling van de raaklijn in dat punt bekijkt, dan zul je vinden dat die helling gelijk is aan -x_0/y_0. Neem bijvoorbeeld het punt (0,1), daar is de helling 0 en dat klopt met de formule. Een ander voorbeeld is het punt (1,0). Als je dat invult, kom je op -1/0, dus de afgeleide bestaat niet/is ongedefinieerd. Inderdaad, de raaklijn in dat punt is een verticale lijn, een helling van oneindig zou je kunnen zeggen.

Helpt dit?

quote:

Op zondag 21 november 2010 15:07 schreef BasementDweller het volgende:

[..]


Waar heb je een overzichtje met al die codes, of weet je ze uit je hoofd?

Glowmouse en Riparius wel denk ik, ik gewone sterveling gebruik bijv. dit overzichtje: http://tntluoma.com/sidebars/codes/. .

Dankje

quote:

Op zondag 21 november 2010 15:12 schreef keesjeislief het volgende:

[..]



Om ook nog even terug te komen op je eerste vraag over impliciet differentieren. In principe is impliciet differentieren niet zo anders dan 'gewoon' differentieren. Je kent het principe: een functie f(x)=x^2+6 wordt na differentieren: f'(x)=2 x. We kunnen dit ook op een iets andere manier opschrijven, te beginnen met de functie te zien als een vergelijking: y=x^2+6. Immers een functie beeldt een origineel (variabele x) af op het beeld (variabele y), en dat kan op verschillende manieren opgeschreven worden: f(x)=x^2+6; x -> x^2+6 of y=x^2+6. Alledrie betekenen ze eigenlijk hetzelfde, met dit verschil dat de notatie y=x^2+6 duidelijk maakt dat je kijkt naar een verzameling punten in R^2 namelijk die punten (x,y) waarvoor de relatie y=x^2+6 geldt. Als je deze verzameling punten zou 'tekenen' in een assenstelsel, krijg je (natuurlijk) hetzelfde als wanneer je de grafiek van f zou plotten.

Goed, nu is impliciet differentieren niet veel meer dan een vergelijking nemen en differentieren naar een van de variabelen. Stel we differentieren de vergelijking y=x^2+6 naar x (anders gezegd: we laten de operator d/dx los op beide kanten van de vergelijking). Dan krijgen we de vergelijking dy/dx=2 x. Waarom? Nou, aan de linkerkant hadden we een y. Dit is een variabele die van x afhangt en het symbool dy/dx betekent niets anders dan "y gedifferentieerd naar x". Aan de rechterkant hebben we x^2, dat levert bij differentieren naar x de gebruikelijke 2 x op, en 6 verdwijnt bij differentieren naar x zoals gebruikelijk.

Nog een voorbeeld. Laten we alle punten op de eenheidscirkel nemen. Die worden gegeven door de vergelijking x^2+y^2=1. Laten we nu impliciet differentieren naar x, dit geeft 2 x + 2 y (dy/dx)=0. De y^2 wordt na differentieren een 2 y (dy/dx) door de kettingregel. Als iemand je vraagt de afgeleide van de functie g(x)=f(x)^2 te berekenen, dan kom je via de kettingregel op 2 f(x) f'(x), hierboven volg je hetzelfde principe door te bedenken dat y eigenlijk een functie/afhankelijk is van x. We krijgen dus 2 x + 2 y (dy/dx) =0, oftewel dy/dx = -x/y. Inderdaad, als je even snel een eenheidscirkeltje tekent, er een punt (x_0,y_0) op kiest en de helling van de raaklijn in dat punt bekijkt, dan zul je vinden dat die helling gelijk is aan -x_0/y_0. Neem bijvoorbeeld het punt (0,1), daar is de helling 0 en dat klopt met de formule. Een ander voorbeeld is het punt (1,0). Als je dat invult, kom je op -1/0, dus de afgeleide bestaat niet/is ongedefinieerd. Inderdaad, de raaklijn in dat punt is een verticale lijn, een helling van oneindig zou je kunnen zeggen.

Helpt dit?

Mja het lukt me op zich ook nog wel maar met gecompliceerde functies krijg ik dan gedoe, voornamelijk dat dy/dx gedoe dan.

quote:

2 x + 2 y (dy/dx) =0, oftewel dy/dx = -x/y

Dat dy/dx=-x/y , dat gaat alleen in dit geval op omdat het zo'n mooie functie is of gaat dat ook op voor de functies in die opgaven die ik moet maken en hoef ik ze dan alleen om te schrijven naar x =... en y = .... en dat vervolgens invullen in -(x)/y ?

quote:

Op zondag 21 november 2010 15:46 schreef Fingon het volgende:

[..]


Mja het lukt me op zich ook nog wel maar met gecompliceerde functies krijg ik dan gedoe, voornamelijk dat dy/dx gedoe dan.

[..]

Dat dy/dx=-x/y , dat gaat alleen in dit geval op omdat het zo'n mooie functie is of gaat dat ook op voor de functies in die opgaven die ik moet maken en hoef ik ze dan alleen om te schrijven naar x =... en y = .... en dat vervolgens invullen in -(x)/y ?

Dat dy/dx =-x/y volgt uit 2 x + 2 y (dy/dx) =0, dat geldt inderdaad (natuurlijk) alleen in dit specifieke geval. Als je bijv. zou hebben 4 x + 6 y^3 = 5 krijg je dy/dx = -4/(18 y^2), kun je dat zelf narekenen?