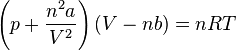[Bèta wiskunde] Huiswerk-en-vragentopic

quote:

Op zondag 21 november 2010 15:51 schreef keesjeislief het volgende:

[..]



Dat dy/dx =-x/y volgt uit 2 x + 2 y (dy/dx) =0, dat geldt inderdaad (natuurlijk) alleen in dit specifieke geval. Als je bijv. zou hebben 4 x + 6 y^3 = 5 krijg je dy/dx = -4/(18 y^2), kun je dat zelf narekenen?

Ja dat moest ik even weten, ik heb hier ter illustratie wat echter krijg als ik dat dus toepas bij de opgave over Van der Waals vergelijking. (Aangenomen dat V en P de enige variabelen zijn)
Ik heb niet echt het idee dat dit de bedoeling is...

quote:

Op zondag 21 november 2010 15:59 schreef Fingon het volgende:

[..]


Ja dat moest ik even weten, ik heb hier ter illustratie wat echter krijg als ik dat dus toepas bij de opgave over Van der Waals vergelijking. (Aangenomen dat V en P de enige variabelen zijn)
Ik heb niet echt het idee dat dit de bedoeling is...
[ afbeelding ]

_{Als je continu de goedbedoelde adviezen en vragen overslaat kan het gebeuren dat mensen je vanaf een bepaald moment niet meer willen helpen} . De tweede regel klopt al niet, om dV/dP te bepalen ga je de hele vergelijking differentieren naar P, oftewel aan beide kanten de operator d/dP toepassen. Waar jij er links en rechts een dV/dP voor gezet hebt moet het dus een d/dP zijn. (En V' is moet je niet gebruiken in deze context). Je idee om de produktregel te gebruiken is wel prima. . Je kunt het bijv. als volgt doen:

Ik heb dus gewoon foute notatie gebruikt want wat je zegt was dus wel mijn bedoeling, V' staat voor dV/dP.
Verder mijn excuses als jij meent dat ik je goede advies negeer, dat doe ik beslist niet bewust...
Daarom dit even uitgewerkt:
4 x + 6 y^3 = 5
d/dx(4x + 6y^3) = d/dx(5)
4 + 12y^2*dy/dx = 0
12y^2 * dy/dx = -4
dy/dx = -4/12y^2

Tenslotte zijn zowel mijn als volgens mij jouw afgeleide eveneens fout volgens mijn antwoordmodel, Ik keek net en het gaf als antwoord mijn afgeleide maar zonder de term 2abn^2*V^-2 in de noemer.

Hmm, ik zit weer met een nieuwe

[quote]Bereken algebraïsch voor welke waarden van q de lijn m: y = -8x+q de grafiek van h(x)=2x/(√(x²+4))[/quote]
Dus ik h'(x) berekenen om daarna h'(x)*-8=-1 te doen, krijg ik 2*(x²+4)-2x²/(x²+4)√(x²+4) , wat volgens de uitwerking ook klopt.
Dan staat er echter 2*(x²+4)-2x²/(x²+4)√(x²+4)=8/(x²+4)√(x²+4)
Ik zie niet hoe ze erbij komen dat 2*(x²+4)-2x² = 8

Wat zie ik hier niet?

Hmm, ik ben wel heel blind, ik zie het nu
Toch maar eens aan de bril..

[ Bericht 10% gewijzigd door Thas op 21-11-2010 17:47:44 ]

quote:

Op zondag 21 november 2010 15:07 schreef BasementDweller het volgende:

[..]


Waar heb je een overzichtje met al die codes, of weet je ze uit je hoofd?

Vroeger kon je hier gewoon alles typen wat je wilde, in Unicode. Met de 'nieuwe' layout gaat dat niet meer en moet je HTML escape codes gebruiken. Met 'dank' aan Danny die anno 2010 denkt dat support voor Unicode niet nodig is op een NL forum.

quote:

Op zondag 21 november 2010 17:21 schreef Fingon het volgende:
Ik heb dus gewoon foute notatie gebruikt want wat je zegt was dus wel mijn bedoeling, V' staat voor dV/dP.
Verder mijn excuses als jij meent dat ik je goede advies negeer, dat doe ik beslist niet bewust...
Daarom dit even uitgewerkt:
4 x + 6 y^3 = 5
d/dx(4x + 6y^3) = d/dx(5)
4 + 12y^2*dy/dx = 0
12y^2 * dy/dx = -4
dy/dx = -4/12y^2

Tenslotte zijn zowel mijn als volgens mij jouw afgeleide eveneens fout volgens mijn antwoordmodel, Ik keek net en het gaf als antwoord mijn afgeleide maar zonder de term 2abn^2*V^-2 in de noemer.

Ok. . Het leek er even op dat je alleen geinteresseerd was in een kant-en-klare uitwerking, excusez-moi. Alleen is 3*6=18, geen 12. . Ik zie niet zo snel waar ik een fout gemaakt zou hebben, zou je misschien nog eens de exacte opgave en het verwachte antwoord kunnen posten, zodat we kunnen uitsluiten dat er ergens een typo oid zit?

quote:

Op zondag 21 november 2010 17:24 schreef Riparius het volgende:

[..]



Vroeger kon je hier gewoon alles typen wat je wilde, in Unicode. Met de 'nieuwe' layout gaat dat niet meer en moet je HTML escape codes gebruiken. Met 'dank' aan Danny die anno 2010 denkt dat support voor Unicode niet nodig is op een NL forum.

Hoe typ je eigenlijk unicodekarakters die niet op je toetsenbord zitten? . Is dat makkelijker dan het typen van HTML-codes? Zou het niet mogelijk zijn om een Latex-parsertje op de server neer te zetten, zodat we $<latex-code>$ in de tekst kunnen gebruiken?

quote:

Op zondag 21 november 2010 18:13 schreef keesjeislief het volgende:

[..]



Hoe typ je eigenlijk unicodekarakters die niet op je toetsenbord zitten? . Is dat makkelijker dan het typen van HTML-codes? Zou het niet mogelijk zijn om een Latex-parsertje op de server neer te zetten, zodat we $<latex-code>$ in de tekst kunnen gebruiken?

Ik gebruik een speciale keyboard utility (Tavultesoft Keyman) waarmee ik heel eenvoudig kan switchen naar bijvoorbeeld (klassiek) Grieks of Cyrillisch schrift en allerlei diacritica kan typen middels user-defined keyboard layouts. Support voor Latex is ook een idee, maar alle moderne OSsen en applicaties die met tekst werken ondersteunen Unicode, dus dat zou prioriteit moeten hebben. De klok is hier met de opgelegde New Decade layout 10 jaar teruggezet, en dat is een slechte zaak, ook voor dit wiskunde topic.

[ Bericht 21% gewijzigd door Riparius op 21-11-2010 18:51:18 ]

hebben ze unicode uitgeschakeld ?

test: V W

edit: Ja, maar niet in het edit window zelf

quote:

Op zondag 21 november 2010 18:35 schreef GlowMouse het volgende:
Als je auto-updates in een topic uitzet, kun je weer unicode posten. Een andere fix moet ik nog eens naar kijken.

Het viel me net pas op dat jouw http://betahw.mine.nu/index.php werkt door de ge-escapede Latex-code mee te geven aan het cgi-script dat vervolgens een plaatje teruggeeft. Dan zou het in principe mogelijk moeten zijn om een custom tagje toe te voegen zodat je [tagje]<latex-code>[/tagje] kunt typen en dat dat door de parser wordt omgezet naar , of niet? Zou dat een mogelijkheid zijn, of zitten daar toch teveel haken en ogen aan?

ach, we hebben hier sup en sub tags en daar kan je al een heel eind mee komen.

quote:

Op zondag 21 november 2010 19:03 schreef keesjeislief het volgende:

[..]



Het viel me net pas op dat jouw http://betahw.mine.nu/index.php werkt door de ge-escapede Latex-code mee te geven aan het cgi-script dat vervolgens een plaatje teruggeeft. Dan zou het in principe mogelijk moeten zijn om een custom tagje toe te voegen zodat je [tagje]<latex-code>[/tagje] kunt typen en dat dat door de parser wordt omgezet naar
[ code verwijderd ]

, of niet? Zou dat een mogelijkheid zijn, of zitten daar toch teveel haken en ogen aan?

Dat zou ideaal zijn en klinkt simpel

quote:

Op zondag 21 november 2010 18:08 schreef keesjeislief het volgende:

[..]



Ok. . Het leek er even op dat je alleen geinteresseerd was in een kant-en-klare uitwerking, excusez-moi. Alleen is 3*6=18, geen 12. . Ik zie niet zo snel waar ik een fout gemaakt zou hebben, zou je misschien nog eens de exacte opgave en het verwachte antwoord kunnen posten, zodat we kunnen uitsluiten dat er ergens een typo oid zit?

De opgave was dus: geef dV/dP van deze functie

Het is een boek dat zoveel mogelijk real-world voorbeelden geeft vandaar deze Van der Waalsvergelijking over volume en dichtheid etc van een gas.
ik mocht aannemen dat alles behalve V en P dus constant waren, R is bijvoorbeeld die universele gasconstante etc.
In ieger geval is dat alles wat erbij staat, daarna staat bij de antwoorden:

Ze hebben dus maal V^3 gedaan dus dat maakt geen verschil met mijn oplossing, en zoals je ziet is er maar 1 term verschil met mijn oplossing, die dus blijkbaar ergens 0 was geworden.
Waarschijnlijk in het geweld van die kettingregel met alle breuken ergens een foutje aan mijn kant, maar goed.

quote:

Op zondag 21 november 2010 19:38 schreef Fingon het volgende:

[..]


De opgave was dus: geef dV/dP van deze functie
[ afbeelding ]
Het is een boek dat zoveel mogelijk real-world voorbeelden geeft vandaar deze Van der Waalsvergelijking over volume en dichtheid etc van een gas.
ik mocht aannemen dat alles behalve V en P dus constant waren, R is bijvoorbeeld die universele gasconstante etc.
In ieger geval is dat alles wat erbij staat, daarna staat bij de antwoorden:
[ afbeelding ]
Ze hebben dus maal V^3 gedaan dus dat maakt geen verschil met mijn oplossing, en zoals je ziet is er maar 1 term verschil met mijn oplossing, die dus blijkbaar ergens 0 was geworden.
Waarschijnlijk in het geweld van die kettingregel met alle breuken ergens een foutje aan mijn kant, maar goed.

Oh, nondeju, ik heb inderdaad wel een fout gemaakt op mijn laatste regel, sorry . Maar goed, dan zijn we eruit?

quote:

Op zondag 21 november 2010 20:28 schreef keesjeislief het volgende:

[..]



Oh, nondeju, ik heb inderdaad wel een fout gemaakt op mijn laatste regel, sorry . Maar goed, dan zijn we eruit?

Ja, behalve dat ik bij mezelf nog ff de fout moet gaan zoeken Maar niet getreurd, ik heb een nieuwe opgave als je zin hebt
Dit is de situatie, je hebt zo'n mooie lamp die een schaduw werpt om een object, en de locatie van de omtrek van dat object is dus die ellips gegeven door x^2+4y^2=5
nu moet ik dus berekenen hoe hoog die lamp staat.
Ik zat te denken om te kijken of ik bv die hoek bij het punt (-5,0) zou kunnen vinden maar hoe heb ik geen idee, op 1 of andere manier moet ik het snijpunt van de ellips met 1 van die lijnen vinden maar ik zie niet hoe dat te doen met de beschikbare informatie.

Heb je een hint?
Als ik hier de impliciete afgeleide zou ik natuurlijk de coefficient van de raaklijn krijgen maar daarvoor moet ik eerst weten in welk punt het zit..

quote:

Op zondag 21 november 2010 20:48 schreef Fingon het volgende:

[..]


Ja, behalve dat ik bij mezelf nog ff de fout moet gaan zoeken Maar niet getreurd, ik heb een nieuwe opgave als je zin hebt
Dit is de situatie, je hebt zo'n mooie lamp die een schaduw werpt om een object, en de locatie van de omtrek van dat object is dus die ellips gegeven door x^2+4y^2=5
nu moet ik dus berekenen hoe hoog die lamp staat.
Ik zat te denken om te kijken of ik bv die hoek bij het punt (-5,0) zou kunnen vinden maar hoe heb ik geen idee, op 1 of andere manier moet ik het snijpunt van de ellips met 1 van die lijnen vinden maar ik zie niet hoe dat te doen met de beschikbare informatie.
[ afbeelding ]
Heb je een hint?
Als ik hier de impliciete afgeleide zou ik natuurlijk de coefficient van de raaklijn krijgen maar daarvoor moet ik eerst weten in welk punt het zit..

Hier is de extragratis hint: die bovenste grijze lijn is een raaklijn aan de kromme in een onbekend punt (x_0,y_0), en hij gaat ook nog door het punt (-5,0). Als je nu voor een willekeurig punt (x_0,y_0) de bijbehorende raaklijn bepaalt, en vervolgens uitvist hoe je die (x_0,y_0) moet kiezen om ook nog te hebben dat betreffende raaklijn door (-5,0) gaat? Of, misschien slimmer, als je alle lijnen door (-5,0) bekijkt, d.w.z. y=a*x+5 a, dan is de gezochte lijn de enige die precies een snijpunt met de kromme heeft, alle anderen hebben ofwel twee snijpunten ofwel helemaal geen. Misschien is dat voldoende om de a te bepalen?

quote:

Op zondag 21 november 2010 20:48 schreef Fingon het volgende:

[..]

Dit is de situatie, je hebt zo'n mooie lamp die een schaduw werpt om een object, en de locatie van de omtrek van dat object is dus die ellips gegeven door x^2+4y^2=5
Nu moet ik dus berekenen hoe hoog die lamp staat.
Ik zat te denken om te kijken of ik b.v. die hoek bij het punt (-5,0) zou kunnen vinden maar hoe heb ik geen idee, op 1 of andere manier moet ik het snijpunt van de ellips met 1 van die lijnen vinden maar ik zie niet hoe dat te doen met de beschikbare informatie.
[ afbeelding ]
Heb je een hint?
Als ik hier de impliciete afgeleide neem zou ik natuurlijk de coëfficiënt van de raaklijn krijgen maar daarvoor moet ik eerst weten in welk punt het zit..

Je hebt alleen de bovenste helft van de ellips nodig. Deze kun je beschouwen als de grafiek van de functie:

(1) f(x) = (1/2)*(5 - x²)^1/2

De afgeleide van deze functie is:

(2) f'(x) = -(1/2)*x*(5 - x²)^-1/2

Essentiëel is nu dat je ziet dat de richtingscoëfficiënt van de raaklijn gelijk is aan de afgeleide in het raakpunt. Laten we zeggen dat de x-coördinaat van het raakpunt p is, dan is de y-coördinaat f(p) en geldt voor de richtingscoëfficiënt m van de raaklijn dus:

(3) m = f'(p)

Nu gaat de raaklijn zowel door het punt (-5;0) als door het raakpunt (p;f(p)), dus kunnen we ook zeggen dat voor de richtingscoëfficiënt m geldt:

(4) m = f(p)/(p+5)

Uit (3) en (4) volgt dus:

(5) f'(p) = f(p)/(p+5)

Dit is een vergelijking in p, die je op kunt lossen als je met behulp van (1) en (2) de uitdrukkingen voor f(p) en f'(p) in (5) invult.

Als je het goed doet vind je als oplossing voor (5) p = -1. De richtingscoëfficiënt m = f'(p) van de raaklijn is dus f'(-1) = 1/4, en daaruit volgt direct dat de lichtbron zich in het punt (3;2) bevindt. De gezochte hoogte bedraagt dus 2.

[ Bericht 3% gewijzigd door Riparius op 22-11-2010 00:06:23 ]

Toevallig iemand nog wakker die duidelijk het verschil tussen een rekenkundige / meetkundige - rij / reeks kan uitleggen? Liefst met een voorbeeld als dat kan, zonder is ook goed natuurlijk!

quote:

Op maandag 22 november 2010 01:20 schreef Turalyon het volgende:
Toevallig iemand nog wakker die duidelijk het verschil tussen een rekenkundige / meetkundige - rij / reeks kan uitleggen? Liefst met een voorbeeld als dat kan, zonder is ook goed natuurlijk!

Staat gewoon op wikipedia, of begrijp je dat niet?

quote:

Op maandag 22 november 2010 01:25 schreef minibeer het volgende:

[..]

Staat gewoon op wikipedia, of begrijp je dat niet?

Dankje. Een reeks is oneindig en een rij eindig toch?

quote:

Op maandag 22 november 2010 01:54 schreef Turalyon het volgende:

[..]



Dankje. Een reeks is oneindig en een rij eindig toch?

Nee.

Reeks is een ander woord voor een rij van partiële sommen. Een reeks en een rij kunnen elk zowel een eindig als een oneindig aantal elementen hebben. Maar het is inderdaad wel zo dat met 'reeksen' doorgaans oneindige reeksen worden bedoeld. Lees dit eens.

[ Bericht 14% gewijzigd door Riparius op 22-11-2010 11:36:59 ]

Voor degenen die het (ook) makkelijk vinden: op http://www.maths.bath.ac.uk/~kvs20/tools/fok/tex_parser.html staat een dun schilletje om de parser van Glowmouse's http://betahw.mine.nu/index.php. Het idee is dat je eerst 'gewoon' je post kunt tikken met Latex-code erin, bijv.


, dan kopieer en plak je de inhoud van je post in het bovenste tekstvak van genoemde website, drukt op 'parse', kopieert vervolgens de output en plakt die hier op fok weer in het invoerscherm. Bovenstaande zou bijv. worden:


Het is natuurlijk nog steeds een heen-en-weer gekopie-en-plak, maar ik vind het persoonlijk in ieder geval wel handiger om niet voor elke uitdrukking steeds naar de site van Glowmouse te hoeven. Glowmouse, als je om wat voor reden dan ook een probleem met het op deze manier gebruiken van jouw website hebt hoor ik het van je.