SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
bij 1 zou ik 1/n<a iets uitgebreider motiveren: 1<a dus n < na dus 1 < na en vermenigvuldigen met het positief getal 1/n (waarom positief?) levert 1/n < a.
de laatste dus bij 2 gaat ook wel heel snel.
de laatste dus bij 2 gaat ook wel heel snel.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
ik wil het aantonen voor n>1, voor n=2 klopt het, maar nu voor n>2quote:Op dinsdag 16 februari 2010 13:55 schreef GlowMouse het volgende:
Waarom zou je n=3 nodig hebben om het gevraagde aan te tonen?
daarom keek ik naar 3 en zag dat ik terug uit kom op n=2
Je wilt aantonen dat de groep Abels is. Je hebt aangetoond ab=ba. Wat wil je nog meer aantonen?quote:Op dinsdag 16 februari 2010 14:18 schreef JoPiDo het volgende:
[..]
ik wil het aantonen voor n>1, voor n=2 klopt het, maar nu voor n>2
daarom keek ik naar 3 en zag dat ik terug uit kom op n=2
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
ik heb aangetoond dat het voor n=2 geldt, maar niet voor n>2, dat moet ik ook aantonenquote:Op dinsdag 16 februari 2010 14:20 schreef GlowMouse het volgende:
[..]
Je wilt aantonen dat de groep Abels is. Je hebt aangetoond ab=ba. Wat wil je nog meer aantonen?
Wat heeft commutativiteit met n te maken?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
??quote:Op dinsdag 16 februari 2010 14:29 schreef GlowMouse het volgende:
Wat heeft commutativiteit met n te maken?
hoe laat ik zien dat het geldt voor n>2? dat is niet zo'n heel rare vraag...?
Dat hoef je niet te bewijzen, er is alleen gegeven dat het voor alle n geldt. Er staat niet dat je voor alle n moet bewijzen dat G abels is.quote:Op dinsdag 16 februari 2010 14:34 schreef JoPiDo het volgende:
[..]
??
hoe laat ik zien dat het geldt voor n>2? dat is niet zo'n heel rare vraag...?
WEB / [HaxBall #64] Jos is God
Arguing on the Internet is like running in the Special Olympics.
Arguing on the Internet is like running in the Special Olympics.
V is het vlakdeel dat wordt ingesloten door de grafiek van f(x) = 8/x^2, de x-as, de yas en de lijnen x=8 en y=8.
Bereken de oppervlakte van V.
Om de een of andere reden zie ik niet wat ik fout doe/anders moet doen?
Ik bereken totale oppervlakte onder lijn x en y ( dus 7 x 8 = 56)
Primitiveer f(x), F(x) = -8x^-1.
Dan is het dus 56 - [F(x)]1tm8 = 56 - 7 = 49
|Maar dat klopt niet..
Bereken de oppervlakte van V.
Om de een of andere reden zie ik niet wat ik fout doe/anders moet doen?
Ik bereken totale oppervlakte onder lijn x en y ( dus 7 x 8 = 56)
Primitiveer f(x), F(x) = -8x^-1.
Dan is het dus 56 - [F(x)]1tm8 = 56 - 7 = 49
|Maar dat klopt niet..
Als je een figuur tekent, zie je dat je nu de oppervlakte bepaalt van het stuk begrensd door de grafiek, de lijn y=8 en de lijn x=8.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Heb ik gedaan, daarom heb ik ook de oppervlakte van x = 1 tm 8 onder de y=8 lijn uitgerekend (wat 8x7 is.) en dan min de oppervlakte onder de f(x) lijn (van x=1 tm 8)quote:Op dinsdag 16 februari 2010 15:23 schreef GlowMouse het volgende:
Als je een figuur tekent, zie je dat je nu de oppervlakte bepaalt van het stuk begrensd door de grafiek, de lijn y=8 en de lijn x=8.
Ah ik zie het al, ik heb de vraag verkeerd begrepen!
Bedankt, nu klopt het!
Ik zit nog eens te kijken, maar kan ik egienlijk niet net als ik bij 2 doe bij 1 gelijk zeggen dat voor elke n>1 1/n<a, omdat a >=1 ?quote:Op dinsdag 16 februari 2010 14:11 schreef GlowMouse het volgende:
bij 1 zou ik 1/n<a iets uitgebreider motiveren: 1<a dus n < na dus 1 < na en vermenigvuldigen met het positief getal 1/n (waarom positief?) levert 1/n < a.
de laatste dus bij 2 gaat ook wel heel snel.
de stap van n>1 naar 1/n < 1 moet uiteraard gemotiveerd worden; het is allemaal evenveel werk.quote:
[..]
Ik zit nog eens te kijken, maar kan ik egienlijk niet net als ik bij 2 doe bij 1 gelijk zeggen dat voor elke n>1 1/n<a, omdat a >=1 ?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ah, oké.
Een andere vraag dan: Ik moet bewijzen dat een ondergroep in een abelse groep ook abels is. Maar een ondergroep heeft toch altijd dezelfde bewerking als de normale groep, en is dus automatisch abels? Valt daar nog iets in te bewijzen?
Daarna "geef een niet-triviaal voorbeeld van een abelse ondergroep van een niet-abelse groep", een groep met drie elementen {e, a, a-1} met orde van a is 2 is zeker triviaal?
Een andere vraag dan: Ik moet bewijzen dat een ondergroep in een abelse groep ook abels is. Maar een ondergroep heeft toch altijd dezelfde bewerking als de normale groep, en is dus automatisch abels? Valt daar nog iets in te bewijzen?
Daarna "geef een niet-triviaal voorbeeld van een abelse ondergroep van een niet-abelse groep", een groep met drie elementen {e, a, a-1} met orde van a is 2 is zeker triviaal?
Die eerste lijkt me triviaal om te bewijzen ja.
{e} lijkt me zeker triviaal, die van jou weet ik niet.
{e} lijkt me zeker triviaal, die van jou weet ik niet.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
*ziet wiskunde in de topictitel staan*
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik ben bezig met verzamelingsleer. Waar ik niet helemaal aan uit kom met de informatie die ik heb.
Ik heb verzameling A = {a,b,c} . Eenvoudig. Van A* zijn bv woorden als aa,bb en cc te maken
Wat als een element een verzameling opzich is? Dus B = {a,b,{c,d}} . Wat zijn van B* woorden die ik kan maken op aa en bb na?
Ik heb verzameling A = {a,b,c} . Eenvoudig. Van A* zijn bv woorden als aa,bb en cc te maken
Wat als een element een verzameling opzich is? Dus B = {a,b,{c,d}} . Wat zijn van B* woorden die ik kan maken op aa en bb na?
Wel, bijvoorbeeld iets als ab{c,d}bba.quote:Op dinsdag 16 februari 2010 21:12 schreef Keiichi het volgende:
Ik ben bezig met verzamelingsleer. Waar ik niet helemaal aan uit kom met de informatie die ik heb.
Ik heb verzameling A = {a,b,c} . Eenvoudig. Van A* zijn bv woorden als aa,bb en cc te maken
Wat als een element een verzameling opzich is? Dus B = {a,b,{c,d}} . Wat zijn van B* woorden die ik kan maken op aa en bb na?
als
2log(1+t0) = log(1+t0+T)
en T is hier de verdubbelingstijd, wat is dan T?
het antwoord is T = t0 + t2boven0
in eerste instantie herken ik die notatie niet, t en dan twee cijfers boven elkaar, weet iemand wat dit betekent?
en ten tweede begrijp ik sowieso niet hoe je dit moet oplossen..
2log(1+t0) = log(1+t0+T)
en T is hier de verdubbelingstijd, wat is dan T?
het antwoord is T = t0 + t2boven0
in eerste instantie herken ik die notatie niet, t en dan twee cijfers boven elkaar, weet iemand wat dit betekent?
en ten tweede begrijp ik sowieso niet hoe je dit moet oplossen..
Nee, met triviaal wordt {e} bedoeld.quote:Op dinsdag 16 februari 2010 16:39 schreef Hanneke12345 het volgende:
Ah, oké.
Een andere vraag dan: Ik moet bewijzen dat een ondergroep in een abelse groep ook abels is. Maar een ondergroep heeft toch altijd dezelfde bewerking als de normale groep, en is dus automatisch abels? Valt daar nog iets in te bewijzen?
Daarna "geef een niet-triviaal voorbeeld van een abelse ondergroep van een niet-abelse groep", een groep met drie elementen {e, a, a-1} met orde van a is 2 is zeker triviaal?
Dat lijkt me gewoon machtsverheffen:quote:
als
2log(1+t0) = log(1+t0+T)
en T is hier de verdubbelingstijd, wat is dan T?
het antwoord is T = t0 + t2boven0
in eerste instantie herken ik die notatie niet, t en dan twee cijfers boven elkaar, weet iemand wat dit betekent?
en ten tweede begrijp ik sowieso niet hoe je dit moet oplossen..
heb je een plaatje van de opgave, want ik snap je notatie niet.
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:38:24 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Je kunt een superscript met [sup] en [ /sup] en een subscript tussen [sub] en [ /sub] (maar dan zonder spaties). Misschien maakt dat je opgave wat leesbaarder.quote:Op dinsdag 16 februari 2010 21:37 schreef poesemuis het volgende:
als
2log(1+t0) = log(1+t0+T)
en T is hier de verdubbelingstijd, wat is dan T?
het antwoord is T = t0 + t2boven0
in eerste instantie herken ik die notatie niet, t en dan twee cijfers boven elkaar, weet iemand wat dit betekent?
en ten tweede begrijp ik sowieso niet hoe je dit moet oplossen..
het is een t, en direct daarna twee cijfers, eentje boven en eentje onder, de 2 boven en de 0 daaronder, geen machtnotatiequote:Op dinsdag 16 februari 2010 21:47 schreef thabit het volgende:
[..]
Je kunt een superscript met [sup] en [ /sup] en een subscript tussen [sub] en [ /sub] (maar dan zonder spaties). Misschien maakt dat je opgave wat leesbaarder.
Probeer dan die log eens weg te werken door links en rechts een e-macht te nemen (of wat voor grondtal je standaard voor logaritmen hanteert).
oh god ik denk dat mijn antwoordenboekje hier toch een machtnotatie bedoelde 
wat stom
want zo klopt het toch:
2log(1+t0) = log(1+t0+T)
log((1+t0)^2) = log(1+t0+T)
(1+t0)^2 = 1+t0+T
1 + 2t0 + t0^2 = 1+t0+T
T = t0 + t0^2
wat stomwant zo klopt het toch:
2log(1+t0) = log(1+t0+T)
log((1+t0)^2) = log(1+t0+T)
(1+t0)^2 = 1+t0+T
1 + 2t0 + t0^2 = 1+t0+T
T = t0 + t0^2
Om te beginnen: gebruik alsjeblieft een duidelijke notatie, subscript en superscript zijn er niet voor niks. Nu is het zo dat iemand eerst je opgave moet ontcijferen om überhaupt te kunnen snappen wat de vraag is. En dat geldt helaas niet alleen voor jou.quote:Op dinsdag 16 februari 2010 21:37 schreef poesemuis het volgende:
als
2log(1+t0) = log(1+t0+T)
en T is hier de verdubbelingstijd, wat is dan T?
het antwoord is T = t0 + t2boven0
in eerste instantie herken ik die notatie niet, t en dan twee cijfers boven elkaar, weet iemand wat dit betekent?
en ten tweede begrijp ik sowieso niet hoe je dit moet oplossen..
Wat ik eruit opmaak is dat je hebt:
2∙log(1 + t0) = log(1 + t0 + T)
Dan hebben we dus:
(1 + t0)2 = 1 + t0 + T
En dus:
T = (1 + t0)2 - t0 - 1
En uitwerken geeft dan:
T = t0 + t02
De nul in t0 is een index en de twee in t02 een kwadraat, niks bijzonders dus.
Ik weet niet wat dat sub en sub is.. maar ik zal eens uitzoekenquote:Op dinsdag 16 februari 2010 22:34 schreef Riparius het volgende:
[..]
Om te beginnen: gebruik alsjeblieft een duidelijke notatie, subscript en superscript zijn er niet voor niks. Nu is het zo dat iemand eerst je opgave moet ontcijferen om überhaupt te kunnen snappen wat de vraag is. En dat geldt helaas niet alleen voor jou.
Wat ik eruit opmaak is dat je hebt:
2∙log(1 + t0) = log(1 + t0 + T)
Dan hebben we dus:
(1 + t0)2 = 1 + t0 + T
En dus:
T = (1 + t0)2 - t0 - 1
En uitwerken geeft dan:
T = t0 + t02
De nul in t0 is een index en de twee in t02 een kwadraat, niks bijzonders dus.
Vraagje:
De verdubbelingstijd van 1+bt ,met t=tijd en b=positieve constante, verdubbelingstijd in T
het antwoord moet zijn T = (1/b) + t0 (t-nul staat daar)
ik begrijp niet hoe je daaraan komt, iemand?
hoe ik begonnen was:
2(1+bt0) = 1 + bt0 + T
2 + 2bt0 = 1 + bt0 + T
T = 1 + bt0
De verdubbelingstijd van 1+bt ,met t=tijd en b=positieve constante, verdubbelingstijd in T
het antwoord moet zijn T = (1/b) + t0 (t-nul staat daar)
ik begrijp niet hoe je daaraan komt, iemand?
hoe ik begonnen was:
2(1+bt0) = 1 + bt0 + T
2 + 2bt0 = 1 + bt0 + T
T = 1 + bt0
Als je een getal onderaan wilt zetten moet je het tussen [sub ] en [/sub ] zetten (zonder de spaties) en bovenin tussen [sup ] en [/sup]. Dat maakt je opgaven een stuk leesbaarder en kunnen mensen hier je dus beter en sneller helpen. Je kunt ook het cijfer selecteren en dan op die knopjes met x2 en x2 drukken.
"Reality is an illusion created by a lack of alcohol."
quote:Op dinsdag 16 februari 2010 14:44 schreef -jos- het volgende:
[..]
Dat hoef je niet te bewijzen, er is alleen gegeven dat het voor alle n geldt. Er staat niet dat je voor alle n moet bewijzen dat G abels is.
sorry, jullie hebben helemaal gelijk!
ik was in de war, er wordt natuurlijk maar 1 groep bedoeld waarop deze bewerking geldt en ik had in mijn hoofd verschillende groepen waarin voor elke groep de n anders is
Als
xn+1 = a(1-xn) = xn (omdat we te maken hebben met een evenwichtspunt)
waarom is dan xn = a / (1+a)?
xn+1 = a(1-xn) = xn (omdat we te maken hebben met een evenwichtspunt)
waarom is dan xn = a / (1+a)?
Kun je lineaire vergelijkingen oplossen? Het is de oplossing van x = a(1-x).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Elementaire algebra. Als:quote:Op woensdag 17 februari 2010 16:23 schreef poesemuis het volgende:
Als
xn+1 = a(1-xn) = xn (omdat we te maken hebben met een evenwichtspunt)
waarom is dan xn = a / (1+a)?
xn = a∙(1 - xn),
Dan is:
xn = a - a∙xn,
En dus:
xn + a∙xn = a,
Dus:
xn∙(1 + a) = a,
Dus:
xn = a/(1 + a)
Welke vooropleiding heb je eigenlijk? Dit zou toch geen probleem mogen zijn ...
Ik heb een vraag over de cosinus regel. Ik neem aan dat hij bekend is. Maar ik zal hem voor de duidelijkheid herhalen:
Voor de drie zijden a, b en c van een driehoek als ook voor de tegenover de zijde c liggende hoek, dat wil zeggen de door de twee zijden, a en b ingesloten hoek, γ geldt:
c^2 = a^2 + b^2 - 2 a b cos©
Als je het bewijs van de cosinus regel bekijkt dan zie je in dat dit een implicatie is in de vorm A impliceert B. Dus een Als..., dan.... stelling. A is de hypothese en B is dan de conclusie. In dit geval is de conclusie duidelijk c^2 = a^2 + b^2 - 2 a b cos©.
Nu lees ik in een boek dat de converse van de cosinus regel niet waar is. Met converse bedoel ik het verwisselen van de hypothese met de conclusie. Dus B impliceert A. Volgens het boek komt dit omdat in het bewijs van de cosinus regel gebruik wordt gemaakt van de stelling van Pythagoras. Dit klopt maar wat is de samenhang met de converse? Dit ontgaat mij. kan iemand me uitleggen waarom de converse niet waar is? Hetzij met een tegenvoorbeeld of logisch argument.
Voor de drie zijden a, b en c van een driehoek als ook voor de tegenover de zijde c liggende hoek, dat wil zeggen de door de twee zijden, a en b ingesloten hoek, γ geldt:
c^2 = a^2 + b^2 - 2 a b cos©
Als je het bewijs van de cosinus regel bekijkt dan zie je in dat dit een implicatie is in de vorm A impliceert B. Dus een Als..., dan.... stelling. A is de hypothese en B is dan de conclusie. In dit geval is de conclusie duidelijk c^2 = a^2 + b^2 - 2 a b cos©.
Nu lees ik in een boek dat de converse van de cosinus regel niet waar is. Met converse bedoel ik het verwisselen van de hypothese met de conclusie. Dus B impliceert A. Volgens het boek komt dit omdat in het bewijs van de cosinus regel gebruik wordt gemaakt van de stelling van Pythagoras. Dit klopt maar wat is de samenhang met de converse? Dit ontgaat mij. kan iemand me uitleggen waarom de converse niet waar is? Hetzij met een tegenvoorbeeld of logisch argument.
-
De cosinusfunctie is injectief op [0, pi] dus het enige dat fout zou kunnen gaan is de driehoeksongelijkheid: misschien is het mogelijk om een viertal (a,b,c,gamma) te vinden dat aan de cosinusregel voldoet maar bijvoorbeeld niet a <= b + c. Als inderdaad a > b + c geldt dan hebben we c < a - b en dus c2 < a2 + b2 - 2ab. Ofwel 2ab*cos(gamma) > 2ab. Maar de cosinus zit altijd op het interval [-1,1] dus die driehoeksongelijkheid moet gewoon gelden. Evenzo voor de andere driehoeksongelijkheden.quote:Op woensdag 17 februari 2010 22:03 schreef gaussie het volgende:
Ik heb een vraag over de cosinus regel. Ik neem aan dat hij bekend is. Maar ik zal hem voor de duidelijkheid herhalen:
Voor de drie zijden a, b en c van een driehoek als ook voor de tegenover de zijde c liggende hoek, dat wil zeggen de door de twee zijden, a en b ingesloten hoek, γ geldt:
c^2 = a^2 + b^2 - 2 a b cos©
Als je het bewijs van de cosinus regel bekijkt dan zie je in dat dit een implicatie is in de vorm A impliceert B. Dus een Als..., dan.... stelling. A is de hypothese en B is dan de conclusie. In dit geval is de conclusie duidelijk c^2 = a^2 + b^2 - 2 a b cos©.
Nu lees ik in een boek dat de converse van de cosinus regel niet waar is. Met converse bedoel ik het verwisselen van de hypothese met de conclusie. Dus B impliceert A. Volgens het boek komt dit omdat in het bewijs van de cosinus regel gebruik wordt gemaakt van de stelling van Pythagoras. Dit klopt maar wat is de samenhang met de converse? Dit ontgaat mij. kan iemand me uitleggen waarom de converse niet waar is? Hetzij met een tegenvoorbeeld of logisch argument.
De 'converse' geldt dus gewoon.
Het is nu veel duidelijker. Dit is gewoon een fout in het boek. Heb je misschien een bewijs van de converse? Ik kan hem namelijk nergens vinden....
-
Kun je even vertellen in welk boek dat staat? Of letterlijk citeren wat het boek hierover zegt?quote:Op woensdag 17 februari 2010 22:03 schreef gaussie het volgende:
Nu lees ik in een boek dat de converse van de cosinus regel niet waar is. Met converse bedoel ik het verwisselen van de hypothese met de conclusie. Dus B impliceert A. Volgens het boek komt dit omdat in het bewijs van de cosinus regel gebruik wordt gemaakt van de stelling van Pythagoras. Dit klopt maar wat is de samenhang met de converse? Dit ontgaat mij. kan iemand me uitleggen waarom de converse niet waar is? Hetzij met een tegenvoorbeeld of logisch argument.
Mijn post was een bewijs, ik zal het argument even verduidelijken:quote:Op woensdag 17 februari 2010 22:35 schreef gaussie het volgende:
Het is nu veel duidelijker. Dit is gewoon een fout in het boek. Heb je misschien een bewijs van de converse? Ik kan hem namelijk nergens vinden....
Neem een viertal (a, b, c, gamma), met a,b,c > 0 en gamma in [0, pi] dat aan de vergelijking in de cosinusregel voldoet. Dan geldt voor a, b, c de driehoeksongelijkheid (omdat cos(gamma) in [-1, 1] zit, probeer maar uit te werken). Er is dus een driehoek met zijden a, b, c. De driehoek zal ook een hoek tegenover c hebben, noem deze hoek gamma'. Voor gamma' geldt dat het in [0, pi] zit en aan de cosinusregel voldoet. Omdat gamma daar ook aan voldoet, geldt cos(gamma) = cos(gamma'). Maar dan ook gamma = gamma' want op [0,pi] is de cosinusfunctie strikt dalend van 1 naar -1 en kan dus twee verschillende gammas dezelfde waarde aannemen.
weet iemand een groep met oneindige orde, waarin elk element eindige orde heeft?
ik kan echt niets bedenken!
ik kan echt niets bedenken!
Q/Zquote:Op donderdag 18 februari 2010 23:36 schreef JoPiDo het volgende:
weet iemand een groep met oneindige orde, waarin elk element eindige orde heeft?
ik kan echt niets bedenken!
Ik weet niet of dit de geschikte is (of dat ik de beta overig moet gebruiken), maar het leek me het meest logisch mijn vraag hier te plaatsen aangezien het om een wiskundige relatie gaat tussen twee waarden en mijn wiskundeknobbel het even laat afweten hoe ik dit op een logische manier beschrijf dat er een relatie onderling bevindt.
Intro:
Two games (N; v) and (N;w) are strategically equivalent if there exists Alfa > 0 and Beta in |R^n such
that for all C SUB N w(C) = Alfa *v(C) + Beta* (C) = Alfa*v(C) + sum(i in C) Beta i
(SUB bedoel ik dus C is een subset van N, i in C is i is a member of C)
De vraag is nu:
Prove that strategic equivalence is an equivalence relation (i.e., it is reflexive, symmetric and
transitive).
Ik snap onder het mom van dat er een logische relatie is onderling, dat w(C) -> w(C), en als symmetrisch is dat daaruit transitiviteit volgt, maar hoe ik dit in duidelijke taal neerknal is een ander verhaal. Met mijn beknopte en half vergeten logica kennis weet ik enkel enigszins iets over p-morfismes en dat ze dezelfde eigenschappen hebben in zo'n geval. Maar of dit vergelijkbaar is?
Iemand die me in een richting kan wijzen? Alvast bedankt (weer verder gaat huiswerken)
Intro:
Two games (N; v) and (N;w) are strategically equivalent if there exists Alfa > 0 and Beta in |R^n such
that for all C SUB N w(C) = Alfa *v(C) + Beta* (C) = Alfa*v(C) + sum(i in C) Beta i
(SUB bedoel ik dus C is een subset van N, i in C is i is a member of C)
De vraag is nu:
Prove that strategic equivalence is an equivalence relation (i.e., it is reflexive, symmetric and
transitive).
Ik snap onder het mom van dat er een logische relatie is onderling, dat w(C) -> w(C), en als symmetrisch is dat daaruit transitiviteit volgt, maar hoe ik dit in duidelijke taal neerknal is een ander verhaal. Met mijn beknopte en half vergeten logica kennis weet ik enkel enigszins iets over p-morfismes en dat ze dezelfde eigenschappen hebben in zo'n geval. Maar of dit vergelijkbaar is?
Iemand die me in een richting kan wijzen? Alvast bedankt (weer verder gaat huiswerken)
Student in Tilburg?
Ik zal een eigenschap voordoen, dan kun je de andere twee zelf.
Reflexive: (N,v) is strategisch equivalent met (N,v) omdat dit direct volgt uit de definitie met alpha=1 en beta=0.
Symmetric: Als (N,v) equivalent is aan (N,w) dan geldt ...., nu geldt ook dat (N,w) equivalent is aan (N,v) omdat ....
Ik zal een eigenschap voordoen, dan kun je de andere twee zelf.
Reflexive: (N,v) is strategisch equivalent met (N,v) omdat dit direct volgt uit de definitie met alpha=1 en beta=0.
Symmetric: Als (N,v) equivalent is aan (N,w) dan geldt ...., nu geldt ook dat (N,w) equivalent is aan (N,v) omdat ....
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Nee Amsterdam, volg cooperative games aan de UvA (er is geen boek, slides vertelt hier niks over en de leraar is onduidelijk 
)
Hartstikke bedankt, dat is een goeie ogenopener.
Me bedenksel voortgebouwd op je eye opener:
Symmetrie met dezelfde waarden voor alfa/beta. Uit reflexiviteit en symmetrie volgt transiviteit. Wat weer op neer komt dat de relatie equivalent is.
[ Bericht 27% gewijzigd door koffiegast op 21-02-2010 02:37:59 ]
)Hartstikke bedankt, dat is een goeie ogenopener.
Me bedenksel voortgebouwd op je eye opener:
Symmetrie met dezelfde waarden voor alfa/beta. Uit reflexiviteit en symmetrie volgt transiviteit. Wat weer op neer komt dat de relatie equivalent is.
[ Bericht 27% gewijzigd door koffiegast op 21-02-2010 02:37:59 ]
Ik moet aan de hand van de delta-epsilon definitie van een limiet bewijzen dat een limiet niet bestaat. Daarvoor wil ik de negatie van de eps-delta definitie gebruiken. Als ik het goed heb luidt deze als volgt:
De limiet van f in a bestaat niet als er voor een zekere
een positief reëel getal 
bestaat zodat de volgende implicatie niet waar is: 
en
.
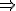
Klopt dit?
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:38:46 ]
De limiet van f in a bestaat niet als er voor een zekere
Klopt dit?
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:38:46 ]
Zeker weten? Het klinkt namelijk als een soort van instinker.quote:
[..]
Wel, bijvoorbeeld iets als ab{c,d}bba.
Nee.quote:
Symmetrie met dezelfde waarden voor alfa/beta.
Nee.quote:Uit reflexiviteit en symmetrie volgt transiviteit.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Nee, er moet een eps>0 bestaan zodanig dat er geen delta>0 bestaat zodanig dat de implicatie waar is.quote:
Ik moet aan de hand van de delta-epsilon definitie van een limiet bewijzen dat een limiet niet bestaat. Daarvoor wil ik de negatie van de eps-delta definitie gebruiken. Als ik het goed heb luidt deze als volgt:
De limiet van f in a bestaat niet als er voor een zekere [ afbeelding ] een positief reëel getal [ afbeelding ]bestaat zodat de volgende implicatie niet waar is: [ afbeelding ] en[ afbeelding ] [ afbeelding ] [ afbeelding ].
Klopt dit?
[ Bericht 3% gewijzigd door GlowMouse op 21-02-2010 16:51:47 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ja.quote:
[..]
Zeker weten? Het klinkt namelijk als een soort van instinker.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
