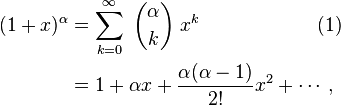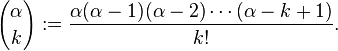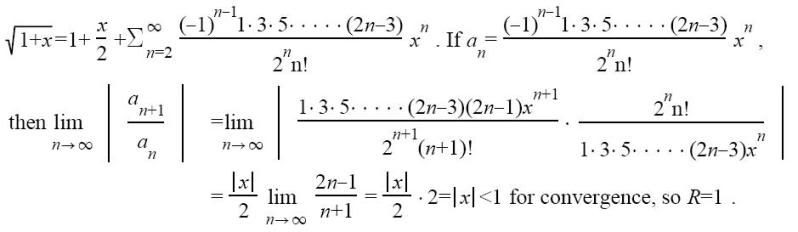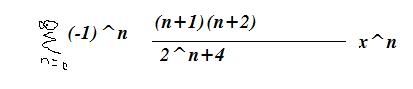SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Je hebt je uploadicon nog niet aangepast en je webicon is nu te groot natuurlijk. Gebruik dan liever dit:
Maar, los daarvan, het is een typisch voorbeeld van Islamitische ornamentiek om een vlak te versieren met regelmatige patronen (die na rotatie of spiegeling hetzelfde blijven). De indeling ‘p3’ is wiskundig, in het Alhambra vind je alle 17 indelingen al.
Ook de Nederlandse artiest Escher die bekend is om z’n patronen en indelingen heeft in het Alhambra veel inspiratie opgedaan.
Ze gebruikten uiteraard zulke geometrische versieringen i.v.m. met het taboe op afbeeldingen van levende wezens, maar dat hoef ik jou denk ik niet te vertellen.
Maar, los daarvan, het is een typisch voorbeeld van Islamitische ornamentiek om een vlak te versieren met regelmatige patronen (die na rotatie of spiegeling hetzelfde blijven). De indeling ‘p3’ is wiskundig, in het Alhambra vind je alle 17 indelingen al.
Ook de Nederlandse artiest Escher die bekend is om z’n patronen en indelingen heeft in het Alhambra veel inspiratie opgedaan.
Ze gebruikten uiteraard zulke geometrische versieringen i.v.m. met het taboe op afbeeldingen van levende wezens, maar dat hoef ik jou denk ik niet te vertellen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Jan van de Craats is een KONING! Hij is echt de leraar der leraren bij ons in de klas hahhaa. Je icon is een kruisje bij mij??
Edit: nu niet meer
Edit: nu niet meer
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Nu nog je uploadicon aanpassen!
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Hoi,
Ik ben bezig met de afgeleide bepalen, differentiëren, maar het lukt niet helemaal.
Kan iemand mij uitleggen welke stappen je neemt om bijvoorbeeld: f(x)= (x^2 + 2x)(3x + 5) op te lossen?
Alvast bedankt!
Ik ben bezig met de afgeleide bepalen, differentiëren, maar het lukt niet helemaal.
Kan iemand mij uitleggen welke stappen je neemt om bijvoorbeeld: f(x)= (x^2 + 2x)(3x + 5) op te lossen?
Alvast bedankt!
Heb je de productregel al gehad?quote:Op maandag 28 december 2009 14:20 schreef evelien89 het volgende:
Hoi,
Ik ben bezig met de afgeleide bepalen, differentiëren, maar het lukt niet helemaal.
Kan iemand mij uitleggen welke stappen je neemt om bijvoorbeeld: f(x)= (x^2 + 2x)(3x + 5) op te lossen?
Alvast bedankt!
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
=3x³+11x²+10x
en dat afleiden gaat vanzelf.
Je kan het met de productformule, maar ik denk dat dit eenvoudiger is.
en dat afleiden gaat vanzelf.
Je kan het met de productformule, maar ik denk dat dit eenvoudiger is.
Dan zou ik gewoon, wat Beregd ook zegt, de haakjes wegwerken (dan kom je op wat hij zegt als het goed is) en dan afleiden. Lukt dat?quote:
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
quote:Op maandag 28 december 2009 14:23 schreef Beregd het volgende:
=3x³+11x²+10x
en dat afleiden gaat vanzelf.
Je kan het met de productformule, maar ik denk dat dit eenvoudiger is.
hoe kom je bij 11x^2, ik kwam uit op 11x^4?
hoe dat?quote:Op maandag 28 december 2009 14:36 schreef evelien89 het volgende:
[..]
hoe kom je bij 11x^2, ik kwam uit op 11x^4?
de exponenten mag je niet optellen!quote:
als je niet inziet waarom, moet je x maar eens vervangen door 2 of 3 bvb.
owja, ik zie het nu ook.
Nog eentje: y = 5x2 + 2x + 1 → y' = 10x + 2
Dat eerste deel is helder, ik snap alleen niet waarom het '+2' op het eind is.
Nog eentje: y = 5x2 + 2x + 1 → y' = 10x + 2
Dat eerste deel is helder, ik snap alleen niet waarom het '+2' op het eind is.
Je hebt nu als het goed is de haakjes weggewerkt van die eerste, maar heb je ook de afgeleide al bepaald?
Zo ja, wat kreeg je eruit?
Zo ja, wat kreeg je eruit?
Dat komt van 2x, als je dat afleidt krijg je 2.quote:
owja, ik zie het nu ook.
Nog eentje: y = 5x2 + 2x + 1 → y' = 10x + 2
Dat eerste deel is helder, ik snap alleen niet waarom het '+2' op het eind is.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
en die +1 dan? Moet je die dan weglaten?quote:Op maandag 28 december 2009 15:15 schreef Iblis het volgende:
[..]
Dat komt van 2x, als je dat afleidt krijg je 2.
De afgeleide van een constante is 0.quote:Op maandag 28 december 2009 15:35 schreef evelien89 het volgende:
[..]
en die +1 dan? Moet je die dan weglaten?
De afgeleide kan je zien als de helling. Als je de grafiek van bijvoorbeeld y=3 tekent, dan heeft ie een helling van 0. Daarom is het ook in te zien dat y'=0 .
Ik heb er weer eentje gevonden waarvan mijn antwoord verschilt met het antwoordenboekje.
(5x + 3) (x^2 + 3). Ik kwam uit op: 16x + 15. Wat doe ik fout?
(5x + 3) (x^2 + 3). Ik kwam uit op: 16x + 15. Wat doe ik fout?
Brontosaurussen: Ik moet : Use the binominal series to expand the fucntion as a power series. State the radius of convergence. Calculus deel 6. 11.10 vraag 28.
: (1-x)2/3
Aangezien ik hier geen uitwerkingen van heb, en er in Calculus geen antwoord staat en ik er niet uitkom graag hulp. Tot zover heb ik dit al gedaan:
f(x) = (1-x)2/3
f (0) = 1
f '(x) = -2/3 (1-x)-1/3
f ' (0) = 2/3
f '' (x) = -2/9(1-x)-4/3
f '' (0) = 2/9
f ''' (x) = 8/27(1-x)-7/3
f ''' (0) = 8/27
f '''' (x) = 56/81(1-x)-10/3
f ''''(0) = 58/81
Daarmee ga ik nu f (n)(0) bepalen:
= ...... / 3n
Waar de puntjes staan heb ik nog niets kunnen bedenken. Verder zou het kunnen dat ik geen altererende iets heb, en dat dat wel hoort etc.
Ik wil die f^n(0) weten om dit in te vullen:
sommatieteken: (f^n(0)/ n!) * x^n
Daarna kan ik dit weer gebruiken om het in een taylorreeks te gieten. Mar goed wie helpt me uit de brand. Ik vind dit hoofdstuk sowieso een en al vaagheid. Elke keer gebruiken ze opeens een andere methode en manier.
: (1-x)2/3
Aangezien ik hier geen uitwerkingen van heb, en er in Calculus geen antwoord staat en ik er niet uitkom graag hulp. Tot zover heb ik dit al gedaan:
f(x) = (1-x)2/3
f (0) = 1
f '(x) = -2/3 (1-x)-1/3
f ' (0) = 2/3
f '' (x) = -2/9(1-x)-4/3
f '' (0) = 2/9
f ''' (x) = 8/27(1-x)-7/3
f ''' (0) = 8/27
f '''' (x) = 56/81(1-x)-10/3
f ''''(0) = 58/81
Daarmee ga ik nu f (n)(0) bepalen:
= ...... / 3n
Waar de puntjes staan heb ik nog niets kunnen bedenken. Verder zou het kunnen dat ik geen altererende iets heb, en dat dat wel hoort etc.
Ik wil die f^n(0) weten om dit in te vullen:
sommatieteken: (f^n(0)/ n!) * x^n
Daarna kan ik dit weer gebruiken om het in een taylorreeks te gieten. Mar goed wie helpt me uit de brand. Ik vind dit hoofdstuk sowieso een en al vaagheid. Elke keer gebruiken ze opeens een andere methode en manier.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Heb je Binomial series al bekeken?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Dus op een of andere manier , schrijf ik mijn gegeven om tot iets waarbij ik de vorm (1-alfa)^k krijg. Waardoor ik sommatieteken: (alfa k ) x^n krijg. en dan de standaard reeks kan invullen:
Daarna moet ik op een of andere manier van die reeks een powerreeks maken?
Daarna moet ik op een of andere manier van die reeks een powerreeks maken?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Zoals er staat, geldt het voor elke α, of het nou geheel of reëel (of zelfs complex) is, dat zegt GlowMouse’ link ook. Dus in jouw geval krijg je:
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
waarbij je gelijk ziet dat het hele gedoe met binomiaalcoefficienten zinloos is omdat je er met differentieren ook al op uitkwam
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Op zich, maar als de vraag expliciet zo gesteld wordt.quote:
waarbij je gelijk ziet dat het hele gedoe met binomiaalcoefficienten zinloos is omdat je er met differentieren ook al op uitkwam
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Persoonlijk vind ik de methode met binomiaalcoefficienten een stuk strakker dan al dat gedifferentieer.
Kijk deze heb ik ook gewoon normaal op mijn formuleblad staan. Ik moet het nu specifiek doen met binominale etc. Maar het is zo vaag. Bijvoorbeeld deze som:quote:Op maandag 28 december 2009 19:47 schreef GlowMouse het volgende:
waarbij je gelijk ziet dat het hele gedoe met binomiaalcoefficienten zinloos is omdat je er met differentieren ook al op uitkwam
wortel (1+x) ==> (1+x)1/2
Die kun je dan ook zo invullen zou je zeggen in dat formaatje, maar daar komt toch echt iets anders uit bij de antwoorden. In de uitwerkingen doen ze dit:
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Die 2n n! krijg je dus niet bij het "gewoon" invullen van die standaard vorm gegeven door Ibo.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Wel. Je krijgt in de teller 1/2·-1/2·-3/2·-5/2··· in de teller, als je die samenvoegt krijg je 2n, die dan naar de noemer verhuist.quote:
Die 2n n! krijg je dus niet bij het "gewoon" invullen van die standaard vorm gegeven door Ibo.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ja en die moet je weer omschrijven tot een sommatieteken toch?quote:Op maandag 28 december 2009 19:45 schreef Iblis het volgende:
Zoals er staat, geldt het voor elke α, of het nou geheel of reëel (of zelfs complex) is, dat zegt GlowMouse’ link ook. Dus in jouw geval krijg je:
[ afbeelding ]
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Ik vermoed dat je wat anders bedoelt en dat dat niet juist is.quote:
[..]
Ja en die moet je weer omschrijven tot een sommatieteken toch?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Neem nou als voorbeeld 1/(2+3)3 ...quote:Op maandag 28 december 2009 19:45 schreef Iblis het volgende:
Zoals er staat, geldt het voor elke α, of het nou geheel of reëel (of zelfs complex) is, dat zegt GlowMouse’ link ook. Dus in jouw geval krijg je:
[ afbeelding ]
In standaardvorm met jouw dingetje, krijg je dan:
k = -3
Dus 1+3x + (12/2!)*x2 +( -60/3!)*x3 etc. etc. , maar hierna moet er nog iets zijn, omdat ! het boek dan opeens komt met (ja het is paint sorry):
Goed ik kan begrijpen waarom er (n+1) (n+2) staat, (alhoewel ik daar zelf echt niet op zou komen), maar waarom die 2^n+4 in de noemer... en er is zelfs geen faculteit meer!
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Die k loopt van 0 t/m ∞.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Het het precies zo ingevuld als hier (op dezer maniier):quote:Op maandag 28 december 2009 22:32 schreef Iblis het volgende:
Die k loopt van 0 t/m ∞.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Sorry, ik volg echt niet wat je doet.
Je schreef 1/(2 + 3)3, dat lijkt me niet correct vanwege missende x. Wat is de juist formule?
Je schreef 1/(2 + 3)3, dat lijkt me niet correct vanwege missende x. Wat is de juist formule?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
1/ (2+x)3quote:Op maandag 28 december 2009 22:45 schreef Iblis het volgende:
Sorry, ik volg echt niet wat je doet.
Je schreef 1/(2 + 3)3, dat lijkt me niet correct vanwege missende x. Wat is de juist formule?
Oke werk die maar zo uit met binominale dat je tot het antwoord komt die ik heb gepaint. Stap voor stap als het kan. Ik ben echt aan het einde van mijn latijn. Ik zie het gewoon niet meer.
(dit is het antwoord van het boek. )
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Oké, maar je hebt de formule voor (1 + x)α, hoe wilde je jouw geval daarin omtoveren? Er is ook wel een ontwikkeling voor (c + x)α te geven, want die heb je nodig.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Die twee er uit halen waardoor je : 2* (1 + x/2) -3 krijgt toch?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Dat dacht ik niet.quote:
Die twee er uit halen waardoor je : 2* (1 + x/2) -3 krijgt toch?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
