W&T Wetenschap & Technologie
Een plek om te discussiëren over wetenschappelijke onderwerpen, wetenschappelijke problemen, technologische projecten en grootse uitvindingen.
Geweldig spannend artikel om te lezen.
Zou dit de missing link zijn tussen Einstein/Newton's zwaartekrachtstheorieën en de modellen van de quantumfysica?
http://www.scientificblog(...)graphic_hot_horizons
Zou dit de missing link zijn tussen Einstein/Newton's zwaartekrachtstheorieën en de modellen van de quantumfysica?
http://www.scientificblog(...)graphic_hot_horizons
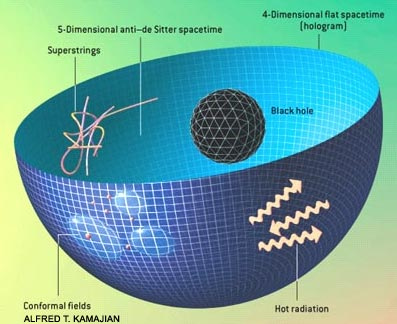
Het holografische principe is inderdaad een waanzinnig interessant onderzoeksgebied, en hier kwamen vorige week ook al de eerste berichten binnen over Verlinde's presentatie van zijn nieuwbakken theorie. Ik doe zelf gerelateerd onderzoek naar dit soort zaken, dus laat me een poging doen om mijn beperkte begrip van dit onderwerp hier neer te zetten. De gebruikelijke reviews gaan vaak al redelijk vlot de diepte in met snaartheorie, maar het uiteindelijke principe is niet verschrikkelijk ingewikkeld.
De meeste mensen hier die geinteresseerd zijn in dit soort fysica zullen ongetwijfeld weten dat Hawking in de jaren 70 aantoonde dat zwarte gaten heel gestaag deeltjes uitzenden. Dit blijkt uit een perturbatieve berekening waarin je kwantumveldentheorie en algemene relativiteit probeert te verbinden. Dit kan alleen perturbatief, omdat we geen volledige theorie van kwantumgravitatie hebben.
Bekenstein vond dit resultaat niet zo gek; hij had namelijk al een tijdje eerder beredeneerd dat een zwart gat een entropie kon hebben. De bewegingsvergelijkingen van zwarte gaten zien er qua vorm precies zo uit als de thermodynamische vergelijkingen, waarin de verschillende aspecten van zwarte gaten zich gedragen alsof ze thermodynamische grootheden zijn! De overeenkomsten zijn ongeveer als volgt:
Zwart gat - Thermodynamisch systeem
Oppervlaktezwaartekracht - temperatuur
Waarnemershorizon - entropie
Massa - energie
Dit zou natuurlijk toeval kunnen zijn, maar Hawkings bevinding laat ons denken dat dit waarschijnlijk meer is dan slechts toeval. Het oppervlakte van de waarnemershorizon geeft volgens Bekenstein een maat voor de entropie, en die kun je op verschillende manieren uitrekenen.
In de thermodynamica kun je entropie op twee verschillende manieren bekijken: macroscopisch en microscopisch. Macroscopisch is de entropie S een grootheid die afhangt van je externe parameters, bijvoorbeeld de energie E, het aantal deeltjes N en de druk P. Microscopisch is de entropie ruwweg het aantal configuraties van je systeem, en die moet je kwantummechanisch tellen.
Nu zou je dus kunnen zeggen dat de oppervlakte van de waarnemershorizon een macroscopische beschrijving is van je entropie. De vraag is: kun je ook een microscopische beschrijving geven? Dit blijkt erg ingewikkeld te zijn, ook weer omdat we zwaartekracht niet kwantummechanisch kunnen beschrijven. Vanuit snaartheorie kan men alleen van een bepaalde klasse van zwarte gaten de entropie microscopisch verklaren, namelijk van extremale zwarte gaten .
Nu zal iemand met wat kennis van thermodynamica dit verhaal eigenaardig vinden. Want in de thermodynamica schaalt de entropie met het volume van je systeem; entropie is een extensieve grootheid. Als je het volume V x keer zo groot maakt, dan wordt de entropie ook x maal zo groot. Bij een zwart gat schaalt de entropie echter met het oppervlak! Da's apart. Nou is een zwart gat sowieso een apart verschijnsel; het is in zekere zin "de meest pure vorm van zwaartekracht" wat we kennen. De entropie vertelt je iets over de configuratie van je systeem, en dus over je vrijheidsgraden. Kan het zo zijn dat bij zwaartekracht in D ruimtetijd dimensies de vrijheidsgraden eigenlijk kunnen worden beschreven in D-1 ruimtetijd dimensies?
Dit is de motivatie voor het zogenaamde holografische principe. Het holografische principe zegt eigenlijk dat een bepaalde zwaartekrachtstheorie in D dimensies "duaal is" aan een kwantumveldentheorie in D-1 dimensies. Een kwantumveldentheorie kun je ook lezen als "kwantummechanische theorie", voor als je het verschil niet kent. Deze kwantumveldentheorie blijkt op de rand van de ruimtetijd te leven waarin je je zwaartekrachtstheorie hebt geformuleerd.
Om er een plaatje van te maken: bekijk een zwaartekrachtstheorie in een ruimtetijd die je als een bol tekent, dan is deze theorie "duaal" aan een kwantumveldentheorie op het oppervlakte van deze bol. "Duaal" betekent dat ze in feite precies dezelfde natuurkunde beschrijven. Een simpel voorbeeldje is elektromagnetisme. Elektriciteit en magnetisme zijn twee duale verschijnselen; een elektrisch veld kan voor een andere waarnemer een magnetisch veld zijn. Dezelfde fysica, maar twee verschillende beschrijvingen. Het fantastische aan deze boven beschreven holografie is echter dat we het nu hebben over een dualiteit tussen twee theorieën die op het eerste gezicht compleet anders zijn!
Nou wordt het wat technisch. Deze kwantumveldentheorie blijkt een conformale veldentheorie te zijn, een theorie met schaalinvariantie. Vanuit renormalizatiegroepen weet je dat je deze conformale veldentheorie kunt beschrijven met een dimensie extra, waarin deze extra dimensie de energieschaal voorstelt. Je kunt met alle symmetrieën nu voor de gein es proberen een metriek op te schrijven voor de Minkowski ruimtetijd waarin deze conformale veldentheorie zich bevindt met deze extra dimensie. De metriek die je krijgt is een hele bekende uit snaartheorie: een zogenaamde "anti de Sitter metriek", die de maximaal symmetrische hyperbolische ruimte beschrijft met constante kromming. De zwaartekrachtstheorie die duaal is aan deze conformale kwantumveldentheorie is dan ook een zwaartekrachtstheorie geformuleerd op een anti de Sitter ruimtetijd.
Je kunt nu als het ware een kookboek opschrijven voor de verschillende correspondenties in de conformale theorie en de zwaartekrachtstheorie. Het is misschien wel belangrijk om te zeggen dat deze dualiteit, die vaak "AdS/CFT" wordt genoemd niet in zijn algemeenheid bewezen is. Dat komt ook omdat ze volgens mij van nature via snaartheorie is geponeerd door Maldacena, en men simpelweg niet weet wat snaartheorie nu precies inhoudt.
Misschien dat sommige mensen hier wat wijzer uit kunnen worden
De meeste mensen hier die geinteresseerd zijn in dit soort fysica zullen ongetwijfeld weten dat Hawking in de jaren 70 aantoonde dat zwarte gaten heel gestaag deeltjes uitzenden. Dit blijkt uit een perturbatieve berekening waarin je kwantumveldentheorie en algemene relativiteit probeert te verbinden. Dit kan alleen perturbatief, omdat we geen volledige theorie van kwantumgravitatie hebben.
Bekenstein vond dit resultaat niet zo gek; hij had namelijk al een tijdje eerder beredeneerd dat een zwart gat een entropie kon hebben. De bewegingsvergelijkingen van zwarte gaten zien er qua vorm precies zo uit als de thermodynamische vergelijkingen, waarin de verschillende aspecten van zwarte gaten zich gedragen alsof ze thermodynamische grootheden zijn! De overeenkomsten zijn ongeveer als volgt:
Zwart gat - Thermodynamisch systeem
Oppervlaktezwaartekracht - temperatuur
Waarnemershorizon - entropie
Massa - energie
Dit zou natuurlijk toeval kunnen zijn, maar Hawkings bevinding laat ons denken dat dit waarschijnlijk meer is dan slechts toeval. Het oppervlakte van de waarnemershorizon geeft volgens Bekenstein een maat voor de entropie, en die kun je op verschillende manieren uitrekenen.
In de thermodynamica kun je entropie op twee verschillende manieren bekijken: macroscopisch en microscopisch. Macroscopisch is de entropie S een grootheid die afhangt van je externe parameters, bijvoorbeeld de energie E, het aantal deeltjes N en de druk P. Microscopisch is de entropie ruwweg het aantal configuraties van je systeem, en die moet je kwantummechanisch tellen.
Nu zou je dus kunnen zeggen dat de oppervlakte van de waarnemershorizon een macroscopische beschrijving is van je entropie. De vraag is: kun je ook een microscopische beschrijving geven? Dit blijkt erg ingewikkeld te zijn, ook weer omdat we zwaartekracht niet kwantummechanisch kunnen beschrijven. Vanuit snaartheorie kan men alleen van een bepaalde klasse van zwarte gaten de entropie microscopisch verklaren, namelijk van extremale zwarte gaten .
Nu zal iemand met wat kennis van thermodynamica dit verhaal eigenaardig vinden. Want in de thermodynamica schaalt de entropie met het volume van je systeem; entropie is een extensieve grootheid. Als je het volume V x keer zo groot maakt, dan wordt de entropie ook x maal zo groot. Bij een zwart gat schaalt de entropie echter met het oppervlak! Da's apart. Nou is een zwart gat sowieso een apart verschijnsel; het is in zekere zin "de meest pure vorm van zwaartekracht" wat we kennen. De entropie vertelt je iets over de configuratie van je systeem, en dus over je vrijheidsgraden. Kan het zo zijn dat bij zwaartekracht in D ruimtetijd dimensies de vrijheidsgraden eigenlijk kunnen worden beschreven in D-1 ruimtetijd dimensies?
Dit is de motivatie voor het zogenaamde holografische principe. Het holografische principe zegt eigenlijk dat een bepaalde zwaartekrachtstheorie in D dimensies "duaal is" aan een kwantumveldentheorie in D-1 dimensies. Een kwantumveldentheorie kun je ook lezen als "kwantummechanische theorie", voor als je het verschil niet kent. Deze kwantumveldentheorie blijkt op de rand van de ruimtetijd te leven waarin je je zwaartekrachtstheorie hebt geformuleerd.
Om er een plaatje van te maken: bekijk een zwaartekrachtstheorie in een ruimtetijd die je als een bol tekent, dan is deze theorie "duaal" aan een kwantumveldentheorie op het oppervlakte van deze bol. "Duaal" betekent dat ze in feite precies dezelfde natuurkunde beschrijven. Een simpel voorbeeldje is elektromagnetisme. Elektriciteit en magnetisme zijn twee duale verschijnselen; een elektrisch veld kan voor een andere waarnemer een magnetisch veld zijn. Dezelfde fysica, maar twee verschillende beschrijvingen. Het fantastische aan deze boven beschreven holografie is echter dat we het nu hebben over een dualiteit tussen twee theorieën die op het eerste gezicht compleet anders zijn!
Nou wordt het wat technisch. Deze kwantumveldentheorie blijkt een conformale veldentheorie te zijn, een theorie met schaalinvariantie. Vanuit renormalizatiegroepen weet je dat je deze conformale veldentheorie kunt beschrijven met een dimensie extra, waarin deze extra dimensie de energieschaal voorstelt. Je kunt met alle symmetrieën nu voor de gein es proberen een metriek op te schrijven voor de Minkowski ruimtetijd waarin deze conformale veldentheorie zich bevindt met deze extra dimensie. De metriek die je krijgt is een hele bekende uit snaartheorie: een zogenaamde "anti de Sitter metriek", die de maximaal symmetrische hyperbolische ruimte beschrijft met constante kromming. De zwaartekrachtstheorie die duaal is aan deze conformale kwantumveldentheorie is dan ook een zwaartekrachtstheorie geformuleerd op een anti de Sitter ruimtetijd.
Je kunt nu als het ware een kookboek opschrijven voor de verschillende correspondenties in de conformale theorie en de zwaartekrachtstheorie. Het is misschien wel belangrijk om te zeggen dat deze dualiteit, die vaak "AdS/CFT" wordt genoemd niet in zijn algemeenheid bewezen is. Dat komt ook omdat ze volgens mij van nature via snaartheorie is geponeerd door Maldacena, en men simpelweg niet weet wat snaartheorie nu precies inhoudt.
Misschien dat sommige mensen hier wat wijzer uit kunnen worden
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Ik heb ook nog even de afleiding op de blog bekeken, en ik moet zeggen dat het best wel curieus is. Zoals de schrijver ook zegt: je wilt natuurlijk op deze manier de Einsteinvergelijkingen kunnen afleiden, maar er zijn al meerdere artikelen hierover geschreven, waaronder de link in de tweede post een mooie review van geeft.
Een mooi stukje leesvoer voor in de Kerstvakantie!
Een mooi stukje leesvoer voor in de Kerstvakantie!
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Dank voor je heldere uitleg, Haushofer. Het blijft indrukwekkend hoe jij telkens opnieuw, uitermate complexe materie in (voor mij bijna) volgbare zinnen weet te transformeren. 
Er lijkt iets te broeien in wetenschapsland (ik las nota bene over de presentatie van Verlinde op een forum over religie...) en het zou me niets verbazen als Verlinde echt een doorbraak te pakken heeft.
P.S.
Quote van een andere site: "De laatste maanden werkte hij aan een theorie waarin de aantrekking tussen twee massa’s vanzelf ontstaat door informatieverschillen in de ruimte tussen de massa’s en die daarbuiten."
Dit is natuurlijk populair gezegd, maar wordt hier met informatie verwezen naar entropie?
Er lijkt iets te broeien in wetenschapsland (ik las nota bene over de presentatie van Verlinde op een forum over religie...) en het zou me niets verbazen als Verlinde echt een doorbraak te pakken heeft.
P.S.
Quote van een andere site: "De laatste maanden werkte hij aan een theorie waarin de aantrekking tussen twee massa’s vanzelf ontstaat door informatieverschillen in de ruimte tussen de massa’s en die daarbuiten."
Dit is natuurlijk populair gezegd, maar wordt hier met informatie verwezen naar entropie?
Ja, in feite wel. Ik zal proberen om het idee te schetsen, iets wat de persoon op die blog ook heeft gedaan.quote:Op dinsdag 15 december 2009 18:14 schreef Agno het volgende:
Dank voor je heldere uitleg, Haushofer. Het blijft indrukwekkend hoe jij telkens opnieuw, uitermate complexe materie in (voor mij bijna) volgbare zinnen weet te transformeren.
Er lijkt iets te broeien in wetenschapsland (ik las nota bene over de presentatie van Verlinde op een forum over religie...) en het zou me niets verbazen als Verlinde echt een doorbraak te pakken heeft.
P.S.
Quote van een andere site: "De laatste maanden werkte hij aan een theorie waarin de aantrekking tussen twee massa’s vanzelf ontstaat door informatieverschillen in de ruimte tussen de massa’s en die daarbuiten."
Dit is natuurlijk populair gezegd, maar wordt hier met informatie verwezen naar entropie?
Neem een massa M in een ruimte. Uit mijn eerdere post is het hopelijk duidelijk geworden dat de vrijheidsgraden van dit systeem gevonden kunnen worden op de rand van deze ruimte. Dus neem es een bol met straal R rondom deze massa. Het holografische principe stelt dat we de entropie, en dus de "informatie" van dit systeem op de rand van deze bol kunnen beschrijven; we hebben niet het volume van de bol nodig zoals je klassiek thermodynamisch zou verwachten.
Die bol heeft een oppervlakte 4*pi*R2. Als je een oppervlakte Abit per "bit informatie" toedeelt, dan zou je ruwweg kunnen zeggen dat het maximale aantal bits op het oppervlak, en dus de maximale informatie van je systeem M, gegeven wordt door
N = 4*pi*R2/Abit
Nou is er een equipartitie theorema in de statistische fysica die stelt dat elke vrijheidsgraad in een thermodynamisch systeem correspondeert met een energie 1/2k*T, waarbij k de Boltzmannconstante is. Die "bits" corresponderen met informatie over het systeem M, wat weer correspondeert met de entropie, wat weer correspondeert met de vrijheidsgraden. Je zou dus ruwweg kunnen stellen dat
1/2 k*T*N = Mc2
Nu heb je dus een temperatuur te pakken. Bij mensen die veel met algemene relativiteit doen zou er nu een belletje kunnen gaan rinkelen. Het zogenaamde Unruh effect stelt dat een versnellende waarnemer met versnelling a in een Minkowski ruimte het vacuum zal ervaren als een hittebad met een bepaalde temperatuur T. De relatie is dat
T = h*a/2*pi*c*k
Dit fenomeen kun je verklaren via analytische continuaties, op eenzelfde manier als je de Hawkingtemperatuur van een Schwarzschild zwart gat via een analytische continuatie van je Euclidische tijdscoordinaat uitvoert; de periodiciteit van deze coordinaat, die je invoert om een fysische singulariteit te omzeilen omdat je weet dat je slechts met een coordinaatsingulariteit hebt te maken, laat een identificatie met een partitiefunctie toe.
Dan is het een kwestie van inpluggen en een relatie krijgen in de vorm van
a = C*M/R2
De C is een constante die afhangt van Abit. Je zou hiervoor de Planckoppervlakte voor kunnen gebruiken, en dan zie je dat C wel heel mooi naar de gravitatieconstante G gaat, ware het niet dat dat Planckoppervlak al van G afhangt; Planckeenheden zijn simpelweg grootheden geconstrueerd uit h,c en G.
Het blijft al met al een leuk berekeningetje
[ Bericht 0% gewijzigd door Haushofer op 15-12-2009 19:03:49 ]
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Ben nogal visueel ingesteld, dus daarom gelijk maar even een plaatje gemaakt
Klopt dit een beetje?
[ Bericht 1% gewijzigd door Agno op 16-12-2009 11:40:47 ]
Klopt dit een beetje?
[ Bericht 1% gewijzigd door Agno op 16-12-2009 11:40:47 ]
Uit het Volkskrantartikel:
(...)
MEN NEME EEN ZWART GAT EN EEN HOLOGRAM
Erik Verlindes afleiding van Newtons klassieke mechanica berust op een al ouder idee van zijn leermeester en Nobelprijswinnaar (1999) Gerard ’t Hooft: alle informatie over alle deeltjes in een fysisch systeem wordt als in een hologram opgeslagen op een bol eromheen. Die voorstelling raakt aan theorieën van Stephen Hawking over de oppervlakken van zwarte gaten.
Men neme een zwart gat, een zo grote massa dat zelfs licht er niet aan kan ontsnappen als het een bepaalde horizon overschrijdt. Volgens de theorieën van Hawking heeft die bolvormige horizon een oppervlak dat evenredig is met de hoeveelheid informatie die in het zwarte gat is verdwenen. Die horizon is echter niet helemaal mathematisch glad; er is een minimale onzekerheid over waar deze zich bevindt. Dat komt omdat in de quantumwereld niets exact vaststaat. Die onzekerheid, zo liet Hawking in een beroemd geworden stelling zien, betekent dat zwarte gaten een temperatuur hebben en dus ook energie uitstralen.
Volgens ’t Hooft is op dezelfde manier rond iedere grote massa M een soort hologram te bedenken, een scherm waarop alle informatie over de hele inhoud is opgeslagen in de vorm van bits. De energie binnen de bol is netjes verdeeld over de bits op het scherm. Daarmee is ook aan het denkbeeldige holografische scherm een temperatuur toe te kennen. Die op zichzelf denkbeeldige temperatuur is volgens Erik Verlinde de sleutel tot de zwaartekracht die een massa m van massa M ondergaat.
Als een deeltje met een massa m net van de ene kant van het denkbeeldige scherm naar de andere wordt gebracht, verandert de informatie-inhoud van de bol met één bit. Die verandering maal de temperatuur van het scherm is volgens Verlinde de energieverandering van het systeem. Die energieverandering moet worden opgebracht tijdens de verplaatsing. Wie het deeltje wil verzetten, voelt dit altijd als kracht richting massa M.
Tot zover het conceptuele verhaal, dat volledig berust op gedachten over informatie en energie binnen een fysisch systeem en wat veranderingen daarin betekenen. De crux: verplaatsen van een massa geeft informatieverandering die energie kost, wat zich uit in een aantrekkingskracht.
Verlinde combineert simpele formules voor energie, informatie-inhoud, temperatuur, oppervlakten en aantallen bits, en vindt vrijwel direct twee klassieke wetten van Newton. De eerste is de versnellingswet F = ma: kracht is massa maal versnelling a van een deeltje met massa m.
De tweede is Newtons gravitatiewet, die zegt dat massa's M en m elkaar op een afstand R aantrekken met een kracht die evenredig is met de massa's en omgekeerd evenredig met het kwadraat van de afstand.
(...)
Op de website van Verlinde staat ook een filmpje (onder "talks" en "gravitatie uit informatie").
Hij leidt dus zomaar even bottom-up Newton's wetten: F=m.a en a = (m1*m2*G)/R2 af.
http://staff.science.uva.nl/~erikv/index.html
(...)
MEN NEME EEN ZWART GAT EN EEN HOLOGRAM
Erik Verlindes afleiding van Newtons klassieke mechanica berust op een al ouder idee van zijn leermeester en Nobelprijswinnaar (1999) Gerard ’t Hooft: alle informatie over alle deeltjes in een fysisch systeem wordt als in een hologram opgeslagen op een bol eromheen. Die voorstelling raakt aan theorieën van Stephen Hawking over de oppervlakken van zwarte gaten.
Men neme een zwart gat, een zo grote massa dat zelfs licht er niet aan kan ontsnappen als het een bepaalde horizon overschrijdt. Volgens de theorieën van Hawking heeft die bolvormige horizon een oppervlak dat evenredig is met de hoeveelheid informatie die in het zwarte gat is verdwenen. Die horizon is echter niet helemaal mathematisch glad; er is een minimale onzekerheid over waar deze zich bevindt. Dat komt omdat in de quantumwereld niets exact vaststaat. Die onzekerheid, zo liet Hawking in een beroemd geworden stelling zien, betekent dat zwarte gaten een temperatuur hebben en dus ook energie uitstralen.
Volgens ’t Hooft is op dezelfde manier rond iedere grote massa M een soort hologram te bedenken, een scherm waarop alle informatie over de hele inhoud is opgeslagen in de vorm van bits. De energie binnen de bol is netjes verdeeld over de bits op het scherm. Daarmee is ook aan het denkbeeldige holografische scherm een temperatuur toe te kennen. Die op zichzelf denkbeeldige temperatuur is volgens Erik Verlinde de sleutel tot de zwaartekracht die een massa m van massa M ondergaat.
Als een deeltje met een massa m net van de ene kant van het denkbeeldige scherm naar de andere wordt gebracht, verandert de informatie-inhoud van de bol met één bit. Die verandering maal de temperatuur van het scherm is volgens Verlinde de energieverandering van het systeem. Die energieverandering moet worden opgebracht tijdens de verplaatsing. Wie het deeltje wil verzetten, voelt dit altijd als kracht richting massa M.
Tot zover het conceptuele verhaal, dat volledig berust op gedachten over informatie en energie binnen een fysisch systeem en wat veranderingen daarin betekenen. De crux: verplaatsen van een massa geeft informatieverandering die energie kost, wat zich uit in een aantrekkingskracht.
Verlinde combineert simpele formules voor energie, informatie-inhoud, temperatuur, oppervlakten en aantallen bits, en vindt vrijwel direct twee klassieke wetten van Newton. De eerste is de versnellingswet F = ma: kracht is massa maal versnelling a van een deeltje met massa m.
De tweede is Newtons gravitatiewet, die zegt dat massa's M en m elkaar op een afstand R aantrekken met een kracht die evenredig is met de massa's en omgekeerd evenredig met het kwadraat van de afstand.
(...)
Op de website van Verlinde staat ook een filmpje (onder "talks" en "gravitatie uit informatie").
Hij leidt dus zomaar even bottom-up Newton's wetten: F=m.a en a = (m1*m2*G)/R2 af.
http://staff.science.uva.nl/~erikv/index.html
Dat heb je tov gedaan!quote:Op dinsdag 15 december 2009 22:26 schreef Agno het volgende:
Ben nogal visueel ingesteld, dus daarom gelijk maar even een plaatje gemaakt
[ link | afbeelding ]
Klopt dit een beetje?
De formule van de Unruh temperatuur moet echter T= (ha)/(2*pi*c*k) zijn, waarbij h "h-streep" is. Voor de rest vat je plaatje denk ik goed samen wat het holografische principe inhoudt; dit soort plaatjes vind je wel vaker terug, bijvoorbeeld hier,
of hier,
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Leuk artikel, maar aan uitspraken als "Dat komt omdat in de quantumwereld niets exact vaststaat" stoor ik me altijd een beetje; dat laat geloven dat je in de kwantummechanica niets met willekeurige precisie kunt vaststellen.quote:
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Heb de formule gecorrigeerd (zo zie je maar weer hoe belangrijk haakjes zijn in de wiskunde...)quote:Op woensdag 16 december 2009 09:16 schreef Haushofer het volgende:
De formule van de Unruh temperatuur moet echter T= (ha)/(2*pi*c*k) zijn, waarbij h "h-streep" is.
.Weet jij ook hoe Verlinde Newton's versnellingswet F=m a uit de entropiewetten afgeleid heeft?
Verlinde moet nu alleen nog even de veldvergelijkingen van Einstein afleiden uit lokale informatieverschillen...
Volgens mij zou dat een redenatie worden als volgt:quote:Op woensdag 16 december 2009 11:49 schreef Agno het volgende:
[..]
Heb de formule gecorrigeerd (zo zie je maar weer hoe belangrijk haakjes zijn in de wiskunde...)
Weet jij ook hoe Verlinde Newton's versnellingswet F=m a uit de entropiewetten afgeleid heeft?
Verlinde moet nu alleen nog even de veldvergelijkingen van Einstein afleiden uit lokale informatieverschillen...
Je weet dat uit de thermodynamica volgt dat dE=TdS. Die dE kun je schrijven als Fdx. Als je nu voor dx de Comptongolflengte invult en de Unruh formule gebruikt, dan verkrijg je iets als
F*h/(mc) = (h*a)/(2*pi*k*c)dS
Dit is dus
F=m*a*(dS/2*pi*k),
waarbij de afleiding hout zou snijden als dS=2*pi*k. Ik moet zeggen dat de tussenstappen me niet helemaal duidelijk zijn en de motivatie ook niet, maar in die richting moet je het zoeken denk ik.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
De afleiding van het 'schoolbord' is vrij eenvoudig:quote:Op woensdag 16 december 2009 12:16 schreef Haushofer het volgende:
[..]
Volgens mij zou dat een redenatie worden als volgt:
Je weet dat uit de thermodynamica volgt dat dE=TdS. Die dE kun je schrijven als Fdx. Als je nu voor dx de Comptongolflengte invult en de Unruh formule gebruikt, dan verkrijg je iets als
F*h/(mc) = (h*a)/(2*pi*k*c)dS
Dit is dus
F=m*a*(dS/2*pi*k),
waarbij de afleiding hout zou snijden als dS=2*pi*k. Ik moet zeggen dat de tussenstappen me niet helemaal duidelijk zijn en de motivatie ook niet, maar in die richting moet je het zoeken denk ik.
F dX = T dS
dX = h/(mc)
dS = 2 pi kB (=entropie van 1 bit die "door" het holografische scherm gaat)
kB T = 1/(2 pi) x (ha)/c (= Unruh)
Dus,
F h/(mc) = (2 pi kB) x ((1/(2pi) x (ha)/c) / kB)
F = ma
Verbazingwekkend eenvoudig.
Ja, ik wacht zijn artikel ook nog even af voordat ik conclusies hier uit ga trekken.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Allemaal erg ingewikkeld. Ik wacht wel tot de documentaire uit is 
"An educated citizenry is a vital requisite for our survival as a free people."
Ja, zo is het iddquote:Op dinsdag 15 december 2009 22:26 schreef Agno het volgende:
Ben nogal visueel ingesteld, dus daarom gelijk maar even een plaatje gemaakt
[ link | afbeelding ]
Klopt dit een beetje?
Eindelijk iemand die denkt wat iedereen zegt
Mooi geschematiseerd hoor.quote:Op dinsdag 15 december 2009 22:26 schreef Agno het volgende:
Ben nogal visueel ingesteld, dus daarom gelijk maar even een plaatje gemaakt
[ link | afbeelding ]
Klopt dit een beetje?
En vandaag publiceert T. Padmanabhan vrijwel hetzelfde idee als Verlinde op arXiv:
Equipartition of energy in the horizon degrees of freedom and the emergence of gravity
Misschien leest Padmanabhan ook wel de Volkskrant
Equipartition of energy in the horizon degrees of freedom and the emergence of gravity
Misschien leest Padmanabhan ook wel de Volkskrant
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Ik zag vanochtend dat Verlinde zijn praatjes van de website heeft gehaald. Ergens vermoed ik dat Padmanabhan de boven genoemde blog heeft gelezen of er op een andere manier lucht van heeft gekregen, in sneltreinvaart het artikeltje heeft uitgepoept en Verlinde zo gescooped heeft.
Het lijkt erop dat Verlinde een elementaire fout heeft gemaakt door de publiciteit op te zoeken.
Het lijkt erop dat Verlinde een elementaire fout heeft gemaakt door de publiciteit op te zoeken.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Dat was mij ook al opgevallen. Alle filmpjes zijn van de site verdwenen. Zou wel een beetje zonde zijn van zo'n doorbraak en zeker als het via een foto van zijn werkkamer en een slim lezende natuurkundige naar Padmanabhan gelekt is.quote:Op maandag 21 december 2009 11:21 schreef Haushofer het volgende:
Ik zag vanochtend dat Verlinde zijn praatjes van de website heeft gehaald. Ergens vermoed ik dat Padmanabhan de boven genoemde blog heeft gelezen of er op een andere manier lucht van heeft gekregen, in sneltreinvaart het artikeltje heeft uitgepoept en Verlinde zo gescooped heeft.
Het lijkt erop dat Verlinde een elementaire fout heeft gemaakt door de publiciteit op te zoeken.
Maar wellicht prevaleert onze Nederlandse trots boven een eerlijk allocatie van de 'credit' voor deze doorbraak. Het verhaal kan natuurlijk ook zo zijn dat Verlinde zich baseert op een eerdere publicatie van Padmanabhan, snel de 'last loop' bedenkt en vervolgens als een speer de publiciteit gezocht heeft. We weten het niet.
De vraag over wie de 'credit' voor een wetenschappelijke doorbraak krijgt is interessant. Wat telt in de wetenschappelijke wereld: is het altijd degene die als eerste formeel publiceert of is het degene die als eerste publiek gaat? Hoe werkt bijv. zo'n Spinoza lezing? Moeten alle aanwezigen vooraf een soort non-disclosure tekenen?
P.S.
Heb het plaatje nog wat aangepast en nu ook de afleiding F=ma toegevoegd.
Nee, je hoeft niks te tekenen. Formeel geldt denk ik dat degene die als eerste publiceert de credits krijgt. Normaal gezien doen wetenschappers dat denk ik niet zo gauw, "publiek gaan" voordat ze gepubliceerd hebben. Daarom denk ik ook dat Verlinde een elementaire fout heeft gemaakt en misschien eerst de zaak beter had moeten uitdenken en opschrijven in een artikel alvorens de Volkskrant hun sensatie laten spuien.quote:Op woensdag 23 december 2009 14:59 schreef Agno het volgende:
De vraag over wie de 'credit' voor een wetenschappelijke doorbraak krijgt is interessant. Wat telt in de wetenschappelijke wereld: is het altijd degene die als eerste formeel publiceert of is het degene die als eerste publiek gaat? Hoe werkt bijv. zo'n Spinoza lezing? Moeten alle aanwezigen vooraf een soort non-disclosure tekenen?
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Wat natuurlijk ook nog gebeurd kan zijn is dat de desbetreffende journalist (Martijn van Calmthout, die in Utrecht heeft gestudeerd, net als naar ik meende) bij Verlinde zijn lezing is geweest en zelf het artikel heeft geschreven, maar dat kan ik me eigenlijk moeilijk voorstellen.
We hebben in elk geval wat te bespreken tijdens de volgende journalclub
We hebben in elk geval wat te bespreken tijdens de volgende journalclub
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
En er was opeens ook een Wikipedia artikel http://nl.wikipedia.org/wiki/Erik_Verlinde 
Klopt het trouwens wat er staat? Zou het Higgs-deeltje overbodig worden met dat dichtheden verhaal?
(ik wil wel even op de hoogte blijven van dit eigenlijk
toch best fundamenteel onderwerp)
Klopt het trouwens wat er staat? Zou het Higgs-deeltje overbodig worden met dat dichtheden verhaal?
(ik wil wel even op de hoogte blijven van dit eigenlijk
toch best fundamenteel onderwerp)
Nee, waar zie je dat staan? Dit zou een nieuwe kijk op zwaartekracht geven. Het Higgsmechanisme is echter wat anders; dat is een mechanisme om in het standaardmodel deeltjes hun massa te geven en tegelijkertijd ijksymmetrie te behouden.quote:Op maandag 28 december 2009 23:30 schreef Mastertje het volgende:
En er was opeens ook een Wikipedia artikel http://nl.wikipedia.org/wiki/Erik_Verlinde
Klopt het trouwens wat er staat? Zou het Higgs-deeltje overbodig worden met dat dichtheden verhaal
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Dit wordt spannend. Uit de Volkskrant van gisteren.
Fysicus beschuldigt collega van plagiaat
NIEUWE THEORIE De Amsterdamse theoretisch fysicus prof. Erik Verlinde beschuldigt een Indiase fysicus van plagiaat. Thanu Padmanabhan zou enkele formules van Verlinde hebben overgenomen via een weblog en die als eigen werk hebben gepresenteerd op Arxiv.org. Op deze website wil Verlinde zijn nieuwe theorie over de zwaartekracht van Newton publiceren. Daarin leidt hij de gravitatiewet af uit een beschouwing over de manier waarop informatie over een fysisch systeem als een zwart gat verdeeld is over de ruimte eromheen. De Indiër zou zich hebben gebaseerd op een foto van Verlinde in de Volkskrant, waarop de natuurkundige voor een schoolbord staat met daarop enkele van zijn formules.
Fysicus beschuldigt collega van plagiaat
NIEUWE THEORIE De Amsterdamse theoretisch fysicus prof. Erik Verlinde beschuldigt een Indiase fysicus van plagiaat. Thanu Padmanabhan zou enkele formules van Verlinde hebben overgenomen via een weblog en die als eigen werk hebben gepresenteerd op Arxiv.org. Op deze website wil Verlinde zijn nieuwe theorie over de zwaartekracht van Newton publiceren. Daarin leidt hij de gravitatiewet af uit een beschouwing over de manier waarop informatie over een fysisch systeem als een zwart gat verdeeld is over de ruimte eromheen. De Indiër zou zich hebben gebaseerd op een foto van Verlinde in de Volkskrant, waarop de natuurkundige voor een schoolbord staat met daarop enkele van zijn formules.
Ahh, okee, ik weet nog maar vrij weinig van de moderne quantum mechanicaquote:Op donderdag 31 december 2009 11:20 schreef Haushofer het volgende:
[..]
Nee, waar zie je dat staan? Dit zou een nieuwe kijk op zwaartekracht geven. Het Higgsmechanisme is echter wat anders; dat is een mechanisme om in het standaardmodel deeltjes hun massa te geven en tegelijkertijd ijksymmetrie te behouden.
Ik vond het wat raar staan op die wikipedia pagina. ( Interessant gegeven hierbij is dat tot op heden (2009) noch het Higgs deeltje (dat andere elementaire deeltjes hun massa geeft), noch het graviton (dat de zwaartekracht zou overbrengen) experimenteel zijn aangetoond. )Popcorn iemandquote:Op zondag 3 januari 2010 12:58 schreef Agno het volgende:
Dit wordt spannend. Uit de Volkskrant van gisteren.
Fysicus beschuldigt collega van plagiaat
NIEUWE THEORIE De Amsterdamse theoretisch fysicus prof. Erik Verlinde beschuldigt een Indiase fysicus van plagiaat. Thanu Padmanabhan zou enkele formules van Verlinde hebben overgenomen via een weblog en die als eigen werk hebben gepresenteerd op Arxiv.org. Op deze website wil Verlinde zijn nieuwe theorie over de zwaartekracht van Newton publiceren. Daarin leidt hij de gravitatiewet af uit een beschouwing over de manier waarop informatie over een fysisch systeem als een zwart gat verdeeld is over de ruimte eromheen. De Indiër zou zich hebben gebaseerd op een foto van Verlinde in de Volkskrant, waarop de natuurkundige voor een schoolbord staat met daarop enkele van zijn formules.
Hij heeft ook al een 2e versie gepubliceerd op http://arxiv.org/abs/0912.3165[ Bericht 3% gewijzigd door Mastertje op 03-01-2010 14:39:12 ]
Het lijkt erop of dat Padmanabhan nu ook Einstein's veldvergelijkingen ("relativistic gravity") uit de thermodynamica heeft weten af te leiden. Dat hadden we Verlinde nog niet horen claimen.quote:Op zondag 3 januari 2010 14:32 schreef Mastertje het volgende:
[..]
Popcorn iemand
Daarna lijkt ie het afleiden van Newton's gravitatiewetten een beetje te downplayen. Hij presenteert het als een soort bijprodukt van zijn analyse dat alle macroscopische zwaartekrachtswetten te herleiden zijn tot een quantummechanische oorsprong. Daarmee poogt hij wellicht een mogelijke beschuldinging van plagiaat te omzeilen omdat Einstein's gekromde ruimte-tijd een volledigere beschrijving geeft van zwaartekracht dan Newton's wetten (bijv. voor de beschrijving van zwarte gaten).quote:It is possible to provide a physical interpretation for the field equations of gravity based on a thermodynamical perspective. The virtual degrees of freedom associated with the horizons perceived by the local Rindler observers, play a crucial role in this approach.
In this context, the relation S=E/2T between the entropy (S), active gravitational mass (E) and temperature (T), can be reinterpreted as the law of equipartition E = (1/2) nkT where n=A/L_P^2 is the number (density) of microscopic horizon degrees of freedom.
Dit wordt een hele interessante wetenschappelijke fittie.quote:Conversely, one can use the equipartition argument to provide a thermodynamic interpretation of even non-relativistic gravity. These results emphasize the intrinsic quantum nature of all gravitational phenomena and diminishes the distinction between thermal phenomena associated with local Rindler horizons and the usual thermodynamics of macroscopic bodies in non-inertial frames.
|
|
