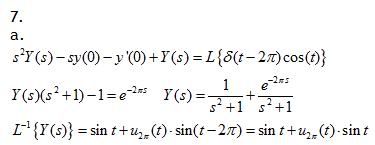SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Kan iemand mij misschien helpen met het berekenen van deze integraal: ∫ sqrt(ex-1) dx (van 0 --> ln2)
Ik heb dit geprobeerd maar is denk ik fout:
∫ sqrt(ex-1) dx | Substitutie met u = ex --> dx = du/ex
∫ sqrt((u -1))/u du
Klopt dit tot nu toe of moet ik het anders aanpakken?
Ik heb nu namelijk geeeeen idee wat ik verder moet doen
Ik heb dit geprobeerd maar is denk ik fout:
∫ sqrt(ex-1) dx | Substitutie met u = ex --> dx = du/ex
∫ sqrt((u -1))/u du
Klopt dit tot nu toe of moet ik het anders aanpakken?
Ik heb nu namelijk geeeeen idee wat ik verder moet doen


Probeer eens u = v2 + 1 te substitueren (dan gaat in elk geval de wortel weg).quote:Op donderdag 3 december 2009 16:35 schreef andrew.16 het volgende:
Kan iemand mij misschien helpen met het berekenen van deze integraal: ∫ sqrt(ex-1) dx (van 0 --> ln2)
Ik heb dit geprobeerd maar is denk ik fout:
∫ sqrt(ex-1) dx | Substitutie met u = ex --> dx = du/ex
∫ sqrt((u -1))/u du
Klopt dit tot nu toe of moet ik het anders aanpakken?
Ik heb nu namelijk geeeeen idee wat ik verder moet doen


Je moet natuurlijk die wortel zien kwijt te raken, en daarvoor moet je een geschiktere substitutie bedenken. Wat we willen is de uitdrukking onder het wortelteken omvormen tot een kwadraat, omdat de wortel uit het kwadraat van een grootheid die grootheid zelf is, of het tegendeel daarvan. Dus willen we een substitutie zodanig dat:quote:Op donderdag 3 december 2009 16:35 schreef andrew.16 het volgende:
Kan iemand mij misschien helpen met het berekenen van deze integraal: ∫ sqrt(ex-1) dx (van 0 --> ln2)
Ik heb dit geprobeerd maar is denk ik fout:
∫ sqrt(ex-1) dx | Substitutie met u = ex --> dx = du/ex
∫ sqrt((u -1))/u du
Klopt dit tot nu toe of moet ik het anders aanpakken?
Ik heb nu namelijk geeeeen idee wat ik verder moet doen
(1) u2 = ex - 1
Oplossen voor x geeft dan:
(2) x = ln(u2 + 1)
En dus hebben we ook:
(3) dx/du = 2u/(u2 + 1)
En dus:
(4) dx = 2u/(u2 + 1)∙du
We hebben nu:
(5) ∫ √(ex - 1)∙dx = ∫ 2u2/(u2 + 1)∙du
Nu heb je ook
(6) 2u2/(u2 + 1) = (2(u2 + 1) - 2)/(u2 + 1) = 2 - 2/(u2 + 1)
En dus:
(7) ∫ 2u2/(u2 + 1)∙du = ∫ (2 - 2/(u2 + 1))∙du = 2u - 2∙arctan u + C
Uit (5) en (7) volgt dan na terugsubstitueren van u = √(ex - 1) dat:
(8) ∫ √(ex - 1)∙dx = 2∙√(ex - 1) - 2∙arctan(√(ex - 1)) + C
Voor de waarde van de bepaalde integraal over het interval [0, ln 2] vinden we dan 2∙(1 - arctan 1) = 2∙(1 - π/4) = 2 - π/2.
[ Bericht 0% gewijzigd door Riparius op 03-12-2009 21:31:01 ]


Bedankt! Was er nooit zelf op gekomen om u2 te doen.quote:Op donderdag 3 december 2009 21:19 schreef Riparius het volgende:
-Knip-


Je kunt ook opmerken: √2·√2 = 2, dus 2/√2 = √2, m.a.w. er staat dus gewoon (√2√3)3 = (√6)3 = 6√6.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


zit een typo in inderdaad; ik gebruik dat √(6/4) = √6 / √4 = √6 / 2.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


quote:Op donderdag 3 december 2009 16:35 schreef andrew.16 het volgende:
Kan iemand mij misschien helpen met het berekenen van deze integraal: ∫ sqrt(ex-1) dx (van 0 --> ln2)
Ik heb dit geprobeerd maar is denk ik fout:
∫ sqrt(ex-1) dx | Substitutie met u = ex --> dx = du/ex
∫ sqrt((u -1))/u du
Klopt dit tot nu toe of moet ik het anders aanpakken?
Ik heb nu namelijk geeeeen idee wat ik verder moet doen
Als je echt je antwoord wil controleren, probeer dan je antwoorden te checken op Wolframalpha.
Het is af en toe at kutten om de juiste input te vinden, maar er staan genoeg examples op de site hoe de invoer werkt.
In jouw geval is het:
http://www.wolframalpha.c(...)m+x%3D0+to+LN%282%29
Kom ook eens spammen in mijn fotoboek :') **En ja, ik zie er goed uit dat hoef je niet nog eens te vermelden! ** ( hihi )


quote:Op zaterdag 5 december 2009 21:30 schreef Illuminator het volgende:
Met behulp van jullie antwoorden en wat gepuzzel van mijn kant ben ik tot het volgende resultaat gekomen. Volgens mij klopt dit en is het ook de beoogde rekenwijze van het boek.
[ afbeelding ]
Opmerkingen?
---
@GlowMouse: de eerste helft van je uitleg snap ik, maar vanaf het onderstaande stuk volg ik het niet meer:
[ afbeelding ]
Hoe kom je van het linker resultaat bij het rechter resultaat? En waarom gebruik je 6/4 in plaats van 3/2? Het antwoord lijkt ook niet helemaal te kloppen, maar misschien zie ik iets over het hoofd.
@Iblis: die methode maakt de som drastisch eenvoudiger. Erg leuk. Jammer genoeg niet altijd toepasbaar bij soortgelijke sommen.
---
In ieder geval erg bedankt voor de uitleg..
En voor jou geldt:
http://www.wolframalpha.c(...)8sqrt%282%29^3%29%29
Heb het topic niet gelezen, maar dus ik weet niet of hier scholieren of studenten zitten,
Ik wil het volgende alleen even meegeven: Een echte beta is lui, en laat de som voor zich uitrekenen en hoeft slechts te weten hoe, en hoe die het toe moet passen
Kom ook eens spammen in mijn fotoboek :') **En ja, ik zie er goed uit dat hoef je niet nog eens te vermelden! ** ( hihi )


Ik zou het niet echt een methode willen noemen, het is gewoon opmerken dat als de teller x bevat en de noemer √x dat je dan in feite gewoon √x in de teller hebt staan. Dat zie je inderdaad niet altijd, maar vaak wel.quote:Op zaterdag 5 december 2009 21:30 schreef Illuminator het volgende:
@Iblis: die methode maakt de som drastisch eenvoudiger. Erg leuk. Jammer genoeg niet altijd toepasbaar bij soortgelijke sommen.
De iets algemenere methode is teller en noemer met de wortel in de noemer vermenigvuldigen. Ik zou b.v. niet eerst die derde macht nemen, maar dan dit doen:
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Van die editor word ik niet veel wijzer, dan maar even zo.
(20-0,64√L)200/√L wordt 4000/√L – 128
Hoe? ik kom er niet uit.
edit: opgelost (20-0,64√L) eerst maal 200 en dan delen door wortel L. Bleef maar puzzelen maar iemand heeft me geholpen. .
.
[ Bericht 41% gewijzigd door borisz op 06-12-2009 17:32:37 ]
(20-0,64√L)200/√L wordt 4000/√L – 128
Hoe? ik kom er niet uit.
edit: opgelost (20-0,64√L) eerst maal 200 en dan delen door wortel L. Bleef maar puzzelen maar iemand heeft me geholpen.
[ Bericht 41% gewijzigd door borisz op 06-12-2009 17:32:37 ]
winnaar wielerprono 2007 :) Last.FM


Heren , waarom wordt die cost niet meegenomen in de Laplace transformatie (die cost, waar die dirac functie in het begin mee wordt vermenigvuldigd). Dank u wel.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Utgaande van bijv. een null hypothesis waar bij
h0: B1+b2=1
h1: b1+b2 niet gelijk aan 1
Met een hoge waarde op een F-test en een lage P waarde (onder 5%) is het toch rejecten van h0 en acceptatie van h1?
h0: B1+b2=1
h1: b1+b2 niet gelijk aan 1
Met een hoge waarde op een F-test en een lage P waarde (onder 5%) is het toch rejecten van h0 en acceptatie van h1?
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.


je hypothesen sluiten elkaar niet uit?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Oeps, sorry. Ik bedoelde niet kleiner dan 1 maar gelijk aan 1.quote:Op maandag 7 december 2009 00:58 schreef GlowMouse het volgende:
je hypothesen sluiten elkaar niet uit?
Utgaande van bijv. een null hypothesis waar bij
h0: B1+b2=1
h1: b1+b2 niet gelijk aan 1
Met een hoge waarde op een F-test en een lage P waarde (onder 5%) is het toch rejecten van h0 en acceptatie van h1?
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.


Bij een lage p-waarde verwerp je de nulhypothese ja. De F-test komt van een regressiemodel? Dan krijg je bij een hoge F-waarde een lage p-waarde.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Bij gelijkblijvende vrijheidsgraden is er gewoon een vaste relatie tussen de P-waarde en de waarde die uit de F-toets naar voren komt. Het maakt dus niet uit of je op basis van een kritische waarde van de F-toets de nulhypothese verwerpt of op basis van de P-waarde. Enige verschil is dat de P-waarde een gemakkelijker inzicht geeft in de significantie van de verwerping van de nulhypohese (bij een kritische P-waarde van 0,05 en een gevonden P-waarde van 0,0499 is de verwerping minder krachtig dan bij een gevonden P-waarde 0,0001).quote:Op maandag 7 december 2009 01:01 schreef sitting_elfling het volgende:
Met een hoge waarde op een F-test en een lage P waarde (onder 5%) is het toch rejecten van h0 en acceptatie van h1?
[ Bericht 4% gewijzigd door Bolkesteijn op 07-12-2009 01:21:44 ]


Ik hoop toch dat je het significantieniveau vantevoren kiest; de p-waarde zegt helemaal niks over de significantie van de verwerping, alleen over de kans op een type-2 fout.quote:Op maandag 7 december 2009 01:16 schreef Bolkesteijn het volgende:
[..]
Enige verschil is dat de P-waarde een gemakkelijker inzicht geeft in de significantie van de verwerping van de nulhypohese.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hij komt inderdaad van een regressie model. Je doet de calculaties, krijgt een hoge F waarde, alleen moet je de mate van kans significantie zelf kiezen. En dan is er de vraag of je de null hypothese verwerpt of niet. Maar sinds P miniem laag is, wordt hij dus verworpen.quote:Op maandag 7 december 2009 01:03 schreef GlowMouse het volgende:
Bij een lage p-waarde verwerp je de nulhypothese ja. De F-test komt van een regressiemodel? Dan krijg je bij een hoge F-waarde een lage p-waarde.
Bedankt!
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.


Maar het is toch zo uitgaande van een regressie model dat bij hoge F er dus een kleine P is, en als die kleine P < 0.05 is h0 wordt verworpen, en vice versa. Dus bij lage F sowieso een hoge p zit?quote:Op maandag 7 december 2009 01:16 schreef Bolkesteijn het volgende:
[..]
Bij gelijkblijvende vrijheidsgraden is er gewoon een vaste relatie tussen de P-waarde en de waarde die uit de F-toets naar voren komt. Het maakt dus niet uit of je op basis van een kritische waarde van de F-toets de nulhypothese verwerpt of op basis van de P-waarde. Enige verschil is dat de P-waarde een gemakkelijker inzicht geeft in de significantie van de verwerping van de nulhypohese (bij een kritische P-waarde van 0,05 en een gevonden P-waarde van 0,0499 is de verwerping minder krachtig dan bij een gevonden P-waarde 0,0001).
Ik moet maar eens een ander econometrie boek aanschaffen.
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.


Begin met Bain & Engelhardt, Introduction to Probability and Mathematical Statistics; staat genoeg in over kansrekening en standaard toetstheorie.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Het significantieniveau hangt toch gewoon af van de betrouwbaarheid die je wenselijk acht? Wat heeft de volgorde er mee te maken? Indien je gevonden P-waarde maar minimaal onder de kritische P-waarde zit is er sprake van een minder krachtige verwerping van H0, dan als de gevonden P-waarde vrijwel gelijk is aan nul en dus ruim onder de kritische P-waarde zit. Zo heb ik het tenminste altijd geinterpreteerd, immers dan zou je ook in het geval van een nog lagere kritische P-waarde H0 verwerpen.quote:Op maandag 7 december 2009 01:18 schreef GlowMouse het volgende:
Ik hoop toch dat je het significantieniveau vantevoren kiest; de p-waarde zegt helemaal niks over de significantie van de verwerping, alleen over de kans op een type-2 fout.


juistquote:Op maandag 7 december 2009 01:31 schreef Bolkesteijn het volgende:
[..]
Het significantieniveau hangt toch gewoon af van de betrouwbaarheid die je wenselijk acht?
Je moet niet je significantieniveau kiezen op basis van je data, anders krijg je gekke dingen.quote:Wat heeft de volgorde er mee te maken?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Oh, zo, ja dat snap ik. Dan ga je jezelf 'rijk rekenen'.quote:Op maandag 7 december 2009 01:35 schreef GlowMouse het volgende:
Je moet niet je significantieniveau kiezen op basis van je data, anders krijg je gekke dingen.


Ik ga d'r vanuit dat die prima is, dus zal hem aanschaffen voor mn examens later in Januari.quote:Op maandag 7 december 2009 01:28 schreef GlowMouse het volgende:
Begin met Bain & Engelhardt, Introduction to Probability and Mathematical Statistics; staat genoeg in over kansrekening en standaard toetstheorie.
Wij hebben hier als hoofdboek Essentials of Econometrics van Gujarati en Porter. En dat boek werkt niet motiverend
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.


Oke, dat was echt helemaal fout, na vandaag weer ploeteren kom ik op het volgende uit. Maakt het nu wel sense?quote:Op woensdag 2 december 2009 23:15 schreef GlowMouse het volgende:
Ln Y = Ln α + K^β1 + L^β2
vandaar kom ik al niet op Y = L * K^β1 * L^β2 zoals je op de eerste regel zegt.
Is het stap per stap nu wel goed? Dus de stappen uitleggen van het initiele Cobb Douglas model naar log Y/L = log K/L
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.