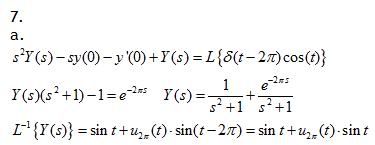[Bèta wiskunde] Huiswerk- en vragentopic

Kan iemand mij misschien helpen met het berekenen van deze integraal: ∫ sqrt(e^x-1) dx (van 0 --> ln2)

Ik heb dit geprobeerd maar is denk ik fout:

∫ sqrt(e^x-1) dx | Substitutie met u = e^x --> dx = du/e^x

∫ sqrt((u -1))/u du


Klopt dit tot nu toe of moet ik het anders aanpakken?
Ik heb nu namelijk geeeeen idee wat ik verder moet doen

quote:

Op donderdag 3 december 2009 16:35 schreef andrew.16 het volgende:
Kan iemand mij misschien helpen met het berekenen van deze integraal: ∫ sqrt(e^x-1) dx (van 0 --> ln2)

Ik heb dit geprobeerd maar is denk ik fout:

∫ sqrt(e^x-1) dx | Substitutie met u = e^x --> dx = du/e^x

∫ sqrt((u -1))/u du


Klopt dit tot nu toe of moet ik het anders aanpakken?
Ik heb nu namelijk geeeeen idee wat ik verder moet doen

Probeer eens u = v² + 1 te substitueren (dan gaat in elk geval de wortel weg).

quote:

Op donderdag 3 december 2009 16:35 schreef andrew.16 het volgende:
Kan iemand mij misschien helpen met het berekenen van deze integraal: ∫ sqrt(e^x-1) dx (van 0 --> ln2)

Ik heb dit geprobeerd maar is denk ik fout:

∫ sqrt(e^x-1) dx | Substitutie met u = e^x --> dx = du/e^x

∫ sqrt((u -1))/u du


Klopt dit tot nu toe of moet ik het anders aanpakken?
Ik heb nu namelijk geeeeen idee wat ik verder moet doen

Je moet natuurlijk die wortel zien kwijt te raken, en daarvoor moet je een geschiktere substitutie bedenken. Wat we willen is de uitdrukking onder het wortelteken omvormen tot een kwadraat, omdat de wortel uit het kwadraat van een grootheid die grootheid zelf is, of het tegendeel daarvan. Dus willen we een substitutie zodanig dat:

(1) u² = e^x - 1

Oplossen voor x geeft dan:

(2) x = ln(u² + 1)

En dus hebben we ook:

(3) dx/du = 2u/(u² + 1)

En dus:

(4) dx = 2u/(u² + 1)∙du

We hebben nu:

(5) ∫ √(e^x - 1)∙dx = ∫ 2u²/(u² + 1)∙du

Nu heb je ook

(6) 2u²/(u² + 1) = (2(u² + 1) - 2)/(u² + 1) = 2 - 2/(u² + 1)

En dus:

(7) ∫ 2u²/(u² + 1)∙du = ∫ (2 - 2/(u² + 1))∙du = 2u - 2∙arctan u + C

Uit (5) en (7) volgt dan na terugsubstitueren van u = √(e^x - 1) dat:

(8) ∫ √(e^x - 1)∙dx = 2∙√(e^x - 1) - 2∙arctan(√(e^x - 1)) + C

Voor de waarde van de bepaalde integraal over het interval [0, ln 2] vinden we dan 2∙(1 - arctan 1) = 2∙(1 - π/4) = 2 - π/2.

[ Bericht 0% gewijzigd door Riparius op 03-12-2009 21:31:01 ]

quote:

Op donderdag 3 december 2009 21:19 schreef Riparius het volgende:
-Knip-

Bedankt! Was er nooit zelf op gekomen om u² te doen.

Je kunt ook opmerken: √2·√2 = 2, dus 2/√2 = √2, m.a.w. er staat dus gewoon (√2√3)³ = (√6)³ = 6√6.

zit een typo in inderdaad; ik gebruik dat √(6/4) = √6 / √4 = √6 / 2.

quote:

Op donderdag 3 december 2009 16:35 schreef andrew.16 het volgende:
Kan iemand mij misschien helpen met het berekenen van deze integraal: ∫ sqrt(e^x-1) dx (van 0 --> ln2)

Ik heb dit geprobeerd maar is denk ik fout:

∫ sqrt(e^x-1) dx | Substitutie met u = e^x --> dx = du/e^x

∫ sqrt((u -1))/u du


Klopt dit tot nu toe of moet ik het anders aanpakken?
Ik heb nu namelijk geeeeen idee wat ik verder moet doen

Als je echt je antwoord wil controleren, probeer dan je antwoorden te checken op Wolframalpha.

Het is af en toe at kutten om de juiste input te vinden, maar er staan genoeg examples op de site hoe de invoer werkt.
In jouw geval is het:

http://www.wolframalpha.c(...)m+x%3D0+to+LN%282%29

quote:

Op zaterdag 5 december 2009 21:30 schreef Illuminator het volgende:
Met behulp van jullie antwoorden en wat gepuzzel van mijn kant ben ik tot het volgende resultaat gekomen. Volgens mij klopt dit en is het ook de beoogde rekenwijze van het boek.

[ afbeelding ]

Opmerkingen?

---

@GlowMouse: de eerste helft van je uitleg snap ik, maar vanaf het onderstaande stuk volg ik het niet meer:

[ afbeelding ]

Hoe kom je van het linker resultaat bij het rechter resultaat? En waarom gebruik je 6/4 in plaats van 3/2? Het antwoord lijkt ook niet helemaal te kloppen, maar misschien zie ik iets over het hoofd.

@Iblis: die methode maakt de som drastisch eenvoudiger. Erg leuk. Jammer genoeg niet altijd toepasbaar bij soortgelijke sommen.

---

In ieder geval erg bedankt voor de uitleg. .

En voor jou geldt:


http://www.wolframalpha.c(...)8sqrt%282%29^3%29%29


Heb het topic niet gelezen, maar dus ik weet niet of hier scholieren of studenten zitten,


Ik wil het volgende alleen even meegeven: Een echte beta is lui, en laat de som voor zich uitrekenen en hoeft slechts te weten hoe, en hoe die het toe moet passen

quote:

Op zaterdag 5 december 2009 21:30 schreef Illuminator het volgende:
@Iblis: die methode maakt de som drastisch eenvoudiger. Erg leuk. Jammer genoeg niet altijd toepasbaar bij soortgelijke sommen.

Ik zou het niet echt een methode willen noemen, het is gewoon opmerken dat als de teller x bevat en de noemer √x dat je dan in feite gewoon √x in de teller hebt staan. Dat zie je inderdaad niet altijd, maar vaak wel.

De iets algemenere methode is teller en noemer met de wortel in de noemer vermenigvuldigen. Ik zou b.v. niet eerst die derde macht nemen, maar dan dit doen:

Van die editor word ik niet veel wijzer, dan maar even zo.

(20-0,64√L)200/√L wordt 4000/√L – 128

Hoe? ik kom er niet uit.

edit: opgelost (20-0,64√L) eerst maal 200 en dan delen door wortel L. Bleef maar puzzelen maar iemand heeft me geholpen. .

[ Bericht 41% gewijzigd door borisz op 06-12-2009 17:32:37 ]

Heren , waarom wordt die cost niet meegenomen in de Laplace transformatie (die cost, waar die dirac functie in het begin mee wordt vermenigvuldigd). Dank u wel.

Utgaande van bijv. een null hypothesis waar bij
h0: B1+b2=1
h1: b1+b2 niet gelijk aan 1

Met een hoge waarde op een F-test en een lage P waarde (onder 5%) is het toch rejecten van h0 en acceptatie van h1?

je hypothesen sluiten elkaar niet uit?

quote:

Op maandag 7 december 2009 00:58 schreef GlowMouse het volgende:
je hypothesen sluiten elkaar niet uit?

Oeps, sorry. Ik bedoelde niet kleiner dan 1 maar gelijk aan 1.

Utgaande van bijv. een null hypothesis waar bij
h0: B1+b2=1
h1: b1+b2 niet gelijk aan 1

Met een hoge waarde op een F-test en een lage P waarde (onder 5%) is het toch rejecten van h0 en acceptatie van h1?

Bij een lage p-waarde verwerp je de nulhypothese ja. De F-test komt van een regressiemodel? Dan krijg je bij een hoge F-waarde een lage p-waarde.

quote:

Op maandag 7 december 2009 01:01 schreef sitting_elfling het volgende:
Met een hoge waarde op een F-test en een lage P waarde (onder 5%) is het toch rejecten van h0 en acceptatie van h1?

Bij gelijkblijvende vrijheidsgraden is er gewoon een vaste relatie tussen de P-waarde en de waarde die uit de F-toets naar voren komt. Het maakt dus niet uit of je op basis van een kritische waarde van de F-toets de nulhypothese verwerpt of op basis van de P-waarde. Enige verschil is dat de P-waarde een gemakkelijker inzicht geeft in de significantie van de verwerping van de nulhypohese (bij een kritische P-waarde van 0,05 en een gevonden P-waarde van 0,0499 is de verwerping minder krachtig dan bij een gevonden P-waarde 0,0001).

[ Bericht 4% gewijzigd door Bolkesteijn op 07-12-2009 01:21:44 ]

quote:

Op maandag 7 december 2009 01:16 schreef Bolkesteijn het volgende:

[..]

Enige verschil is dat de P-waarde een gemakkelijker inzicht geeft in de significantie van de verwerping van de nulhypohese.

Ik hoop toch dat je het significantieniveau vantevoren kiest; de p-waarde zegt helemaal niks over de significantie van de verwerping, alleen over de kans op een type-2 fout.

quote:

Op maandag 7 december 2009 01:03 schreef GlowMouse het volgende:
Bij een lage p-waarde verwerp je de nulhypothese ja. De F-test komt van een regressiemodel? Dan krijg je bij een hoge F-waarde een lage p-waarde.

Hij komt inderdaad van een regressie model. Je doet de calculaties, krijgt een hoge F waarde, alleen moet je de mate van kans significantie zelf kiezen. En dan is er de vraag of je de null hypothese verwerpt of niet. Maar sinds P miniem laag is, wordt hij dus verworpen.

Bedankt!

quote:

Op maandag 7 december 2009 01:16 schreef Bolkesteijn het volgende:

[..]

Bij gelijkblijvende vrijheidsgraden is er gewoon een vaste relatie tussen de P-waarde en de waarde die uit de F-toets naar voren komt. Het maakt dus niet uit of je op basis van een kritische waarde van de F-toets de nulhypothese verwerpt of op basis van de P-waarde. Enige verschil is dat de P-waarde een gemakkelijker inzicht geeft in de significantie van de verwerping van de nulhypohese (bij een kritische P-waarde van 0,05 en een gevonden P-waarde van 0,0499 is de verwerping minder krachtig dan bij een gevonden P-waarde 0,0001).

Maar het is toch zo uitgaande van een regressie model dat bij hoge F er dus een kleine P is, en als die kleine P < 0.05 is h0 wordt verworpen, en vice versa. Dus bij lage F sowieso een hoge p zit?

Ik moet maar eens een ander econometrie boek aanschaffen.

Begin met Bain & Engelhardt, Introduction to Probability and Mathematical Statistics; staat genoeg in over kansrekening en standaard toetstheorie.

quote:

Op maandag 7 december 2009 01:18 schreef GlowMouse het volgende:
Ik hoop toch dat je het significantieniveau vantevoren kiest; de p-waarde zegt helemaal niks over de significantie van de verwerping, alleen over de kans op een type-2 fout.

Het significantieniveau hangt toch gewoon af van de betrouwbaarheid die je wenselijk acht? Wat heeft de volgorde er mee te maken? Indien je gevonden P-waarde maar minimaal onder de kritische P-waarde zit is er sprake van een minder krachtige verwerping van H0, dan als de gevonden P-waarde vrijwel gelijk is aan nul en dus ruim onder de kritische P-waarde zit. Zo heb ik het tenminste altijd geinterpreteerd, immers dan zou je ook in het geval van een nog lagere kritische P-waarde H0 verwerpen.

quote:

Op maandag 7 december 2009 01:31 schreef Bolkesteijn het volgende:

[..]

Het significantieniveau hangt toch gewoon af van de betrouwbaarheid die je wenselijk acht?

juist

quote:

Wat heeft de volgorde er mee te maken?

Je moet niet je significantieniveau kiezen op basis van je data, anders krijg je gekke dingen.

quote:

Op maandag 7 december 2009 01:35 schreef GlowMouse het volgende:
Je moet niet je significantieniveau kiezen op basis van je data, anders krijg je gekke dingen.

Oh, zo, ja dat snap ik. Dan ga je jezelf 'rijk rekenen'.

quote:

Op maandag 7 december 2009 01:28 schreef GlowMouse het volgende:
Begin met Bain & Engelhardt, Introduction to Probability and Mathematical Statistics; staat genoeg in over kansrekening en standaard toetstheorie.

Ik ga d'r vanuit dat die prima is, dus zal hem aanschaffen voor mn examens later in Januari.

Wij hebben hier als hoofdboek Essentials of Econometrics van Gujarati en Porter. En dat boek werkt niet motiverend

quote:

Op woensdag 2 december 2009 23:15 schreef GlowMouse het volgende:
Ln Y = Ln α + K^β1 + L^β2
vandaar kom ik al niet op Y = L * K^β1 * L^β2 zoals je op de eerste regel zegt.

Oke, dat was echt helemaal fout, na vandaag weer ploeteren kom ik op het volgende uit. Maakt het nu wel sense?

Is het stap per stap nu wel goed? Dus de stappen uitleggen van het initiele Cobb Douglas model naar log Y/L = log K/L

Bij kansrekening een tijd gediscussieerd over het volgende vraagstuk. Hoe stom ook, maar wij kwamen er niet uit. Kan iemand mij een beetje de goede kant opsturen? Alvast bedankt.

Voor een bepaalde plaats en tijd doen 2 weerstations, I en II, een weersvoorspelling: regen of zon.
Bekend is dat I in 9 van de 10 gevallen goed voorspelt, en II in 4 van de 5 gevallen.

Vraag: Als I regen voorspelt en II zon, wat is dan de kans op regen?

quote:

Op maandag 7 december 2009 18:52 schreef Hap_Slik het volgende:
Bij kansrekening een tijd gediscussieerd over het volgende vraagstuk. Hoe stom ook, maar wij kwamen er niet uit. Kan iemand mij een beetje de goede kant opsturen? Alvast bedankt.

Voor een bepaalde plaats en tijd doen 2 weerstations, I en II, een weersvoorspelling: regen of zon.
Bekend is dat I in 9 van de 10 gevallen goed voorspelt, en II in 4 van de 5 gevallen.

Vraag: Als I regen voorspelt en II zon, wat is dan de kans op regen?

kun je niet zeggen

quote:

Op maandag 7 december 2009 18:20 schreef sitting_elfling het volgende:

[..]

Oke, dat was echt helemaal fout, na vandaag weer ploeteren kom ik op het volgende uit. Maakt het nu wel sense?

Is het stap per stap nu wel goed? Dus de stappen uitleggen van het initiele Cobb Douglas model naar log Y/L = log K/L

[ afbeelding ]

De rol van u_i in regel 1 is twijfelachtig, verder ziet het er goed uit.

quote:

Op maandag 7 december 2009 18:53 schreef GlowMouse het volgende:

[..]

kun je niet zeggen

Waarom niet dan?

quote:

Op maandag 7 december 2009 18:57 schreef Hap_Slik het volgende:

[..]

Waarom niet dan?

omdat afhankelijkheid een grote rol speelt.

quote:

Op maandag 7 december 2009 18:58 schreef GlowMouse het volgende:

[..]

omdat afhankelijkheid een grote rol speelt.

Zal je dat nader kunnen toelichten, denk dat ik het niet helemaal volg

quote:

Op maandag 7 december 2009 19:05 schreef Hap_Slik het volgende:

[..]

Zal je dat nader kunnen toelichten, denk dat ik het niet helemaal volg

Als die twee weerstations in dezelfde plek staan (wat ze doen) dan hebben ze hetzelfde weer. Het is waarschijnlijk dat alleen in twijfelgevallen een fout gemaakt wordt. Station II doet het vaker fout dan Station I, dus het zou best kunnen dat als Station I het fout heeft, II het ook zeker fout heeft, en II ook soms anders afwijkt.

Met die logica is station I dus ‘leidinggevend’ en zou je die gewoon altijd moeten volgen en is het 9/10 keer correct.

Maar dat is waarschijnlijk niet wat ze bedoelen, ze bedoelen waarschijnlijk dat er helemaal geen verband zit tussen de momenten waarop ze het fout doen. Dat ze het onafhankelijk van elkaar fout doen. Maar je moet je ernstig afvragen of dat wel een realistische situatie is.

quote:

Op maandag 7 december 2009 19:18 schreef Iblis het volgende:

[..]

Als die twee weerstations in dezelfde plek staan (wat ze doen) dan hebben ze hetzelfde weer. Het is waarschijnlijk dat alleen in twijfelgevallen een fout gemaakt wordt. Station II doet het vaker fout dan Station I, dus het zou best kunnen dat als Station I het fout heeft, II het ook zeker fout heeft, en II ook soms anders afwijkt.

Met die logica is station I dus ‘leidinggevend’ en zou je die gewoon altijd moeten volgen en is het 9/10 keer correct.

Maar dat is waarschijnlijk niet wat ze bedoelen, ze bedoelen waarschijnlijk dat er helemaal geen verband zit tussen de momenten waarop ze het fout doen. Dat ze het onafhankelijk van elkaar fout doen. Maar je moet je ernstig afvragen of dat wel een realistische situatie is.

Wat ' ze' bedoelen was nou net de vraag. Oorspronkelijk was het een hoogleraar wiskunde die ermee kwam en toen is een professor kansrekening een beetje uit zijn slof geschoten. De vraag was waarom. En dit is het antwoord dus. Bedankt!

quote:

Op maandag 7 december 2009 19:29 schreef Hap_Slik het volgende:

[..]

Wat ' ze' bedoelen was nou net de vraag. Oorspronkelijk was het een hoogleraar wiskunde die ermee kwam en toen is een professor kansrekening een beetje uit zijn slof geschoten. De vraag was waarom. En dit is het antwoord dus. Bedankt!

Tja, met de extra aanname van onafhankelijkheid is de som wel op te lossen op zich. Maar dan moet je dat even melden. Zo gegeven is er geen oplossing om bovenstaande dus.

quote:

Op maandag 7 december 2009 19:32 schreef Iblis het volgende:

[..]

Tja, met de extra aanname van onafhankelijkheid is de som wel op te lossen op zich. Maar dan moet je dat even melden. Zo gegeven is er geen oplossing om bovenstaande dus.

Nee het ging puur om dit vraagstuk(letterlijk). Want als ze wel onderling afhankelijk zijn met elkaar, wat zal het dan worden ?

quote:

Op maandag 7 december 2009 19:40 schreef Hap_Slik het volgende:

[..]

Nee het ging puur om dit vraagstuk(letterlijk). Want als ze wel onderling afhankelijk zijn met elkaar, wat zal het dan worden ?

Er kan echt vanalles uitkomen, je hebt de simultane kansverdeling nodig. En dat wist die professor ook best.

quote:

Op zondag 6 december 2009 23:40 schreef Burakius het volgende:
[ afbeelding ]

Heren , waarom wordt die cost niet meegenomen in de Laplace transformatie (die cost, waar die dirac functie in het begin mee wordt vermenigvuldigd). Dank u wel.

Niemand hier nog een antwoord op?

cos(2 pi) = 1.

Hoe zou je bovenstaande kunnen vereenvoudigen tot een enkele formule? Als ik het plot is het bijna een e-macht, afgezien dat de uitkomst bij I > 16 natuurlijk 0 is. Oftewel: is afkappen wiskundig te benaderen?

Ik besef me net dat ik eigenlijk geen fuck snap van de letter 'd' in de differentiaalrekening. Het is echt een chinees voor mij die notaties. Heeft iemand toevallig een duidelijke uitleg wat die letter nou in alle gevallen betekent? De andere notaties van functies en afgeleiden etc. snap ik eigenlijk ook niet goed.

Wat ik nu weet:
d betekent soms dat het gaat om een oneindig klein interval. Dus als je dan dy/dx hebt, geeft je daarmee de exacte richtingscoefficient op een bepaalde plek aan, of de functie van alle richtingscoefficienten -> de afgeleide.
Volgens mijn boek is dit dan weer uit te leggen doordat je dx als een 'independent variable' neemt en dy als een 'dependent variable' afhankelijk van dx als volgt: dy = dy/dx * dx = f'(x) * dx
Wat ik nou niet begrijp is waar die dy nou voor staat. Ik kan me er geen beeld bij vormen, algebraisch is het wel logisch, maar wat is nou het nu van het aangeven een 'dy' dan uberhaupt?
En dan beginnen ze vervolgens ook nog die d voor allemaal verschillende soorten elementen te zetten.
Bijv. U = lnx , dU = dx/x
Dat klopt algebraisch, maar wat is die dU dan uberhaupt? De afgeleide van U? Dat kan weer niet want dat is dU/dx al right? De richtingscoefficient van U bij x misschien? En wat is het verschil dan tussen U en U(x)?


Ik ben echt totaal het overzicht kwijt

Veel van die trucs van dy/dx zijn algebraïsch van aard inderdaad en volgen uit Leibniz’ dy/dx notatie. Die ‘werken’, maar er is soms moeilijk een interpretatie aan te geven, daarom houdt ook niet iedereen ervan.

Het is m.i een beetje een notatietruc (maar wel een handige). In principe kan het ook zonder, maar dat is vaak wel omslachtiger noteren.

quote:

Op dinsdag 8 december 2009 14:49 schreef MichielPH het volgende:

[ code verwijderd ]

Hoe zou je bovenstaande kunnen vereenvoudigen tot een enkele formule? Als ik het plot is het bijna een e-macht, afgezien dat de uitkomst bij I > 16 natuurlijk 0 is. Oftewel: is afkappen wiskundig te benaderen?

Een e-macht? Ik snap hem niet volgens mij.

quote:

Op dinsdag 8 december 2009 17:19 schreef Iblis het volgende:
Veel van die trucs van dy/dx zijn algebraïsch van aard inderdaad en volgen uit Leibniz’ dy/dx notatie. Die ‘werken’, maar er is soms moeilijk een interpretatie aan te geven, daarom houdt ook niet iedereen ervan.

Het is m.i een beetje een notatietruc (maar wel een handige). In principe kan het ook zonder, maar dat is vaak wel omslachtiger noteren.

Hmm das lekker Vooral aangezien we er ook mee moeten rekenen bljikbaar.

Wat ik dan nog steeds niet begrijp is het verschil tussen bijvoorbeeld een functie U, U(x), U' en U'(x).
Destemeer omdat je bijv. bij partiële zon vage notatie hebt.
Formule voor partiële integratie:
- Integraal (UdV) = UV - Integraal (dUV)
De notatie voor de afgeleide van U is dU/dx right?
Dus dU is niet gelijk aan U' maar aan U'dx, maar als je de formule gebruikt doe je wel gewoon
integraal(f(x)g'(x)) = f(x)g(x) - integraal (f'(x)g(x)) in plaats van
integraal( f(x) (g'(X)/dx) ) = f(x)g(x) - integraal( ((f'(x)/dx) g(x) )

quote:

Op dinsdag 8 december 2009 17:23 schreef Iblis het volgende:

[..]

Een e-macht? Ik snap hem niet volgens mij.

Stom van me, het grondtal is natuurlijk gewoon 2:

Eerste vergelijking:

Dit valt namelijk te herschrijven tot

Tweede vergelijing:


Ik ben aan de tweede vergelijking gekomen door de eerste vergelijkingen domweg in te vullen en met de getallen de tweede vergelijking te bedenken. Nu is de vraag: Is de tweede vergelijking ook te herleiden zonder getallen in te hoeven vullen?

quote:

Op dinsdag 8 december 2009 16:28 schreef synthesix het volgende:
Ik besef me net dat ik eigenlijk geen fuck snap van de letter 'd' in de differentiaalrekening. Het is echt een chinees voor mij die notaties. Heeft iemand toevallig een duidelijke uitleg wat die letter nou in alle gevallen betekent? De andere notaties van functies en afgeleiden etc. snap ik eigenlijk ook niet goed.

Het is een traditionele notatie die teruggaat op Leibniz en dateert uit de tijd dat men nog geen streng limietbegrip had. Omdat men met dx, dy, althans oorspronkelijk, 'oneindig kleine' grootheden bedoelde aan te geven sprak men dan ook van infinitesimaalrekening.

quote:

Wat ik nu weet:
d betekent soms dat het gaat om een oneindig klein interval. Dus als je dan dy/dx hebt, geeft je daarmee de exacte richtingscoefficient op een bepaalde plek aan, of de functie van alle richtingscoefficienten -> de afgeleide.
Volgens mijn boek is dit dan weer uit te leggen doordat je dx als een 'independent variable' neemt en dy als een 'dependent variable' afhankelijk van dx als volgt: dy = dy/dx * dx = f'(x) * dx

Over welk boek heb je het hier?

quote:

Wat ik nou niet begrijp is waar die dy nou voor staat. Ik kan me er geen beeld bij vormen, algebraisch is het wel logisch, maar wat is nou het nu van het aangeven een 'dy' dan uberhaupt?

De notaties van Leibniz zijn om allerlei redenen erg nuttig, denk alleen maar aan de kettingregel of de substitutiemethode in de integraalrekening. De notatie ∫f(x)dx is trouwens ook van Leibniz afkomstig. Hij correspondeerde veel met de broers Jacob en Johann Bernoulli, die zijn notatie overnamen. Johann Bernoulli gaf Leonard Euler les in zijn jonge jaren, zodat Euler de notatie ook overnam. And the rest, as they say, is history ...

In Engeland bleven ze overigens nog een eeuw doorprutsen met de onhandige notatie van Newton, dit als gevolg van de grote controverse rond de ontdekking van de infinitesimaalrekening. Maar het resultaat daarvan was dat de Britse wiskunde enorm achterop raakte.

quote:

En dan beginnen ze vervolgens ook nog die d voor allemaal verschillende soorten elementen te zetten.
Bijv. U = lnx , dU = dx/x
Dat klopt algebraisch, maar wat is die dU dan uberhaupt? De afgeleide van U? Dat kan weer niet want dat is dU/dx al right? De richtingscoefficient van U bij x misschien? En wat is het verschil dan tussen U en U(x)?

Je kunt bij dx en dy het best de overeenkomst met Δx en Δy in gedachten houden. Als x je onafhankelijke variabele is en y de daarvan afhankelijke variabele, dan is Δy dus het increment van de afhankelijke variabele y als gevolg van het increment Δx in de onafhankelijke variabele x. Evenzo voor dy en dx, zij het dat men zich oorspronkelijk voorstelde dat het hier ging om 'oneindig kleine' (infinitesimale) grootheden.

De notatie U(x) geeft alleen expliciet aan dat een variabele U afhangt van (dus een functie is van ) een variabele x. We noemen x dan de onafhankelijke variabele en U de (daarvan) afhankelijke variabele. Niettemin is hier sprake van een conceptuele verwarring tussen de naam van een functie en de naam van de afhankelijke variabele van die functie, dat is immers niet hetzelfde: je kunt een functie f hebben met als functievoorschrift y = f(x). Dan is y de afhankelijke variabele, maar de functie zelf wordt toch echt aangeduid met f, niet met y.

quote:

Ik ben echt totaal het overzicht kwijt

Ga eens even lekker grasduinen in Wikipedia. De raison d'être van de diverse notaties wordt je dan wel duidelijk.

quote:

Op dinsdag 8 december 2009 18:15 schreef Riparius het volgende:

[..]

Het is een traditionele notatie die teruggaat op Leibniz en dateert uit de tijd dat men nog geen streng limietbegrip had. Omdat men met dx, dy, althans oorspronkelijk, 'oneindig kleine' grootheden bedoelde aan te geven sprak men dan ook van infinitesimaalrekening.
[..]

Over welk boek heb je het hier?
[..]

De notaties van Leibniz zijn om allerlei redenen erg nuttig, denk alleen maar aan de kettingregel of de substitutiemethode in de integraalrekening. De notatie ∫f(x)dx is trouwens ook van Leibniz afkomstig. Hij correspondeerde veel met de broers Jacob en Johann Bernoulli, die zijn notatie overnamen. Johann Bernoulli gaf Leonard Euler les in zijn jonge jaren, zodat Euler de notatie ook overnam. And the rest, as they say, is history ...

In Engeland bleven ze overigens nog een eeuw doorprutsen met de onhandige notatie van Newton, dit als gevolg van de grote controverse rond de ontdekking van de infinitesimaalrekening. Maar het resultaat daarvan was dat de Britse wiskunde enorm achterop raakte.
[..]

Je kunt bij dx en dy het best de overeenkomst met Δx en Δy in gedachten houden. Als x je onafhankelijke variabele is en y de daarvan afhankelijke variabele, dan is Δy dus het increment van de afhankelijke variabele y als gevolg van het increment Δx in de onafhankelijke variabele x. Evenzo voor dy en dx, zij het dat men zich oorspronkelijk voorstelde dat het hier ging om 'oneindig kleine' (infinitesimale) grootheden.

De notatie U(x) geeft alleen expliciet aan dat een variabele U afhangt van (dus een functie is van ) een variabele x. We noemen x dan de onafhankelijke variabele en U de (daarvan) afhankelijke variabele. Niettemin is hier sprake van een conceptuele verwarring tussen de naam van een functie en de naam van de afhankelijke variabele van die functie, dat is immers niet hetzelfde: je kunt een functie f hebben met als functievoorschrift y = f(x). Dan is y de afhankelijke variabele, maar de functie zelf wordt toch echt aangeduid met f, niet met y.
[..]

Ga eens even lekker grasduinen in Wikipedia. De raison d'être van de diverse notaties wordt je dan wel duidelijk.

Thanks ^^ het begon al een beetje duidelijker te worden onderhand, ik snap het idee van de notatie nu wel ongeveer. Het gaat trouwens om "Calculus: A complete course van Robert Adams, Christopher Essex (et al. ?)"
(Ik zat ook al te grasduinen in google, blijkt dat ik niet de enige ben met dit probleem trouwens )

Wat ik nog steeds niet echt begrijp is die notatie van functies:
Je geeft met U(x) dus aan dat de waarde van U afhankelijk is van x, maar als je bijvoorbeeld dU/dx noteert, dan is U nog steeds afhankelijk van x. Waarom gebruik je dan gewoon U ipv U(x)?

dU/dx wordt gehanteerd als er geen verwarring is, net als b.v. met f', je ziet soms f'(x), soms f'. Er is (meestal) geen verschil.

ik heb een vraag over een 5 x 5 matrix. (voordat iemand meteen verwijst naar een internetpagina, ze gaan allemaal over een matrix met nullen aan het begin, en die zijn anders).

Ik heb de volgende matrix:

1 2 4 0 1
2 4 0 1 1
4 0 1 1 2
0 1 1 2 4
1 1 2 4 0

Kan iemand mij vertellen hoe ik hier de determined van moet vinden?

Alvast bedankt!!

Kloontje

Wat je je eerst moet beseffen is dat dit een vierkante matrix is, en dat je daarom de determinant kunt bepalen. Er zijn meerdere manieren om de determinant te bepalen, waarvan ik er drie zal uitlichten.

1:Ontwikkelen

Je moet een kolom of rij kiezen die je wilt gebruiken. Kies een rij of een kolom uit waarin de meeste nullen zitten. In dit geval maakt het niet veel uit. Stel we kiezen de eerste rij om de determinant mee te bepalen.

Dit betekent dat we met de 1ste rij gaan "ontwikkelen".

Je pakt de eerste " set " die je gaat uitrekenen: [1 2 , 2 4] (een , betekent dat het eronder ligt, ik ben niet goed met de layout etc.) Je moet je beseffen dat er een schaakbord patroon aanwezig is van + en - . D.w.z. : +1 -2 +4 -0 +1 etc. Het eerste cijfer van je rij is +1. Dus je neemt + 1. Wat je daarna doet is een soort van eigen methode die ik heb bedacht. Je kruist in gedachte de eerste rij weg en de eerste kolom (omdat je dus de 1ste rij hebt gekozen). Wat je overhoudt, daar moet je die + 1 mee vermenigvuldigen. Dus dat wordt:

+1 *
| 4 0 1 1 |
| 0 1 1 2 |
| 1 1 2 4 |
| 1 2 4 0 |
Daarna ga je verder met de volgende cijfer van je rij:

+ (-2) *
| etc. etc. |

Deze methode duurt mij eigenlijk te lang.

Wat je kunt doen is een bovendriehoeksmatrix of een onderdriehoeksmatrix vinden. De diagonaal daarvan (vermenigvuldigd) is ook de determinant.

Mijn rekenmachine geeft als det: 1048 op, maar ik weet niet of ik dit nu goed heb gedaan. Iemand die het wil verifieren.

Je kunt ook met rijoperaties de matrix in driehoeksvorm brengen, als je bijhoudt hoe de determinant dan verandert.