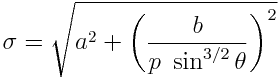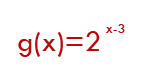SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Modulo 17 bestaat er geen even of oneven, 2 is immers inverteerbaar. Delen door 2 is ofwel 2n=1 mod 17 oplossen (bijvoorbeeld met Euclides als) ofwel direct zien dat 9 een inverse van 2 is en dus met 9 vermenigvuldigen.quote:Op donderdag 22 oktober 2009 21:04 schreef Borizzz het volgende:
Nog eens legendre symbolen
x2 +7x+13 = 0 mod 17 oplossen.
Dit wilde ik doen met kwadraat afsplitsen, dus als k2 = c (mod 17) schrijven.
maar 7 is oneven. Hoe kan ik dit doen? Vermenigvuldigen met inverse van 7 (mod 17)? Of een ander handigheidje?


Oh, zo oké. Dus x1+x2=3 dan.quote:Op donderdag 22 oktober 2009 21:16 schreef GlowMouse het volgende:
[..]
x1 = 1-l
x2 = 2+l
je kunt het omschrijven naar bv. x2 = (1-l)+1+2l = x1+1+2l maar als je l dan invult dan heb je helemaal geen garantie meer dat x1=1-l want voor x1 kun je dan nog alles kiezen.
De juiste methode is om l helemaal kwijt te raken. Dat lukt bv. door beide vergelijkingen op te tellen.


Laatste keer vanavond dat ik stoor:
Klopt het dat wanneer f(x) = 5 . ewortel[6x], dan is f'(x) = 5 . ewortel[6x] . 3x-1/2 ?
Heb dan de kettingregel en de productregel gebruikt.
Klopt het dat wanneer f(x) = 5 . ewortel[6x], dan is f'(x) = 5 . ewortel[6x] . 3x-1/2 ?
Heb dan de kettingregel en de productregel gebruikt.
Oh really?


De afgeleide van wortel[6x] is 3*(6x)^(-0.5)
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Nee, klopt niet.quote:Op donderdag 22 oktober 2009 21:58 schreef Matthijs- het volgende:
Laatste keer vanavond dat ik stoor:
Klopt het dat wanneer f(x) = 5 . ewortel[6x], dan is f'(x) = 5 . ewortel[6x] . 3x-1/2 ?
Heb dan de kettingregel en de productregel gebruikt.


Hoe herschrijf je wortel[6x] dan GM? Ik had het herschreven als 6x-1/2, wat waarschijnlijk de foute differentiatie opleverde.quote:Op donderdag 22 oktober 2009 22:00 schreef GlowMouse het volgende:
De afgeleide van wortel[6x] is 3*(6x)^(-0.5)
Ik en wiskunde
Oh really?


Doe maar (6x)1/2quote:Op donderdag 22 oktober 2009 22:12 schreef Matthijs- het volgende:
[..]
Hoe herschrijf je wortel[6x] dan GM? Ik had het herschreven als 6x-1/2, wat waarschijnlijk de foute differentiatie opleverde.
Ik en wiskunde
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


In het algemeen geldt (ab)^c = a^c * b^c.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dat is het niet.quote:Op donderdag 22 oktober 2009 22:15 schreef Matthijs- het volgende:
[..]
Maar waarom is de afgeleide daarvan dan 18x-1/2?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Rondje spreek je uit als 'na'. S na T Dus eerst T dan S: S(T(x)).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik heb een vraagje over elliptische krommen.
Gegeven een rationaal punt (a,b) op de kromme gedefinieerd door de vergelijking y2=-x4+ c (met c een rationaal getal ongelijk aan 0) wil ik deze vergelijking transformeren tot de weierstrass vgl y'2 =(polynoom van graad 3).
Enig idee hoe dat werkte?
Gegeven een rationaal punt (a,b) op de kromme gedefinieerd door de vergelijking y2=-x4+ c (met c een rationaal getal ongelijk aan 0) wil ik deze vergelijking transformeren tot de weierstrass vgl y'2 =(polynoom van graad 3).
Enig idee hoe dat werkte?


Ken je Riemann-Roch?quote:Op vrijdag 23 oktober 2009 12:41 schreef Optimistic1 het volgende:
Ik heb een vraagje over elliptische krommen.
Gegeven een rationaal punt (a,b) op de kromme gedefinieerd door de vergelijking y2=-x4+ c (met c een rationaal getal ongelijk aan 0) wil ik deze vergelijking transformeren tot de weierstrass vgl y'2 =(polynoom van graad 3).
Enig idee hoe dat werkte?


Calculus 17.1 vraag 21:
y'' + 16y = 0
y(pi/4) = -3
y'(pi/4) = 4
Ik heb bij die opgave moeite met het begrijpen van een tussenstap die ik op een uitwerking vond. (Toen ik het op mezelf probeerde kwam ik niet van de dubbele paren sinus en cosinus af.
Hier is mijn poging:
Als afbeelding:
y'' + 16y = 0
y(pi/4) = -3
y'(pi/4) = 4
Ik heb bij die opgave moeite met het begrijpen van een tussenstap die ik op een uitwerking vond. (Toen ik het op mezelf probeerde kwam ik niet van de dubbele paren sinus en cosinus af.
| 1 2 | y = c_1 cos(4x) + c_2 sin(4x) |
Hier is mijn poging:
| 1 2 3 4 5 | y = c_1 * e ^ 4 (cos x - i sin x) + c_2 * e ^ 4 (cos x - i sin x) \\ y = (c_1 + c_2) * e ^ 4 (cos x - i sin x) \\ how? \\ y = c_1 cos(4x) + c_2 sin(4x) \\ |
Als afbeelding:
Jesus hates you.


Klopt geen hout van, je respecteert om te beginnen de elementaire rekenregels voor machten al niet. Je kunt niet zomaar die e-macht (met een reële exponent) buiten haakjes halen. Oftewel, apq is niet hetzelfde als het product van ap en aq.quote:Op vrijdag 23 oktober 2009 17:17 schreef Hondenbrokken het volgende:
Calculus 17.1 vraag 21:
y'' + 16y = 0
y(pi/4) = -3
y'(pi/4) = 4
Ik heb bij die opgave moeite met het begrijpen van een tussenstap die ik op een uitwerking vond. (Toen ik het op mezelf probeerde kwam ik niet van de dubbele paren sinus en cosinus af.
[ code verwijderd ]
Hier is mijn poging:
[ code verwijderd ]
Als afbeelding:
[ afbeelding ]
[ Bericht 0% gewijzigd door Riparius op 23-10-2009 17:40:51 ]


Je hebt gelijk. Die exponenten worden vermenigvuldigd in plaats van opgeteld.
Dan krijg ik:
En het maakt natuurlijk niet uit hoe je de constanten noemt.
Dan krijg ik:
| 1 2 3 4 5 6 7 | y = c_1 * (cos 4x - i sin 4x) + c_2 * (cos -4x - i sin -4x) \\ y = c_1 * (cos 4x - i sin 4x) + c_2 * (cos 4x + i sin 4x) \\ y = (c_1 + c_2) * (cos 4x) + (c_2 - c_1) * sin(4x) \\ \\ Subs: d_1 = (c_1 + c_2) en d_2 = (c_2 - c_1) \\ y = d_1 * (cos 4x) + d_2 * sin(4x) \\ |
En het maakt natuurlijk niet uit hoe je de constanten noemt.
Jesus hates you.


Dit is nog steeds niet goed. Je kent toch wel de formule van Euler:quote:Op vrijdag 23 oktober 2009 19:37 schreef Hondenbrokken het volgende:
Je hebt gelijk. Die exponenten worden vermenigvuldigd in plaats van opgeteld.
Dan krijg ik:
[ code verwijderd ]
En het maakt natuurlijk niet uit hoe je de constanten noemt.
eiφ = cos φ + i∙sin φ
En waar blijft in jouw uitwerking die i bij je sinustermen?


| 1 2 3 4 5 6 7 | y = c_1 * (\cos 4x + i \sin 4x) + c_2 * (\cos -4x + i \sin -4x) \\ y = c_1 * (\cos 4x + i \sin 4x) + c_2 * (\cos 4x - i \sin 4x) \\ y = (c_1 + c_2) * (\cos 4x) + (c_1 - c_2) * i \sin(4x) \\ \\ Subs: d_1 = (c_1 + c_2) ; d_2 = (c_1 - c_2) \\ y = d_1 * (\cos 4x) + d_2 * i \sin(4x) \\ |
Maar dan snap ik alsnog niet hoe ik van die i af moet komen.
Jesus hates you.


Nou, niet door de i te verdonkeremanen natuurlijk. Je hebt:quote:Op vrijdag 23 oktober 2009 20:27 schreef Hondenbrokken het volgende:
[ code verwijderd ]
Maar dan snap ik alsnog niet hoe ik van die i af moet komen.
d1 = c1 + c2
d2 = i∙(c1 - c2)
Dan zijn de oplossingen van de DV te schrijven als:
y = d1∙cos 4x + d2∙sin 4x
Wat is nu het probleem?


Ik ken de stelling zoals het in Silverman staat. Die stelling 'geeft' geen algortime om gegeven een rationaal punt op 'y^2= (irri. polynoom van graad 4) om dit te transformeren tot een elliptische kromme. In het boek van Cassels is er wel een algortime dat een aantal transformaties gebruikt. Ik geloof dat Riemann-Roch kan helpen uitleggen hoe men op het idee komt dit soort transformaties te doen maar bij mijn ontbreekt het inzicht.quote:


Klopt, er zijn inderdaad een aantal boeken die met formules goochelen. Dat zijn van die methoden die je nooit kunt onthouden. Zou je zoiets willen toepassen, moet je elke keer weer dat boek erbij pakken.quote:Op zaterdag 24 oktober 2009 13:01 schreef Optimistic1 het volgende:
[..]
Ik ken de stelling zoals het in Silverman staat. Die stelling 'geeft' geen algortime om gegeven een rationaal punt op 'y^2= (irri. polynoom van graad 4) om dit te transformeren tot een elliptische kromme. In het boek van Cassels is er wel een algortime dat een aantal transformaties gebruikt. Ik geloof dat Riemann-Roch kan helpen uitleggen hoe men op het idee komt dit soort transformaties te doen maar bij mijn ontbreekt het inzicht.
Met Riemann-Roch heb je een methode die in je hoofd past. Misschien dat die methode wat meer stappen vergt, maar je begrijpt in elk geval wat je aan het doen bent.
Goed, R-R dus. Zij C je kromme en P een rationaal punt op C. We gaan ervan uit dat C compleet en niet-singulier is. Voor gehele n heb je de ruimte L(nP) van rationale functies op C die in P een pool van orde hooguit n hebben en buiten P regulier zijn. De ruimte L(nP) is eindig-dimensionaal en R-R zegt iets over de dimensie ervan. In het geval van krommen van geslacht 1 kun je op die manier zelfs precies de dimensie bepalen. Er komt dan het volgende uit:
dim L(nP) = 0 als n<0 (niet-constante functies hebben evenveel nulpunten als polen, geteld met multipliciteit),
dim L(nP) = 1 als n=0 of n=1 (je hebt dan alleen constante functies),
dim L(nP) = n als n>1 (dus als je n groter maakt krijg je altijd functies die je nog niet eerder had).
Hieruit volgt dat L(2P) een niet-constante functie x bevat en L(3P) een y bevat die niet al in L(2P) ligt.
Nu zitten x3, x2, x, 1, y2, xy, y allemaal in L(6P). Dit zijn 7 elementen van een 6-dimensionale ruimte, dus er is een relatie tussen. Die relatie geeft je een Weierstrassvgl.
Nu geeft het bovenstaande nog niet een manier om de x en de y ook te vinden. Dat gaan we ook pas doen als je eerst goed begrijpt wat ik zojuist ingetikt heb.


Magma kan het. Maar dat is geen gratis programma dus dan moet je maar hopen dat je universiteit het heeft.quote:Op zaterdag 24 oktober 2009 13:31 schreef Optimistic1 het volgende:
Bestaat er een programma dat dat doet? ik zie dat dat algoritme veel prutswerk is.


Ik heb een coole site gevonden. Je kunt er van alles en nog wat berekenen! Ik dacht ik deel het met jullie:
http://www.martindalecenter.com/Calculators.html
http://www.martindalecenter.com/Calculators.html
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Hoi S&S:
Ik heb een vraag over de normaalkromme. Wat ik weet:
De kans om in het rode gebied te vallen is 68%. (1 Sigma buiten het gemiddelde, zo zeg je dat toch?)
De kans om in het groene gebied te vallen is 27% (2 sigma buiten het gemiddelde)
De kans om buiten de groene en rode gebieden te vallen is 5%.
Mijn vraag: Weet iemand wat de exacte kans zijn om in het gebied van 3 sigma, 4 sigma en 5 sigma te vallen. Ik weet dat die kansen zeer klein zijn, maar ik kan ze nergens vinden op internet en ben vergeten of je dat ook zelf kan berekenen.
Ik heb een vraag over de normaalkromme. Wat ik weet:
De kans om in het rode gebied te vallen is 68%. (1 Sigma buiten het gemiddelde, zo zeg je dat toch?)
De kans om in het groene gebied te vallen is 27% (2 sigma buiten het gemiddelde)
De kans om buiten de groene en rode gebieden te vallen is 5%.
Mijn vraag: Weet iemand wat de exacte kans zijn om in het gebied van 3 sigma, 4 sigma en 5 sigma te vallen. Ik weet dat die kansen zeer klein zijn, maar ik kan ze nergens vinden op internet en ben vergeten of je dat ook zelf kan berekenen.
How you play the cards you are dealt is all that matters.


hier heb je het lijstje:
| 1 2 3 4 5 6 7 8 9 10 11 | >> 2*(normcdf( i)-normcdf(i-1)) ans = 0.68268949213709 0.27181024396656 0.04280046783310 0.00263645357959 0.00006276918052 0.00000057132997 |
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dankjewel.quote:Op zaterdag 24 oktober 2009 20:57 schreef GlowMouse het volgende:
hier heb je het lijstje:
[ code verwijderd ]
How you play the cards you are dealt is all that matters.


Kan iemand hier mij grafisch tonen hoe het nou zit met codomein. Gewoon een voorbeeld in een grafiek ofzo, wat nou precies het codomein is. Jipjanneke stijl. Want codomein is ook bereik toch? Echt een epic fail ben ik 
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Kijk even naar het plaatje bij dit artikel. Bereik en codomein zijn niet hetzelfde begrip. Het is wel zo dat het bereik altijd een deelverzameling van het codomein is, dus bereik en codomein kunnen wel samenvallen.quote:Op zaterdag 24 oktober 2009 21:26 schreef Burakius het volgende:
Kan iemand hier mij grafisch tonen hoe het nou zit met codomein. Gewoon een voorbeeld in een grafiek ofzo, wat nou precies het codomein is. Jipjanneke stijl. Want codomein is ook bereik toch? Echt een epic fail ben ik


Ja die had ik al bekeken en snapte er vrij weinig van. Is het niet mogelijk een grafiekje te tekenen ofzo waarin ze staan aangegeven?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Er is verder weinig aan te tekenen. Neem als voorbeeld de functiequote:Op zaterdag 24 oktober 2009 22:16 schreef Burakius het volgende:
Ja die had ik al bekeken en snapte er vrij weinig van. Is het niet mogelijk een grafiekje te tekenen ofzo waarin ze staan aangegeven?
f: ℝ ↦ ℝ,
gedefinieerd door f(x) = x2, of zoals het (in een soort hybride notatie) ook wel wordt geschreven:
f: x ↦ x2
Dan is de verzameling ℝ van de reële getallen het domein van de functie en tevens het codomein, maar het bereik bestaat uit de niet-negatieve reële getallen, want het kwadraat van een reëel getal is immers nooit negatief.


Bij een (formele) definitie van een functie geef je ook het domein en het codomein, b.v.:
f(x): , x ex.
De definitie zegt: het domein (in rood) is ℝ en het codomein (in blauw) is óók ℝ. Dus je kijkt gewoon naar de functiedefinitie om domein en codomein af te lezen.
Het bereik hangt echter (formeel) gezien af van de waarden die daadwerkelijk optreden, in het geval van ex zijn dit alleen positieve getallen, kortom het bereik van die functie is ℝ+. En dat is ook wat dat plaatje laat zien:
Bron: Wikipedia. Maker: Damien Karras. Publiek Domein.
Het domein is rood, het codomein is blauw, en het bereik is gelig. Dit omdat het bereik niet hoeft samen te vallen met het codomein. Soms is dit wel het geval, heb je b.v.:
f(x): ℝ → ℝ, x 2x dan is zowel codomein als bereik ℝ.
f(x): , x ex.
De definitie zegt: het domein (in rood) is ℝ en het codomein (in blauw) is óók ℝ. Dus je kijkt gewoon naar de functiedefinitie om domein en codomein af te lezen.
Het bereik hangt echter (formeel) gezien af van de waarden die daadwerkelijk optreden, in het geval van ex zijn dit alleen positieve getallen, kortom het bereik van die functie is ℝ+. En dat is ook wat dat plaatje laat zien:
Bron: Wikipedia. Maker: Damien Karras. Publiek Domein.
Het domein is rood, het codomein is blauw, en het bereik is gelig. Dit omdat het bereik niet hoeft samen te vallen met het codomein. Soms is dit wel het geval, heb je b.v.:
f(x): ℝ → ℝ, x 2x dan is zowel codomein als bereik ℝ.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Oke dus als ik het goed begrijp, is het "domein" de getallen die je kunt invullen voor een functie waarbij deze geldig is. En de codomein is het resultaat van het invullen van die reële getallen. Zoals bij het voorbeeld is dan bij het invullen van x^2 nooit een negatief getal mogelijk. Waardoor het bereik alle positieve getallen van R is.
Ik snap het begrip bereik dan. Maar het begrip codomein is mij dan nog een beetje vaag. Is er een voorbeeld te geven waarbij domein en codomein verschillend zijn?
Ik snap het begrip bereik dan. Maar het begrip codomein is mij dan nog een beetje vaag. Is er een voorbeeld te geven waarbij domein en codomein verschillend zijn?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Codomein is gewoon een definitiekwestie, als iemand zegt:
f(x): ℝ → , x x2, dan is het codomein dus alle niet-negatieve getallen.
Of neem b.v. | | voor 2-dimensionale vectoren:
|v|: ℝ2 → ℝ, v √(v1˛ + v2˛).
Domein is ℝ˛, codomein ℝ (volgt gewoon uit de definitie), maar het bereik is natuurlijk alleen de positieve getallen, want een vector heeft geen negatieve lengte.
f(x): ℝ → , x x2, dan is het codomein dus alle niet-negatieve getallen.
Of neem b.v. | | voor 2-dimensionale vectoren:
|v|: ℝ2 → ℝ, v √(v1˛ + v2˛).
Domein is ℝ˛, codomein ℝ (volgt gewoon uit de definitie), maar het bereik is natuurlijk alleen de positieve getallen, want een vector heeft geen negatieve lengte.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Oke nou het is me eindelijk duidelijk. Nu ga ik Fermat oplossen (of spel ik die dude zijn achternaam nog steeds verkeerd  )
)
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Ik kan je de Kleine stelling van Fermat dan aanraden om mee te beginnen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Laat ik eerst me pre-master + master halenquote:Op zaterdag 24 oktober 2009 23:07 schreef Iblis het volgende:
Ik kan je de Kleine stelling van Fermat dan aanraden om mee te beginnen.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Zoals ik het begrijp is codomein het domein van de inverse.
Alleen als f(x) = x^2 dan heeft f(x): R -> R geen zin, want de inverse f{^-1}(x) = sqrt(x) geeft als x < 0 complexe resultaten en die vallen buiten R, dus hebben die dan geen oplossing, dus dan kan R helemaal geen codomein van f zijn.
Dus ik snap het eigenlijk nog steeds niet.
Alleen als f(x) = x^2 dan heeft f(x): R -> R geen zin, want de inverse f{^-1}(x) = sqrt(x) geeft als x < 0 complexe resultaten en die vallen buiten R, dus hebben die dan geen oplossing, dus dan kan R helemaal geen codomein van f zijn.
Dus ik snap het eigenlijk nog steeds niet.
Jesus hates you.


Nee, dat is het bereik (mits f inverteerbaar is). Lees de posts hierboven; Riparius legt het prima uit.quote:Op zondag 25 oktober 2009 10:31 schreef Hondenbrokken het volgende:
Zoals ik het begrijp is codomein het domein van de inverse.
Alleen als f(x) = x^2 dan heeft f(x): R -> R geen zin, want de inverse f{^-1}(x) = sqrt(x) geeft als x < 0 complexe resultaten en die vallen buiten R, dus hebben die dan geen oplossing, dus dan kan R helemaal geen codomein van f zijn.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik heb een vraag over een som invoeren in excell.
De som is
Hoe doe ik die met haakjes en dakjes invoeren dat hij niet denkt dat die -3 geen deel meer is van het verband?
De som is
Hoe doe ik die met haakjes en dakjes invoeren dat hij niet denkt dat die -3 geen deel meer is van het verband?


wat bedoel je met 'geen deel van het verband'?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik weet het ook niet helemaal meerquote:Op zondag 25 oktober 2009 @ 13:44 schreef GlowMouse het volgende:
wat bedoel je met 'geen deel van het verband'?
Volgens mij maak ik het alleen maar moeilijker om te begrijpen


Zoals hij daar staat wil je =2^(x-3).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Nog een vraag (Lekker bezig  )
)
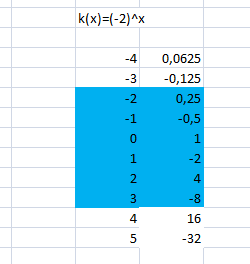
Nu moet ik een exponentiele functie doen.
Die lopen vloeiend enzo.
Hoe kán dit de uitkomst zijn? Ik heb alleen geprobeerd om (-2)^x te doen, en -2^x, maar allebei heeft dezelfde uitkomst. Ik ben niet wiskundig, maar wat er uit deze berekening komt is géén exponentiele functie.
Wat heb ik verkeerd gedaan?
Nu moet ik een exponentiele functie doen.
Die lopen vloeiend enzo.
Hoe kán dit de uitkomst zijn? Ik heb alleen geprobeerd om (-2)^x te doen, en -2^x, maar allebei heeft dezelfde uitkomst. Ik ben niet wiskundig, maar wat er uit deze berekening komt is géén exponentiele functie.
Wat heb ik verkeerd gedaan?


Je hebt nu f(x) = a*b^t met a=1 en b=-2. En dat is geen exponentiële functie want dan moet b positief zijn.
-2^x zou wel een andere grafiek moeten geven (dan a=-1 en b=2).
-2^x zou wel een andere grafiek moeten geven (dan a=-1 en b=2).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


-2^x geeft juist die tabel, even kijken wat er gebeurt met haakjes bij allesquote:Op zondag 25 oktober 2009 @ 14:54 schreef GlowMouse het volgende:
Je hebt nu f(x) = a*b^t met a=1 en b=-2. En dat is geen exponentiële functie want dan moet b positief zijn.
-2^x zou wel een andere grafiek moeten geven (dan a=-1 en b=2).
Edit, met haakjes is het hetzelfde