Ik moet het volgende differentieren: sqrt[4x-x^2].
Je moet met de kettingregel werken, dus dan krijg je
1/(2sqrt[4x-x^2]) * 4 - 2x * -2 leek mij. Uit het antwoord blijkt dat die laatste -2 niet meetelt, waarom niet? Ook op http://www.calc101.com/webMathematica/derivatives.jsp#topdoit doet hij niet mee.
En dan dnek je dat je differentieren na 3 jaar wel kunt... gek word ik er van
[ Bericht 1% gewijzigd door yootje op 14-05-2007 11:47:14 ]
De formule die je hier toe moet passen is volgens mij (a^b)' = b * a * a'
wat jij doet is (a^b)' = b * a * a' * a''
(a = 4x-x^2 en b = 1/2)
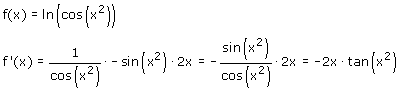
met ketting regel dus 1/(2sqrt[4x-x^2])*[4x-x^2]'
[4x-x^2]' = 4-2x, dus krijg je
1/(2sqrt[4x-x^2])*4-2x
quote:Klopt als een bus op die manier, dacht ik zo.Op maandag 14 mei 2007 12:40 schreef Spaceman89 het volgende:
waarom die -2 erbij? standaardafgeleide van een wortelfunctie is 1/(2sqrt[x])
met ketting regel dus 1/(2sqrt[4x-x^2])*[4x-x^2]'
[4x-x^2]' = 4-2x, dus krijg je
1/(2sqrt[4x-x^2])*4-2x
g(a) = ln(a) dan is g'(a) 1/a * a'
a is dan cos (x^2) en dan gebruik je:
h(b) = cos (b) dan is h'(b) = -sin (b) * b'
waarbij b gelijk is aan x^2
maar in je eerste voorbeeld is het gedeelte waar je nog de afgeleide van wil nemen 4x-x^2 en dat los je zonder kettingregel op.
quote:Bedankt voor je uitleg!Op maandag 14 mei 2007 12:57 schreef Alfje het volgende:
In je 2de voorbeeld pas je de kettingregel2 keer toe omdat je na de eerste keer nog een afgeleide uit moet rekenen waar je ook de kettingregel bij nodig hebt.
g(a) = ln(a) dan is g'(a) 1/a * a'
a is dan cos (x^2) en dan gebruik je:
h(b) = cos (b) dan is h'(b) = -sin (b) * b'
waarbij b gelijk is aan x^2
maar in je eerste voorbeeld is het gedeelte waar je nog de afgeleide van wil nemen 4x-x^2 en dat los je zonder kettingregel op.
quote:wheheh die komt uit 1 van de examens, daar kwam ik ook niet uitOp maandag 14 mei 2007 11:37 schreef yootje het volgende:
Hoi allemaal, ik ben bezig met het examen 2006-I, en er is maar iets waar ik niet uitkom.
Ik moet het volgende differentieren: sqrt[4x-x^2].
Je moet met de kettingregel werken, dus dan krijg je
1/(2sqrt[4x-x^2]) * 4 - 2x * -2 leek mij. Uit het antwoord blijkt dat die laatste -2 niet meetelt, waarom niet? Ook op http://www.calc101.com/webMathematica/derivatives.jsp#topdoit doet hij niet mee.
En dan dnek je dat je differentieren na 3 jaar wel kunt... gek word ik er van
Als je de marginale kosten moet uitrekenen moet je de formule afleiden en dan x invullen?
quote:Die inhoudsvraag erna snapte ik juist wel, alhoewel ik hem wle lastig vond.Op maandag 14 mei 2007 16:21 schreef Game_Error het volgende:
[..]
wheheh die komt uit 1 van de examens, daar kwam ik ook niet uitof wacht, dat was primitiveren
quote:squirten?
quote:Wij hadden die opgave in een schoolexamenOp maandag 14 mei 2007 11:37 schreef yootje het volgende:
Hoi allemaal, ik ben bezig met het examen 2006-I, en er is maar iets waar ik niet uitkom.
Ik moet het volgende differentieren: sqrt[4x-x^2].
Je moet met de kettingregel werken, dus dan krijg je
1/(2sqrt[4x-x^2]) * 4 - 2x * -2 leek mij. Uit het antwoord blijkt dat die laatste -2 niet meetelt, waarom niet? Ook op http://www.calc101.com/webMathematica/derivatives.jsp#topdoit doet hij niet mee.
En dan dnek je dat je differentieren na 3 jaar wel kunt... gek word ik er van
Ellendige opgave idd, maar had deze wel goed.
die wortel(4x-x^2) schrijf je als (4x-x^2)^0.5
En dan doe je die 0.5 naar voren en dat maal de afgeleide van wat er tussen de haken staat, dus:
0.5 * (4-2x) (4x-x^2)^-0.5
daarvan maak je dan:
2 - x (4x-x^2)^-0.5
uiteindelijk krijg je dan een breuk met onder de streep wortel(4x-x^2)
Snappie?
ps. bij differentieren met wortels ALTIJD van de wortel een ^0.5 maken, dan komt het (meestal) wel goed.
Later dan wel weer terugveranderen in een wortel als dat kan.
Ik heb een zeer gedetailleerde en overzichtelijke uitwerking van deze opdracht, moet ik hem plaatsen?
[ Bericht 5% gewijzigd door Mirri op 14-05-2007 23:01:55 ]
quote:volgens mij was dat de vraag waar ik er met lang kutten achter kwam dat het gewoon met de rekenmachine mochtOp maandag 14 mei 2007 20:30 schreef yootje het volgende:
[..]
Die inhoudsvraag erna snapte ik juist wel, alhoewel ik hem wle lastig vond.
wat mag je trouwens belachelijk veel met de rekenmachine trouwens? op SEs mochten we er ehelemaal niks mee, alles moest exact
quote:Nog gedetailleerder?Op maandag 14 mei 2007 22:48 schreef Mirri het volgende:
[..]
Ik heb een zeer gedetailleerde en overzichtelijke uitwerking van deze opdracht, moet ik hem plaatsen?
GRAAG
koffie
op vlucht tw378 vliegen kwaliteitscontroleurs van transworld mee.
Onder andere controleren ze de temperatuur van de koffie die de reizigers aan boord krijgen aangeboden.
Als norm geldt dat de koffietemperatuur moet zijn afgesteld op 70 C met een standaarddeviatie van 12 C.
Elke dag wordt van 30 kopjes de temperatuur gemeten.
Ga er van uit dat de temperatuur van de koffie normaal verdeeld is.
Is de gemiddelde temperatuur van deze 30 kopjes koffie te laag dan wordt de koffiemachine opnieuw afgesteld.
27. Wordt de machine opnieuw afgesteld bij een uitkomst van een gemiddelde koffietemperatuur van 65 C bij een significantieniveau van 5%?
De uitwerkingen zeggen dat je het met Z-Test (op de gr) moet doen, maar dat heb ik nog nooit gebruikt. Zijn er ook andere manieren?
Ik heb trouwens nu al die oefenopgave gemaakt. Zijn die veel makkelijker dan de echte examenopgaven of ben ik wel klaar als ik vandaag nog ff een examen maak? Al die oefenopgave kon ik wel prima maken
ExponentiŽle functie:
Ik weet wel hoe ik moet integreren, maar ik weet niet hoe ik de oppervlakte onder het lijnstuk AB moet vinden, en aan de hand van welke formule.
Who knows?
quote:Ok, dit is heel simpel, dit is hypothese toetsen. Goed dat je dit vraagt, want dit komt waarschijnlijk wel in het examen, doe je b1,2?Op dinsdag 15 mei 2007 09:45 schreef frank07 het volgende:
kansrekenen is echt n eitje maar ik liep gisteren bij de oefenopgave in de examenbundel toch bij 1 som vast... soms 27 op blz 66
koffie
op vlucht tw378 vliegen kwaliteitscontroleurs van transworld mee.
Onder andere controleren ze de temperatuur van de koffie die de reizigers aan boord krijgen aangeboden.
Als norm geldt dat de koffietemperatuur moet zijn afgesteld op 70 C met een standaarddeviatie van 12 C.
Elke dag wordt van 30 kopjes de temperatuur gemeten.
Ga er van uit dat de temperatuur van de koffie normaal verdeeld is.
Is de gemiddelde temperatuur van deze 30 kopjes koffie te laag dan wordt de koffiemachine opnieuw afgesteld.
27. Wordt de machine opnieuw afgesteld bij een uitkomst van een gemiddelde koffietemperatuur van 65 C bij een significantieniveau van 5%?
De uitwerkingen zeggen dat je het met Z-Test (op de gr) moet doen, maar dat heb ik nog nooit gebruikt. Zijn er ook andere manieren?
Ik heb trouwens nu al die oefenopgave gemaakt. Zijn die veel makkelijker dan de echte examenopgaven of ben ik wel klaar als ik vandaag nog ff een examen maak? Al die oefenopgave kon ik wel prima maken
H0 is het gemiddelde wat het zou moeten zijn, 70 C dus
H1 is < dan 70
Dan schrijf je in je schrift onder elkaar het volgende op:
lower
upper
u (gem.)
st.dev.
Daarachter schrijf je respectievelijk
- oneindig (oftewel -e^99 op je GR)
65
70
st.dev is geen 12 C, want het gaat om 30 koppen, dus wordt het 12/wortel30
Dan ga je naar district op je GR, en dan naar normalcdf en je vult alles in op de volgorde van dat rijtje met komma's er tussen, dat kun je wel toch? LET OP: het zou kunnen dat je u en st.dev moet omdraaien, hangt er van af of je casio of TI hebt.
Dus dit type je in: normalcdf(-e^99, 65, 70, 12/wortel30)
Als antwoord krijg je 0,011, dat is kleiner dan je significantieniveau 0.05 (5%), dus de H0 verwerpen!
Succes!
.
[ Bericht 0% gewijzigd door Mirri op 15-05-2007 10:57:46 ]
quote:Het lijnstuk AB is een rechte lijn. Invullen van de x-coordinaat in de formule van de kromme levert je de bijbehorende y-coordinaten op. Daarmee kan je de oppervlate onder lijn AB uitrekenen.Op dinsdag 15 mei 2007 10:34 schreef Juzme het volgende:
Mensen, ik heb ook een vraag. Examen 2005 Tijdvak 2
ExponentiŽle functie:
[afbeelding]
Ik weet wel hoe ik moet integreren, maar ik weet niet hoe ik de oppervlakte onder het lijnstuk AB moet vinden, en aan de hand van welke formule.
Who knows?
Het opp. onder de kromme moet je idd uitrekenen door te integreren. En deze trek je af van de opp. onder AB.
Klaar.
Preciezer: De kromme loopt van (0,1) tot (1, 1/e). Dus je oppervlakte is 1/e + 1/2*(1-1/e). (Eerste deel opp. rechthoek, tweede deel opp. driehoek).
Bedankt iig en volgens mij komt t wel goed met wiskunde (b1,2) bij mij..
quote:Dat gaat ver boven vwo-niveauhoe primitiveer je algabrarisch nou sqrt(4x-x^2)?
quote:Ja, ik dacht ook al, ik kom er maar niet uit,Op dinsdag 15 mei 2007 11:16 schreef GlowMouse het volgende:
Beetje asociaal als mensen vragen zowel hier als in dit topic stellen, en niet laten weten als de vraag ergens anders al beantwoord is.
[..]
Dat gaat ver boven vwo-niveau
quote:De opgave gaat verder in het examen..
We hebben de afgeleide bepaald:
-x+2 / wortel(4x-x^2) = 1 (deze vergelijking moet opgelost worden, want de r.c. van y = x is natuurlijk 1)
-x+2 = wortel(4x-x^2)
(-x+2)^2 = 4x-x^2
x^2 - 4x + 4 = 4x-x^2
x^2 - 4x + 4 - 4x +x^2 = 0
2x^2 - 8x + 4 = 0
x^2 - 4x + 2 = 0
En dan de ABC formule!!
a = 1, b = -4, c = 2
Dan krijg je x = 2 - wortel2
En x = 2 + wortel2, maar die kan niet
x = 0.6
Als je het uitschrijft zie je het vanzelf
quote:x = 2 - wortel2 is exact,Op dinsdag 15 mei 2007 11:33 schreef MaxC het volgende:
Is de ABC-formule exact?
x = 0.6 niet
btw; in de opgave staat bereken in 1 decimaal nauwkeurig
quote:Op zondag 20 mei 2007 17:12 schreef GlowMouse het volgende:
Stel je zou wel op het midden uitkomen. Pas de stelling dan eens omgekeerd toe. Neemt ABC als de kleine driehoek, en verleng het lijnstuk AB tot B'. Hoek ACB' zou dan 90 graden worden, tegenspraak.
quote:
[ Bericht 68% gewijzigd door Donnie_Darko op 20-05-2007 17:28:37 ]

Je zou wel op het midden uitkomen wanneer AB loodrecht zou staan op CM.
quote:Dit is voor VWO hoop ik, anders heb ik een druk paasweekendOp maandag 14 mei 2007 11:37 schreef yootje het volgende:
Hoi allemaal, ik ben bezig met het examen 2006-I, en er is maar iets waar ik niet uitkom.
Ik moet het volgende differentieren: sqrt[4x-x^2].
Je moet met de kettingregel werken, dus dan krijg je
1/(2sqrt[4x-x^2]) * 4 - 2x * -2 leek mij. Uit het antwoord blijkt dat die laatste -2 niet meetelt, waarom niet? Ook op http://www.calc101.com/webMathematica/derivatives.jsp#topdoit doet hij niet mee.
En dan dnek je dat je differentieren na 3 jaar wel kunt... gek word ik er van
quote:Ja, ik denk het wel. Ik doe niet al 3 jaar Havo iig (2)Op donderdag 24 mei 2007 15:01 schreef Lothario het volgende:
[..]
Dit is voor VWO hoop ik, anders heb ik een druk paasweekend
En differientieren op havo is niet zů moeilijk...
quote:klopt, tot logaritmische functies en dan houdt het ook wel op.Op donderdag 24 mei 2007 20:34 schreef Coastertommm het volgende:
[..]
Ja, ik denk het wel. Ik doe niet al 3 jaar Havo iig (2)
En differientieren op havo is niet zů moeilijk...
2) Formulekaart / papier... Wordt dat bij IEDEREEN gegeven?
3) Iemand nog een paar handige progjes voor A1,2?
(wiskunde A1 examen 2006-I)
Gemiddeld weegt een beschuit 8 gram. De standaardafwijking is 0,6. Hoe groot is de kans dat een beschuit meer dan 7,5 gram weegt?
Ik kom er echt even niet uit en voel me een beetje dom
quote:lower 7.5Op woensdag 30 mei 2007 10:29 schreef Sabinee het volgende:
Ik heb ook een wiskundevraag, ik weet dat ik iets heel gemakkelijks over het hoofd zie, maar kom er even niet uit wat...
(wiskunde A1 examen 2006-I)
Gemiddeld weegt een beschuit 8 gram. De standaardafwijking is 0,6. Hoe groot is de kans dat een beschuit meer dan 7,5 gram weegt?
Ik kom er echt even niet uit en voel me een beetje dom
upper oneindig, dat is e^99 dus
u (gem) 8
stand. afwijking: 0.6
Dat doe je in die volgorde in je rekenmachine bij normalcdf
In een post van mij een stukje hierboven zie je meer informatie
ik moet het volgende uitrekenen:
bereken de kans dat er precies 400 van de 1000 mensen op een bepaalde partij stemmen.
de kans hierop is 0,4.
ik vul in op m'n rekenmachine bij Stat, dist, binm, bpd:
X: 400
N: 1000
P: 0,4
dan krijg ik een Ma ERROR. ik doe vast iets fout, maar wat?
quote:Haha, verkeerde volgorde, het is n, p, XOp woensdag 30 mei 2007 10:41 schreef Reemy het volgende:
Bij wiskunde a1,2:
ik moet het volgende uitrekenen:
bereken de kans dat er precies 400 van de 1000 mensen op een bepaalde partij stemmen.
de kans hierop is 0,4.
ik vul in op m'n rekenmachine bij Stat, dist, binm, bpd:
X: 400
N: 1000
P: 0,4
dan krijg ik een Ma ERROR. ik doe vast iets fout, maar wat?
quote:?Op woensdag 30 mei 2007 10:43 schreef Mirri het volgende:
[..]
Haha, verkeerde volgorde, het is n, p, X
quote:nee, dat is de kans dat er op die partij word gestemd.Op woensdag 30 mei 2007 10:50 schreef GlowMouse het volgende:
Wat valt er nog te berekenen wanneer al gegeven is dat de kans op die gebeurtenis 0,4 is?
de kans op precies 400 stemmen is veel kleiner dan 0,4
quote:Ik denk dat de kans dat 1 gebeurtenis 0.4 is.Op woensdag 30 mei 2007 10:50 schreef GlowMouse het volgende:
Wat valt er nog te berekenen wanneer al gegeven is dat de kans op die gebeurtenis 0,4 is?
[ Bericht 0% gewijzigd door GlowMouse op 30-05-2007 10:59:39 ]
quote:hmm ik heb maar wiskunde a1,2 hoor:p wat je nu precies doet heb ik nog nooit gezienOp woensdag 30 mei 2007 10:54 schreef GlowMouse het volgende:
Ah, dan stond het er verkeerd. Het zou kunnen dat je rekenmachine niet kan omgaan met zulke grote aantallen. Je kunt dan een benadering maken met de normale verdeling. Het volstaat te berekenen P(399.5<X<400.5 | NV; mu=400, sigma=wortel(1000*0.4*(1-0.4))).
maar toch bedankt, denk dat m'n rekenmachine idd niet om kan gaan met de grote getallen
quote:n, het aantal tests (1000)
p, het aantal positieve uitgevallen kansen (400)
k, de kans dat het positief uitvalt (0,4) (of X, ook goed..)
Binompdf(1000, 400, 0,4) in de Texas GR
quote:Op zaterdag 26 mei 2007 16:38 schreef MrManiak het volgende:
1) WTF is WisForta?
2) Formulekaart / papier... Wordt dat bij IEDEREEN gegeven?
3) Iemand nog een paar handige progjes voor A1,2?
2) Bij ons heeft iedereen een formulekaart zelf (ik heb een gekopiŽerde
Als je normaal-waarschijnlijkheidspapier bedoelt, dat krijg je
3) nee
Dus X=0=Maart 2001 en dan is X12.2 dus april 2002 (naar boven afgerond) of gewoon maart 2002?