[Bèta wiskunde] Huiswerk- en vragentopic

Dat is niet de meest elegante manier nee.

Sorry, ik zie dat ik vergeten ben te noemen dat het om oneven getallen gaat. Oeps.... dus:

quote:

Bepaal het aantal oneven getallen tussen de 1000 en de 9999, zodat alle vier cijfers verschillen en ongelijk aan nul zijn.

quote:

Op maandag 4 juni 2012 21:36 schreef Amoeba het volgende:
Eerste getal is 8
Tweede 7
derde 6
vierde 4

8*7*6*5

En dan nog een nCr ertussen ofzoiets. Goor hoofdstuk

Eerste getal heeft negen mogelijkheden toch? Dan kom je op 9*8*7*6=3024 getallen. Maar dan moet je nog ergens iets doen om te corrigeren voor dubbeltellen volgens mij...

Als de getallen niet oneven hoeven te zijn, dan is het gewoon 9*8*7*6

quote:

Op maandag 4 juni 2012 21:40 schreef Amoeba het volgende:

[..]

Ohja, de 1 verwarde me. 9*8*7*5 (laatste getal moet dus oneven zijn)

Fout.

quote:

Op maandag 4 juni 2012 21:23 schreef Amoeba het volgende:

[..]

Noem je dit wel gemakkelijk dan.

Ik wed dat 90% van alle havo leerlingen hier de steek zouden laten vallen zodra je NOG een keer met de ABC formule aan de haal moet wanneer er al zo'n harde vergelijking x = 1+√17 staat.

Misschien is het wel aardig om iets over de achtergronden van het vraagstuk te vertellen, want er zijn natuurlijk meerdere manieren om het op te lossen.

Als je een tekening maakt, dan zie je vrij gemakkelijk dat er in totaal vier lijnen zijn die door het punt (1;1) gaan en de beide assen snijden zodanig dat de afstand van de snijpunten 4 bedraagt. En je kunt dat ook zien aan het stelsel

a² + b² = 16, a + b = ab,

want eliminatie van a of b levert dan een vierdegraadsvergelijking op. Maar omdat de vier mogelijke lijnen twee aan twee spiegelsymmetrisch liggen t.o.v. de lijn y = x, geldt dus voor elk gespiegeld lijnenpaar dat het product van de richtingscoëfficiënten gelijk is aan 1. En dat betekent dat we een wederkerige vergelijking van de vierde graad krijgen als we de richtingscoëfficiënt m van de lijn door (1;1) als variabele nemen. Nu hebben wederkerige vergelijkingen van even graad de prettige eigenschap dat je die door een substitutie (hier: m + 1/m = z) eenvoudig kunt herleiden tot een vergelijking waarvan de graad nog maar de helft van de oorspronkelijke bedraagt. En zo krijg je dan inderdaad ook een vierkantsvergelijking, waarvan de twee oplossingen aanleiding geven tot twee nieuwe vierkantsvergelijkingen. Heel vroeger stonden wederkerige vergelijkingen op het programma van het hoger middelbaar onderwijs, maar daaruit zijn ze ergens in de jaren '50 van de vorige eeuw verdwenen. Een beetje googelen leert dat ze wel in Vlaanderen kennelijk hier en daar nog op het programma staan.

Varianten van dit probleem staan ook bekend als het zogeheten ladderprobleem, zie bijvoorbeeld hier (waar de auteur duidelijk de theorie van de wederkerige vergelijkingen niet kent) en hier.

[ Bericht 0% gewijzigd door Riparius op 04-06-2012 22:27:44 ]

quote:

Op maandag 4 juni 2012 21:41 schreef thenxero het volgende:

[..]

Fout.

Ik zit me af te vragen of het niet gewoon 9*8*7*6*(5/9)is, maar dit lijkt me té makkelijk..

quote:

Op maandag 4 juni 2012 21:49 schreef Unsub het volgende:

[..]

Ik zit me af te vragen of het niet gewoon 9*8*7*6*(5/9)is, maar dit lijkt me té makkelijk..

Daar staat dus eigenlijk 8*7*6*5. Dat is het goede antwoord. Probeer het maar eens te beredeneren.

Als je eruit bent kunnen we het een stapje moeilijker maken:
Bepaal het aantal oneven getallen tussen de 1000 en 9999 zodat alle vier cijfers verschillen (en wel de waarde 0 aan mogen nemen).

Succes

quote:

Op maandag 4 juni 2012 21:55 schreef thenxero het volgende:

[..]

Daar staat dus eigenlijk 8*7*6*5. Dat is het goede antwoord. Probeer het maar eens te beredeneren.

Als je eruit bent kunnen we het een stapje moeilijker maken:
Bepaal het aantal oneven getallen tussen de 1000 en 9999 zodat alle vier cijfers verschillen (en wel de waarde 0 aan mogen nemen).

Succes

Oh ja
Nouja, als je het criterium van oneven weglaat, zijn er dus 9*8*7*6 verschillende getallen. Je hebt, als je 0 niet mee laat tellen, 4 verschillende even getallen van de 9, en 5 oneven. Dus vermenigvuldig ik met de 'kans' (slechte woordkeus, kom even niet op het juiste woord) op een oneven getal, dit geeft 9*8*7*6*(5/9), wat hetzelfde is als 8*7*6*5.

Ik geloof niet dat dit de volledige/juiste redenatie is, maar ik ga me nog even buigen over het volgende probleem

quote:

Op maandag 4 juni 2012 22:04 schreef Amoeba het volgende:

[..]

Deze meneer in artikel 2 stelt dat elke 'haast symmetrische vergelijking' (bij wijze van de rangschikking van coëfficiënten) met behulp van een substitutie valt te reduceren tot een kwadratische aangelegenheid. Hoe kom ik erachter (of beredeneer) wat deze substitutie is? Of is dit altijd x + 1/x?

Dat is inderdaad een standaard substitutie. Het is ook vrij gemakkelijk in te zien waarom dat zo is. Bij een wederkerige vergelijking van even graad kun je de wortels verdelen in paren α, 1/α, β, 1/β enz. waarvan het product steeds één is. Hebben we een wederkerig polynoom P(x) van even graad waarvan α en 1/α twee nulpunten zijn, dan bevat P(x) dus een factor

(x - α)(x - 1/α) = (x² - (α + 1/α)x + 1) = x∙((x + 1/x) - (α + 1/α))

Is dus P(x) een wederkerig polynoom van de graad n = 2k, dan heb je zo:

P(x) = x^k∙Q(z) met z = x + 1/x,

waarbij Q(z) een polynoom is van de graad k, dus de helft van de graad n van P(x). En aangezien x = 0 geen wortel is van P(x) = 0 kun je dan alle wortels van P(x) = 0 vinden door Q(z) = 0 op te lossen en voor elk nulpunt z van Q(z) de vergelijking x + 1/x = z oftewel x² - zx + 1 = 0 weer op te lossen naar x.

[ Bericht 0% gewijzigd door Riparius op 04-06-2012 22:38:44 ]

quote:

Op maandag 4 juni 2012 22:20 schreef Unsub het volgende:

[..]

Oh ja
Nouja, als je het criterium van oneven weglaat, zijn er dus 9*8*7*6 verschillende getallen. Je hebt, als je 0 niet mee laat tellen, 4 verschillende even getallen van de 9, en 5 oneven. Dus vermenigvuldig ik met de 'kans' (slechte woordkeus, kom even niet op het juiste woord) op een oneven getal, dit geeft 9*8*7*6*(5/9), wat hetzelfde is als 8*7*6*5.

Ik geloof niet dat dit de volledige/juiste redenatie is, maar ik ga me nog even buigen over het volgende probleem

Ik snap dat dat je idee was. Maar die redenering is niet echt waterdicht. Het is makkelijker om direct te beredeneren dat er 8*7*6*5 uitkomt.

quote:

Op maandag 4 juni 2012 21:55 schreef thenxero het volgende:

[..]

Daar staat dus eigenlijk 8*7*6*5. Dat is het goede antwoord. Probeer het maar eens te beredeneren.

Als je eruit bent kunnen we het een stapje moeilijker maken:
Bepaal het aantal oneven getallen tussen de 1000 en 9999 zodat alle vier cijfers verschillen (en wel de waarde 0 aan mogen nemen).

Succes

9*9*8*7/2 zeg ik zo even als eerste gedachte.

quote:

Op maandag 4 juni 2012 22:28 schreef thenxero het volgende:

[..]

Ik snap dat dat je idee was. Maar die redenering is niet echt waterdicht. Het is makkelijker om direct te beredeneren dat er 8*7*6*5 uitkomt.

Hier denk ik morgen nog even over na, zal morgenavond weer een keer posten

quote:

Op maandag 4 juni 2012 22:28 schreef thenxero het volgende:

[..]

Ik snap dat dat je idee was. Maar die redenering is niet echt waterdicht. Het is makkelijker om direct te beredeneren dat er 8*7*6*5 uitkomt.

Hoezo is die beredenering eigenlijk niet waterdicht? Je hebt, zonder de oneven restrictie, 9*8*7*6 keuzes gezien de andere restricties. Vervolgens selecteer je de oneven getallen er uit door alleen getallen met als laatste cijfer 1,3,5,7 of 9 mee te tellen, ofwel 5/9 van de mogelijke getallen die voldeden aan de eerdere restrictie (0 was geen keuze gezien de eerste restrictie).

quote:

Op dinsdag 5 juni 2012 00:14 schreef Physics het volgende:

[..]

Hoezo is die beredenering eigenlijk niet waterdicht? Je hebt, zonder de oneven restrictie, 9*8*7*6 keuzes gezien de andere restricties. Vervolgens selecteer je de oneven getallen er uit door alleen getallen met als laatste cijfer 1,3,5,7 of 9 mee te tellen, ofwel 5/9 van de mogelijke getallen die voldeden aan de eerdere restrictie (0 was geen keuze gezien de eerste restrictie).

Je redenering klopt niet, want als bijvoorbeeld de eerste drie cijfers alle drie oneven zijn, dan zijn er nog maar 2 mogelijkheden voor het laatste cijfer, en niet vijf zoals jij veronderstelt.

Ik heb een vraag over analyse/lagrange multipliers.

Bepaal de maximale afstand van een punt in de doorsnede van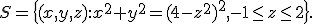 met het vlak y = 3 tot het punt (0, 0, 2).

Mijn poging:

Afstand is maximaal als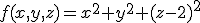 maximaal is.
S geeft als constraint: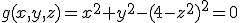
En het vlak y=3 geeft :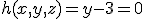

Nu kritieke punten van de Lagrange multiplier L bepalen.

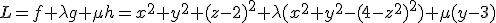
Dan moet gelden (partiele afgeleides):

1)
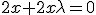
2)
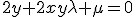
3)
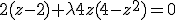
4)
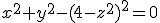
5)

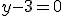
Dus y = 3.
Uit 1) volgt x = 0 of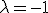
Als x = 0 kom ik keurig uit. ( (0,3,-1) geeft f = 18)
Als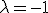 , dan krijg ik uit 3) een derdegraadsvergelijking voor z. Is dit niet te omzeilen? Ik heb vanalles geprobeerd met regels 3 en 4, en met f kleiner praten dan 18, maar ik zie het niet. Iemand een idee?

quote:

Op dinsdag 5 juni 2012 01:48 schreef Anoonumos het volgende:
Ik heb een vraag over analyse/lagrange multipliers.

Bepaal de maximale afstand van een punt in de doorsnede van met het vlak y = 3 tot het punt (0, 0, 2).

Mijn poging:

Afstand is maximaal als maximaal is.
S geeft als constraint:
En het vlak y=3 geeft :

Nu kritieke punten van de Lagrange multiplier L bepalen.

Dan moet gelden (partiele afgeleides):

1)
2)
3)
4)
5)

Dus y = 3.
Uit 1) volgt x = 0 of
Als x = 0 kom ik keurig uit. ( (0,3,-1) geeft f = 18)
Als , dan krijg ik uit 3) een derdegraadsvergelijking voor z. Is dit niet te omzeilen? Ik heb vanalles geprobeerd met regels 3 en 4, en met f kleiner praten dan 18, maar ik zie het niet. Iemand een idee?

Om te beginnen: ∂L/∂y = 2y + 2λy + μ

De oplossing van je vergelijking is echt heel eenvoudig, je ziet nl. over het hoofd dat z² - 4 = (z - 2)(z + 2) en dat je dus een factor (z - 2) buiten haakjes kunt halen. Voor λ = -1 hebben we:

2(z - 2) + 4z(z² - 4) = 0

en dus:

(z - 2)(2 + 4z(z + 2)) = 0

en dus:

(z - 2)(4z² + 8z + 2) = 0

Nu is de oplossing uiteraard eenvoudig, de wortels zijn:

z = 2 ∨z = -1 + ½√2 ∨z = -1 - ½√2

Dit komt verder niet mooi uit, het gezochte maximum van je f(x,y,z) wordt bereikt voor x = ½√(-3 + 20√2), y = 3, z = -1 + ½√2, en dit maximum bedraagt dan 71/4 + 2√2, maar dat mag je zelf even narekenen.

nvm.

[ Bericht 98% gewijzigd door Dale. op 05-06-2012 11:58:15 ]

Bedankt Riparius. Dat zag ik inderdaad over het hoofd. Het is nu gelukt en ik krijg dezelfde waarde.

Even een kort vraagje. Hoe los ik deze formule algebraïsch op: 8x - 2e^x = 0