ONZ Onzin voor je leven!
Vrolijkheid troef in dit lieve forum vol humor.
Welkom in ONZE Quiz. Het leukste quiz-topic in ONZ!
Hoe werkt het?
Iemand post een vraag, dat mag van alles zijn, maar het liefst wel een beetje triviaal en niet onmogelijk. Hints geven of filmpjes/plaatjes ter ondersteuning gebruiken is natuurlijk prima! Als iemand het juiste antwoord raadt (googlen is niet toegestaan en behoorlijk zielig), mag diegene het volgende vraagstuk verzinnen. Ook werken we met een stand. Raad jij het goede antwoord? Dan krijg je er één punt bij. Wanneer je een nieuw topic opent is het de bedoeling dat je de stand even netjes bij werkt en de laatst geposte vraag in de OP zet. Tevens dien je deze OP gewoon zo te laten staan. Vervelende users of trolls worden genegeerd.
Indien je geen spoiler gebruikt wanneer dit wordt gevraagd ben je automatisch gediskwalificeerd van deelname aan de vraag.
1: Fok-it: 140
2: EttovanBelgie: 92
3: Klaploper: 82
PowerLoungen: 81
deadprez: 72
houdjemond : 68
datismijnmening: 65
HPLC: 48
Targaryen: 45
Mani89: 44
mega-worstje: 41
TARDIS.:41
raptorix: 39
Kaneelstokje: 36
hetzalallemaalwel: 32
Mexicanobakker: 30
Pandaplint: 28
El_Matador: 26
Baconbus: 24
eliasbar: 23
MrBanaan1: 22
Dr.Mikey: 20
Johannes_V: 20
Boca_Raton: 20
Tanden68: 20
Aight1: 17
Remqo: 17
HaJee 16
GlennQuagmire : 16
ChevyCaprice: 16
Immerdebestebob: 16
jatochneetoch: 15
Fera: 15
dasorakel: 15
Guus_Geluk7: 14
Hawaii_Tim: 14
Ill-Skillz: 13
housesoftheholy: 12
Insomnia_: 11
Wolflegion: 10
Tassendief: 10
RingBewoner: 10
Holy_Goat:9
DjeDje: 9
Rockiejj: 8
Anosmos: 8
Elan: 8
Quyxz_: 7
AF: 7
LTVDK: 7
LompeHork 6
Noodgang: 6
Lt.Surge: 5
richolio: 5
KitKatChunky : 4
remlof: 4
PartyHard: 4
Pussyslayer: 3
ROADRUNN3R : 3
Moira: 3
Mooooortaxxje: 3
Flippieeeee: 3
ir.Relevant: 3
SebbeSwensje: 2
BazZz2b: 2
zerak: 2
Durmada:2
Dagoduck: 2
BarendWubboJagermansJansen: 2
D4v1D: 2
Hugecooll:2
Roceco: 2
Quotidien: 1
Dieseltank: 1
Vanillekwark: 1
appelen: 1
Gesloten: 1
Summer2bird: 1
Der_Mann:1
BlauweVinkjes: 1
Symphonic: 1
JimmyDean 1
Emotionele exclusiviteit monogamie-adept
Vergeten de TT te veranderen. Dan maar een vraag over Liechtenstein.
Liechtenstein is het op 5 na kleinste land ter wereld.
Noem alle 5 kleinere landen.
Antwoord nummer 5 is de winnaar.
Liechtenstein is het op 5 na kleinste land ter wereld.
Noem alle 5 kleinere landen.
Antwoord nummer 5 is de winnaar.
Emotionele exclusiviteit monogamie-adept
Vaticaanstad, San Marino en Monaco, de laatste weet ik zo snel niet, zal wel een of ander raar eiland in de Stille Oceaan zijn ofzo.quote:Op maandag 21 januari 2019 13:34 schreef Kaneelstokje het volgende:
Vergeten de TT te veranderen. Dan maar een vraag over Liechtenstein.
Liechtenstein is het op 5 na kleinste land ter wereld.
Noem alle 5 kleinere landen.
Antwoord nummer 5 is de winnaar.
Op maandag 24 augustus 2015 11:34 schreef Yasmin23 het volgende:
Als je maar genoeg moeite doet past alles.
_____
TV / Het post-apocalyptische/dystopische film topic
Als je maar genoeg moeite doet past alles.
_____
TV / Het post-apocalyptische/dystopische film topic
Alle 3 correct.quote:Op maandag 21 januari 2019 13:40 schreef LTVDK het volgende:
[..]
Vaticaanstad, San Marino en Monaco, de laatste weet ik zo snel niet, zal wel een of ander raar eiland in de Stille Oceaan zijn ofzo.
Nog 2 antwoorden.
Zijn idd beide eilandjes.
Emotionele exclusiviteit monogamie-adept
2de antwoord zit in de buurt.quote:
Ook geen idee, dus we gaan maar gokken op Barbados en Fiji
Emotionele exclusiviteit monogamie-adept
Cyprus
They wish to cure us. But I say to you, WE are the cure!
"WHAT IF YOU'RE RIGHT AND THEY'RE WRONG?"
R.I.P DTS.
"WHAT IF YOU'RE RIGHT AND THEY'RE WRONG?"
R.I.P DTS.
Correct, punt voor Bob.
Kan iemand de stand van vorige topic kopiëren? Zit mobiel en weet niet hoe en wat
Kan iemand de stand van vorige topic kopiëren? Zit mobiel en weet niet hoe en wat
Emotionele exclusiviteit monogamie-adept
1. Fok-it: 141quote:
Correct, punt voor Bob.
Kan iemand de stand van vorige topic kopiëren? Zit mobiel en weet niet hoe en wat
2: EttovanBelgie: 92
3: Klaploper: 82
PowerLoungen: 81
deadprez: 72
houdjemond : 68
datismijnmening: 65
HPLC: 52
Targaryen: 45
Mani89: 44
mega-worstje: 41
TARDIS.:41
Kaneelstokje: 39
raptorix: 39
hetzalallemaalwel: 32
Mexicanobakker: 30
Pandaplint: 28
El_Matador: 26
Baconbus: 24
eliasbar: 23
MrBanaan1: 22
Dr.Mikey: 20
Johannes_V: 20
Boca_Raton: 20
Tanden68: 20
Hawaii_Tim: 20 (+1?)
Immerdebestebob: 18
Aight1: 17
Remqo: 17
HaJee 16
GlennQuagmire : 16
ChevyCaprice: 16
jatochneetoch: 15
Fera: 15
dasorakel: 15
Guus_Geluk7: 14
Ill-Skillz: 13
housesoftheholy: 12
Insomnia_: 11
Wolflegion: 10
Tassendief: 10
RingBewoner: 10
Holy_Goat:9
DjeDje: 9
LTVDK: 8
Rockiejj: 8
Anosmos: 8
Elan: 8
Quyxz_: 7
AF: 7
LompeHork 6
Noodgang: 6
Lt.Surge: 5
richolio: 5
KitKatChunky : 4
remlof: 4
PartyHard: 4
Flippieeeeee: 5
Pussyslayer: 3
ROADRUNN3R : 3
Moira: 3
Mooooortaxxje: 4
ir.Relevant: 3
Quotidien: 3
SebbeSwensje: 2
Side Effect 2
BazZz2b: 2
zerak: 2
Durmada:2
Dagoduck: 2
BarendWubboJagermansJansen: 2
D4v1D: 2
Hugecooll:2
Roceco: 2
skysheriff: 2
Naatje_1: 2
Dieseltank: 1
Vanillekwark: 1
appelen: 1
Gesloten: 1
Summer2bird: 1
Der_Mann:1
BlauweVinkjes: 1
Symphonic: 1
JimmyDean 1
Driepink 1
Op maandag 24 augustus 2015 11:34 schreef Yasmin23 het volgende:
Als je maar genoeg moeite doet past alles.
_____
TV / Het post-apocalyptische/dystopische film topic
Als je maar genoeg moeite doet past alles.
_____
TV / Het post-apocalyptische/dystopische film topic
Is al met puntje erbij voor Bob overigens.
Op maandag 24 augustus 2015 11:34 schreef Yasmin23 het volgende:
Als je maar genoeg moeite doet past alles.
_____
TV / Het post-apocalyptische/dystopische film topic
Als je maar genoeg moeite doet past alles.
_____
TV / Het post-apocalyptische/dystopische film topic
Waar kennen we de afkortingen P.U.I.K.B.U.I.K., B.R.A.L.L.E.N.D.E.B.U.L.L.E.B.A.K en Z.W.E.R.F.D.O.D.O. van?
Specifiek graag.
Specifiek graag.
Dank je welquote:
Is al met puntje erbij voor Bob overigens.
Emotionele exclusiviteit monogamie-adept
quote:
[..]
Klinkt echt als afkortingen van de Jonge Woudlopers uit de Donald Duck
1. Fok-it: 141
2: EttovanBelgie: 92
3: Klaploper: 82
PowerLoungen: 81
deadprez: 72
houdjemond : 68
datismijnmening: 65
HPLC: 53
Targaryen: 45
Mani89: 44
mega-worstje: 41
TARDIS.:41
Kaneelstokje: 39
raptorix: 39
hetzalallemaalwel: 32
Mexicanobakker: 30
Pandaplint: 28
El_Matador: 26
Baconbus: 24
eliasbar: 23
MrBanaan1: 22
Dr.Mikey: 20
Johannes_V: 20
Boca_Raton: 20
Tanden68: 20
Hawaii_Tim: 20 (+1?)
Immerdebestebob: 18
Aight1: 17
Remqo: 17
HaJee 16
GlennQuagmire : 16
ChevyCaprice: 16
jatochneetoch: 15
Fera: 15
dasorakel: 15
Guus_Geluk7: 14
Ill-Skillz: 13
housesoftheholy: 12
Insomnia_: 11
Wolflegion: 10
Tassendief: 10
RingBewoner: 10
Holy_Goat:9
DjeDje: 9
LTVDK: 8
Rockiejj: 8
Anosmos: 8
Elan: 8
Quyxz_: 7
AF: 7
LompeHork 6
Noodgang: 6
Lt.Surge: 5
richolio: 5
KitKatChunky : 4
remlof: 4
PartyHard: 4
Flippieeeeee: 5
Pussyslayer: 3
ROADRUNN3R : 3
Moira: 3
Mooooortaxxje: 4
ir.Relevant: 3
Quotidien: 3
SebbeSwensje: 2
Side Effect 2
BazZz2b: 2
zerak: 2
Durmada:2
Dagoduck: 2
BarendWubboJagermansJansen: 2
D4v1D: 2
Hugecooll:2
Roceco: 2
skysheriff: 2
Naatje_1: 2
Dieseltank: 1
Vanillekwark: 1
appelen: 1
Gesloten: 1
Summer2bird: 1
Der_Mann:1
BlauweVinkjes: 1
Symphonic: 1
JimmyDean 1
Driepink 1
2: EttovanBelgie: 92
3: Klaploper: 82
PowerLoungen: 81
deadprez: 72
houdjemond : 68
datismijnmening: 65
HPLC: 53
Targaryen: 45
Mani89: 44
mega-worstje: 41
TARDIS.:41
Kaneelstokje: 39
raptorix: 39
hetzalallemaalwel: 32
Mexicanobakker: 30
Pandaplint: 28
El_Matador: 26
Baconbus: 24
eliasbar: 23
MrBanaan1: 22
Dr.Mikey: 20
Johannes_V: 20
Boca_Raton: 20
Tanden68: 20
Hawaii_Tim: 20 (+1?)
Immerdebestebob: 18
Aight1: 17
Remqo: 17
HaJee 16
GlennQuagmire : 16
ChevyCaprice: 16
jatochneetoch: 15
Fera: 15
dasorakel: 15
Guus_Geluk7: 14
Ill-Skillz: 13
housesoftheholy: 12
Insomnia_: 11
Wolflegion: 10
Tassendief: 10
RingBewoner: 10
Holy_Goat:9
DjeDje: 9
LTVDK: 8
Rockiejj: 8
Anosmos: 8
Elan: 8
Quyxz_: 7
AF: 7
LompeHork 6
Noodgang: 6
Lt.Surge: 5
richolio: 5
KitKatChunky : 4
remlof: 4
PartyHard: 4
Flippieeeeee: 5
Pussyslayer: 3
ROADRUNN3R : 3
Moira: 3
Mooooortaxxje: 4
ir.Relevant: 3
Quotidien: 3
SebbeSwensje: 2
Side Effect 2
BazZz2b: 2
zerak: 2
Durmada:2
Dagoduck: 2
BarendWubboJagermansJansen: 2
D4v1D: 2
Hugecooll:2
Roceco: 2
skysheriff: 2
Naatje_1: 2
Dieseltank: 1
Vanillekwark: 1
appelen: 1
Gesloten: 1
Summer2bird: 1
Der_Mann:1
BlauweVinkjes: 1
Symphonic: 1
JimmyDean 1
Driepink 1
Ln xquote:
Geef de afgeleiden van:
- f (x) = ex
- f (x) = ln x
X ln x
Klopt, die tweede is foutquote:Op maandag 21 januari 2019 14:24 schreef Immerdebestebob het volgende:
Correctie: e^x voor die eerste
Oeiquote:
[..]
Dat is meer dan integraal geloof ik
Ik voel me treurig. Dank je Hplc
ik moet ook vragen proberen te beantwoorden over hocus pocus pilatus pas en hamstersoortenquote:Op maandag 21 januari 2019 18:25 schreef Immerdebestebob het volgende:
Volgens mij is niet iedereen hooggeleid (en beta).
Ik zou niet eens weten wat het betekent, laat staan waar het op afleidquote:
Geef de afgeleiden van:
- f (x) = ex
- f (x) = ln x
Op maandag 24 augustus 2015 11:34 schreef Yasmin23 het volgende:
Als je maar genoeg moeite doet past alles.
_____
TV / Het post-apocalyptische/dystopische film topic
Als je maar genoeg moeite doet past alles.
_____
TV / Het post-apocalyptische/dystopische film topic
Ik weet het antwoord inmiddels, omdat het me irriteerde dat ik het niet meer wist. Heb nota bene dat Calculus-boek thuis staan.quote:
[..]
ik moet ook vragen proberen te beantwoorden over hocus pocus pilatus pas en hamstersoorten
Als je een plotje maakt met een mooie lijn er in, kan je met de afgeleide de helling van de lijn bepalen en met de integraal het gebied onder de lijn.quote:
[..]
Ik zou niet eens weten wat het betekent, laat staan waar het op afleid
Als je bijvoorbeeld y=2*x hebt, dan kan heb je dus een mooie lineaire lijn. De afgeleide is y = 2. Op elk punt is de helling hetzelfde, namelijk 2.
quote:
[..]
Als je een plotje maakt met een mooie lijn er in, kan je met de afgeleide de helling van de lijn bepalen en met de integraal het gebied onder de lijn.
Ik heb nog steeds geen flauw idee waar het over gaatquote:
Als je bijvoorbeeld y=2*x hebt, dan kan heb je dus een mooie lineaire lijn. De afgeleide is y = 2. Op elk punt is de helling hetzelfde, namelijk 2.
. Laten we het er maar op houden dat ik meer aanleg heb voor taal en creativiteit.
Op maandag 24 augustus 2015 11:34 schreef Yasmin23 het volgende:
Als je maar genoeg moeite doet past alles.
_____
TV / Het post-apocalyptische/dystopische film topic
Als je maar genoeg moeite doet past alles.
_____
TV / Het post-apocalyptische/dystopische film topic
quote:
[..]
[..]
Ik heb nog steeds geen flauw idee waar het over gaat
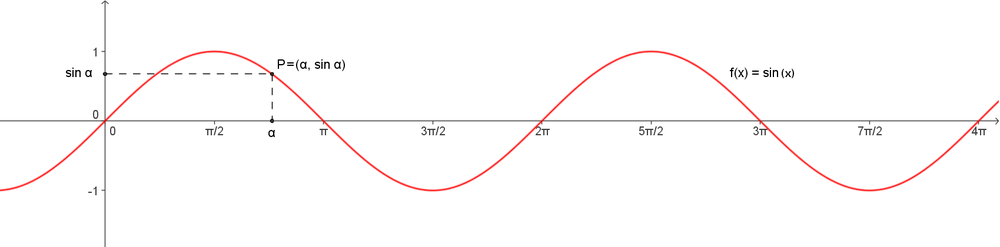
Stel je voor dat de rode lijn twee heuvels zijn. Als je beneden staat is het hellingspercentage '0' vlak dus en hetzelfde geldt voor de absolute top (je gaat niet omhoog of naar beneden). Halverwege is het hellingspercentage het hoogst. Dit alles kun je berekenen met de afgeleide.
De afgeleide van sinus x is overigens cosinus x
[ Bericht 2% gewijzigd door #ANONIEM op 21-01-2019 18:59:00 ]
Dit heb ik geloof ik allemaal verdrongen, ik heb destijds ook alle niet verplichte wiskunde laten vallen en ingeruild voor talen en geschiedenis en zulk soort vakkenquote:
[..]
[ afbeelding ]
Stel je voor dat de rode lijn twee heuvels zijn. Als je beneden staat is het hellingspercentage '0' vlak dus en hetzelfde geldt voor de absolute top (je gaat niet omhoog of naar beneden). Halverwege is het hellingspercentage het hoogst. Dit alles kun je berekenen met de afgeleide.
De afgeleide van sinus x is overigens cosinus x
Op maandag 24 augustus 2015 11:34 schreef Yasmin23 het volgende:
Als je maar genoeg moeite doet past alles.
_____
TV / Het post-apocalyptische/dystopische film topic
Als je maar genoeg moeite doet past alles.
_____
TV / Het post-apocalyptische/dystopische film topic
Nope, op f (x) = ln x bedoel je dan zeker?quote:Op maandag 21 januari 2019 19:38 schreef naatje_1 het volgende:
Ik heb wiskunde B gedaan, maar dat is echt een ellenlange tijd geleden. Ik ga gewoon ex gokken
dat was de enige die incorrect was vooralsnog, ja dusquote:
[..]
Nope, op f (x) = ln x bedoel je dan zeker?
ja nee, maar ln e heft elkaar wel op ja.quote:
[..]
dat was de enige die incorrect was vooralsnog, ja dus
Je hebt het punt:quote:
Volgens mij is niet iedereen hooggeleid (en beta).
1. Fok-it: 141
2: EttovanBelgie: 92
3: Klaploper: 82
PowerLoungen: 81
deadprez: 72
houdjemond : 68
datismijnmening: 65
HPLC: 53
Targaryen: 45
Mani89: 44
mega-worstje: 41
TARDIS.:41
Kaneelstokje: 39
raptorix: 39
hetzalallemaalwel: 32
Mexicanobakker: 30
Pandaplint: 28
El_Matador: 26
Baconbus: 24
eliasbar: 23
MrBanaan1: 22
Dr.Mikey: 20
Johannes_V: 20
Boca_Raton: 20
Tanden68: 20
Hawaii_Tim: 20 (+1?)
Immerdebestebob: 19
Aight1: 17
Remqo: 17
HaJee 16
GlennQuagmire : 16
ChevyCaprice: 16
jatochneetoch: 15
Fera: 15
dasorakel: 15
Guus_Geluk7: 14
Ill-Skillz: 13
housesoftheholy: 12
Insomnia_: 11
Wolflegion: 10
Tassendief: 10
RingBewoner: 10
Holy_Goat:9
DjeDje: 9
LTVDK: 8
Rockiejj: 8
Anosmos: 8
Elan: 8
Quyxz_: 7
AF: 7
LompeHork 6
Noodgang: 6
Lt.Surge: 5
richolio: 5
KitKatChunky : 4
remlof: 4
PartyHard: 4
Flippieeeeee: 5
Pussyslayer: 3
ROADRUNN3R : 3
Moira: 3
Mooooortaxxje: 4
ir.Relevant: 3
Quotidien: 3
SebbeSwensje: 2
Side Effect 2
BazZz2b: 2
zerak: 2
Durmada:2
Dagoduck: 2
BarendWubboJagermansJansen: 2
D4v1D: 2
Hugecooll:2
Roceco: 2
skysheriff: 2
Naatje_1: 2
Dieseltank: 1
Vanillekwark: 1
appelen: 1
Gesloten: 1
Summer2bird: 1
Der_Mann:1
BlauweVinkjes: 1
Symphonic: 1
JimmyDean 1
Driepink 1
Welke drie disciplines van het wielrennen beoefent Mathieu van der Poel? Hij is in elk van de drie Nederlands kampioen geworden.
Bonuspunt als je weet welke bekende wielrenner zijn opa was.
Bonuspunt als je weet welke bekende wielrenner zijn opa was.
