SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Kan iemand mij helpen
De laatste stap bij statement 1 (blauwe box) van:
3a = a(a2 + 3a +2) naar
a(a2 + 3a- 1)=0
Snap ik niet.
Overigens, voor de geïnteresseerde, het antwoord op de vraag is
De laatste stap bij statement 1 (blauwe box) van:
3a = a(a2 + 3a +2) naar
a(a2 + 3a- 1)=0
Snap ik niet.
Overigens, voor de geïnteresseerde, het antwoord op de vraag is
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.


Je trekt aan beide kanten 3a af. 2a - 3a = -1a, vandaar de -1 tussen de haakjes.
Als je eerst de haakjes wegwerkt, dan de 3a aftrekt, dan weer a buiten haakjes haalt, dan zie je 't wel denk ik?
[ Bericht 43% gewijzigd door #ANONIEM op 24-02-2016 16:54:21 ]
Als je eerst de haakjes wegwerkt, dan de 3a aftrekt, dan weer a buiten haakjes haalt, dan zie je 't wel denk ik?
[ Bericht 43% gewijzigd door #ANONIEM op 24-02-2016 16:54:21 ]


Het was ook wat logischer geweest als ze in de stap van de vierde naar de vijfde regel in die blauwe box eerst de 3a hadden afgetrokken en daarna pas de a buiten haakjes hadden gehaald.


ahh thanks, als je inderdaad de haakjes wegwerkt is het heel logisch.
Beetje raar dat ze dat dan niet deden voordat ze de formule in haakjes zette, het brengt zo extra verwarring.
Beetje raar dat ze dat dan niet deden voordat ze de formule in haakjes zette, het brengt zo extra verwarring.


Ik voer een two-sample t-test uit op een dataset. Nu wil ik deze dataset corrigeren met Bonforroni FDR. Ik rangschik de p-waarden die uit de test komen van laag naar hoog. Die p-waarden moet ik keer het totaal aantal metingen doen en dan delen door hun rang, maar hoe doe ik dat laatste? Ik werk in Matlab.
Gist is liefde, gist is leven. Vooral in een vagijn.


Hier zitten de slimmere bollebozen dus wie kan mij helpen met de uitleg en het antwoord?
5% van ...% van 22 is 11
Hij komt zo simpel over maar ik kom er gewoon niet uit

5% van ...% van 22 is 11
Hij komt zo simpel over maar ik kom er gewoon niet uit


quote:


Hoe bereken je ook alweer:
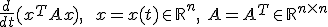
Als je schrijft:
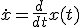
was het dan niet:
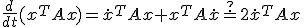
Maar ik ben de redenering even kwijt... Hoe zat het ook alweer?
En verandert er iets als A niet symmetrisch is?
Kon je niet een soort van ketting- en productregel toepassen?
Als je schrijft:
was het dan niet:
Maar ik ben de redenering even kwijt... Hoe zat het ook alweer?
En verandert er iets als A niet symmetrisch is?
Kon je niet een soort van ketting- en productregel toepassen?


quote:Op maandag 21 maart 2016 10:25 schreef Epps. het volgende:
Goedemorgen,
ik heb de mogelijkheid om via de Erasmus universiteit een wiskunde deficientecursus te volgen en zodoende toch toegelaten te worden tot de opleiding die ik wil volgen.
De cursus kost enkele honderden euro's en ik vroeg me af of het haalbaar is om de getoetste stof in twee maanden tijd te beheersen.
Heb zelf geen wiskunde meer gehad sinds de onderbouw dus mijn basiskennis is bijna 0,0.
Hieronder een voorbeeldtoets:
http://www.eur.nl/fileadm(...)au_2_versie_2014.pdf
Ik hoop dat jullie me hierbij willen helpen, indien jullie nog verdere vragen hebben kunnen jullie die uiteraard stellen in dit topic.


Als A niet symmetrisch is, dan geldt dat =-teken met het vraagteken erboven niet.quote:Op maandag 21 maart 2016 01:45 schreef Hahatsjoe het volgende:
Hoe bereken je ook alweer:
Als je schrijft:
was het dan niet:
Maar ik ben de redenering even kwijt... Hoe zat het ook alweer?
En verandert er iets als A niet symmetrisch is?
Kon je niet een soort van ketting- en productregel toepassen?


Echt niet? Want als ik het uitschrijf komt het er volgens mij gewoon uit. Het zijn uiteindelijk toch gewoon scalars en de volgorde waarin ik die vermenigvuldig dan wel optel maakt niet uit?quote:Op maandag 21 maart 2016 13:04 schreef thabit het volgende:
[..]
Als A niet symmetrisch is, dan geldt dat =-teken met het vraagteken erboven niet.


Voorbeeldje dan, waaruit blijkt dat je de symmetrie toch echt nodig hebt:
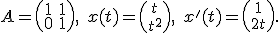
Dan is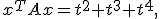 met als afgeleide
met als afgeleide 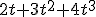 .
.
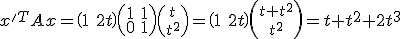 , en
, en 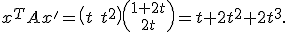
Dan is


Ohja. Zeer vriendelijk bedankt!quote:Op maandag 21 maart 2016 20:03 schreef thabit het volgende:
Voorbeeldje dan, waaruit blijkt dat je de symmetrie toch echt nodig hebt:
Dan ismet als afgeleide
.
, en


Hallo, is er iemand die me verder zou willen helpen?
Ik moet voor een verslag een "loglinear approximation" uitvoeren voor deze parabool rondom het punt gA*:
Nu heb ik de volgende stappen ondernomen waarbij ik op het juiste antwoord uitkom:
Ik moet voor een verslag een "loglinear approximation" uitvoeren voor deze parabool rondom het punt gA*:
Nu heb ik de volgende stappen ondernomen waarbij ik op het juiste antwoord uitkom:
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Ik heb alleen geen idee of mijn derivaties kloppen. Ook weet ik niet zeker of mijn vergelijkingen consistent zijn met deze grafiek, aangezien ik uitga van ggA en de grafiek van gA-punt. Zou er iemand zo vriendelijk willen zijn om te dubbel checken of dit inderdaad klopt?


Bij de eerste som:
Waarom is de oplossing 1/2pi + kpi en niet 1/2pi +2kpi?
En waarom nemen ze (2x+1/4pi)=-1/2pi + 2kpi niet mee?
Waarom is de oplossing 1/2pi + kpi en niet 1/2pi +2kpi?
En waarom nemen ze (2x+1/4pi)=-1/2pi + 2kpi niet mee?


Omdat cos(u) = 0 geldt voor u = (1/2)*pi + k*pi, waar k wordt gebruikt om veelvouden van pi aan te geven.quote:Op woensdag 30 maart 2016 12:08 schreef Goldenrush het volgende:
Waarom is de oplossing 1/2pi + kpi en niet 1/2pi +2kpi?
cos(u) = 0 geldt namelijk voor u=(1/2)*pi+pi, u=(1/2)*pi+2*pi, u=(1/2)*pi+3*pi, etc.
Kijk maar naar https://www.google.nl/sea(...)ceid=chrome&ie=UTF-8
Je kan voor k dus elke integer kiezen, niet enkel de even getallen: 2,4,6, etc.
[ Bericht 11% gewijzigd door ulq op 30-03-2016 15:35:15 ]


Denk aan de eenheidscirkel: de cosinus van een rotatiehoek is per definitie de x-coördinaat van het beeldpunt van (1; 0) bij rotatie om de oorsprong over die hoek. Zie ook hier.quote:Op woensdag 30 maart 2016 12:08 schreef Goldenrush het volgende:
Bij de eerste som:
[ afbeelding ]
Waarom is de oplossing 1/2pi + kpi en niet 1/2pi +2kpi?
Welnu, als je het startpunt (1; 0) over ½π rad om de oorsprong roteert, dan kom je uit in het punt (0; 1) en de x-coördinaat van dat punt - en daarmee de cosinus van ½π - is dus inderdaad 0. Maar als je nu vervolgens nog over een geheel aantal halve slagen in tegenwijzerzin of in wijzerzin rond de oorsprong roteert, dan kom je óf weer uit op het punt (0;1) óf op het punt (0;−1) en ook dan is de x-coördinaat van het beeldpunt - en dus de cosinus - weer gelijk aan 0. Dus is
cos(2x + ¼π) = 0
equivalent met
2x + ¼π = ½π + kπ, k ∈ ℤ
Dat zou ook kunnen, maar is hier minder handig. Je kunt bedenken dat de cosinus van ½π gelijk is aan nul, zodatquote:En waarom nemen ze (2x+1/4pi)=-1/2pi + 2kpi niet mee?
cos(2x + ¼π) = 0
equivalent is met
cos(2x + ¼π) = cos(½π)
Nu zijn de cosinussen van twee (rotatie)hoeken gelijk als die (rotatie)hoeken hetzij aan elkaar gelijk zijn, hetzij elkaars tegengestelde zijn, afgezien van een geheel veelvoud van 2π, dus
cos α = cos β ⇔ α = β + k·2π ∨ α = −β + k·2π, k ∈ ℤ
zodat
cos(2x + ¼π) = cos(½π)
dus equivalent is met
2x + ¼π = ½π + 2kπ ∨ 2x + ¼π = −½π + 2kπ, k ∈ ℤ
en dit geeft
x = ⅛π + kπ ∨ x = −⅜π + kπ, k ∈ ℤ
Maar nu kun je bedenken dat het verschil tussen een rotatie over (1/8)·π rad en een rotatie over (−3/8)·π rad een rotatie is over ½π rad, en dat is de helft van π rad, zodat we de beide deeloplossingen hier samen kunnen voegen en de volledige oplossing dus eenvoudiger kunnen schrijven als
x = ⅛π + k·½π, k ∈ ℤ
Dit is uiteraard precies hetzelfde resultaat, maar je ziet nu dat het handiger is om gelijk te bedenken dat een cosinus van een rotatiehoek gelijk is aan nul als die rotatiehoek gelijk is aan ½π rad plus een geheel veelvoud van π rad.


Aha, ik vond het al zo raar, ik gebruikte cos(2x + ¼π) = cos(½π) namelijk! Eerste had ik wel bedacht maar ik vond het zo raar dat die andere methode niet werkte. Maar die oplossingen kan je samenvoegen dus.Heel erg bedankt!quote:Op woensdag 30 maart 2016 19:40 schreef Riparius het volgende:
[..]
Denk aan de eenheidscirkel: de cosinus van een rotatiehoek is per definitie de x-coördinaat van het beeldpunt van (1; 0) bij rotatie om de oorsprong over die hoek. Zie ook hier.
Welnu, als je het startpunt (1; 0) over ½π rad om de oorsprong roteert, dan kom je uit in het punt (0; 1) en de x-coördinaat van dat punt - en daarmee de cosinus van ½π - is dus inderdaad 0. Maar als je nu vervolgens nog over een geheel aantal halve slagen in tegenwijzerzin of in wijzerzin rond de oorsprong roteert, dan kom je óf weer uit op het punt (0;1) óf op het punt (0;−1) en ook dan is de x-coördinaat van het beeldpunt - en dus de cosinus - weer gelijk aan 0. Dus is
cos(2x + ¼π) = 0
equivalent met
2x + ¼π = ½π + kπ, k ∈ ℤ
[..]
Dat zou ook kunnen, maar is hier minder handig. Je kunt bedenken dat de cosinus van ½π gelijk is aan nul, zodat
cos(2x + ¼π) = 0
equivalent is met
cos(2x + ¼π) = cos(½π)
Nu zijn de cosinussen van twee (rotatie)hoeken gelijk als die (rotatie)hoeken hetzij aan elkaar gelijk zijn, hetzij elkaars tegengestelde zijn, afgezien van een geheel veelvoud van 2π, dus
cos α = cos β ⇔ α = β + k·2π ∨ α = −β + k·2π, k ∈ ℤ
zodat
cos(2x + ¼π) = cos(½π)
dus equivalent is met
2x + ¼π = ½π + 2kπ ∨ 2x + ¼π = −½π + 2kπ, k ∈ ℤ
en dit geeft
x = ⅛π + kπ ∨ x = −⅜π + kπ, k ∈ ℤ
Maar nu kun je bedenken dat het verschil tussen een rotatie over (1/8)·π rad en een rotatie over (−3/8)·π rad een rotatie is over ½π rad, en dat is de helft van π rad, zodat we de beide deeloplossingen hier samen kunnen voegen en de volledige oplossing dus eenvoudiger kunnen schrijven als
x = ⅛π + k·½π, k ∈ ℤ
Dit is uiteraard precies hetzelfde resultaat, maar je ziet nu dat het handiger is om gelijk te bedenken dat een cosinus van een rotatiehoek gelijk is aan nul als die rotatiehoek gelijk is aan ½π rad plus een geheel veelvoud van π rad.


Ik heb een vraagstuk waar ik niet uitkom:
Een bal rolt over een veld met een beginsnelheid op tijdstip x=0s van 8m/s. Door wrijving krijgt de bal een vertraging van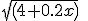 . Hoe ver rolt de bal?
. Hoe ver rolt de bal?
Ik heb voor de snelheid de formule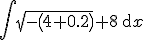 opgesteld.
opgesteld.
Hieruit haal ik V=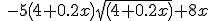
Deze zou ik dan toch gelijk moeten stellen aan 0? Omdat als de bal tot stilstand is gekomen de snelheid 0 is. Zodat ik de tijd (x) weet en deze in kan vullen in de formule voor de afgelegde weg.
[ Bericht 0% gewijzigd door Boarderzip op 02-04-2016 16:09:56 ]
Een bal rolt over een veld met een beginsnelheid op tijdstip x=0s van 8m/s. Door wrijving krijgt de bal een vertraging van
Ik heb voor de snelheid de formule
Hieruit haal ik V=
Deze zou ik dan toch gelijk moeten stellen aan 0? Omdat als de bal tot stilstand is gekomen de snelheid 0 is. Zodat ik de tijd (x) weet en deze in kan vullen in de formule voor de afgelegde weg.
[ Bericht 0% gewijzigd door Boarderzip op 02-04-2016 16:09:56 ]


Geef indien mogelijk eens een scan van de originele opgave. Je uitdrukking voor de vertraging is wel heel merkwaadig. En in welke eenheid is die vertraging uitgedrukt?quote:Op zaterdag 2 april 2016 14:00 schreef Boarderzip het volgende:
Ik heb een vraagstuk waar ik niet uitkom:
Een bal rolt over een veld met een beginsnelheid op tijdstip x=0s van 8m/s. Door wrijving krijgt de bal een vertraging van. Hoe ver rolt de bal?
Als de beginsnelheid 8 m·s−1 bedraagt en de vertraging is bijvoorbeeld 2 m·s−2 dan is de bal na 8 m·s−1 : 2 m·s−2 = 4 seconden tot stilstand gekomen.
[ Bericht 0% gewijzigd door Riparius op 02-04-2016 15:36:13 ]


Ik zie nu ook dat ik in de formule voor de vertraging de x vergeten was te noteren.quote:Op zaterdag 2 april 2016 15:29 schreef Riparius het volgende:
[..]
Geef indien mogelijk eens een scan van de originele opgave. Je uitdrukking voor de vertraging is wel heel merkwaadig. En in welke eenheid is die vertraging uitgedrukt?
Als de beginsnelheid 8 m·s−1 bedraagt en de vertraging is bijvoorbeeld 2 m·s−2 dan is de bal na 8 m·s−1 : 2 m·s−2 = 4 seconden tot stilstand gekomen.
Dit is de originele opgave, nummer 4:


Nee, de opgave gebruikt de letter t voor de tijd en dan moet je daar niet een x van maken.quote:Op zaterdag 2 april 2016 16:13 schreef Boarderzip het volgende:
Ik zie nu ook dat ik in de formule voor de vertraging de x vergeten was te noteren.
Geven we de snelheid (velocitas) op tijdstip t aan met v(t) en de versnelling (acceleratio) op tijdstip t met a(t) dan geldt
en dus
zodat
Nu is gegeven dat
en
zodat we dus hebben
Verder hebben we
en daarmee krijgen we
Nu moeten we bepalen voor welke waarde van t geldt v(t) = 0 en dan vinden we
De afstand die de bal heeft afgelegd vanaf het tijdstip t = 0 tot het moment dat de bal tot stilstand is gekomen op het tijdstip t = 5(10,42/3 − 4) vinden we nu door v(t) te integreren over het interval [0, 5(10,42/3 − 4)] en deze afstand bedraagt dus
oftewel ca. 15,51 meter (check).
[ Bericht 26% gewijzigd door Riparius op 03-04-2016 02:20:31 ]


Heel hartelijk dankquote:Op zaterdag 2 april 2016 16:58 schreef Riparius het volgende:
[..]
Nee, de opgave gebruikt de letter t voor de tijd en dan moet je daar niet een x van maken.
Geven we de snelheid (velocitas) op tijdstip t aan met v(t) en de versnelling (acceleratio) op tijdstip t met a(t) dan geldt
en dus
zodat
Nu is gegeven dat
en
zodat we dus hebben
Verder hebben we
en daarmee krijgen we
Nu moeten we bepalen voor welke waarde van t geldt v(t) = 0 en dan vinden we
De afstand die de bal heeft afgelegd vanaf het tijdstip t = 0 tot het moment dat de bal tot stilstand is gekomen op het tijdstip t = 5(10,42/3 − 4) vinden we nu door v(t) te integreren over het interval [0, 5(10,42/3 − 4)] en deze afstand bedraagt dus
oftewel ca. 15,51 meter (check).


quote:Op zondag 3 april 2016 16:07 schreef Boarderzip het volgende:
[..]
Heel hartelijk dankhet is me compleet duidelijk hoe je de som opbouwt, echter zie ik alleen nog niet hoe je de waarde van t berekent op v=0? Met behulp van een grafische rekenmachine krijg ik de juiste waarden voor t gevonden, maar op de hand krijg ik hem niet uitgewerkt.
geeft
Beide leden vermenigvuldigen met 3/10 geeft
Nu beide leden verheffen tot de macht 2/3 en je hebt
De rest kun je nu zelf wel. Overigens is 10,42/3 lastig met de hand uit te rekenen (c.q. te benaderen). Met een (gewone) rekenmachine is dat uiteraard geen probleem.
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |




