SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Niet van mijquote:Op donderdag 15 mei 2014 19:42 schreef Super-B het volgende:
[..]
Spannend hoor. Maandag de toets en dan is iedereen in dit topic van ons verlost!
Ik doe dit op vrijwillige basis, geen toetsen oid 
Dat denken ze. Moet je volgend schooljaar is opletten.quote:
[..]
Spannend hoor. Maandag de toets en dan is iedereen in dit topic van ons verlost!
Maar zonder gein, les van een docent gaat dan een stuk beter werken dan zelfstudie
Ga dan meteen ook wat colleges Nederlands volgen.quote:Op donderdag 15 mei 2014 20:19 schreef nodig het volgende:
[..]
Dat denken ze. Moet je volgend schooljaar is opletten.
Maar zonder gein, les van een docent gaat dan een stuk beter werken dan zelfstudie
Is misschien wel nuttig jaquote:
[..]
Ga dan meteen ook wat colleges Nederlands volgen.
Even iets geheel anders, ben jij een beetje bedreven in object geörienteerd programmeren (JAVA)? Concreter, ik heb literatuur nodig waar kort en bondig wordt uitgelegd hoe de structuur van OO programmeren nu in elkaar steekt.quote:
[..]
Ga dan meteen ook wat colleges Nederlands volgen.
Fervent tegenstander van het korps lasergamers.
Ik had je vraag al gezien, en ik heb wat ervaring met OO programmeren, maar dan in Pascal en Borland Delphi, niet met Java, sorry. Ik houd trouwens sowieso niet erg van de syntaxis van C(++) en aanverwante talen, veel te rommelig. Kernighan en Ritchie zijn niet my cup of tea. Wirth wel uiteraard.quote:Op donderdag 15 mei 2014 20:57 schreef Amoeba het volgende:
[..]
Even iets geheel anders, ben jij een beetje bedreven in object geörienteerd programmeren (JAVA)? Concreter, ik heb literatuur nodig waar kort en bondig wordt uitgelegd hoe de structuur van OO programmeren nu in elkaar steekt.
Allemaal eigenlijk.. Op de opgaven cos, sin, arcsin etc na (geen examenstof).quote:
[..]
De uitleg op blz. 179 lijkt me volstrekt helder. Echter, wat er allemaal wordt beweerd op blz. 177 van de PDF waar je naar linkt klopt niet. Hier is het nodige mis gegaan met de typografie, en Van de Craats introduceert hier ook nog eens ongebruikelijke termen. Wat hij monotoon stijgend noemt heet gewoonlijk strict monotoon stijgend en wat hij monotoon niet-dalend noemt heet gewoonlijk monotoon stijgend. Ik heb zelf overigens een volledige PDF waarin de typografische missers niet voorkomen. Ik weet niet of dit elders in het boek ook het geval is, maar het toont wel aan dat je niet kunt vertrouwen op de uitgeklede 'gratis' internetversie van het boek. Maar geef even het nummer van de opgave waar je problemen mee hebt.
Ik snap niet hoe ik het moet doen.
Kies één opgave uit, dan kan ik die even met je doornemen.quote:
[..]
Allemaal eigenlijk.. Op de opgaven cos, sin, arcsin etc na (geen examenstof).
Ik snap niet hoe ik het moet doen.
20.42 a & b kies ik.quote:
[..]
Kies één opgave uit, dan kan ik die even met je doornemen.
Opgave 20.42a.quote:
f(x) = xex
Afgeleide bepalen (met behulp van de productregel) geeft
f'(x) = 1·ex + x·ex = (x+1)·ex
Nu de nulpunten bepalen van de afgeleide f'(x). Hiervoor moet je je realiseren dat een e-macht nooit nul kan zijn. De afgeleide kan dus alleen nul zijn als de andere factor (x+1) nul is, en dat is het geval als
x = −1
Nu willen we weten of de functie f bij x = −1 een lokaal minimum of een lokaal maximum aanneemt, of wellicht geen van beide. Daarvoor kun je de tweede afgeleide bepalen en dan kijken naar het teken van f''(−1), maar hier is het ook eenvoudig te zien aan f'(x) = (x+1)·ex. De e-macht is immers altijd positief (voor elke reële x), zodat we zien dat f'(x) wisselt van negatief naar positief bij x = −1. En dat betekent dat de functie f een lokaal minimum moet hebben bij x = − 1. De waarde van dit locale minimum is f(−1) = −e−1.
Hier zie je een grafiekje van zowel f (in rood) als de afgeleide f' (in blauw). Je ziet hier heel mooi dat de curve van f' de x-as snijdt in het punt (−1; 0) en dat f bij x = − 1 inderdaad een minimum aanneemt. We weten (en zien ook in de grafiek) dat het lokale minimum tevens een globaal minimum is, want de functiewaarde f(x) daalt immers voor elke x < −1 en stijgt voor elke x > −1. Je ziet hier trouwens ook dat zowel de grafiek van f als de grafiek van f' een horizontale asymptoot y = 0 heeft. Dat komt, eenvoudig gezegd, omdat ex als we x steeds negatiever laten worden veel sneller naar nul toe gaat dan de absolute waarden van x en (x + 1) toe nemen, zodat de producten van ex met x en (x+1), en daarmee f(x) en f'(x), naar nul toe gaan voor x → − ∞.
Nu zelf maar even opgave 20.42b proberen.
Shit.. mijn boek is anders dan de internetversie.. Ik bedoelde: 20.39 a... Maar goed even lezen.quote:
[..]
Opgave 20.42a.
f(x) = xex
Afgeleide bepalen (met behulp van de productregel) geeft
f'(x) = 1·ex + x·ex = (x+1)·ex
Nu de nulpunten bepalen van de afgeleide f'(x). Hiervoor moet je je realiseren dat een e-macht nooit nul kan zijn. De afgeleide kan dus alleen nul zijn als de andere factor (x+1) nul is, en dat is het geval als
x = −1
Nu willen we weten of de functie f bij x = −1 een lokaal minimum of een lokaal maximum aanneemt, of wellicht geen van beide. Daarvoor kun je de tweede afgeleide bepalen en dan kijken naar het teken van f''(−1), maar hier is het ook eenvoudig te zien aan f'(x) = (x+1)·ex. De e-macht is immers altijd positief (voor elke reële x), zodat we zien dat f'(x) wisselt van negatief naar positief bij x = −1. En dat betekent dat de functie f een lokaal minimum moet hebben bij x = − 1. De waarde van dit locale minimum is f(−1) = −e−1.
[ afbeelding ]
Hier zie je een grafiekje van zowel f (in rood) als de afgeleide f' (in blauw). Je ziet hier heel mooi dat de curve van f' de x-as snijdt in het punt (−1; 0) en dat f bij x = − 1 inderdaad een minimum aanneemt. We weten (en zien ook in de grafiek) dat het lokale minimum tevens een globaal minimum is, want de functiewaarde f(x) daalt immers voor elke x < −1 en stijgt voor elke x > −1. Je ziet hier trouwens ook dat zowel de grafiek van f als de grafiek van f' een horizontale asymptoot y = 0 heeft. Dat komt, eenvoudig gezegd, omdat ex als we x steeds negatiever laten worden veel sneller naar nul toe gaat dan de absolute waarden van x en (x + 1) toe nemen, zodat de producten van ex met x en (x+1), en daarmee f(x) en f'(x), naar nul toe gaan voor x → − ∞.
Nu zelf maar even opgave 20.42b proberen.
EDIT: 20.39 c is mij gelukt... te maken, blijf toch hangen bij 20.39 a en b, ondanks dat ik jouw methodiek geheel snap!
Dankjewel voor je heldere uitleg de afgelopen dagen en weken. Ik heb veel gehad aan je uitleg aan mij, Nodig & Rustcohle.
Geef even aan welke functies bij opgave 20.39a en 20.39b worden gegeven. In beide versies van het boek die ik (als PDF) tot mijn beschikking heb is dat x3 − x resp. x4 − 2x2.quote:
[..]
Shit.. mijn boek is anders dan de internetversie.. Ik bedoelde: 20.39 a... Maar goed even lezen.
EDIT: 20.39 c is mij gelukt... te maken, blijf toch hangen bij 20.39 a en b, ondanks dat ik jouw methodiek geheel snap!
Dankjewel voor je heldere uitleg de afgelopen dagen en weken. Ik heb veel gehad aan je uitleg aan mij, Nodig & Rustcohle.
De methode snap ik. Bij x³-x kom ik uit op √1/3 en -√1/3, maar ik snap niet hoe je het kan schrijven tot 1/3√3 en -1/3√3.quote:
[..]
Geef even aan welke functies bij opgave 20.39a en 20.39b worden gegeven. In beide versies van het boek die ik (als PDF) tot mijn beschikking heb is dat x3 − x resp. x4 − 2x2.
Bij x^4 - 2x² maar bij de tekening zie ik de globale minima's en het lokale maximum niet... Het is een dalparabool in mijn tekening. Wanneer is er overigens sprake van een globale minimum en wanneer van een lokale minimum? Ik dacht dat er alleen maar 1 globale minimum in een grafiek mogelijk was (het laagste punt in een grafiek).
Voor zover ik weet:
lokaal minimum: één van de laagste punten
globaal minimum: allerlaagste punt in de grafiek
Waar ik echt moeite mee heb is:
20.41 a & b en 20.42 e qua opgaven.
Met 20.39 a is het probleem de schrijfwijze, zoals eerder gezegd, en bij 20.39 b is het probleem dat de grafiek niet overeenkomt met het antwoord (althans bij mij..). Het antwoord heb ik overigens wel goed.
Herleiding van uitdrukkingen met wortels: hiervoor bestaan rekenregels, die Van de Craats ook behandelt in hoofdstuk 3 Machten en wortels. De rekenregels voor wortels zijn nauw verwant met de rekenregels voor machten, omdat je elke wortel immers ook kunt schrijven als een macht met een gebroken (niet gehele) exponent. Verder spelen de rekenregels voor het werken met breuken een rol bij het herleiden van uitdrukkingen met wortels. De waarde van een breuk verandert bijvoorbeeld niet als je teller en noemer met hetzelfde getal (ongelijk nul) vermenigvuldigt, of door hetzelfde getal (ongelijk nul) deelt. Je hebtquote:
[..]
De methode snap ik. Bij x³-x kom ik uit op √1/3 en -√1/3, maar ik snap niet hoe je het kan schrijven tot 1/3√3 en -1/3√3.
Dat is natuurlijk niet waar. Je moet niet elke curve die een beetje op een parabool lijkt een parabool noemen. Dit is geen kwadratische functie maar een vierdemachts polynoomfunctie en de grafiek kan dan ook geen parabool zijn.quote:Bij x^4 - 2x² maar bij de tekening zie ik de globale minima en het lokale maximum niet... Het is een dalparabool in mijn tekening.
Nee, je kunt toch méér dan één punt hebben in een grafiek met dezelfde laagste functiewaarde?quote:Wanneer is er overigens sprake van een globaal minimum en wanneer van een lokaal minimum? Ik dacht dat er alleen maar 1 globaal minimum in een grafiek mogelijk was (het laagste punt in een grafiek).
Ja, maar wat nu wanneer dat zelfde laagste punt voor twee verschillende waarden van x wordt bereikt? Dan heb je toch twee laagste punten?quote:Voor zover ik weet:
lokaal minimum: één van de laagste punten
globaal minimum: allerlaagste punt in de grafiek
Heb je de grafiek met pen en papier geschetst of door een computerprogramma laten tekenen?quote:Waar ik echt moeite mee heb is:
20.41 a & b en 20.42 e qua opgaven.
Met 20.39 a is het probleem de schrijfwijze, zoals eerder gezegd, en bij 20.39 b is het probleem dat de grafiek niet overeenkomt met het antwoord (althans bij mij..). Het antwoord heb ik overigens wel goed.
Hoe zou je hier de afgeleide ookal weer bepalen met de dy/dx methode?quote:
[..]
Opgave 20.42a.
f(x) = xex
Afgeleide bepalen (met behulp van de productregel) geeft
f'(x) = 1·ex + x·ex = (x+1)·ex
Nu de nulpunten bepalen van de afgeleide f'(x). Hiervoor moet je je realiseren dat een e-macht nooit nul kan zijn. De afgeleide kan dus alleen nul zijn als de andere factor (x+1) nul is, en dat is het geval als
x = −1
Nu willen we weten of de functie f bij x = −1 een lokaal minimum of een lokaal maximum aanneemt, of wellicht geen van beide. Daarvoor kun je de tweede afgeleide bepalen en dan kijken naar het teken van f''(−1), maar hier is het ook eenvoudig te zien aan f'(x) = (x+1)·ex. De e-macht is immers altijd positief (voor elke reële x), zodat we zien dat f'(x) wisselt van negatief naar positief bij x = −1. En dat betekent dat de functie f een lokaal minimum moet hebben bij x = − 1. De waarde van dit locale minimum is f(−1) = −e−1.
[ afbeelding ]
Hier zie je een grafiekje van zowel f (in rood) als de afgeleide f' (in blauw). Je ziet hier heel mooi dat de curve van f' de x-as snijdt in het punt (−1; 0) en dat f bij x = − 1 inderdaad een minimum aanneemt. We weten (en zien ook in de grafiek) dat het lokale minimum tevens een globaal minimum is, want de functiewaarde f(x) daalt immers voor elke x < −1 en stijgt voor elke x > −1. Je ziet hier trouwens ook dat zowel de grafiek van f als de grafiek van f' een horizontale asymptoot y = 0 heeft. Dat komt, eenvoudig gezegd, omdat ex als we x steeds negatiever laten worden veel sneller naar nul toe gaat dan de absolute waarden van x en (x + 1) toe nemen, zodat de producten van ex met x en (x+1), en daarmee f(x) en f'(x), naar nul toe gaan voor x → − ∞.
Nu zelf maar even opgave 20.42b proberen.
Hoe bedoel je? In de notatie van Leibniz kun je schrijvenquote:
[..]
Hoe zou je hier de afgeleide ookal weer bepalen met de dy/dx methode?
d(x·ex)/dx = (dx/dx)·ex + x·d(ex)/dx = 1·ex + x·ex = (x+1)·ex
Bedoel je dit?
Jep.. zou je het kunnen simplificeren?quote:
[..]
Hoe bedoel je? In de notatie van Leibniz kun je schrijven
d(x·ex)/dx = (dx/dx)·ex + x·d(ex)/dx = 1·ex + x·ex = (x+1)·ex
Bedoel je dit?
Het was iets met dy/dp en dx/dp. Die laatste 2 vermenigvuldigen leverde dan weer dy/dx op.
Waar je een deel gelijk stelde aan een ander variabele ofzo..?
Heb het met pen en papier geschetst.. Ik ga het eens op Wolfram Alpha proberen.quote:
[..]
Herleiding van uitdrukkingen met wortels: hiervoor bestaan rekenregels, die Van de Craats ook behandelt in hoofdstuk 3 Machten en wortels. De rekenregels voor wortels zijn nauw verwant met de rekenregels voor machten, omdat je elke wortel immers ook kunt schrijven als een macht met een gebroken (niet gehele) exponent. Verder spelen de rekenregels voor het werken met breuken een rol bij het herleiden van uitdrukkingen met wortels. De waarde van een breuk verandert bijvoorbeeld niet als je teller en noemer met hetzelfde getal (ongelijk nul) vermenigvuldigt, of door hetzelfde getal (ongelijk nul) deelt. Je hebt
[..]
Dat is natuurlijk niet waar. Je moet niet elke curve die een beetje op een parabool lijkt een parabool noemen. Dit is geen kwadratische functie maar een vierdemachts polynoomfunctie en de grafiek kan dan ook geen parabool zijn.
[..]
Nee, je kunt toch méér dan één punt hebben in een grafiek met dezelfde laagste functiewaarde?
[..]
Ja, maar wat nu wanneer dat zelfde laagste punt voor twee verschillende waarden van x wordt bereikt? Dan heb je toch twee laagste punten?
[..]
Heb je de grafiek met pen en papier geschetst of door een computerprogramma laten tekenen?
Dat is de kettingregel.quote:
[..]
Jep.. zou je het kunnen simplificeren?
Het was iets met dy/dp en dx/dp. Die laatste 2 vermenigvuldigen leverde dan weer dy/dx op.
Waar je een deel gelijk stelde aan een ander variabele ofzo..?
Nu denk je aan de kettingregel in de notatie van Leibniz, maar voor het differentiëren van een product als xex gebruik je de productregel, en niet de kettingregel.quote:
[..]
Jep.. zou je het kunnen simplificeren?
Het was iets met dy/dp en dp/dx. Die laatste 2 vermenigvuldigen leverde dan weer dy/dx op.
Waar je een deel gelijk stelde aan een ander variabele ofzo..?
Productregel in de notatie van Leibniz:
d(f(x)·g(x))/dx = (d(f(x))/dx)·g(x) + f(x)·(d(g(x))/dx)
Stellen we hier u = f(x) en v = g(x), dan wordt dit:
d(uv)/dx = (du/dx)·v + u·(dv/dx)
Productregel in de notatie van Lagrange:
h(x) = f(x)·g(x) ⇒ h'(x) = f'(x)·g(x) + f(x)·g'(x)
Of, symbolisch en compacter opgeschreven:
(fg)' = f'g + fg'
Kettingregel in de notatie van Leibniz:
d(g(f(x))/dx = d(g(f(x))/d(f(x)) · d(f(x))/dx
Stellen we hier u = f(x) en y = g(u), dan is y = g(f(x)) en hebben we dus
dy/dx = dy/du · du/dx
Kettingregel in de notatie van Lagrange:
h(x) = g(f(x)) ⇒ h'(x) = g'(f(x))·f'(x)
Of, symbolisch en compacter opgeschreven:
(g∘f)' = (g'∘f)·f'
Het rondje ∘ duidt hier compositie aan en wordt uitgesproken als na, zodat je g∘f dus uitspreekt als g na f. Het lijkt wat onnatuurlijk om een samenstelling van twee functies f en g waarbij f eerst komt zo aan te geven omdat ons schrift van links naar rechts loopt, maar het grote voordeel is dat de volgorde van de letters f en g zo hetzelfde is als bij de haakjesnotatie g(f(x)) voor de samenstelling van twee functies f en g.
Zie je nu de verschillen tussen de productregel en de kettingregel en de verschillen en de overeenkomsten tussen de verschillende notaties?
[ Bericht 0% gewijzigd door Riparius op 16-05-2014 10:58:53 ]
Nog meer over notatie: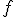 
is een functie, 
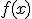is een functie geëvalueerd op het punt 
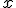, oftewel een getal. Je kan dus nooit spreken over de functie .
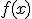Toch gebeurt dat veel, en niet alleen in schoolboeken. Ook Van de Craats heeft het voortdurend over een functie f(x) of over de functie f(x) = x2 als hij een reële functie f van een reële variabele bedoelt resp. een functie f: R → R gedefinieerd door x ↦ x2 oftewel door het functievoorschrift f(x) = x2. Maar het is nogal omslachtig om dat steeds zo op te schrijven en dat verklaart waarom veel auteurs het kortweg hebben over een functie f(x) of de functie f(x) = x2. En dat is ook niet echt bezwaarlijk mits maar duidelijk is - en ook expliciet wordt gemaakt - wat er precies mee wordt bedoeld.quote:
Nog meer over notatie:
Bij een definitie van een functie hoort trouwens ook altijd een specificatie van een domein en een codomein, maar ook dat wordt vaak niet vermeld. De stilzwijgende afspraak bij reële functies van reële variabelen in schoolboeken is dan gewoonlijk dat - tenzij anders vermeld - het domein bestaat uit de grootst mogelijke deelverzameling van R waarvoor het gegeven functievoorschrift betekenis heeft binnen R, en dat R het codomein is.
Aangezien de laatste letters van het alfabet (in ieder geval x, y, z maar vaak ook t, u, v, w) doorgaans variabele of onbekende grootheden aanduiden, kun je de opvatting verdedigen dat de notatie f(x) voor het beeld van x ∈ D bij een functie f: D → R met D ⊂ R ook een variabele grootheid voorstelt, en dus geen vast getal. De letters a, b, c, d maar ook p, q, r, s worden daarentegen gewoonlijk gebruikt om constante of bekende grootheden aan te duiden, en dus kun je dan inderdaad gegeven een reële functie f van een reële variabele de notatie f(a) alleen opvatten als een getal, namelijk de waarde van f(x) voor x = a, oftewel het beeld van a, vooropgesteld dat a ∈ Df. Je ziet dan (terecht) ook nooit dat Van de Craats het heeft over een functie f(a), maar wel dat hij bijvoorbeeld de vergelijking van de raaklijn aan de grafiek van een (differentieerbare) functie f in het punt (a; f(a)) geeft als y = f(a) + f'(a)·(x − a) en hier stellen f(a) en f'(a) uiteraard constante resp. bekende reële grootheden voor.
Maar wat Van de Craats ook doet, en wat is af te keuren, ook in schoolboeken, is dat hij het in opgaven heeft over een functie x2 en dat moet je niet doen, een uitdrukking is iets anders dan een functie.
[ Bericht 0% gewijzigd door Riparius op 16-05-2014 09:32:23 ]
Hier heb je een grafiek van de functie f(x) = x4 − 2x2 (in rood) alsmede van de afgeleide functie f'(x) = 4x3 − 4x (in blauw).quote:
[..]
Bij x^4 - 2x², maar bij de tekening zie ik de globale minima en het lokale maximum niet ... Het is een dalparabool in mijn tekening. Wanneer is er overigens sprake van een globaal minimum en wanneer van een lokaal minimum? Ik dacht dat er alleen maar één globaal minimum in een grafiek mogelijk was (het laagste punt in een grafiek).
[snip]
Met 20.39 a is het probleem de schrijfwijze, zoals eerder gezegd, en bij 20.39 b is het probleem dat de grafiek niet overeenkomt met het antwoord (althans bij mij..). Het antwoord heb ik overigens wel goed.
Je ziet dat de grafiek van f geen parabool is en dat f voor twee verschillende waarden van x een globaal minimum bereikt, en dat de functie ook nog een locaal maximum heeft, maar geen globaal maximum.
Kijk je naar de grafiek van de afgeleide functie f', dan zie dat de afgeleide functie drie nulpunten heeft, namelijk −1, 0 en 1. Bij x = −1 passeert de grafiek van f' de x-as en de steilheid van de grafiek van f' in dit punt oftewel f''(−1) is positief. Ga dit na door de tweede afgeleide te bepalen en f''(−1) te berekenen. Aangezien f'(x) bij x = −1 wisselt van negatief naar positief, gaat de grafiek van f hier over van dalend naar stijgend. Dat betekent dus dat f bij x = −1 in ieder geval een lokaal minimum heeft. De waarde van dit lokale minimum is f(−1) = −1.
Kijken we nu naar het nulpunt x = 0 van de afgeleide functie f', dan zien we dat f'(x) bij x = 0 wisselt van positief naar negatief. De steilheid van de grafiek van f' in dit punt oftewel f''(0) is negatief. Ga dit weer na door f''(0) te berekenen. Aangezien f'(x) bij x = 0 wisselt van positief naar negatief, gaat de grafiek van f hier over van stijgend naar dalend. Dat betekent dus dat f bij x = 0 in ieder geval een lokaal maximum heeft en de waarde van dit lokale maximum is f(0) = 0.
In het nulpunt x = 1 van de afgeleide functie, tenslotte, gaat f'(x) weer over van negatief naar positief en de grafiek van f gaat hier dus weer over van dalend naar stijgend, zodat f bij x = 1 in ieder geval een lokaal minimum heeft met de waarde f(1) = −1.
Uit de grafiek zal je duidelijk zijn dat de twee lokale minima van de functie f bij x = −1 en bij x = 1 tegelijk ook het globale minimum zijn van deze functie. De waarde van dit globale minimum is f(−1) = f(1) = −1. Een functie kan slechts één globaal minimum hebben, maar je ziet dat het prima mogelijk is dat dit globale minimum bij meer dan één waarde van x wordt bereikt. De functie f heeft echter geen globaal maximum, dus f heeft inderdaad alleen een lokaal maximum bij x = 0.
De functie f heeft drie nulpunten, namelijk x = −√2, x = 0 en x = √2. Je ziet hier dus ook dat een functie bij eenzelfde waarde van x, hier x = 0, zowel een nulpunt kan hebben als een extreme waarde kan bereiken.
Wat is het verschil tussen een globale minimum en een lokale minimum en je kunt toch twee globale minimums hebben, mits dezelfde waarde toch? Dus bijv -1 en 1? Maar die - telt dan niet? Want ik zou zeggen dat zowel -1 en 1 verschillen van elkaar als waarde,als je de - meetelt.quote:
[..]
Hier heb je een grafiek van de functie f(x) = x4 − 2x2 (in rood) alsmede van de afgeleide functie f'(x) = 4x3 − 4x (in blauw).
[ afbeelding ]
Je ziet dat de grafiek van f geen parabool is en dat f voor twee verschillende waarden van x een globaal minimum bereikt, en dat de functie ook nog een locaal maximum heeft, maar geen globaal maximum.
Kijk je naar de grafiek van de afgeleide functie f', dan zie dat de afgeleide functie drie nulpunten heeft, namelijk −1, 0 en 1. Bij x = −1 passeert de grafiek van f' de x-as en de steilheid van de grafiek van f' in dit punt oftewel f''(−1) is positief. Ga dit na door de tweede afgeleide te bepalen en f''(−1) te berekenen. Aangezien f'(x) bij x = −1 wisselt van negatief naar positief, gaat de grafiek van f hier over van dalend naar stijgend. Dat betekent dus dat f bij x = −1 in ieder geval een lokaal minimum heeft. De waarde van dit lokale minimum is f(−1) = −1.
Kijken we nu naar het nulpunt x = 0 van de afgeleide functie f', dan zien we dat f'(x) bij x = 0 wisselt van positief naar negatief. De steilheid van de grafiek van f' in dit punt oftewel f''(0) is negatief. Ga dit weer na door f''(0) te berekenen. Aangezien f'(x) bij x = 0 wisselt van positief naar negatief, gaat de grafiek van f hier over van stijgend naar dalend. Dat betekent dus dat f bij x = 0 in ieder geval een lokaal maximum heeft en de waarde van dit lokale maximum is f(0) = 0.
In het nulpunt x = 1 van de afgeleide functie, tenslotte, gaat f'(x) weer over van negatief naar positief en de grafiek van f gaat hier dus weer over van dalend naar stijgend, zodat f bij x = 1 in ieder geval een lokaal minimum heeft met de waarde f(1) = −1.
Uit de grafiek zal je duidelijk zijn dat de twee lokale minima van de functie f bij x = −1 en bij x = 1 tegelijk ook het globale minimum zijn van deze functie. De waarde van dit globale minimum is f(−1) = f(1) = −1. Een functie kan slechts één globaal minimum hebben, maar je ziet dat het prima mogelijk is dat dit globale minimum bij meer dan één waarde van x wordt bereikt. De functie f heeft echter geen globaal maximum, dus f heeft inderdaad alleen een lokaal maximum bij x = 0.
De functie f heeft drie nulpunten, namelijk x = −√2, x = 0 en x = √2. Je ziet hier dus ook dat een functie bij eenzelfde waarde van x, hier x = 0, zowel een nulpunt kan hebben als een extreme waarde kan bereiken.
Is het tenslotte handig om op de toets de grafiek te tekenen? Want ik kan het niet direct zien.. of het een minimum, maximum etc is.
Ja dat is handig. Ten tweede is het meervoud van minimum minima.quote:
[..]
Wat is het verschil tussen een globale minimum en een lokale minimum en je kunt toch twee globale minimums hebben, mits dezelfde waarde toch? Dus bijv -1 en 1? Maar die - telt dan niet? Want ik zou zeggen dat zowel -1 en 1 verschillen van elkaar als waarde,als je de - meetelt.
Is het tenslotte handig om op de toets de grafiek te tekenen? Want ik kan het niet direct zien.. of het een minimum, maximum etc is.
Een globaal minimum is het laagste punt van de functie. -1 < 1, dus is f(x) = 1 geen globaal minimum. Je kunt zeggen dat een functie een lokaal minimum aanneemt als de functie van dalend naar stijgend gaat (dus tekenwisseling van de afgeleide), dit lokale minimum is globaal minimum dan en slechts dan als dit ook het laagste punt is van de functie voor alle waarden waarvoor de functie gedefinieerd is.
Overigens is zijn 1 en -1 alleen in absolute waarde gelijk aan elkaar, dus |1| = 1 = |-1|. -1 en 1 zijn verder geen gelijke waardes.
Fervent tegenstander van het korps lasergamers.
