SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Als je een goede bron voor de CLT zoekt, dan voldoet bijna ieder boek waarbij de woorden "Introduction" en "probability" of "statistics" in de titel voorkomenquote:Op dinsdag 3 december 2013 20:56 schreef Aardappeltaart het volgende:
[..]
Inderdaad interessant, maar als het zo uitgebreid wordt, laat ik het opnemen ervan maar achterwege. Dankjewel! Ik moet al op gaan passen dat het niet té dik gaat worden. Heeft iemand ergens een goeie bron over de CLT? Ik moet er toch naar gaan verwijzen (reden dat metingen van grootheden, gebaseerd op veel variabelen, normaal verdeeld zijn), zonder het zelf helemaal te begrijpen en te bewijzen dan maar. Lijkt me ook interessant om te lezen.
Zojuist mezelf ingeschreven voor Wiskunde aan de UU. Hoera!
Wiskunde aan de UU is een goede keuze


Oh ja, in mijn tekening heb ik in plaats van een o een a gebruikt en ben dit vervolgens vergeten aan te passen.quote:Op dinsdag 3 december 2013 21:24 schreef Riparius het volgende:
Je formule klopt niet, die heb je kennelijk verkeerd overgenomen: daar waar je o hebt staan moet a staan.
Aah, natuurlijk. Ik dacht weer eens te moeilijk.quote:Heel eenvoudig: pas de cosinusregel toe in je scheefhoekige driehoek en gebruik de stelling van Pythagoras voor de hypotenusa van de rechthoekige driehoek, dan heb je
c2 = b2 + (a2 + d2) - 2b·√(a2 + d2)·cos β
Bedankt!


Schrijf de matrix op in elementen en werk uit wat er komt uit de producten Ae1 etc. Dan zie je zo wat de matrix is.quote:Op donderdag 5 december 2013 18:07 schreef Banaanensuiker het volgende:
Kan iemand mij hiermee op weg helpen?
[ afbeelding ]


Ja, dat lukt me wel, maar krijg die t waarde niet uitgerekend op de en of andere manier.quote:Op donderdag 5 december 2013 21:32 schreef thenxero het volgende:
[..]
Schrijf de matrix op in elementen en werk uit wat er komt uit de producten Ae1 etc. Dan zie je zo wat de matrix is.


Je weet dat in het algemeen moet gelden voor eigenwaarden:quote:Op donderdag 5 december 2013 22:20 schreef Banaanensuiker het volgende:
[..]
Ja, dat lukt me wel, maar krijg die t waarde niet uitgerekend op de en of andere manier.
det(A-E*1) = 0 (met 1 de identiteitsmatrix en E de eigenwaarde).
Je weet nu dat 0 een eigenwaarde is.
Wat kun je daar dan uit afleiden?


Ik heb twee datasets zoals hierboven. Nu wil ik op beide een curve fitten waaruit ik een tijdschaal kan halen. Die tijdschaal wil ik dan gaan vergelijken. Een directe exponentiële curve hierop fitten is alleen niet direct mogelijk. Hebben jullie enig advies hoe ik het kan aanpakken?
gr gr


Je hebt voor elk van beide curves iets alsquote:Op vrijdag 6 december 2013 11:29 schreef Quyxz_ het volgende:
[ afbeelding ]
Ik heb twee datasets zoals hierboven. Nu wil ik op beide een curve fitten waaruit ik een tijdschaal kan halen. Die tijdschaal wil ik dan gaan vergelijken. Een directe exponentiële curve hierop fitten is alleen niet direct mogelijk. Hebben jullie enig advies hoe ik het kan aanpakken?
y(t) = a + (b − a)·e−ct
Je zou dan a en b kunnen schatten en vervolgens een best fit voor c en daarmee voor de tijdconstante τ = 1/c kunnen zoeken, maar of dat de beste aanpak is hangt af van de eventuele hulpmiddelen (software) waarover je kunt beschikken, daar zeg je namelijk niets over. Zo te zien naderen beide curves asymptotisch tot ca. 3,25, dus dan heb je voor je beide curves a ≈ 3,25. Voor de blauwe curve is dan verder b ≈ 0,5 en voor de rode b ≈ 5,5.


Zij 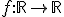 continu, f(0) = 1 en
continu, f(0) = 1 en 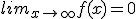 en
en 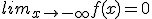
Laat zien:
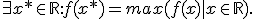
Ik heb werkelijk waar geen idee hoe ik hieraan moet beginnen. Ik denk dat ik moet laten zien dat f(x) sowieso begrensd is naar boven, maar ik heb zo 1,2,3 geen idee hoe ik hieraan moet beginnen. Tipje, iemand?
Laat zien:
Ik heb werkelijk waar geen idee hoe ik hieraan moet beginnen. Ik denk dat ik moet laten zien dat f(x) sowieso begrensd is naar boven, maar ik heb zo 1,2,3 geen idee hoe ik hieraan moet beginnen. Tipje, iemand?


Eerste hint dan maar: wat kun je vertellen over een reële functie die continu is op een gesloten interval?quote:Op zondag 8 december 2013 15:45 schreef Amoeba het volgende:
Zijcontinu, f(0) = 1 en
en
Laat zien:
Ik heb werkelijk waar geen idee hoe ik hieraan moet beginnen. Ik denk dat ik moet laten zien dat f(x) sowieso begrensd is naar boven, maar ik heb zo 1,2,3 geen idee hoe ik hieraan moet beginnen. Tipje, iemand?


Deze bereikt een maximale en een minimale waarde. Dat zal wel het hele idee van die opgave zijn.quote:Op zondag 8 december 2013 21:14 schreef Riparius het volgende:
[..]
Eerste hint dan maar: wat kun je vertellen over een reële functie die continu is op een gesloten interval?
Ik moet ook in termen van rijen denken, wellicht mis ik hier iets. Ik wil inderdaad de stelling van een maximum/minimum gebruiken op een gesloten interval voor een reële, continu functie.
[ Bericht 1% gewijzigd door #ANONIEM op 08-12-2013 21:27:21 ]


Rijen lijken me niet nodig. Hint: Op een gegeven moment is de functie buiten het gesloten interval bevat in [-epsilon, +epsilon]. Leuke opgave, ik kende deze nog niet.quote:Op zondag 8 december 2013 21:26 schreef Amoeba het volgende:
[..]
Deze bereikt een maximale en een minimale waarde. Dat zal wel het hele idee van die opgave zijn.
Ik moet ook in termen van rijen denken, wellicht mis ik hier iets. Ik wil inderdaad de stelling van een maximum/minimum gebruiken op een gesloten interval voor een reële, continu functie.


Aaaah, ik zie het. Doordat f(0) = 1 > 0 kan ik 2 limietdefinities uitschrijven en zo een gesloten interval maken.quote:Op zondag 8 december 2013 23:32 schreef thenxero het volgende:
[..]
Rijen lijken me niet nodig. Hint: Op een gegeven moment is de functie buiten het gesloten interval bevat in [-epsilon, +epsilon]. Leuke opgave, ik kende deze nog niet.


Het rigoreus opschrijven vergt nog wel wat inspanningquote:Op maandag 9 december 2013 00:13 schreef Amoeba het volgende:
[..]
Aaaah, ik zie het. Doordat f(0) = 1 > 0 kan ik 2 limietdefinities uitschrijven en zo een gesloten interval maken.


Ja, maar ik begrijp het idee. Doordat die limiet bestaat is er dus een x* en een x" zodat |f(x)| < 1 voor alle x kleiner gelijk x* en voor alle x groter gelijk x", en dus omdat f(0) = 1 > 0 kan ik dus het gesloten interval [x*, x"] beschouwen en hierop de extremumstelling van Weierstrass toepassen, omdat alles buiten dit interval toch kleiner is dan f(0) = 1.quote:Op maandag 9 december 2013 00:43 schreef thenxero het volgende:
[..]
Het rigoreus opschrijven vergt nog wel wat inspanning.
Ik denk dat ik ook moet vermelden dat 0 een element uit dat interval is, maar in principe spreekt dat voor zich.
[ Bericht 1% gewijzigd door #ANONIEM op 09-12-2013 07:39:30 ]


Bedankt! Qua software heb ik MATLAB tot mijn beschikking met veel toolboxes. Had het al geprobeerd met de Curve Fitting toolbox, maar die werkte niet mee. Zal zo eens kijken naar jouw handmatige methode. Of heeft MATLAB daar ook een geschikte functie voor?quote:Op vrijdag 6 december 2013 17:27 schreef Riparius het volgende:
[..]
Je hebt voor elk van beide curves iets als
y(t) = a + (b − a)·e−ct
Je zou dan a en b kunnen schatten en vervolgens een best fit voor c en daarmee voor de tijdconstante τ = 1/c kunnen zoeken, maar of dat de beste aanpak is hangt af van de eventuele hulpmiddelen (software) waarover je kunt beschikken, daar zeg je namelijk niets over. Zo te zien naderen beide curves asymptotisch tot ca. 3,25, dus dan heb je voor je beide curves a ≈ 3,25. Voor de blauwe curve is dan verder b ≈ 0,5 en voor de rode b ≈ 5,5.
gr gr


Handmatig is helemaal niet zo moeilijk. Ik had al geschatte waarden voor a en b gegeven. Uitquote:Op maandag 9 december 2013 09:18 schreef Quyxz_ het volgende:
[..]
Bedankt! Qua software heb ik MATLAB tot mijn beschikking met veel toolboxes. Had het al geprobeerd met de Curve Fitting toolbox, maar die werkte niet mee. Zal zo eens kijken naar jouw handmatige methode. Of heeft MATLAB daar ook een geschikte functie voor?
volgt
Voor de blauwe curve nemen we a = 3,25, b = 0,5 en lezen we uit de grafiek af dat y(150) = 2, en dat geeft dus c = (1/150)·ln(−2,75/−1,25) ≈ 0,00526 en daarmee τ ≈ 190 sec.
Voor de rode curve nemen we a = 3,25, b = 5,5 en lezen we uit de grafiek af dat y(200) = 4, en dat geeft dus c = (1/200)·ln(2,25/0,75) ≈ 0,00549 en daarmee τ ≈ 182 sec.
De (geschatte) tijdconstantes liggen dicht bij elkaar, en dat is ook niet zo vreemd, want de curves zijn vrijwel elkaars spiegelbeeld in hun gemeenschappelijke horizontale asymptoot.
Als je de meetwaarden in numerieke vorm hebt, dan kun je uiteraard een betere fit krijgen dan je alleen uit de grafiek kunt afleiden. Wil je dat doen met Matlab, kijk dan eens hier.


Heel goedquote:Op maandag 9 december 2013 07:37 schreef Amoeba het volgende:
[..]
Ja, maar ik begrijp het idee. Doordat die limiet bestaat is er dus een x* en een x" zodat |f(x)| < 1 voor alle x kleiner gelijk x* en voor alle x groter gelijk x", en dus omdat f(0) = 1 > 0 kan ik dus het gesloten interval [x*, x"] beschouwen en hierop de extremumstelling van Weierstrass toepassen, omdat alles buiten dit interval toch kleiner is dan f(0) = 1.
Ik denk dat ik ook moet vermelden dat 0 een element uit dat interval is, maar in principe spreekt dat voor zich.


Nogmaals bedankt!quote:Op maandag 9 december 2013 10:14 schreef Riparius het volgende:
[..]
Handmatig is helemaal niet zo moeilijk. Ik had al geschatte waarden voor a en b gegeven. Uit
volgt
Voor de blauwe curve nemen we a = 3,25, b = 0,5 en lezen we uit de grafiek af dat y(150) = 2, en dat geeft dus c = (1/150)·ln(−2,75/−1,25) ≈ 0,00526 en daarmee τ ≈ 190 sec.
Voor de rode curve nemen we a = 3,25, b = 5,5 en lezen we uit de grafiek af dat y(200) = 4, en dat geeft dus c = (1/200)·ln(2,25/0,75) ≈ 0,00549 en daarmee τ ≈ 182 sec.
De (geschatte) tijdconstantes liggen dicht bij elkaar, en dat is ook niet zo vreemd, want de curves zijn vrijwel elkaars spiegelbeeld in hun gemeenschappelijke horizontale asymptoot.
Als je de meetwaarden in numerieke vorm hebt, dan kun je uiteraard een betere fit krijgen dan je alleen uit de grafiek kunt afleiden. Wil je dat doen met Matlab, kijk dan eens hier.
Code voor de vorm: (met x en y de ingangsdata)
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | for a=3:0.0005:3.5; for b=0:000.1:1; k=k+1; situation(k,:)=[a b]; c=(1./x).*log((b-a)./(y-a)); tau=c.^-1; taustd(k)=std(tau); end end idealk=find(taustd==min(taustd)) |
Het doel is overigens om te controleren of de tijdsconstantes gelijkwaardig zijn, dus vandaar!
gr gr


Ik ben aan het klunzen met een vraagstuk dat niet zo moeilijk moet zijn.
Mij word gevraagd om het volgende te differentieren: http://www.wolframalpha.com/input/?i=%28sinx%29^6+%2B+%28cosx%29^6
Ik verdeel de functie in twee functies g(x) en h(x).
g'(x)=6(sinx)^5 * cosx
h'(x)= - 6(cosx)^5 * sinx
Samenvoegen geeft
6sin(x)^5 * cosx - 6(cosx)^5 * sinx
Delen door 6 geeft
sin(x)^5 * cosx - cos(x)^5 * sin x Ik zou hier een goniometrische identiteit op los kunnen laten, maar waarom zou ik.
Delen door eerst cos x en daarna sin x geeft
sin(x)^4 - cos(x)^4
Dit klopt echter niet....Of ik schrijf het op een andere manier. Ik zie werkelijk niet waar ik de mist in ga. Telkens gebruik ik goede algebra.
Mij word gevraagd om het volgende te differentieren: http://www.wolframalpha.com/input/?i=%28sinx%29^6+%2B+%28cosx%29^6
Ik verdeel de functie in twee functies g(x) en h(x).
g'(x)=6(sinx)^5 * cosx
h'(x)= - 6(cosx)^5 * sinx
Samenvoegen geeft
6sin(x)^5 * cosx - 6(cosx)^5 * sinx
Delen door 6 geeft
sin(x)^5 * cosx - cos(x)^5 * sin x Ik zou hier een goniometrische identiteit op los kunnen laten, maar waarom zou ik.
Delen door eerst cos x en daarna sin x geeft
sin(x)^4 - cos(x)^4
Dit klopt echter niet....Of ik schrijf het op een andere manier. Ik zie werkelijk niet waar ik de mist in ga. Telkens gebruik ik goede algebra.


Je mag toch niet gewoon een term wegdelen?quote:Op maandag 9 december 2013 23:14 schreef DefinitionX het volgende:
Ik ben aan het klunzen met een vraagstuk dat niet zo moeilijk moet zijn.
Mij word gevraagd om het volgende te differentieren: http://www.wolframalpha.com/input/?i=%28sinx%29^6+%2B+%28cosx%29^6
Ik verdeel de functie in twee functies g(x) en h(x).
g'(x)=6(sinx)^5 * cosx
h'(x)= - 6(cosx)^5 * sinx
Samenvoegen geeft
6sin(x)^5 * cosx - 6(cosx)^5 * sinx
Delen door 6 geeft
sin(x)^5 * cosx - cos(x)^5 * sin x Ik zou hier een goniometrische identiteit op los kunnen laten, maar waarom zou ik.
Delen door eerst cos x en daarna sin x geeft
sin(x)^4 - cos(x)^4
Dit klopt echter niet....Of ik schrijf het op een andere manier. Ik zie werkelijk niet waar ik de mist in ga. Telkens gebruik ik goede algebra.
Als je functie x^3 is, dan is je afgeleide 3*x^2. Je mag dan niet opeens een x wegstrepen, want dan heb je 3*x en dat is een heel andere functie. Je mag natuurlijk wel een x buiten de haakjes halen, zodat je x*(3x) krijgt, dat is gewoon dezelfde functie. Zo mag jij in je opgave wel gewoon 6cos(x)sin(x) buiten haakjes halen, maar deze mag je niet zomaar wegstrepen.


Ik weet het nu even niet meer. Als ik in stappen terug ga:
sin(x)^4 - cos(x)^4
vermenigvuldigen met sin(x) geeft
sin(x)^5 - cos(x)^4sin(x)
vermenigvuldigen met cos(x) geeft
sin(x)^5cos(x) - cos(x)^5sin(x)
vermenigvuldigen met 6 geeft
6sin(x)^5 * cosx - 6(cosx)^5 * sinx
Ik dacht dat ik aan het vereenvoudigen was.
Edit:
Alrac4, ik denk dat je gelijk hebt. Morgen maar even terugkijken naar deze vraagstuk, of zometeen.
sin(x)^4 - cos(x)^4
vermenigvuldigen met sin(x) geeft
sin(x)^5 - cos(x)^4sin(x)
vermenigvuldigen met cos(x) geeft
sin(x)^5cos(x) - cos(x)^5sin(x)
vermenigvuldigen met 6 geeft
6sin(x)^5 * cosx - 6(cosx)^5 * sinx
Ik dacht dat ik aan het vereenvoudigen was.
Edit:
Alrac4, ik denk dat je gelijk hebt. Morgen maar even terugkijken naar deze vraagstuk, of zometeen.


6sin5(x) - 6cos5(x) =
6sin(x)cos(x)(sin4(x) - cos4(x)) =
6sin(x)cos(x)(sin2(x) - cos2(x))(sin2(x) + cos2(x)) =
3sin(2x) * - cos(2x) * 1 =
-1½ * sin(4x)
6sin(x)cos(x)(sin4(x) - cos4(x)) =
6sin(x)cos(x)(sin2(x) - cos2(x))(sin2(x) + cos2(x)) =
3sin(2x) * - cos(2x) * 1 =
-1½ * sin(4x)


Differentiëren en vervolgens vereenvoudigen van het resultaat zijn twee heel verschillende bewerkingen ...quote:Op maandag 9 december 2013 23:59 schreef DefinitionX het volgende:
Ik weet het nu even niet meer.
Ik dacht dat ik aan het vereenvoudigen was.
Je functie was
en differentiëren hiervan (met behulp van de kettingregel) geeft inderdaad
Nu kun je een factor 6·sin x·cos x buiten haakjes halen, en dat geeft
De factor tussen haakjes kunnen we nu ontbinden met behulp van het merkwaardig product a2 − b2 = (a − b)(a + b), zodat we krijgen
Maar nu weten we dat sin 2α = 2·sin α·cos α en cos 2α = cos2α − sin2α en ook is sin2x + cos2x = 1, zodat we dus krijgen
Nu zie je dat we nogmaals gebruik kunnen maken van de identiteit sin 2α = 2·sin α·cos α voor de sinus van de dubbele hoek, zodat we uiteindelijk krijgen
[ Bericht 1% gewijzigd door Riparius op 11-12-2013 10:43:53 ]


Voor mijn studie wiskunde ben ik op zoek naar enkele extra dicaten over matrices. Met name met uitleg over basisbewerkingen en lekker veel opdrachten  Kan iemand mij helpen? Boek van vd craats heb ik al.
Kan iemand mij helpen? Boek van vd craats heb ik al.


Als iemand even tijd heeft......Hoe zouden jullie de primitieve functie van deze functie vinden:
f(x) = 1/ (1 + x^2)
Ik zou graag de tussenstappen ook willen zien.
f(x) = 1/ (1 + x^2)
Ik zou graag de tussenstappen ook willen zien.


Dit is een standaardprimitieve. Het blijkt dat de afgeleide van arctan(x) gelijk is aan f(x), dus als je de stappen van de afgeleide kunt volgen van F(x) (hint: denk aan de formele definitie van de afgeleide) dan weet je de primitieve functie.quote:Op dinsdag 10 december 2013 16:49 schreef DefinitionX het volgende:
Als iemand even tijd heeft......Hoe zouden jullie de primitieve functie van deze functie vinden:
f(x) = 1/ (1 + x^2)
Ik zou graag de tussenstappen ook willen zien.
[ Bericht 0% gewijzigd door #ANONIEM op 10-12-2013 16:59:21 ]


Ik heb een vraagje over analyse. Zij f: R -> R, f continu op R met periode T > 0
Laat zien: er is een x zodanig dat f(x) = f(x+T/2)
Ik weet dat f(x) = f(x+T) omdat f periodiek is met periode T, maar hoe ik dan aantoon dat er zo'n waarde bestaat weet ik niet.
Wederom vraag ik niet om een uitwerking, maar om een duwtje in de goede richting. Ik kom steeds uit op de tussenwaardestelling, mjah, hoe gebruik ik die?
Ik zat te denken aan een bewijs uit het ongerijmde. Stel er is géén x zodanig dat f(x) = f(x+T/2), dan is f(x) - f(x+T/2) ongelijk 0 voor alle x, maar kan ik nu al een tussenwaardestelling toepassen om te laten zien dat dit niet waar is?
Wacht wacht ik denk dat ik hem heb! Werk hem zo even uit.
[ Bericht 4% gewijzigd door #ANONIEM op 10-12-2013 18:04:51 ]
Laat zien: er is een x zodanig dat f(x) = f(x+T/2)
Ik weet dat f(x) = f(x+T) omdat f periodiek is met periode T, maar hoe ik dan aantoon dat er zo'n waarde bestaat weet ik niet.
Wederom vraag ik niet om een uitwerking, maar om een duwtje in de goede richting. Ik kom steeds uit op de tussenwaardestelling, mjah, hoe gebruik ik die?
Ik zat te denken aan een bewijs uit het ongerijmde. Stel er is géén x zodanig dat f(x) = f(x+T/2), dan is f(x) - f(x+T/2) ongelijk 0 voor alle x, maar kan ik nu al een tussenwaardestelling toepassen om te laten zien dat dit niet waar is?
Wacht wacht ik denk dat ik hem heb! Werk hem zo even uit.
[ Bericht 4% gewijzigd door #ANONIEM op 10-12-2013 18:04:51 ]


Bij een xy-plot kan je een (of meerdere) curve(s) trekken waarbij x*y gelijk is aan een (verschillende) constante(s), is er een naam voor die lijn(en)?
Voegt hoogtepunten toe aan jullie druilerige bestaan.


Hyperbool, zoek je dat?quote:Op dinsdag 10 december 2013 17:15 schreef 2thmx het volgende:
Bij een xy-plot kan je een (of meerdere) curve(s) trekken waarbij x*y gelijk is aan een (verschillende) constante(s), is er een naam voor die lijn(en)?


quote:Op dinsdag 10 december 2013 17:06 schreef Amoeba het volgende:
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Willen jullie even verifiëren of mijn bewijs juist is?
Bewijs:
Definieer: f: R → R continu en periodiek met T>0
Definieer: g(x) = f(x) - f(x+T/2), g(x) is een verschil van 2 continu periodieke functies en is dus zelf ook periodiek en continu.
Neem aan dat er géén waarde x ∈ R bestaat zodanig dat f(x) = f(x+T/2)
dan:
(1): ∃x ∈ R: f(x) > f(x+T/2) (of andersom: analoog)
Neem nu aan dat f(x) > f(x+T/2) ∀x ∈ R
Dit kan niet, want als f(x) > f(x+T/2) ∀x ∈ R, dan f(x) > f(x+T/2) > f(x+T), en er geldt juist f(x) = f(x+T), dus: (?)
(2):: ∃x ∈ R: f(x) < f(x+T/2)
dus:
(1) ∃x1 ∈ R: ⇒ g(x) > 0
(2) ∃x2 ∈ R: ⇒ g(x) < 0
Passen we nu de tussenwaardestelling op g(x) toe dan:
∃x3 ∈ [x1, x2]: g(x3) = 0 ⇒ f(x3) - f(x3+T/2) = 0 ⇒ f(x3) = f(x3+T/2) en het gevraagde volgt.
Ik heb ergens een (?) bij geplaatst. Dit formuleren vind ik nogal lastig, wellicht maak ik hier een fout. Kan iemand me dan vertellen hoe ik dat wel goed opschrijf?
[ Bericht 0% gewijzigd door #ANONIEM op 10-12-2013 19:06:22 ]


Substitueer x=tan(x)quote:Op dinsdag 10 december 2013 16:49 schreef DefinitionX het volgende:
Als iemand even tijd heeft......Hoe zouden jullie de primitieve functie van deze functie vinden:
f(x) = 1/ (1 + x^2)
Ik zou graag de tussenstappen ook willen zien.


Ik neem aan dat je met (1) en (2) bedoelt geval 1 en geval 2. Wel raar dat je binnen geval (1) je aanname opeens verruimt naar "voor alle x" ipv "er bestaat een x".quote:Op dinsdag 10 december 2013 18:48 schreef Amoeba het volgende:
[..]
[ afbeelding ]
Willen jullie even verifiëren of mijn bewijs juist is?
Bewijs:
Definieer: f: R → R continu en periodiek met T>0
Definieer: g(x) = f(x) - f(x+T/2), g(x) is een verschil van 2 continu periodieke functies en is dus zelf ook periodiek en continu.
Neem aan dat er géén waarde x ∈ R bestaat zodanig dat f(x) = f(x+T/2)
dan:
(1): ∃x ∈ R: f(x) > f(x+T/2) (of andersom: analoog)
Neem nu aan dat f(x) > f(x+T/2) ∀x ∈ R
Dit kan niet, want als f(x) > f(x+T/2) ∀x ∈ R, dan f(x) > f(x+T/2) > f(x+T), en er geldt juist f(x) = f(x+T), dus: (?)
(2):: ∃x ∈ R: f(x) < f(x+T/2)
dus:
(1) ∃x1 ∈ R: ⇒ g(x) > 0
(2) ∃x2 ∈ R: ⇒ g(x) < 0
Passen we nu de tussenwaardestelling op g(x) toe dan:
∃x3 ∈ [x1, x2]: g(x3) = 0 ⇒ f(x3) - f(x3+T/2) = 0 ⇒ f(x3) = f(x3+T/2) en het gevraagde volgt.
Ik heb ergens een (?) bij geplaatst. Dit formuleren vind ik nogal lastig, wellicht maak ik hier een fout. Kan iemand me dan vertellen hoe ik dat wel goed opschrijf?
Dus nogal vaag opgeschreven, maar er zitten wel juiste ideeën in.


Dit mag natuurlijk nooit. x = tan(x) is een relatie waarbij x = tan(x) voor alle x in het domein. En dat is niet het geval voor R...quote:
[ Bericht 6% gewijzigd door #ANONIEM op 10-12-2013 20:34:01 ]


Betere notatie is inderdaad x=tan(y) ofquote:Op dinsdag 10 december 2013 20:27 schreef Amoeba het volgende:
[..]
Dit mag natuurlijk nooit. x = tan(x) is een relatie waarbij x = tan(x) voor alle x in het domein. Nou, dan beperk je je domein tot 0, en dat is natuurlijk niet wenselijk.
Maar het punt van de poster lijkt me duidelijk


Jazeker. Ik neem aan dat f(x) > f(x+T/2) voor alle x, en wil laten zien dat dit niet kan, zodat er een x bestaat waarvoor f(x) < f(x+T/2). Maar hoe laat ik dat netjes zien?quote:Op dinsdag 10 december 2013 20:27 schreef thenxero het volgende:
[..]
Ik neem aan dat je met (1) en (2) bedoelt geval 1 en geval 2. Wel raar dat je binnen geval (1) je aanname opeens verruimt naar "voor alle x" ipv "er bestaat een x".
Dus nogal vaag opgeschreven, maar er zitten wel juiste ideeën in.
Inderdaad. Dan krijg je inderdaad een uitdrukking die je wel kunt integreren. Wilde even dat hij het zelf zou zien.quote:Op dinsdag 10 december 2013 20:28 schreef thenxero het volgende:
[..]
Betere notatie is inderdaad x=tan(y) of
Maar het punt van de poster lijkt me duidelijk.
[ Bericht 36% gewijzigd door #ANONIEM op 10-12-2013 20:31:35 ]


Dat heb je toch ook gedaan (alleen dan dat f(x) <= f(x+T/2)) ?quote:Op dinsdag 10 december 2013 20:29 schreef Amoeba het volgende:
[..]
Jazeker. Ik neem aan dat f(x) > f(x+T/2) voor alle x, en wil laten zien dat dit niet kan, zodat er een x bestaat waarvoor f(x) < f(x+T/2). Maar hoe laat ik dat netjes zien?
Je laat zien "niet voor alle x geldt f(x) > f(x+T/2)" en dus "er bestaat een x zodat f(x) <= f(x+T/2)".


Ja dat komt op hetzelfde neer. Mijn vraag is of die redenering juist is. Onze instructeur kijkt nogal streng na, en dit is een inleveropgave voor het van Analyse I. Vandaar dat ik het even goed op wil schrijven. En jazeker, ik heb dit helemaal zelf verzonnen. Ik moest denken aan die post waar ik ook zo'n probleem met de tussenwaardestelling had.quote:Op dinsdag 10 december 2013 20:32 schreef thenxero het volgende:
[..]
Dat heb je toch ook gedaan (alleen dan dat f(x) <= f(x+T/2)) ?
Je laat zien "niet voor alle x geldt f(x) > f(x+T/2)" en dus "er bestaat een x zodat f(x) <= f(x+T/2)".


Dat stukje van de redenering is goed. Maar de bewijsstructuur is niet goed of op zijn minst rommelig. Kijk daar nog eens naar.quote:Op dinsdag 10 december 2013 20:36 schreef Amoeba het volgende:
[..]
Ja dat komt op hetzelfde neer. Mijn vraag is of die redenering juist is. Onze instructeur kijkt nogal streng na, en dit is een inleveropgave voor het van Analyse I. Vandaar dat ik het even goed op wil schrijven. En jazeker, ik heb dit helemaal zelf verzonnen. Ik moest denken aan die post waar ik ook zo'n probleem met de tussenwaardestelling had.
En is een verschil van periodieke functies wel altijd periodiek? Neem een functie met periode 1 en één met periode pi. Wat is de periode van het verschil?


Je maakt het veel te moeilijk. Je kunt gemakkelijk laten zien dat voor jouw functie g(x) geldtquote:Op dinsdag 10 december 2013 20:36 schreef Amoeba het volgende:
[..]
Ja dat komt op hetzelfde neer. Mijn vraag is of die redenering juist is. Onze instructeur kijkt nogal streng na, en dit is een inleveropgave voor het van Analyse I. Vandaar dat ik het even goed op wil schrijven. En jazeker, ik heb dit helemaal zelf verzonnen. Ik moest denken aan die post waar ik ook zo'n probleem met de tussenwaardestelling had.
g(T/2) = −g(0)
Als g(0) = 0 dan is er niets meer te bewijzen, dus veronderstel g(0) ≠ 0. Dan hebben g(0) en g(T/2) een tegengesteld teken, en is er dus volgens de tussenwaardestelling een ξ ∈ (0, T/2) zodanig dat g(ξ) = 0 en daarmee f(ξ) = f(ξ + T/2), QED.


Het maakt eigenlijk ook geen fluit of g(x) periodiek is. Doet niet eens ter zake.quote:Op dinsdag 10 december 2013 21:05 schreef thenxero het volgende:
[..]
Dat stukje van de redenering is goed. Maar de bewijsstructuur is niet goed of op zijn minst rommelig. Kijk daar nog eens naar.
En is een verschil van periodieke functies wel altijd periodiek? Neem een functie met periode 1 en één met periode pi. Wat is de periode van het verschil?
Crap, je bent echt een genie.quote:Op dinsdag 10 december 2013 21:18 schreef Riparius het volgende:
[..]
Je maakt het veel te moeilijk. Je kunt gemakkelijk laten zien dat voor jouw functie g(x) geldt
g(T/2) = −g(0)
Als g(0) = 0 dan is er niets meer te bewijzen, dus veronderstel g(0) ≠ 0. Dan hebben g(0) en g(T/2) een tegengesteld teken, en is er dus volgens de tussenwaardestelling een ξ ∈ (0, T/2) zodanig dat g(ξ) = 0 en daarmee f(ξ) = f(ξ + T/2), QED.
[ Bericht 4% gewijzigd door #ANONIEM op 10-12-2013 22:03:47 ]


En opmerking vooraf: je kunt niet spreken van de primitieve van een functie, omdat een primitieve altijd slechts tot op een constante is bepaald: als F(x) een primitieve is van f(x), dan is G(x) = F(x) + C met een willekeurige constante C eveneens een primitieve van f(x), omdat de afgeleide van een constante immers nul is en je dus ook hebt G'(x) = F'(x) + 0 = f(x).quote:Op dinsdag 10 december 2013 16:49 schreef DefinitionX het volgende:
Als iemand even tijd heeft......Hoe zouden jullie de primitieve functie van deze functie vinden:
f(x) = 1/ (1 + x^2)
Ik zou graag de tussenstappen ook willen zien.
Je hebt
Dit is een standaardintegraal, een primitieve van f(x) = 1/(1 + x2) is F(x) = arctan x oftewel de inverse van de tangens functie. Let op dat men de inversen van de goniometrische functies in Vlaanderen meestal noteert met het prefix bg voor 'boog' en dus niet met het prefix arc voor 'arcus' (Latijn voor 'boog').
Om te begrijpen hoe dit zit moet je eerst weten wat de afgeleide is van de tangens functie en hoe het verband is tussen de afgeleiden van twee functies die elkaars inverse zijn. Als je hebt
g(x) = tan x
dan is
g'(x) = 1 + tan2x
Ga dit na door te schrijven g(x) = sin x / cos x, en dan gebruik te maken van de quotiëntregel om g'(x) te bepalen. De afgeleide van de tangens functie is ook nog op een andere manier te schrijven, namelijk
g'(x) = 1 / cos2x
en aangezien de secans de multplicatieve inverse is van de cosinus, zou je hiervoor ook nog kunnen schrijven
g'(x) = sec2x
maar dit laatste wordt nog maar zelden gedaan.
Heb je twee functies f en g dan kun je ook een samengestelde functie h maken, waarbij je als het ware de 'output' van de eerste functie f weer gebruikt als 'input' voor de tweede functie g, zodat je dus hebt
h(x) = g(f(x))
Zoals bekend vertelt de kettingregel je dan hoe je de afgeleide kunt bepalen van deze samengestelde functie, als je tenminste al weet hoe je de afgeleiden van f en g bepaalt:
h'(x) = g'(f(x))·f'(x)
Maar stel nu eens dat f en g elkaars inverse zijn. Dan doet g weer teniet wat f heeft bewerkstelligd, dus als we de 'output' van f in g stoppen als 'input', dan geeft g weer de oorspronkelijke 'input' x van f terug, dus
g(f(x)) = x
Maar dan is dus h(x) = g(f(x)) = x, zodat h'(x) = 1 moet zijn. Maar we weten dat volgens de kettingregel h'(x) = g'(f(x))·f'(x), en dus hebben we nu
g'(f(x))·f'(x) = 1
zodat
f'(x) = 1 / g'(f(x))
Welnu, stel dat f(x) = arctan x en g(x) = tan x, dan weten we al dat
g'(x) = 1 + tan2x = 1 + (g(x))2
zodat
g'(f(x)) = 1 + (g(f(x)))2 = 1 + x2
en dus hebben we
f'(x) = 1 / g'(f(x)) = 1/(1 + x2)
De afgeleide van f(x) = arctan x is dus inderdaad f'(x) = 1/(1 + x2), zodat arctan x een primitieve is van 1/(1 + x2).
Waar je wel op moet letten bij periodieke functies, zoals de goniometrische functies, is dat je hier niet 'zomaar' kunt spreken van een inverse functie. Immers, arctan x = θ impliceert tan θ = x, maar je mag dit niet omkeren. Uit tan θ = x volgt niet zonder meer dat arctan x = θ, omdat er voor elke reële waarde van x oneindig veel waarden van θ zijn waarvoor tan θ = x, de tangens functie is immers een periodieke functie met een periode π. Men moest dus een keuze maken en bij elke reële x één van de waarden van θ kiezen waarvoor tan θ = x. De afspraak is dat men dan de waarde van θ (uitgedrukt in radialen) op het interval (−π/2, π/2) kiest. Met arctan x bedoelen we dus de (unieke) waarde van θ (in radialen) op het interval (−π/2, π/2) waarvoor tan θ = x. Zo heb je bijvoorbeeld arctan(1) = π/4 omdat tan(π/4) = 1 en omdat π/4 de enige waarde is op het interval (−π/2, π/2) waarvan de tangens gelijk is aan 1.
[ Bericht 0% gewijzigd door Riparius op 12-12-2013 02:23:57 ]


Exponentiële functie?quote:Op dinsdag 10 december 2013 23:48 schreef 2thmx het volgende:
[..]
Nee, ik bedoel een naam voor specifiek de curve die ik omschrijf. Zoiets: [ afbeelding ]
Kan goed zijn dat er geen naam voor bestaat hoor.


Nee, ik bedoel dus een naam specifiek voor deze curvequote:
Voegt hoogtepunten toe aan jullie druilerige bestaan.


De curve in je figuur is één tak van een orthogonale hyperbool. De andere tak ligt in het derde kwadrant. Deze hyperbool heet orthogonaal omdat de asymptoten van deze hyperbool loodrecht op elkaar staan, de coördinaatassen zijn immers de asymptoten.quote:Op dinsdag 10 december 2013 23:52 schreef 2thmx het volgende:
[..]
Nee, ik bedoel dus een naam specifiek voor deze curve. Als die bestaat, that is.


Ah dat kan niet. Er is geen veelvoud van 1 wat deelbaar is door piquote:Op dinsdag 10 december 2013 21:05 schreef thenxero het volgende:
[..]
Dat stukje van de redenering is goed. Maar de bewijsstructuur is niet goed of op zijn minst rommelig. Kijk daar nog eens naar.
En is een verschil van periodieke functies wel altijd periodiek? Neem een functie met periode 1 en één met periode pi. Wat is de periode van het verschil?
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |





