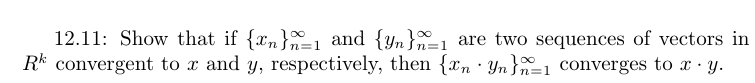[Bèta wiskunde] Huiswerk- en vragentopic

m'n notatie klopt want wolfram pakt em meteen, weet niet hoe je de juiste leesbare notatie moet gebruiken hier.
maar die site is idd handig, thanks

ik zie m'n fout lol, stom

Hoe kan je dit het beste aanpakken? In R¹ lukken me dit soort bewijzen wel, maar in R^k heb ik er meer moeite mee. Ik neem aan dat we de euclidean norm ergens moet gebruiken en een shitload een triangle inequalities?

EDIT:
Iemand die een fout kan spotten? Ik denk eigenlijk dat het definiëren van c(n) overbodig is, maar ach...

[ Bericht 13% gewijzigd door Novermars op 20-11-2013 23:41:11 ]

Stel je hebt een functie f met f(y,y') (dus onafhankelijk van x). Als je dan de niet-partiele afgeleide df/dx neemt, wat doe je dan precies?

quote:

Op woensdag 20 november 2013 22:01 schreef Crisisstudent het volgende:
Stel je hebt een functie f met f(y,y') (dus onafhankelijk van x). Als je dan de niet-partiele afgeleide df/dx neemt, wat doe je dan precies?

Hoe kun je differentiëren naar x als f onafhankelijk is van x?

quote:

Op woensdag 20 november 2013 21:49 schreef Novermars het volgende:
[ afbeelding ]
Hoe kan je dit het beste aanpakken? In R¹ lukken me dit soort bewijzen wel, maar in R^k heb ik er meer moeite mee. Ik neem aan dat we de euclidean norm ergens moet gebruiken en een shitload een triangle inequalities?

EDIT: [ afbeelding ]
Iemand die een fout kan spotten?

Je bewijs klopt niet. Je beweert o.m. dat |β| < |β+1| maar dat is in zijn algemeenheid niet juist (neem β = −¾).

Houd de notatie aan van het oorspronkelijke vraagstuk en gebruik dat

x_n·y_n − x·y = x_n·(y_n − y) + y·(x_n − x)

en dus

|x_n·y_n − x·y| ≤ ||x_n||·||y_n − y|| + ||y||·||x_n − x||

De notatie die ik nu heb, dus met alpha en beta etc is de notatie die de hooglerares gebruikt, de x en y notatie gebruikt het boek. (dit was een opgave uit het boek). Aangezien de hooglerares mijn tentamens nakijkt, prefereer ik de eerste notatie.

Maar inhoudelijk, mee eens dat het niet klopt. Is het eventueel snel te fixen door vanaf de ongelijkheid, r5 van onder, absolute waardes te gebruiken en van de 1 die ik er bij optel om problemen te voorkomen als beta =0 is een epsilon te maken? Of kan ik beter gewoon opnieuw beginnen?

Hoe ga je trouwens van de absolute waarde naar de euclidean norm?

quote:

Op donderdag 21 november 2013 00:27 schreef Novermars het volgende:
De notatie die ik nu heb, dus met alpha en beta etc is de notatie die de hooglerares gebruikt, de x en y notatie gebruikt het boek. (dit was een opgave uit het boek). Aangezien de hooglerares mijn tentamens nakijkt, prefereer ik de eerste notatie.

Maar inhoudelijk, mee eens dat het niet klopt. Is het eventueel snel te fixen door vanaf de ongelijkheid, r5 van onder, absolute waardes te gebruiken en van de 1 die ik er bij optel om problemen te voorkomen als beta =0 is een epsilon te maken? Of kan ik beter gewoon opnieuw beginnen?

Ik zou het herschrijven.

quote:

Hoe ga je trouwens van de absolute waarde naar de euclidean norm?

Je hebt |x·y| ≤ ||x||·||y||. Zegt de dubbele naam Cauchy-Schwarz je iets?

[ Bericht 51% gewijzigd door wiskundenoob op 22-11-2013 15:29:57 ]

quote:

Op woensdag 20 november 2013 21:49 schreef Novermars het volgende:
[ afbeelding ]
Hoe kan je dit het beste aanpakken? In R¹ lukken me dit soort bewijzen wel, maar in R^k heb ik er meer moeite mee. Ik neem aan dat we de euclidean norm ergens moet gebruiken en een shitload een triangle inequalities?

EDIT: [ afbeelding ]
Iemand die een fout kan spotten? Ik denk eigenlijk dat het definiëren van c(n) overbodig is, maar ach...

Als een vector a convergeert naar een vector b, dan convergeren alle componenten van a ook naar de componenten van die van b. Als je het inproduct nu uitschrijft als een som, dan kan je dus gewoon het resultaat uit R^1 gebruiken.

Mbv factorstelling, f(x)=(x-a)g(x)+f(a) als a een reëel getal is, moet ik de nulpunten vinden van



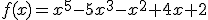
Dan is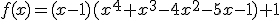

Maar hoe doe je dat? Wat ik ervan heb begrepen is dat je eerst (x-a), a is nulpunt van f(x), moet vinden. En vervolgens f(x)/(x-a) om g(x) te bepalen? En dat steeds herhalen totdat n, macht van het polynoom, 1 is zodat je alle nulpunten hebt gevonden.

[ Bericht 0% gewijzigd door wiskundenoob op 23-11-2013 12:55:05 ]

quote:

Op zaterdag 23 november 2013 12:28 schreef wiskundenoob het volgende:
Mbv factorstelling, f(x)=(x-a)g(x)+(a) moet ik de nulpunten vinden van

vinden.

Dan is

Maar hoe doe je dat? Wat ik ervan heb begrepen is dat je eerst (x-a), a is nulpunt van f(x), moet vinden. En vervolgens f(x)/(x-a) om g(x) te bepalen? En dat steeds herhalen totdat n, macht van het polynoom, 1 is zodat je alle nulpunten hebt gevonden.

Ten eerste leg je de factorstelling (met rest 0) verkeerd uit. Als (x-a) een nulpunt is van f(x) te schrijven als het product g(x)(x-a) met deg(g(x)) = deg(f(x))-1

Het hoeft niet zo te zijn dat een polynoom ontbonden kan worden in n lineaire factoren als de graad van dat polynoom n is binnen de reële getallen. Neem daarvoor eens het polynoom

h(x) = x² + 1

De discriminant van h(x) is kleiner dan 0, en dus heeft dit polynoom géén nulpunten binnen de reële getallen. Binnen de reële getallen heet dit polynoom ook wel irreducibel.

SPOILER

Om spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.

Binnen de complexe getallen heeft h(x) wel nulpunten, bekijk daarvoor eens de hoofdstelling van de algebra.

Stel dat x = a een nulpunt is van f(x), dan weten we

f(x) = (x-a)g(x) (factorstelling)

En dus

g(x) = f(x)/(x-a)

Veronderstel f(x) en (x-a) bekend, dan kun je met behulp van een polynoomstaartdeling g(x) eenvoudig berekenen.

http://www.wisfaq.nl/show3archive.asp?id=13995&j=2003

Kijk daarvoor eens hier. Als je het eenmaal snapt is het niet zo moeilijk, maar het uitleggen is best klote en laat ik ook liever aan Riparius over als hij daar tijd/zin in heeft, wellicht heeft hij zelfs een beter alternatief.


De algemene factorstelling is

f(x) = g(x)p(x) + r(x)

Nu moet je zelf even nadenken wat je kunt zeggen over de graad van de polynomen g(x), p(x) en r(x) als

g(x) het quötient heet
p(x) de deler
en r(x) de rest.

waarbij de graad van het polynoom f(x) gelijk is aan n.

[ Bericht 5% gewijzigd door Amoeba op 23-11-2013 12:53:47 ]

Respect dat jullie dit snappen, de tering zeg

quote:

Op zaterdag 23 november 2013 12:28 schreef wiskundenoob het volgende:
Mbv factorstelling, f(x)=(x-a)g(x)+f(a) als a een reëel getal is, moet ik de nulpunten vinden van



Dan is

Maar hoe doe je dat? Wat ik ervan heb begrepen is dat je eerst (x-a), a is nulpunt van f(x), moet vinden. En vervolgens f(x)/(x-a) om g(x) te bepalen? En dat steeds herhalen totdat n, macht van het polynoom, 1 is zodat je alle nulpunten hebt gevonden.

Dit polynoom heeft geen rationale nulpunten, aangezien eventuele rationale nulpunten geheel zouden moeten zijn en, afgezien van het teken, tevens delers van 2. Maar je kunt gemakkelijk nagaan dat −1, 1, −2 en 2 geen nulpunten zijn. Aangezien het een vijfdegraadspolynoom is, zijn de nulpunten in het algemeen ook niet algebraïsch uit te drukken in de coëfficiënten. Dus zou je de nulpunten numeriek moeten benaderen, maar dat lijkt me gezien de opdracht om het polynoom met behulp van de factorstelling te ontbinden ook niet de bedoeling. Controleer nog eens of je de opgave niet verkeerd hebt overgenomen.

[ Bericht 0% gewijzigd door Riparius op 23-11-2013 13:40:54 ]

quote:

Op zaterdag 23 november 2013 13:30 schreef Noppie2000 het volgende:
Respect dat jullie dit snappen, de tering zeg

Mwa, dit is allemaal eerstejaars wiskunde . En met al tekentjes als en kan het er al gauw schokkender uitzien dan dat het is.

quote:

Op vrijdag 22 november 2013 16:31 schreef thenxero het volgende:

[..]

Als een vector a convergeert naar een vector b, dan convergeren alle componenten van a ook naar de componenten van die van b. Als je het inproduct nu uitschrijft als een som, dan kan je dus gewoon het resultaat uit R^1 gebruiken.

Dat uitschrijven is nu juist overbodig als je gebruik maakt van Cauchy-Schwarz, zoals ik hierboven ook al aangeef. Het bewijs wordt dan een stuk eenvoudiger en eleganter.

quote:

Op zaterdag 23 november 2013 13:58 schreef Riparius het volgende:

[..]

Dat uitschrijven is nu juist overbodig als je gebruik maakt van Cauchy-Schwarz, zoals ik hierboven ook al aangeef. Het bewijs wordt dan een stuk eenvoudiger en eleganter.

Ja en Cauchy Schwarz is overbodig als je het wel uitschrijft. Kwestie van smaak, en altijd goed om meerdere manieren in te zien.

quote:

Op zaterdag 23 november 2013 12:38 schreef Amoeba het volgende:

De algemene factorstelling is

f(x) = g(x)p(x) + r(x)

Nu moet je zelf even nadenken wat je kunt zeggen over de graad van de polynomen g(x), p(x) en r(x) als

g(x) het quötient heet
p(x) de deler
en r(x) de rest.

waarbij de graad van het polynoom f(x) gelijk is aan n.

Nou, wat moet ik kan dan concluderen over de n van g(x), p(x) en r(x)?
Het quotiënt is n-degraads polynoom en de deler is een eerstegraads factor en r(x) heeft geen graad.

quote:

Op zaterdag 23 november 2013 13:31 schreef Riparius het volgende:

[..]

Dit polynoom heeft geen rationale nulpunten, aangezien eventuele rationale nulpunten geheel zouden moeten zijn en, afgezien van het teken, tevens delers van 2. Maar je kunt gemakkelijk nagaan dat −1, 1, −2 en 2 geen nulpunten zijn. Aangezien het een vijfdegraadspolynoom is, zijn de nulpunten in het algemeen ook niet algebraïsch uit te drukken in de coëfficiënten. Dus zou je de nulpunten numeriek moeten benaderen, maar dat lijkt me gezien de opdracht om het polynoom met behulp van de factorstelling te ontbinden ook niet de bedoeling. Controleer nog eens of je de opgave niet verkeerd hebt overgenomen.

Vb-opgave is correct overgenomen, maar ik zie nu dat a, nulpunt van f(x), wordt meegegeven. Dus de bedoeling is dat ik die veeltermen deelt door de factor.

Waarom moet je nagaan dat −1, 1, −2 en 2 nulpunten zijn? Ligt dat aan dit soort opgaves? Dat er één van die getallen vaak een nulpunt is.
En wat bedoel je precies met delers van 2?

[ Bericht 47% gewijzigd door wiskundenoob op 23-11-2013 22:52:30 ]

quote:

Op zaterdag 23 november 2013 22:08 schreef wiskundenoob het volgende:

Vb-opgave is correct overgenomen, maar ik zie nu dat a, nulpunt van f(x), wordt meegegeven. Dus de bedoeling is dat ik die veeltermen deel door de factor.

Ik denk niet dat dat de bedoeling is. Je kunt nu wel algebraïsch je veelterm delen door (x − a), maar daarmee vind je echt geen nulpunt, je weet namelijk niet wat a is.

quote:

Waarom moet je nagaan dat −1, 1, −2 en 2 nulpunten zijn? Ligt dat aan dit soort opgaves? Dat er één van die getallen vaak een nulpunt is.
En wat bedoel je precies met delers van 2?

Er is een stelling die zegt dat voor eventuele rationale nulpunten p/q van een veelterm (met p en q geheel en onderling ondeelbaar) geldt dat p een deler is van de constante term en q een deler van de coëfficiënt van de hoogste macht. Welnu, die laatste is hier 1 (de coëfficiënt van x⁵) en daaruit volgt dat eventuele rationale nulpunten van je veelterm geheel moeten zijn en, afgezien van het teken, delers van de constante term 2. Nu is 2 alleen deelbaar door 1 en door 2, en dus hoeven we alleen −1, 1, −2 en 2 te proberen als mogelijke rationale nulpunten. Maar geen van deze vier blijkt een nulpunt te zijn, en dus kunnen we met zekerheid zeggen dat je veelterm geen rationale nulpunten heeft. Als je de nulpunten van een veelterm (zowel reëel als complex) numeriek wil bepalen dan kun je dat bijvoorbeeld hier doen.

quote:

Op zaterdag 23 november 2013 23:08 schreef Riparius het volgende:

[..]

Ik denk niet dat dat de bedoeling is. Je kunt nu wel algebraïsch je veelterm delen door (x − a), maar daarmee vind je echt geen nulpunt, je weet namelijk niet wat a is.

[..]

a = 1 en dus kan je wel de rationele nulpunten vinden als die er zijn. Als er restwaarde ontstaat na het delen dan zijn er geen rationele nulpunten.

Zelfs als a niet is meegegeven dan kan je makkelijk de rationele nulpunten vinden als ik het goed begrijp.

Ik zie nu waar mijn fout zit. a is geen nulpunt van f(x). Behalve natuurlijk als f(a)=0 zodat f(x)=(x-a)g(x).

[ Bericht 2% gewijzigd door wiskundenoob op 24-11-2013 00:07:42 ]

quote:

Op zaterdag 23 november 2013 22:08 schreef wiskundenoob het volgende:

[..]

Nou, wat moet ik kan dan concluderen over de n van g(x), p(x) en r(x)?
Het quotiënt is n-degraads polynoom en de deler is een eerstegraads factor en r(x) heeft geen graad.

Nee. Ten eerste kun je niet spreken over een n van g(x), p(x) en r(x), en daarnaast bestaat 'geen graad' niet. Een constante functie heeft graad 0, namelijk.

Ten eerste geldt dat het product g(x)•p(x) graad n heeft en r(x) een graad kleiner dan n heeft.

Daarnaast hoeft r(x) niet constant te zijn, dit kan prima een polynoom zijn.

Vraag van numerieke wiskunde:

http://staff.science.uva.nl/~rstevens/oefententamen.pdf

Opgave 1a was makkelijk (nagaan dat het voor de basisfuncties van P_3 geldt, dus 1, x, x^2 en x^3. Rest volgt uit lineariteit). Opgave b lukt me niet. Ik meen me te herinneren dat het idee was om een of andere rare functie te maken, en dan heel vaak (vier keer wss) Rolle toe te passen. Om Rolle zo vaak toe te kunnen passen heb ik een functie nodig met nulpunten in [0,1]..

[ Bericht 15% gewijzigd door Hanneke12345 op 24-11-2013 14:15:37 ]

quote:

Op zondag 24 november 2013 14:08 schreef Hanneke12345 het volgende:
Vraag van numerieke wiskunde:

http://staff.science.uva.nl/~rstevens/oefententamen.pdf

Opgave 1a was makkelijk (nagaan dat het voor de basisfuncties van P_3 geldt, dus 1, x, x^2 en x^3. Rest volgt uit lineariteit). Opgave b lukt me niet. Ik meen me te herinneren dat het idee was om een of andere rare functie te maken, en dan heel vaak (vier keer wss) Rolle toe te passen. Om Rolle zo vaak toe te kunnen passen heb ik een functie nodig met nulpunten in [0,1]..

Ken je Hermite-interpolatie?

quote:

Op zondag 24 november 2013 14:08 schreef Hanneke12345 het volgende:
Vraag van numerieke wiskunde:

http://staff.science.uva.nl/~rstevens/oefententamen.pdf

Opgave 1a was makkelijk (nagaan dat het voor de basisfuncties van P_3 geldt, dus 1, x, x^2 en x^3. Rest volgt uit lineariteit). Opgave b lukt me niet. Ik meen me te herinneren dat het idee was om een of andere rare functie te maken, en dan heel vaak (vier keer wss) Rolle toe te passen. Om Rolle zo vaak toe te kunnen passen heb ik een functie nodig met nulpunten in [0,1]..

Mocht de tip van thabit niet genoeg zijn:

je hebt net iets gedaan met polynomen. Hoeveel verschillende nulpunten kan een polynoom van graad n hebben, en hoe vaak kun je daarop Rolle toepassen? (Je hebt nog wel iets extra nodig dan deze hint, dus stop vooral niet als je vastloopt )

Kan iemand mij hiermee op weg helpen?

Dat is toch gewoon toepassen van de logaritme-rekenregels?

namelijk deze:



en deze