[Bèta wiskunde] Huiswerk- en vragentopic

15=(2000-16,3v)(-5--18)^-16,68

Zou iemand 'v' kunnen vrijmaken? In micky mouse taal a.u.b (5 havo)

quote:

Op woensdag 6 november 2013 17:28 schreef Enix het volgende:
15=(2000-16,3v)(-5--18)^-16,68

Zou iemand 'v' kunnen vrijmaken? In micky mouse taal a.u.b (5 havo)

Beide kanten delen door (2x min is natuurlijk plus)

Dan krijg je:



Nu beide kanten min 2000



En dan beide kanten delen door -16,3



Dit kan je verder vereenvoudigen als je wilt.



En dit kan je in de rekenmachine invoeren als je wilt:

http://www.wolframalpha.c(...)3%29+%2B+2000%2F16.3

[ Bericht 3% gewijzigd door Ensemble op 06-11-2013 17:50:18 ]

Klopt niet volgens het antwoordenboek. Het is wiskunde A dus houd het aub een beetje simpel.

Het antwoord moet 56 zijn.

Toch bedankt voor je hulp.

quote:

Op woensdag 6 november 2013 17:52 schreef Enix het volgende:
Klopt niet volgens het antwoordenboek. Het is wiskunde A dus houd het aub een beetje simpel.

Het antwoord moet 56 zijn.

Toch bedankt voor je hulp.

Weet je zeker dat je de vergelijking dan goed hebt ingetypt? Want mijn antwoord klopt met de gegeven vergelijking.

Het klopt in ieder geval niet met v=56.

Is het dit?

Dr staat toch ook tot de macht -1,668. Dus niet -16,68...

Zucht.. Je hebt gelijk.

Bedankt voor de hulp!

quote:

Op woensdag 6 november 2013 18:01 schreef Enix het volgende:
Zucht.. Je hebt gelijk.

Bedankt voor de hulp!

Als je in mijn uitwerking van net -16.68 vervangt door -1.668 krijg je dit:

http://www.wolframalpha.c(...)3%29+%2B+2000%2F16.3

Ongeveer 56. Dus dat klopt.

quote:

Op woensdag 6 november 2013 17:52 schreef Enix het volgende:
Het is wiskunde A dus houd het aub een beetje simpel.

Heb je een grafische rekenmachine? Als ik dat zo zie, is de gedachte waarschijnlijk geweest dat je de grafieken van
Y₁ = (2000 - 16,3v)(-5 - -18)^-1,668 en Y₂ = 15 plot en het snijpunt van de grafieken bepaalt.

http://www.kaveurne.be/wiskunde/IGwiskunde2007b.pdf

Vraag 5.

Ik kom zover:

2 cos² (3x + 30°) = 1
cos² (3x + 30°) = 1/2
cos (3x + 30°) = wortel(1/2) oftewel 1/4

Nu wil ik eerst weten wat cos(x)=1/4 is, maar ik krijg dit niet voor elkaar. Ik weet wel dat de waarde van x tussen de 60 en 90 graden ligt, dat moet wel, want voor cos(60°)=1/2 en cos(90°)=0.

Ik denk niet dat de additietheorum hier zal helpen.

quote:

Op woensdag 6 november 2013 22:47 schreef DefinitionX het volgende:
http://www.kaveurne.be/wiskunde/IGwiskunde2007b.pdf

Vraag 5.

Ik kom zover:

2 cos² (3x + 30°) = 1
cos² (3x + 30°) = 1/2
cos (3x + 30°) = wortel(1/2) oftewel 1/4

Nee, hier gaat het al fout, want

1. De vierkantswortel uit 1/2 is niet 1/4

en

2. Je vergeet dat cos(3x + 30°) ook nog gelijk kan zijn aan min de vierkantswortel uit 1/2

Je hebt:

√(1/2) = √1 / √2 = 1 / √2 = √2 / 2 = ½√2.

quote:

Op woensdag 6 november 2013 22:47 schreef DefinitionX het volgende:
http://www.kaveurne.be/wiskunde/IGwiskunde2007b.pdf

Vraag 5.

Ik kom zover:

2 cos² (3x + 30°) = 1
cos² (3x + 30°) = 1/2
cos (3x + 30°) = wortel(1/2) oftewel 1/4

Nu wil ik eerst weten wat cos(x)=1/4 is, maar ik krijg dit niet voor elkaar. Ik weet wel dat de waarde van x tussen de 60 en 90 graden ligt, dat moet wel, want voor cos(60°)=1/2 en cos(90°)=0.

Ik denk niet dat de additietheorum hier zal helpen.

Ken uw goniometrische identiteiten!!

cos(2x) = cos²(x) - sin²(x) = 2cos²(x) - 1 = 1 - 2sin²(x)

... en zoals Riparius hierboven al aangeeft; houdt rekening met het feit dat a² zowel +a als -a als oplossing heeft; wel effe checken of ze beide valide zijn natuurlijk.

[ Bericht 0% gewijzigd door VanishedEntity op 07-11-2013 00:34:42 ]

Bepaal mbv de grafiek van f voor welke reële getallen x geldt dat -1 ≤ f(x) ≤1

f(x) = (-2x -2 )/(2x -1)

-1 = (-2x -2)/(2x -1)
x = -2/5

als x = 1 dan is f(x)= -4

Dus x ≥ -2/5?

1 = (-2x -2)/(2x -1)
x = -6

als x = -5 dan is f(x)= -8/11

Dus x ≤ -6?

En omdat het een gebroken lineaire functie is kan je de twee voorwaardes niet bij elkaar brengen?

[ Bericht 7% gewijzigd door wiskundenoob op 07-11-2013 00:49:14 ]

quote:

Op donderdag 7 november 2013 00:00 schreef Amoeba het volgende:
√a = a v √a = -a ja?

erhm, ja dat was best wel slordig

quote:

Op donderdag 7 november 2013 00:18 schreef wiskundenoob het volgende:
Bepaal mbv de grafiek van f voor welke reële getallen x geldt dat -1 ≤ f(x) ≤1

f(x) = -2x -2 /2x -1

-1 = -2x -2 /2x -1
x = -2/5

als x = 1 dan is f(x)= -4

Dus x ≥ -2/5?

1 = -2x -2 /2x -1
x = -6

als x = -5 dan is f(x)= -8/11

Dus x ≤ -6?

En omdat het een gebroken lineaire functie is kan je de twee voorwaardes niet bij elkaar brengen?

Bedoel je

quote:

Op donderdag 7 november 2013 00:45 schreef VanishedEntity het volgende:

[..]

Bedoel je

jep

quote:

Op donderdag 7 november 2013 00:47 schreef wiskundenoob het volgende:

[..]

jep

Daarvan zou ik maken:








knock yourself out

quote:

Op donderdag 7 november 2013 00:58 schreef VanishedEntity het volgende:

[..]

Daarvan zou ik maken:








knock yourself out

huh? Wat ben je precies aan het doen?

Oh je hebt het herleid...

De breuk in een makkelijker te hanteren vorm aan het gieten. Jij moet per slot van rekening berekenen voor welke x-waarden f(x) ts -1 en 1 ligt. Dat lijkt het mij het handigste om eerst f(x) = -1 en f(x) = 1 te berekenen.

Voor het opstellen van het tekenoverzicht zou ik wel de breuk herschrijven naar:




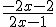
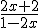
zodat je heel snel het gedrag van teller en noemer kan schetsen en kijken waar de kritische punten liggen. Je weet wat ik met een tekenoverzicht bedoel???

[ Bericht 2% gewijzigd door VanishedEntity op 07-11-2013 01:18:37 ]

quote:

Op donderdag 7 november 2013 01:08 schreef VanishedEntity het volgende:
Je weet wat ik met een tekenoverzicht bedoel???

Nope.

Waarom zou je de functie willen herleiden? x is toch gewoon makkelijk te berekenen?

En bedoel je met het schetsen van de teller en noemer gewoon de grafiek van de functie? Zoja, hoe kan ik uit die schets afleiden welke ongelijkheidtekens ik moet gebruiken?

quote:

Op woensdag 6 november 2013 22:47 schreef DefinitionX het volgende:
http://www.kaveurne.be/wiskunde/IGwiskunde2007b.pdf

Vraag 5.

Ik kom zover:

2 cos² (3x + 30°) = 1
cos² (3x + 30°) = 1/2

Ik denk niet dat de additietheorum hier zal helpen.

Ik wel. Maar eerst een opmerking: die identiteiten heten additietheorema's. Je moet er geen mengelmoes van steenkolenengels en potjeslatijn van maken, ook al heb je het voornemen om medicijnen te gaan studeren.

Ik had hierboven al laten zien dat √(1/2) = ½√2, dus je krijgt dan

cos(3x + 30°) = ½√2 ∨ cos(3x + 30°) = −½√2

Nu zou je de waarde ½√2 in ieder geval direct moeten herkennen als zijnde de cosinus (en tevens de sinus) van de 'standaardhoek' 45°, maar er zijn uiteraard meer (rotatie)hoeken waarbij de cosinus gelijk is aan ½√2, en datzelfde geldt voor −½√2. Kijk je naar de eenheidscirkel, dan vind je dat we hebben

3x + 30° = 45° + k·360° ∨ 3x + 30° = −45° + k·360° ∨ 3x + 30° = 135° + k·360° ∨ 3x + 30° = −135° + k·360°, k ∈ Z

In de uitwerking van de oplosser van Veurne kun je zien hoe je nu verder kunt gaan.

Het kan echter eleganter en overzichtelijker als je de identiteiten voor de cosinus van de dubbele hoek kent. Ik vermoed dat je die niet kent omdat je nog maar nauwelijks bent bekomen van je eerste kennismaking met de additietheorema's, dus die identiteiten gaan we nu eerst even afleiden. Je hebt

cos(α + β) = cos α·cos β − sin α·sin β

Nemen we hier β = α, dan is α + β = 2α en krijgen we dus

cos 2α = cos²α − sin²α

Naast deze identiteit voor de cosinus van de dubbele hoek zijn er nog twee andere identiteiten voor de cosinus van de dubbele hoek, die je hier gemakkelijk uit af kunt leiden als je weet dat voor elke α ook geldt

cos²α + sin²α = 1

Dat deze identiteit geldt kun je weer gemakkelijk zien aan de hand van de eenheidscirkel: je weet dat (cos α; sin α) een punt is op de eenheidscirkel dat je verkrijgt door het punt (1; 0) over een hoek α om de oorsprong te roteren. En voor de coördinaten (x; y) van elk punt op de eenheidscirkel geldt

x² + y² = 1

Immers, de afstand van het punt (x; y) tot de oorsprong is volgens Pythagoras √(x² + y²) zodat voor elk punt op de eenheidscirkel geldt √(x² + y²) = 1 en daarmee x² + y² = 1.

Uit cos²α + sin²α = 1 volgt sin²α = 1 − cos²α en cos²α = 1 − sin²α. Dus hebben we ook cos 2α = cos²α − sin²α = cos²α − (1 − cos²α) = 2·cos²α − 1 en cos 2α = cos²α − sin²α = (1 − sin²α) − sin²α = 1 − 2·sin²α. Ζο hebben we dus drie identiteiten voor de cosinus van de dubbele hoek:

cos 2α = cos²α − sin²α
cos 2α = 2·cos²α − 1
cos 2α = 1 − 2·sin²α

Voor deze opgave kunnen we nu ons voordeel doen met de tweede van deze drie identiteiten. Herleiden we het rechterlid van de goniometrische vergelijking namelijk op nul, dan hebben we

2·cos²(3x + 30°) − 1 = 0

en dus

cos(6x + 60°) = 0

Dit ziet er al een stuk handzamer uit. Als je nu weer even naar de eenheidscirkel kijkt, dan zie je dat de x-coördinaat voor een punt op de eenheidscirkel nul is in (0; 1) en in (0; −1), en dat deze punten worden bereikt als je het startpunt (1; 0) rond de oorsprong roteert over een hoek van 90° plus of min een geheel aantal halve slagen. En dus hebben we

6x + 60° = 90° + k·180°, k ∈ Z
6x = 30° + k·180°, k ∈ Z
x = 5° + k·30°, k ∈ Z

De kleinste (rotatie)hoek onder de vier gegeven alternatieven is <A> 140°, zodat k > 4 moet zijn om één van de gegeven antwoorden te krijgen. En zo zie je direct dat we met k = 5 uitkomen op <D> 155°.

[ Bericht 0% gewijzigd door Riparius op 08-11-2013 01:26:01 ]