SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Ik had vandaag tentamen Lineaire Algebra (dat ik zeker gehaald heb), en daar stond een vraag in over een reële vectorruimte V met inproduct.
Nu waren er 2 lijnen in die vectorruimte:
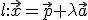
en
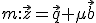
Nu was gegeven dat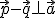
en 
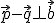
Nu was de vraag de volgende uitspraak te bewijzen:
Als bovenstaande geldt, dan geldt:
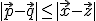
Waarbij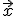
een willekeurige vector op l is, en 
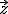een willekeurige vector op m.
Nu had ik eigenlijk een heel kort antwoord. Als geldt:
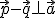en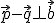
dan geldt
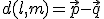
en dus
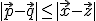
Maar nu ik hierover nadenk vind ik dit heel veel op een cirkelredenering lijken. Wat vinden jullie van mijn antwoord?
Nu waren er 2 lijnen in die vectorruimte:
en
Nu was gegeven dat
Nu was de vraag de volgende uitspraak te bewijzen:
Als bovenstaande geldt, dan geldt:
Waarbij
Nu had ik eigenlijk een heel kort antwoord. Als geldt:
dan geldt
en dus
Maar nu ik hierover nadenk vind ik dit heel veel op een cirkelredenering lijken. Wat vinden jullie van mijn antwoord?
Fervent tegenstander van het korps lasergamers.
Waarschijnlijk was het de bedoeling om gebruik te maken vanquote:Op vrijdag 1 november 2013 19:41 schreef Amoeba het volgende:
Ik had vandaag tentamen Lineaire Algebra (dat ik zeker gehaald heb), en daar stond een vraag in over een reële vectorruimte V met inproduct.
Nu waren er 2 lijnen in die vectorruimte: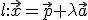
en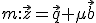
Nu was gegeven dat
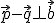
Nu was de vraag de volgende uitspraak te bewijzen:
Als bovenstaande geldt, dan geldt:
Waarbij
Nu had ik eigenlijk een heel kort antwoord. Als geldt:
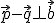
dan geldt
en dus
Maar nu ik hierover nadenk vind ik dit heel veel op een cirkelredenering lijken. Wat vinden jullie van mijn antwoord?
|| x − z ||2 = (x − z)·(x − z)
en
(p − q)·(λa − μb) = 0
Kan iemand me helpen met lim(x->0) sin(x^2)/(x*arctan(x))? Ik heb al geprobeerd met taylorbenaderingen en dan kom ik op lim(x->0) (x^2-1/6x^6+O(x^10))/(x^2-1/3x^4+O(x^6), maar weet ik niet hoe ik verder moet
.
.
Geen geknoei met Taylorbenaderingen.quote:Op vrijdag 1 november 2013 20:13 schreef tacos049 het volgende:
Kan iemand me helpen met lim(x->0) sin(x^2)/(x*arctan(x))? Ik heb al geprobeerd met taylorbenaderingen en dan kom ik op lim(x->0) (x^2-1/6x^6+O(x^10))/(x^2-1/3x^4+O(x^6), maar weet ik niet hoe ik verder moet
.
Herschrijf
sin(x2)/(x·arctan(x))
als
(sin(x2) / x2) · (x / arctan(x))
Wat denk je daarvan?
Ik zie dat sin(x^2)/x^2 1 wordt en voor x/arctan(x) zie ik niks gemakkelijks en zou ik alsnog geneigd zijn l'hopital of een benadering te gebruiken. De vraag was overigens de limiet met orde benaderingen te berekenenquote:
[..]
Geen geknoei met Taylorbenaderingen.
Herschrijf
sin(x2)/(x·arctan(x))
als
(sin(x2) / x2) · (x / arctan(x))
Wat denk je daarvan?
Beide factoren gaan naar 1 voor x → 0.quote:
[..]
Ik zie dat sin(x^2)/x^2 1 wordt en voor x/arctan(x) zie ik niks gemakkelijks en zou ik alsnog geneigd zijn l'hopital of een benadering te gebruiken. De vraag was overigens de limiet met orde benaderingen te berekenen
limx→0 x/arctan(x) = limx→0 arctan(x)/x = 1
is evengoed een standaardlimiet. Substitueer arctan(x) = θ en dus x = tan θ met |θ| < π/2, dan is
limx→0 x/arctan(x) = limθ→0 tan(θ)/θ = 1
Ik heb de eerste geprobeerd te bewijzen met de middelwaardestelling voor integralen dan zou de integraal dus gelijk zijn aan (1-0)*(1-c^2)/(3+cos(c)) voor een c tussen 0 en 1. Als ik kan laten zien dat de max kleiner is dan 2/9 en de min groter is dan 1/6 dan heb ik em bewezen, maar ik krijg de afgeleide=0 niet opgelost :/. Iemand een ander idee?
Maak gebruik van ongelijkheden.quote:
[ afbeelding ]
Ik heb de eerste geprobeerd te bewijzen met de middelwaardestelling voor integralen dan zou de integraal dus gelijk zijn aan (1-0)*(1-c^2)/(3+cos(c)) voor een c tussen 0 en 1. Als ik kan laten zien dat de max kleiner is dan 2/9 en de min groter is dan 1/6 dan heb ik em bewezen, maar ik krijg de afgeleide=0 niet opgelost :/. Iemand een ander idee?
a) Je hebt 0 < cos x < 1 voor 0 < x < 1 en dus
(1 − x2)/4 < (1 − x2)/(3 + cos x) < (1 − x2)/3 voor 0 < x < 1
b) Haal bij de integrand een factor x4 voor het wortelteken, dan zie je dat
x3 < x3√(1 + x−3) < x3√2 voor 2 < x < 3
Bedankt ik begrijp em nuquote:
[..]
Maak gebruik van ongelijkheden.
a) Je hebt 0 < cos x < 1 voor 0 < x < 1 en dus
(1 − x2)/4 < (1 − x2)/(3 + cos x) < (1 − x2)/3 voor 0 < x < 1
b) Haal bij de integrand een factor x4 voor het wortelteken, dan zie je dat
x3 < x3√(1 + x−3) < x3√2 voor 2 < x < 3
(ze hadden de de integraal van b nog beter kunnen benaderen volgens jouw methode bij b, maar dat ziet er natuurlijk wat lelijker uit)
Ik heb een vraagje lokale extreme waarden:
Het gaat om de functie: (1+2/x)*sqrt(x+6)
Van deze functie worden de lokale extreme waarden gevraagd. Deze functie is gedefinieerd voor x groter of gelijk aan -6 en x ongelijk aan 0. Voor de lokale extreme waarden kan je dan de eerste afgeleide vd functie bepalen en gelijk stellen aan nul en vervolgens de first-derivative test toepassen. Dat lukt ook allemaal wel, maar nu zit ik met het punt x = -6. Zelf dacht ik dat je daar niet zoveel over kon zeggen aan de hand van de first-derivative test, maar het antwoordenboek zegt dat je aan de hand van de first-derivative test kan concluderen dat x = -6 een lokaal minimum is. Kan iemand mij verlichten met hoe je dat kan concluderen?
Het gaat om de functie: (1+2/x)*sqrt(x+6)
Van deze functie worden de lokale extreme waarden gevraagd. Deze functie is gedefinieerd voor x groter of gelijk aan -6 en x ongelijk aan 0. Voor de lokale extreme waarden kan je dan de eerste afgeleide vd functie bepalen en gelijk stellen aan nul en vervolgens de first-derivative test toepassen. Dat lukt ook allemaal wel, maar nu zit ik met het punt x = -6. Zelf dacht ik dat je daar niet zoveel over kon zeggen aan de hand van de first-derivative test, maar het antwoordenboek zegt dat je aan de hand van de first-derivative test kan concluderen dat x = -6 een lokaal minimum is. Kan iemand mij verlichten met hoe je dat kan concluderen?
x = -6 is een randpunt van je functie f. Waarschijnlijk concludeer je dat f'(x) > 0 rond x = -6, dus een lokaal minimum.quote:
Ik heb een vraagje lokale extreme waarden:
Het gaat om de functie: (1+2/x)*sqrt(x+6)
Van deze functie worden de lokale extreme waarden gevraagd. Deze functie is gedefinieerd voor x groter of gelijk aan -6 en x ongelijk aan 0. Voor de lokale extreme waarden kan je dan de eerste afgeleide vd functie bepalen en gelijk stellen aan nul en vervolgens de first-derivative test toepassen. Dat lukt ook allemaal wel, maar nu zit ik met het punt x = -6. Zelf dacht ik dat je daar niet zoveel over kon zeggen aan de hand van de first-derivative test, maar het antwoordenboek zegt dat je aan de hand van de first-derivative test kan concluderen dat x = -6 een lokaal minimum is. Kan iemand mij verlichten met hoe je dat kan concluderen?
En met 'rond' bedoel ik groter dan x = -6, maar wel in de omgeving van.
Kijk hier even:
http://www.google.nl/url?(...)Ro6ljvxh5MxwWSWvYMiA
Fervent tegenstander van het korps lasergamers.
Ah, ik lees het ja. Bedankt!quote:Op zondag 3 november 2013 11:07 schreef Amoeba het volgende:
[..]
x = -6 is een randpunt van je functie f. Waarschijnlijk concludeer je dat f'(x) > 0 rond x = -6, dus een lokaal minimum.
En met 'rond' bedoel ik groter dan x = -6, maar wel in de omgeving van.
Kijk hier even:
http://www.google.nl/url?(...)Ro6ljvxh5MxwWSWvYMiA
http://www.kaveurne.be/wiskunde/wiskunde.htm
Examen 2008 deel 1, vraag 3. Ik heb het antwoord goed, maar ik wil weten of ik juist redeneer:
335*3=1005
+75= 1080
Daar zit 3 keer 360 in. Om cos(x)=1 te krijgen zul je cos 0 cq 360 graden moeten hebben. Ongeacht hoevaak je 360 graden draait, je komt op dezelfde plek op de eenheidscirkel, namelijk voor 0 of 360 graden graden.
Ik heb nog niet gonio. vergelijkingen bestudeerd, maar ik geloof dat het oplossen op deze manier gaat.
Examen 2008 deel 1, vraag 3. Ik heb het antwoord goed, maar ik wil weten of ik juist redeneer:
335*3=1005
+75= 1080
Daar zit 3 keer 360 in. Om cos(x)=1 te krijgen zul je cos 0 cq 360 graden moeten hebben. Ongeacht hoevaak je 360 graden draait, je komt op dezelfde plek op de eenheidscirkel, namelijk voor 0 of 360 graden graden.
Ik heb nog niet gonio. vergelijkingen bestudeerd, maar ik geloof dat het oplossen op deze manier gaat.
Dat is juist jaquote:
http://www.kaveurne.be/wiskunde/wiskunde.htm
Examen 2008 deel 1, vraag 3. Ik heb het antwoord goed, maar ik wil weten of ik juist redeneer:
335*3=1005
+75= 1080
Daar zit 3 keer 360 in. Om cos(x)=1 te krijgen zul je cos 0 cq 360 graden moeten hebben. Ongeacht hoevaak je 360 graden draait, je komt op dezelfde plek op de eenheidscirkel, namelijk voor 0 of 360 graden graden.
Ik heb nog niet gonio. vergelijkingen bestudeerd, maar ik geloof dat het oplossen op deze manier gaat.
cos(pi/12)
cos(pi/12)=cos(pi/4 - pi/6)=cos(pi/4)*sin(pi/6) - cos(pi/6)*sin(pi/4)
Ik ben uitgegaan van wat die video deed, maar dan voor de cosinus. Volgens mij is het niet goed.
[ Bericht 4% gewijzigd door DefinitionX op 05-11-2013 19:00:01 ]
cos(pi/12)=cos(pi/4 - pi/6)=cos(pi/4)*sin(pi/6) - cos(pi/6)*sin(pi/4)
Ik ben uitgegaan van wat die video deed, maar dan voor de cosinus. Volgens mij is het niet goed.
[ Bericht 4% gewijzigd door DefinitionX op 05-11-2013 19:00:01 ]
Nee, voor de cosinus is de regel net iets anders:quote:
cos(pi/12)
cos(pi/12)=cos(pi/4 - pi/6)=cos(pi/4)*sin(pi/6) - cos(pi/6)*sin(pi/4)
Klopt dit? Ik ben uitgegaan van wat die video deed, maar dan voor de cosinus.
cos(x-y) = cos(x)cos(y)+sin(x)sin(y)
Deze regels kun je ook zelf afleiden door de cosinus/sinus om te schrijven naar e-machten:
En deze e-machten vervolgens weer om te schrijven naar cosinussen/sinussen en dan de haakjes uit te werken (dat wordt me wat veel werk om uit te schrijven
)[ Bericht 25% gewijzigd door Alrac4 op 05-11-2013 19:16:40 ]
Het is van belang dat je de zogeheten additietheorema's voor de cosinus en de sinus van de som en het verschil van twee (rotatie)hoeken goed kent. Deze identiteiten luiden als volgtquote:
cos(pi/12)
Ik ben uitgegaan van wat die video deed, maar dan voor de cosinus. Volgens mij is het niet goed.
cos(α + β) = cos α∙cos β − sin α∙sin β
cos(α − β) = cos α∙cos β + sin α∙sin β
sin(α + β) = sin α∙cos β + cos α∙sin β
sin(α − β) = sin α∙cos β − cos α∙sin β
Als je een algemeen geldig bewijs wil zien voor deze identiteiten uitgaande van de definities voor de cosinus en de sinus aan de hand van de eenheidscirkel, dan kan ik je aanraden mijn PDF hierover eens te bestuderen.
Dan ga je ervan uit dat de vragensteller wel de formule van Euler kent, maar dat is voor zover ik weet niet het geval. Het gaat trouwens veel eenvoudiger met complexe getallen als je weet dat argumenten optellen (modulo 2π) bij vermenigvuldiging van complexe getallen. Een vermenigvuldiging met cos θ + i·sin θ beantwoordt aan een rotatie om de oorsprong over een hoek θ in het complexe vlak, en dus hebben wequote:
En deze e-machten vervolgens weer om te schrijven naar cosinussen/sinussen en dan de haakjes uit te werken (dat wordt me wat veel werk om uit te schrijven
cos(α + β) + i∙sin(α + β) = (cos α + i∙sin α)(cos β + i∙sin β)
Uitwerken van de haakjes in het rechterlid en gebruik maken van i2 = −1 levert dan
cos(α + β) + i∙sin(α + β) = (cos α∙cos β − sin α∙sin β) + i∙(sin α∙cos β + cos α∙sin β)
en gelijkstellen van de reële en imaginaire delen geeft dan direct
cos(α + β) = cos α∙cos β − sin α∙sin β
sin(α + β) = sin α∙cos β + cos α∙sin β
Verder is α − β = α + (−β) en cos(−β) = cos β en tevens sin(−β) = −sin β, zodat ook
cos(α − β) = cos α∙cos β + sin α∙sin β
sin(α − β) = sin α∙cos β − cos α∙sin β
Ik moet laten zien dat als y = f(u) en u = g(x), en f en g zijn beide twee keer differentieerbaar, dat:
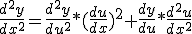
Nu ben ik eerst begonnen met de kettingregel voor de eerste afgeleide:
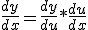
Daarna:
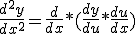
Dit is dus de productregel:
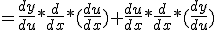
Nu lukt het mij nog om dat eerste deel samen te nemen tot:
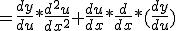
De vraag:
Maar ik snap niet hoe ze van dat tweede deel na de plus:
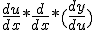
naar:
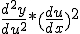
komen.
Heeft er iemand een idee?
Nu ben ik eerst begonnen met de kettingregel voor de eerste afgeleide:
Daarna:
Dit is dus de productregel:
Nu lukt het mij nog om dat eerste deel samen te nemen tot:
De vraag:
Maar ik snap niet hoe ze van dat tweede deel na de plus:
naar:
komen.
Heeft er iemand een idee?
Simpelweg nog een keer de kettingregel toepassen:quote:
Ik moet laten zien dat als y = f(u) en u = g(x), en f en g zijn beide twee keer differentieerbaar, dat:
Nu ben ik eerst begonnen met de kettingregel voor de eerste afgeleide:
Daarna:
Dit is dus de productregel:
Nu lukt het mij nog om dat eerste deel samen te nemen tot:
De vraag:
Maar ik snap niet hoe ze van dat tweede deel na de plus:
naar:
komen.
Heeft er iemand een idee?
The biggest argument against democracy is a five minute discussion with the average voter.
Ah oke, dan snap ik hem. Bedankt.quote:Op dinsdag 5 november 2013 22:55 schreef M.rak het volgende:
[..]
Simpelweg nog een keer de kettingregel toepassen:
Kan iemand mij vertellen waarom je bij gebroken lineaire functies de verticale en horizontale asymptoten wil weten?
[ Bericht 1% gewijzigd door wiskundenoob op 06-11-2013 00:02:48 ]
[ Bericht 1% gewijzigd door wiskundenoob op 06-11-2013 00:02:48 ]
Gewoon, omdat het kan, en omdat we jou daar dan lekker lastige vragen over kunnen stellen. En ze zijn handig als je de grafiek van een functie gaat schetsen. Maar ja, wie doet dat tegenwoordig nog met potlood en (ruitjes)papier?quote:
Kan iemand mij vertellen waarom je bij gebroken lineaire functies de verticale en horizontale asymptoten wil weten?
Om maar een banaal voorbeeld te geven.quote:
Kan iemand mij vertellen waarom je bij gebroken lineaire functies de verticale en horizontale asymptoten wil weten?
Stel je wilt harder gaan. Maar wat blijkt, hoe harder je gaat, hoe minder je energie wordt omgezet in feitelijke snelheid. Deze relatie blijkt een asymptoot te hebben, waar ligt die?
ant: bij lichtsnelheid
Nu hopen dat ik dit niet fout heb verteld
