SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Ik ga over 'n paar weken proefstuderen in Utrecht voor de studie wiskunde (en toepassingen). Toevallig iemand hier met ervaringen over Nederlandse wiskunde studies, met name Utrecht (of Nijmegen)? Waar moet ik (niet) op letten, bij wiskunde?
In Utrecht spreekt het me wel aan dat ik veel keuzevrijheid heb en kan switchen naar wiskunde en toepassingen mocht de pure theoretische (afleidingen, historie) kant me geen voldoening geven.
(Vond deze vraag geen apart topic waard en hoop hier wat reacties te kunnen krijgen erop.)
In Utrecht spreekt het me wel aan dat ik veel keuzevrijheid heb en kan switchen naar wiskunde en toepassingen mocht de pure theoretische (afleidingen, historie) kant me geen voldoening geven.
(Vond deze vraag geen apart topic waard en hoop hier wat reacties te kunnen krijgen erop.)
Als we aannemen dat l1 en l2 reëel zijn en je vierkantsvergelijking heeft twee reële wortels λ1 en λ2, dan zijn deze beide negatief als λ1 + λ2 < 0 en tevens λ1λ2 > 0, dusquote:Op dinsdag 29 oktober 2013 18:50 schreef Dale. het volgende:
-edit-
Sorry beetje in de war...
Wat ik wil is dat de oplossingenvan de kwadratische vergelijking
een negatief reëel deel hebben.
l2 - l1 + 1 > 0 ∧ 4l1 - l2 - 2 > 0
Heeft de vierkantsvergelijking twee toegevoegd complexe wortels, dan zijn de reële delen hiervan negatief als de som λ1 + λ2 negatief is, dus
l2 - l1 + 1 > 0
Helpt dit?
Nee, dat kan niemand, want je geeft niet aan wat er wordt gesommeerd ...quote:Op dinsdag 29 oktober 2013 20:15 schreef ronaldoo12 het volgende:
70
∑
k=10
kan iemand me helpen met wat hier uitkomt ?
Het eerste stukje begrijp ik inderdaad, als l2 - l1 + 1 > 0 ∧ 4l1 - l2 - 2 > 0 dat dan inderdaad de waardes van λ kleiner zijn dan 0.
Het tweede stukje niet helemaal... Ik snap dat als er complexe wortels zijn dat als reële delen negatief zijn dat dan λ1 + λ2 negatief is. Alleen waarom geldt l2 - l1 + 1 > 0 dan?
Voor het eerste stukje krijg ik nu:
l2 > l1 - 1 ∧ l2 < 2(2l1 - 1) dus l1 - 1 < l2 < 2(2l1 - 1) dus l1 - 1 < 2(2l1 - 1) impliceert dat l1 > 1/3
Dus voor l1 > 1/3 geldt dat l2 ligt in l1 - 1 < l2 < 2(2l1 - 1).
En nu moet je dus nog de case bepalen voor wanneer l1 ≤ 1/3 wat dus is als er complexe wortels zijn?
Het tweede stukje niet helemaal... Ik snap dat als er complexe wortels zijn dat als reële delen negatief zijn dat dan λ1 + λ2 negatief is. Alleen waarom geldt l2 - l1 + 1 > 0 dan?
Voor het eerste stukje krijg ik nu:
l2 > l1 - 1 ∧ l2 < 2(2l1 - 1) dus l1 - 1 < l2 < 2(2l1 - 1) dus l1 - 1 < 2(2l1 - 1) impliceert dat l1 > 1/3
Dus voor l1 > 1/3 geldt dat l2 ligt in l1 - 1 < l2 < 2(2l1 - 1).
En nu moet je dus nog de case bepalen voor wanneer l1 ≤ 1/3 wat dus is als er complexe wortels zijn?
http://en.wikipedia.org/w(...)lynomial_expressionsquote:
70
∑
k=10
kan iemand me helpen met wat hier uitkomt ?
70quote:
[..]
Nee, dat kan niemand, want je geeft niet aan wat er wordt gesommeerd ...
∑
k=10
(7k − 2)
Je hebt een rekenkundige reeks. Heeft een rekenkundige reeks n termen en is de eerste term t1 en de laatste term tn, dan is de som S = ½n(t1 + tn).quote:
Hier heb je n = 61, t1 = 68, tn = 488, dus S = ½·61·(68 + 488) = 16958.
quote:
[ afbeelding ]
ehmm.. wordt dit dan: 70+(7k-2)-10 ? ...
hoe kom je aan t1 en tn ?quote:
[..]
Je hebt een rekenkundige reeks. Heeft een rekenkundige reeks n termen en is de eerste term t1 en de laatste term tn, dan is de som S = ½n(t1 + tn).
Hier heb je n = 61, t1 = 68, tn = 488, dus S = ½·61·(68 + 488) = 16958.
Als λ1 en λ2 de wortels zijn van de vierkantsvergelijkingquote:
Het eerste stukje begrijp ik inderdaad, als l2 - l1 + 1 > 0 ∧ 4l1 - l2 - 2 > 0 dat dan inderdaad de waardes van λ kleiner zijn dan 0.
Het tweede stukje niet helemaal... Ik snap dat als er complexe wortels zijn dat als reële delen negatief zijn dat dan λ1 + λ2 negatief is. Alleen waarom geldt l2 - l1 + 1 > 0 dan?
λ2 + pλ + q = 0
dan geldt
λ1 + λ2 = −p, λ1λ2 = q
Zijn de wortels reëel, dan is de voorwaarde voor twee negatieve reële wortels λ1 + λ2 < 0 en tevens λ1λ2 > 0 en dus p > 0 en tevens q > 0.
Zijn de wortels λ1 en λ2 toegevoegd complex, dan is λ1 = α + βi en λ2 = α − βi waarbij α en β reëel zijn. De voorwaarde dat het reële deel α van de beide wortels negatief is, is dan equivalent met 2α = λ1 + λ2 = −p < 0 en dus p > 0. Merk op dat nu λ1λ2 = α2 + β2 > 0, zodat de voorwaarde λ1λ2 = q > 0 hier redundant is.
Je uiteindelijke voorwaarde wordtquote:Voor het eerste stukje krijg ik nu:
l2 > l1 - 1 ∧ l2 < 2(2l1 - 1) dus l1 - 1 < l2 < 2(2l1 - 1) dus l1 - 1 < 2(2l1 - 1) impliceert dat l1 > 1/3
Dus voor l1 > 1/3 geldt dat l2 ligt in l1 - 1 < l2 < 2(2l1 - 1).
En nu moet je dus nog de case bepalen voor wanneer l1 ≤ 1/3 wat dus is als er complexe wortels zijn?
(p > 0 ∧ q > 0 ∧ p2 − 4q ≥ 0) ∨ (p > 0 ∧ p2 − 4q < 0)
met p = l2 − l1 + 1 en q = 4l1 − l2 − 2
Ik heb een vraag over Lineaire Algebra 1.
Gegeven zijn de 2x2 matrices A en B. Bewijs dat de kolommenruimte van AB bevat is in de kolommenruimte van A.
Nou, stel
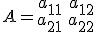en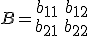 
dan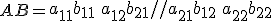
Nou, dit laatste lukt al helemaal waardeloos. Enfin, voor de // staat de bovenste rij, na de // staat de onderste rij.
Hoe laat ik nu het gevraagde zien? De kolommenruimte van A is 1,2 of 0. Wanneer die 0 is dan zijn alle a'tjes 0, en is dus de kolommenruimte van AB ook 0, immers is AB dan de nulmatrix.
Als de kolommenruimte van A 1 is dan is er één kolom, en we zien dan in AB ook wéér een nulkolom terug.
Als de kolommenruimte van A gelijk is aan 2 ....
Maar wat als de rijenruimte van B nu eens 1 is?
Ik snap hier echt helemaal niets van.
Gegeven zijn de 2x2 matrices A en B. Bewijs dat de kolommenruimte van AB bevat is in de kolommenruimte van A.
Nou, stel
dan
Nou, dit laatste lukt al helemaal waardeloos. Enfin, voor de // staat de bovenste rij, na de // staat de onderste rij.
Hoe laat ik nu het gevraagde zien? De kolommenruimte van A is 1,2 of 0. Wanneer die 0 is dan zijn alle a'tjes 0, en is dus de kolommenruimte van AB ook 0, immers is AB dan de nulmatrix.
Als de kolommenruimte van A 1 is dan is er één kolom, en we zien dan in AB ook wéér een nulkolom terug.
Als de kolommenruimte van A gelijk is aan 2 ....
Maar wat als de rijenruimte van B nu eens 1 is?
Ik snap hier echt helemaal niets van.
Fervent tegenstander van het korps lasergamers.
LaTeX-hint:quote:Op dinsdag 29 oktober 2013 23:02 schreef Amoeba het volgende:
Ik heb een vraag over Lineaire Algebra 1.
Gegeven zijn de 2x2 matrices A en B. Bewijs dat de kolommenruimte van AB bevat is in de kolommenruimte van A.
Nou, stel
dan
Nou, dit laatste lukt al helemaal waardeloos. Enfin, voor de // staat de bovenste rij, na de // staat de onderste rij.
Hoe laat ik nu het gevraagde zien? De kolommenruimte van A is 1,2 of 0. Wanneer die 0 is dan zijn alle a'tjes 0, en is dus de kolommenruimte van AB ook 0, immers is AB dan de nulmatrix.
Als de kolommenruimte van A 1 is dan is er één kolom, en we zien dan in AB ook wéér een nulkolom terug.
Als de kolommenruimte van A gelijk is aan 2 ....
Maar wat als de rijenruimte van B nu eens 1 is?
Ik snap hier echt helemaal niets van.
Wiskunde-hint: interpreteer een matrix als een lineaire afbeelding.
quote:
[..]
LaTeX-hint:
Wiskunde-hint: interpreteer een matrix als een lineaire afbeelding.
Ik heb nog een vraag, niet over de uitwerking, maar hoe ver moet ik dit oplossen?
Gegeven is een stelsel vergelijkingen met 3 variabelen en een parameter a. De vraagstelling luidt: los het volgende stelsel vergelijkingen op voor iedere waarde van a.
Nu heb ik het geschreven als
Ax = b
En dus x = A-1b voor iedere waarde van a waarvoor A inverteerbaar is (dus determinant ongelijk 0 ). Verder heb ik de waarden voor a bekeken waarvoor A niet inverteerbaar is.
Moet ik nu op het tentamen die inverse van A ook nog bepalen, of hoeft dat niet denk je?
Fervent tegenstander van het korps lasergamers.
De matrix A kun je zien als een afbeelding van R2 naar R2 die v naar Av stuurt. De kolomruimte is niets anders dan het beeld van deze afbeelding, d.w.z. alle vectoren die daadwerkelijk van de vorm Av zijn. De matrix AB is als afbeelding gelijk aan B gevolgd door A: (AB)v = A(Bv). Alles wat van geschreven kan worden als ABv kan dus ook zeker geschreven worden als Aw (nl met w = Bv). Daarom is het beeld van AB bevat in het beeld van A.
