[Bèta wiskunde] Huiswerk- en vragentopic

zondag 27 oktober 2013 @ 14:48:22 #52

DefinitionX

http://www.kaveurne.be/wiskunde/wiskunde.htm

Examen 2009 a/juli, vraag 1.

Ik heb dit opgelost met de cosinusregel. Echter, waarom zou hier een sinusregel niet werken?

Ik weet de waarde van sin30, dat is 1/2. Nu kan ik ook de waarde van hoek c berekenen door overstaande/schuine zijde. Ik weet dan weliswaar niet hoeveel graden, maar wel de delingsquotient ervan. Als ik dat invul in de sinusregel:

hoek c= (2/wortel 3) gedeeld door (2) dat is wortel 3.

sinusA/BC = sinus C/AB
0.5/BC=wortel 3/(wortel3/2)=2

Maar nu ik terugdenk......Deze driehoek is geen rechthoekige driehoek dus hoe ik hoek c bereken klopt niet.

Het antwoord is B:

BC^2 = AC^2 + AB^2 - 2*AC*AB*cos(30)

zondag 27 oktober 2013 @ 15:04:00 #53

Riparius

quote:
Op zondag 27 oktober 2013 14:48 schreef DefinitionX het volgende:
http://www.kaveurne.be/wiskunde/wiskunde.htm

Examen 2009 a/juli, vraag 1.

Ik heb dit opgelost met de cosinusregel. Echter, waarom zou hier een sinusregel niet werken?

Om de lengte van een zijde van een driehoek met behulp van de sinusregel te berekenen moet je twee hoeken van de driehoek kennen. Maar hier is slechts de grootte van één hoek gegeven, dus kun je de sinusregel hier niet gebruiken.

Sinusregel:

a : sin α = b : sin β = c : sin γ

Cosinusregel:

a² = b² + c² − 2bc·cos α
b² = c² + a² − 2ca·cos β
c² = a² + b² − 2ab·cos γ

[ Bericht 29% gewijzigd door Riparius op 27-10-2013 18:19:54 ]

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

zondag 27 oktober 2013 @ 20:08:52 #54

DefinitionX

Dank u wel voor het verhelderen van de vraag over de cosinusregel Riparius.

Vraag 5 examen 2008 augustus/b: http://www.kaveurne.be/wiskunde/wiskunde.htm

Ik begrijp dat ik hier met stelsels moet werken. Ik kom niet verder dan 10b-c=34 te stellen als eerste vergelijking, maar ik weet niet welke andere vergelijking ik kan stellen om de waarde van b en c te berekenen.. Naar de uitwerking van vraag 5 kijkend snap ik niet zo goed hoe de oplosser komt aan b^2-c=9.

zondag 27 oktober 2013 @ 20:20:25 #55

Riparius

quote:
Op zondag 27 oktober 2013 20:08 schreef DefinitionX het volgende:
Dank u wel voor het verhelderen van de vraag over de cosinusregel Riparius.

Vraag 5 examen 2008 augustus/b: http://www.kaveurne.be/wiskunde/wiskunde.htm

Ik begrijp dat ik hier met stelsels moet werken. Ik kom niet verder dan 10b-c=34 te stellen als eerste vergelijking, maar ik weet niet welke andere vergelijking ik kan stellen om de waarde van b en c te berekenen.. Naar de uitwerking van vraag 5 kijkend snap ik niet zo goed hoe de oplosser komt aan b^2-c=9.

Beetje analytische meetkunde. Je moet voor deze opgave weten dat de vergelijking van een cirkel met middelpunt (p;q) en straal r is te schrijven als

(x − p)² + (y − q)² = r²

Herleiden van de gegeven vergelijking tot een vergelijking van deze gedaante (waarbij je kwadraatafsplitsing moet gebruiken) levert dan op dat

b² − c = 9

aangezien is gegeven dat de straal van de cirkel 3 is. Het gegeven dat het punt (5;3) op de cirkel ligt levert een tweede betrekking op tussen b en c, namelijk

10b − c = 34

Oplossen van dit stelsel geeft dan b = 5, c = 16, en dus b + c = 21.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

zondag 27 oktober 2013 @ 21:18:20 #56

DefinitionX

Dank u!

zondag 27 oktober 2013 @ 22:37:19 #57

#ANONIEM

Kan iemand mij de stappen uitleggen hoe ik de afgeleide krijg van een wortel en dan staat er binnen de wortel (x^2-1)/(x) Ik weet dat het iets is met de ketting regel en coëfficiënt regel.

[ Bericht 0% gewijzigd door #ANONIEM op 27-10-2013 22:37:37 ]

zondag 27 oktober 2013 @ 22:46:43 #58

randomo

quote:
Op zondag 27 oktober 2013 22:37 schreef MCH het volgende:
Kan iemand mij de stappen uitleggen hoe ik de afgeleide krijg van een wortel en dan staat er binnen de wortel (x^2-1)/(x) Ik weet dat het iets is met de ketting regel en coëfficiënt regel.

Als je weet wat de ketting- en quotiëntregel inhouden, zou het toepassen ook moeten lukken. Het berekenen van een afgeleide is alleen maar het toepassen van de regels. Je moet even wat meer toelichting geven.
Wat precies begrijp je niet? Hoever kom je nu?

zondag 27 oktober 2013 @ 23:01:20 #59

Riparius

quote:
Op zondag 27 oktober 2013 22:37 schreef MCH het volgende:
Kan iemand mij de stappen uitleggen hoe ik de afgeleide krijg van een wortel en dan staat er binnen de wortel (x^2-1)/(x) Ik weet dat het iets is met de ketting regel en coëfficiënt regel.

Als je de vierkantswortel bedoelt uit (x² − 1)/x = x − x⁻¹ dan heb je dus

f(x) = (x − x⁻¹)^1/2

Nu lukt het toch wel om hiervan de afgeleide te bepalen? En wat versta je onder coëfficiëntregel?

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

zondag 27 oktober 2013 @ 23:03:26 #60

#ANONIEM

quote:
Op zondag 27 oktober 2013 23:01 schreef Riparius het volgende:

[..]

Als je de vierkantswortel bedoelt uit (x² − 1)/x = x − x⁻¹ dan heb je dus

f(x) = (x − x⁻¹)^1/2

Nu lukt het toch wel om hiervan de afgeleide te bepalen? En wat versta je onder coëfficiëntregel?

De afgeleide van een breuk. Sorry, ik krijg wiskunde in het Engels.

zondag 27 oktober 2013 @ 23:07:07 #61

Riparius

quote:
Op zondag 27 oktober 2013 23:03 schreef MCH het volgende:

[..]

De afgeleide van een breuk. Sorry, ik krijg wiskunde in het Engels.

Dan bedoel je de quotiëntregel. In het Engels is dat de quotient rule, dus ik zie niet waarom je de termen quotiënt en coëfficiënt door elkaar gooit. Ik zou trouwens de quotiëntregel hier niet gebruiken, onnodig ingewikkeld.

[ Bericht 2% gewijzigd door Riparius op 29-10-2013 16:52:16 ]

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

zondag 27 oktober 2013 @ 23:07:46 #62

#ANONIEM

http://nl.tinypic.com/r/fa60yu/5

Hier staat de uitwerking waar ik dus geen hout van kan snijden.

zondag 27 oktober 2013 @ 23:12:08 #63

Riparius

quote:
Op zondag 27 oktober 2013 23:07 schreef MCH het volgende:
http://nl.tinypic.com/r/fa60yu/5

Hier staat de uitwerking waar ik dus geen hout van kan snijden.

Hier wordt inderdaad de quotiëntregel en de kettingregel gebruikt, nadat eerst nog het domein van de functie is bepaald. Als je de regels voor het differentiëren goed kent is hier verder niet zoveel aan te snappen. Maar kennelijk begrijp je die regels nog niet voldoende. Maar goed, zoals gezegd, ik zou het zo niet doen.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

zondag 27 oktober 2013 @ 23:16:51 #64

#ANONIEM

quote:
Op zondag 27 oktober 2013 23:12 schreef Riparius het volgende:

[..]

Hier wordt inderdaad de quotiëntregel en de kettingregel gebruikt, nadat eerst nog het domein van de functie is bepaald. Als je de regels voor het differentiëren goed kent is hier verder niet zoveel aan te snappen. Maar kennelijk begrijp je die regels nog niet voldoende. Maar goed, zoals gezegd, ik zou het zo niet doen.

Maar staat hier nu hetzelfde als 0,5wortel(u)^-0,5 keer de afgeleide van u ? Alleen dan weer herschreven volgens algebraïsche regels?

[ Bericht 0% gewijzigd door #ANONIEM op 27-10-2013 23:17:29 ]

zondag 27 oktober 2013 @ 23:25:44 #65

Riparius

quote:
Op zondag 27 oktober 2013 23:16 schreef MCH het volgende:

[..]

Maar staat hier nu hetzelfde als 0,5wortel(u)^-0,5 keer de afgeleide van u ? Alleen dan weer herschreven volgens algebraïsche regels?

Je kunt inderdaad u = x − x⁻¹ nemen. Maar ik zou het zo doen:

d((x − x⁻¹)^1/2)/dx = d((x − x⁻¹)^1/2)/d(x − x⁻¹) · d(x − x⁻¹)/dx = ½·(x − x⁻¹)^−1/2·(1 + x⁻²)

Dit kun je uiteraard nog verder herleiden. Je uitwerking klopt trouwens niet helemaal omdat √x niet reëel is voor x < 0.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

zondag 27 oktober 2013 @ 23:28:33 #66

#ANONIEM

quote:
Op zondag 27 oktober 2013 23:25 schreef Riparius het volgende:

[..]

Je kunt inderdaad u = x − x⁻¹ nemen. Maar ik zou het zo doen:

d((x − x⁻¹)^1/2)/dx = d((x − x⁻¹)^1/2)/d(x − x⁻¹) · d(x − x⁻¹)/dx = œ·(x − x⁻¹)^−1/2·(1 + x⁻²)

Dit kun je uiteraard nog verder herleiden. Je uitwerking klopt trouwens niet helemaal omdat √x niet reëel is voor x < 0.

Dit is niet mijn uitwerking. Dit zijn uitwerkingen van de docenten van de uni. Tot zover hun niveau, mocht dit niet totaal kloppen.

zondag 27 oktober 2013 @ 23:31:24 #67

Riparius

quote:
Op zondag 27 oktober 2013 23:28 schreef MCH het volgende:

[..]

Dit is niet mijn uitwerking. Dit zijn uitwerkingen van de docenten van de uni. Tot zover hun niveau, mocht dit niet totaal kloppen.

Als een docent van de uni dat zo opschrijft zou die persoon ontslagen mogen worden wat mij betreft.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

zondag 27 oktober 2013 @ 23:33:05 #68

#ANONIEM

quote:
Op zondag 27 oktober 2013 23:31 schreef Riparius het volgende:

[..]

Als een docent van de uni dat zo opschrijft zou die persoon ontslagen mogen worden wat mij betreft.

Jammer dat ik zelf niet zo goed onderlegd ben om ze hiermee te confronteren.

maandag 28 oktober 2013 @ 15:16:18 #69

DefinitionX

Tot nu toe geniet ik met volle teugen van "Toegepaste Wiskunde voor het hoger onderwijs (Blankespoort, de Joode en Sluijter)". Ik zit nu met limieten en er is een vraag bij me opgekomen, namelijk: zou een functie niet meer dan 1 verticale/horizontale asymptoot kunnen hebben? Neem de helft van een small eclips . Volgens mij heb je boven de eclips een verticale asymptoot, maar ook daaronder.

maandag 28 oktober 2013 @ 15:38:45 #70

Riparius

quote:
Op maandag 28 oktober 2013 15:16 schreef DefinitionX het volgende:
Tot nu toe geniet ik met volle teugen van "Toegepaste Wiskunde voor het hoger onderwijs (Blankespoort, de Joode en Sluijter)". Ik zit nu met limieten en er is een vraag bij me opgekomen, namelijk: zou een functie niet meer dan 1 verticale/horizontale asymptoot kunnen hebben? Neem de helft van een small eclips . Volgens mij heb je boven de eclips een verticale asymptoot, maar ook daaronder.

Uiteraard kunnen (grafieken van) functies meer dan één horizontale of verticale asymptoot hebben. Een eenvoudig voorbeeld is de functie

f(x) = tan x

Deze heeft (op R) zelfs oneindig veel verticale asymptoten. En vergeet niet dat je ook nog schuine asymptoten hebt.

Een eclips is een zons- of maansverduistering. Ik denk dat je hier een ellips bedoelt. Maar die heeft geen asymptoten. Een hyperbool wél, die heeft twee asymptoten die elkaar snijden in een punt dat het centrum van de hyperbool wordt genoemd.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

dinsdag 29 oktober 2013 @ 11:08:25 #71

thenxero

quote:
Op zondag 27 oktober 2013 23:31 schreef Riparius het volgende:

[..]

Als een docent van de uni dat zo opschrijft zou die persoon ontslagen mogen worden wat mij betreft.

Want hij noemt het domein van f ' niet?

dinsdag 29 oktober 2013 @ 15:14:06 #72

Riparius

quote:
Op dinsdag 29 oktober 2013 11:08 schreef thenxero het volgende:

[..]

Want hij noemt het domein van f ' niet?

Nee, ik doelde op het feit dat hij of zij 1/√(a/b) herschrijft als √b/√a. Dat geldt alleen als a > 0 en tevens b > 0, maar aan die voorwaarde is niet voldaan voor −1 < x < 0, terwijl de functie wel is gedefinieerd en differentieerbaar is op (−1, 0).

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

dinsdag 29 oktober 2013 @ 17:41:52 #73

Dale.

Vraagje... Ik wil de volgende vergelijking oplossen...

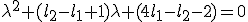
$\lambda^2 + (l_2 - l_1 + 1)\lambda + (4l_1 - l_2 - 2) = 0$

Oplossingen mogen reëel of complex zijn zolang het reëel deel maar negatief is. Met wolfram alpha krijg ik

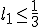
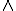
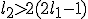$l_1 \leq \frac{1}{3}$ $\wedge$ $l_2 > 2(2l_1 - 1)$ of
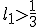
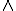
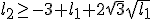
$l_1 > \frac{1}{3}$ $\wedge$ $l_2 \geq -3 + l_1 + 2\sqrt{3}\sqrt{l_1}$

Nu heb ik

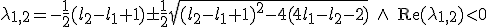
$\lambda_{1,2} = -\frac{1}{2}(l_2 - l_1 + 1) \pm \frac{1}{2} \sqrt{(l_2 - l_1 + 1)^2 - 4(4l_1 - l_2 - 2)} \ \wedge \ \mathrm{Re}(\lambda_{1,2}) < 0$

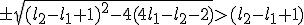
$\pm \sqrt{(l_2 - l_1 + 1)^2 - 4(4l_1 - l_2 - 2)} > (l_2 - l_1 + 1)$

Nu splits het probleem zich geloof ik op in twee problemen namelijk...

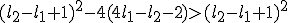
$(l_2 - l_1 + 1)^2 - 4(4l_1 - l_2 - 2) > (l_2 - l_1 + 1)^2$
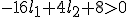
$-16l_1 + 4l_2 + 8 > 0$
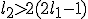
$l_2 > 2(2l_1 - 1)$

En

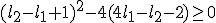$(l_2 - l_1 + 1)^2 -4(4l_1 - l_2 - 2) \geq 0$ (groter of gelijk aan nul omdat als de discriminant kleiner is dan nul dan is die complex en dan hoeven we dus alleen nog maar te zorgen dat de eerste term kleiner is dan nul)
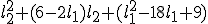
$l_2^2 + (6 - 2l_1)l_2 + (l_1^2 - 18l_1 + 9)$
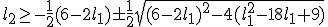
$l_2 \geq -\frac{1}{2}(6 - 2l_1) \pm \frac{1}{2}\sqrt{(6 - 2l_1)^2 - 4(l_1^2 - 18l_1 + 9)}$
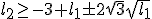
$l_2 \geq -3 + l_1 \pm 2 \sqrt{3}\sqrt{l_1}$

Nu valt de oplossing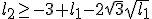 $l_2 \geq -3 + l_1 - 2 \sqrt{3}\sqrt{l_1}$ blijkbaar af, waarom is mij nie geheel duidelijk.

Vervolgens om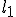 $l_1$ bound te bepalen...

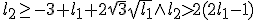$l_2 \geq -3 + l_1 + 2\sqrt{3}\sqrt{l_1} \wedge l_2 > 2(2l_1 - 1)$ dus
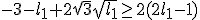
$-3 - l_1 + 2\sqrt{3}\sqrt{l_1} \geq 2(2l_1 - 1)$
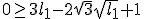
$0 \geq 3l_1 - 2\sqrt{3}\sqrt{l_1} + 1$
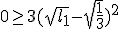
$0 \geq 3(\sqrt{l_1} - \sqrt{\frac{1}{3}})^2$
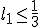
$l_1 \leq \frac{1}{3}$

Nu mijn probleem is is dat ik het niet geheel systimatisch heb opgelost en min of meer naar de oplossing van Wolfram Alpha heb gewerkt. En ik niet precies goed snap waarom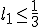 $l_1 \leq \frac{1}{3}$ bij hoort 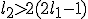$l_2 > 2(2l_1 - 1)$ en
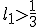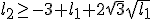
$l_1 > \frac{1}{3}$ bij $l_2 \geq -3 + l_1 + 2\sqrt{3}\sqrt{l_1}$

[ Bericht 4% gewijzigd door Dale. op 29-10-2013 19:09:10 ]

dinsdag 29 oktober 2013 @ 18:38:53 #74

Riparius

quote:
Op dinsdag 29 oktober 2013 17:41 schreef Dale. het volgende:
Vraagje... Ik wil de volgende vergelijking oplossen...

$\lambda^2 + (l_2 - l_1 + 1)\lambda + (4l_1 - l_2 - 2) < 0$

Oplossingen mogen reëel of complex zijn zolang het reëel deel maar negatief is.

Het is onduidelijk wat nu precies de bedoeling is. Als je polynoom in λ een complexe waarde heeft, dan heeft < hier geen betekenis, dus de vraagstelling klopt zo alvast niet. Het zou kunnen dat je bedoelt

$\mathrm{Re}(\lambda^2 + (l_2 - l_1 + 1)\lambda + (4l_1 - l_2 - 2)) < 0$

maar als ik dat in WolframAlpha invoer krijg ik toch iets heel anders, evenals trouwens bij invoer van je oorspronkelijke ongelijkheid.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

dinsdag 29 oktober 2013 @ 18:50:59 #75

Dale.

-edit-

Sorry beetje in de war...

Wat ik wil is dat de oplossingen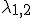 $\lambda_{1,2}$ van de kwadratische vergelijking

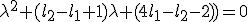
$\lambda^2 + (l_2 - l_1 + 1)\lambda + (4l_1 - l_2 - 2)) = 0$

een negatief reëel deel hebben.

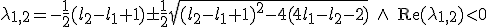
$\lambda_{1,2} = -\frac{1}{2}(l_2 - l_1 + 1) \pm \frac{1}{2} \sqrt{(l_2 - l_1 + 1)^2 - 4(4l_1 - l_2 - 2)} \ \wedge \ \mathrm{Re}(\lambda_{1,2}) < 0$

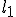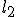
e.g. zoek ik de range van waardes 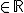$l_1$ , $l_2$ $\in \mathbb{R}$ (die wel reëel zijn) wat mij een negatief reëel deel geeft voor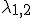 $\lambda_{1,2}$

Dus...

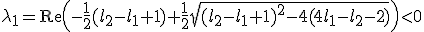
$\lambda_1 = \mathrm{Re}\left(-\frac{1}{2}(l_2 - l_1 + 1) + \frac{1}{2} \sqrt{(l_2 - l_1 + 1)^2 - 4(4l_1 - l_2 - 2)}\right) < 0$

en

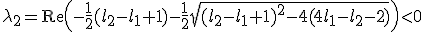
$\lambda_2 = \mathrm{Re}\left(-\frac{1}{2}(l_2 - l_1 + 1) - \frac{1}{2} \sqrt{(l_2 - l_1 + 1)^2 - 4(4l_1 - l_2 - 2)}\right) < 0$

Wolfram: eerste, tweede.

Ik geloof dat de uitwerkingen wel gedeeltelijk kloppen in de bovenstaande post. Alleen faal ik in de systematische aanpak.

[ Bericht 15% gewijzigd door Dale. op 29-10-2013 19:15:40 ]

dinsdag 29 oktober 2013 @ 19:01:11 #76

Aardappeltaart

Met slagroom

Ik ga over 'n paar weken proefstuderen in Utrecht voor de studie wiskunde (en toepassingen). Toevallig iemand hier met ervaringen over Nederlandse wiskunde studies, met name Utrecht (of Nijmegen)? Waar moet ik (niet) op letten, bij wiskunde?
In Utrecht spreekt het me wel aan dat ik veel keuzevrijheid heb en kan switchen naar wiskunde en toepassingen mocht de pure theoretische (afleidingen, historie) kant me geen voldoening geven.
(Vond deze vraag geen apart topic waard en hoop hier wat reacties te kunnen krijgen erop.)

dinsdag 29 oktober 2013 @ 19:32:58 #77

Riparius

quote:
Op dinsdag 29 oktober 2013 18:50 schreef Dale. het volgende:
-edit-

Sorry beetje in de war...

Wat ik wil is dat de oplossingen $\lambda_{1,2}$ van de kwadratische vergelijking

$\lambda^2 + (l_2 - l_1 + 1)\lambda + (4l_1 - l_2 - 2) = 0$

een negatief reëel deel hebben.

Als we aannemen dat l₁ en l₂ reëel zijn en je vierkantsvergelijking heeft twee reële wortels λ₁ en λ₂, dan zijn deze beide negatief als λ₁ + λ₂ < 0 en tevens λ₁λ₂ > 0, dus

l₂ - l₁ + 1 > 0 ∧ 4l₁ - l₂ - 2 > 0

Heeft de vierkantsvergelijking twee toegevoegd complexe wortels, dan zijn de reële delen hiervan negatief als de som λ₁ + λ₂ negatief is, dus

l₂ - l₁ + 1 > 0

Helpt dit?

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

dinsdag 29 oktober 2013 @ 20:15:07 #78

ronaldoo12

70
∑
k=10

kan iemand me helpen met wat hier uitkomt ?

dinsdag 29 oktober 2013 @ 20:20:57 #79

Riparius

quote:
Op dinsdag 29 oktober 2013 20:15 schreef ronaldoo12 het volgende:
70
∑
k=10

kan iemand me helpen met wat hier uitkomt ?

Nee, dat kan niemand, want je geeft niet aan wat er wordt gesommeerd ...

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

dinsdag 29 oktober 2013 @ 20:21:17 #80

Dale.

Het eerste stukje begrijp ik inderdaad, als l₂ - l₁ + 1 > 0 ∧ 4l₁ - l₂ - 2 > 0 dat dan inderdaad de waardes van λ kleiner zijn dan 0.

Het tweede stukje niet helemaal... Ik snap dat als er complexe wortels zijn dat als reële delen negatief zijn dat dan λ₁ + λ₂ negatief is. Alleen waarom geldt l₂ - l₁ + 1 > 0 dan?

Voor het eerste stukje krijg ik nu:

l₂ > l₁ - 1 ∧ l₂ < 2(2l₁ - 1) dus l₁ - 1 < l₂ < 2(2l₁ - 1) dus l₁ - 1 < 2(2l₁ - 1) impliceert dat l₁ > 1/3

Dus voor l₁ > 1/3 geldt dat l₂ ligt in l₁ - 1 < l₂ < 2(2l₁ - 1).

En nu moet je dus nog de case bepalen voor wanneer l₁ ≤ 1/3 wat dus is als er complexe wortels zijn?

dinsdag 29 oktober 2013 @ 20:22:40 #81

Dale.

quote:
Op dinsdag 29 oktober 2013 20:15 schreef ronaldoo12 het volgende:
70
∑
k=10

kan iemand me helpen met wat hier uitkomt ?

http://en.wikipedia.org/w(...)lynomial_expressions

dinsdag 29 oktober 2013 @ 20:25:06 #82

ronaldoo12

quote:
Op dinsdag 29 oktober 2013 20:20 schreef Riparius het volgende:

[..]

Nee, dat kan niemand, want je geeft niet aan wat er wordt gesommeerd ...

70
∑
k=10
(7k − 2)

dinsdag 29 oktober 2013 @ 20:26:14 #83

Dale.

quote:
Op dinsdag 29 oktober 2013 20:25 schreef ronaldoo12 het volgende:

[..]

70
∑
k=10
(7k − 2)

$\sum_{k=10}^{70} (7k - 2)$

bedoel je dus.

dinsdag 29 oktober 2013 @ 20:27:09 #84

ronaldoo12

quote:
Op dinsdag 29 oktober 2013 20:26 schreef Dale. het volgende:

[..]

$\sum_{k=10}^{70} (7k - 2)$

bedoel je dus.

jaa dat

dinsdag 29 oktober 2013 @ 20:28:53 #85

Dale.

quote:
Op dinsdag 29 oktober 2013 20:27 schreef ronaldoo12 het volgende:

[..]

jaa dat

$\sum_{k=10}^{70} (7k - 2) = \sum_{k=10}^{70} 7k - \sum_{k=10}^{70} 2$

Helpt dit je?

dinsdag 29 oktober 2013 @ 20:31:12 #86

ronaldoo12

quote:
Op dinsdag 29 oktober 2013 20:28 schreef Dale. het volgende:

[..]

$\sum_{k=10}^{70} (7k - 2) = \sum_{k=10}^{70} 7k - \sum_{k=10}^{70} 2$

Helpt dit je?

ja die stap had ik ook,

ik loop hier vast:

7 * 2800 - .. ?

dinsdag 29 oktober 2013 @ 20:32:06 #87

ronaldoo12

die 2800 heb ik als volgt berekend: 70/2 * (10+70)

dinsdag 29 oktober 2013 @ 20:33:15 #88

Dale.

Bij beide formules moet je nog iets doen.

dinsdag 29 oktober 2013 @ 20:39:50 #89

Riparius

quote:
Op dinsdag 29 oktober 2013 20:27 schreef ronaldoo12 het volgende:

[..]

Je hebt een rekenkundige reeks. Heeft een rekenkundige reeks n termen en is de eerste term t₁ en de laatste term t_n, dan is de som S = ½n(t₁ + t_n).

Hier heb je n = 61, t₁ = 68, t_n = 488, dus S = ½·61·(68 + 488) = 16958.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

dinsdag 29 oktober 2013 @ 20:41:55 #90

ronaldoo12

quote:
Op dinsdag 29 oktober 2013 20:33 schreef Dale. het volgende:
[ afbeelding ]

ehmm.. wordt dit dan: 70+(7k-2)-10 ? ...

dinsdag 29 oktober 2013 @ 20:42:17 #91

ronaldoo12

quote:
Op dinsdag 29 oktober 2013 20:41 schreef ronaldoo12 het volgende:

[..]

ik bedoel.. 70+1-10 .. lol

dinsdag 29 oktober 2013 @ 20:44:05 #92

ronaldoo12

quote:
Op dinsdag 29 oktober 2013 20:39 schreef Riparius het volgende:

[..]

Je hebt een rekenkundige reeks. Heeft een rekenkundige reeks n termen en is de eerste term t₁ en de laatste term t_n, dan is de som S = œn(t₁ + t_n).

Hier heb je n = 61, t₁ = 68, t_n = 488, dus S = œ·61·(68 + 488) = 16958.

hoe kom je aan t1 en tn ?

dinsdag 29 oktober 2013 @ 20:44:10 #93

Dale.

quote:
Op dinsdag 29 oktober 2013 20:42 schreef ronaldoo12 het volgende:

[..]

ik bedoel.. 70+1-10 .. lol

$\sum_{k=10}^{70} (7k - 2) = \sum_{k=10}^{70} 7k - \sum_{k=10}^{70} 2 = 7\sum_{k=10}^{70} k - 2 \sum_{k=10}^{70} 1$

quote:
Op dinsdag 29 oktober 2013 20:44 schreef ronaldoo12 het volgende:

[..]

hoe kom je aan t1 en tn ?

http://nl.wikipedia.org/wiki/Rekenkundige_rij

dinsdag 29 oktober 2013 @ 20:45:15 #94

Dale.

-

[ Bericht 99% gewijzigd door Dale. op 29-10-2013 20:45:43 ]

dinsdag 29 oktober 2013 @ 21:00:15 #95

ronaldoo12

Jaaa dankulliewel ik kom eindelijk goed uit

dinsdag 29 oktober 2013 @ 21:23:58 #96

Riparius

quote:
Op dinsdag 29 oktober 2013 20:21 schreef Dale. het volgende:
Het eerste stukje begrijp ik inderdaad, als l₂ - l₁ + 1 > 0 ∧ 4l₁ - l₂ - 2 > 0 dat dan inderdaad de waardes van λ kleiner zijn dan 0.

Het tweede stukje niet helemaal... Ik snap dat als er complexe wortels zijn dat als reële delen negatief zijn dat dan λ₁ + λ₂ negatief is. Alleen waarom geldt l₂ - l₁ + 1 > 0 dan?

Als λ₁ en λ₂ de wortels zijn van de vierkantsvergelijking

λ² + pλ + q = 0

dan geldt

λ₁ + λ₂ = −p, λ₁λ₂ = q

Zijn de wortels reëel, dan is de voorwaarde voor twee negatieve reële wortels λ₁ + λ₂ < 0 en tevens λ₁λ₂ > 0 en dus p > 0 en tevens q > 0.

Zijn de wortels λ₁ en λ₂ toegevoegd complex, dan is λ₁ = α + βi en λ₂ = α − βi waarbij α en β reëel zijn. De voorwaarde dat het reële deel α van de beide wortels negatief is, is dan equivalent met 2α = λ₁ + λ₂ = −p < 0 en dus p > 0. Merk op dat nu λ₁λ₂ = α² + β² > 0, zodat de voorwaarde λ₁λ₂ = q > 0 hier redundant is.

quote:
Voor het eerste stukje krijg ik nu:

l₂ > l₁ - 1 ∧ l₂ < 2(2l₁ - 1) dus l₁ - 1 < l₂ < 2(2l₁ - 1) dus l₁ - 1 < 2(2l₁ - 1) impliceert dat l₁ > 1/3

Dus voor l₁ > 1/3 geldt dat l₂ ligt in l₁ - 1 < l₂ < 2(2l₁ - 1).

En nu moet je dus nog de case bepalen voor wanneer l₁ ≤ 1/3 wat dus is als er complexe wortels zijn?

Je uiteindelijke voorwaarde wordt

(p > 0 ∧ q > 0 ∧ p² − 4q ≥ 0) ∨ (p > 0 ∧ p² − 4q < 0)

met p = l₂ − l₁ + 1 en q = 4l₁ − l₂ − 2

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

dinsdag 29 oktober 2013 @ 23:02:36 #97

#ANONIEM

Ik heb een vraag over Lineaire Algebra 1.

Gegeven zijn de 2x2 matrices A en B. Bewijs dat de kolommenruimte van AB bevat is in de kolommenruimte van A.

Nou, stel

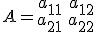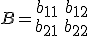
$A = \matrix{a_{11} & a_{12} \\ a_{21} & a_{22}}$ en $B = \matrix{b_{11} & b_{12} \\ b_{21} & b_{22}}$

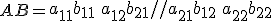
dan $AB = \matrix{{a_{11}b_{11}} & {a_{12}b_{21}} // {a_{21}b_{12}} & {a_{22}b_{22}}}$

Nou, dit laatste lukt al helemaal waardeloos. Enfin, voor de // staat de bovenste rij, na de // staat de onderste rij.

Hoe laat ik nu het gevraagde zien? De kolommenruimte van A is 1,2 of 0. Wanneer die 0 is dan zijn alle a'tjes 0, en is dus de kolommenruimte van AB ook 0, immers is AB dan de nulmatrix.

Als de kolommenruimte van A 1 is dan is er één kolom, en we zien dan in AB ook wéér een nulkolom terug.

Als de kolommenruimte van A gelijk is aan 2 ....

Maar wat als de rijenruimte van B nu eens 1 is?

Ik snap hier echt helemaal niets van.

dinsdag 29 oktober 2013 @ 23:43:02 #98

thabit

quote:
Op dinsdag 29 oktober 2013 23:02 schreef Amoeba het volgende:
Ik heb een vraag over Lineaire Algebra 1.

Gegeven zijn de 2x2 matrices A en B. Bewijs dat de kolommenruimte van AB bevat is in de kolommenruimte van A.

Nou, stel

$A = \matrix{a_{11} & a_{12} \\ a_{21} & a_{22}}$ en $B = \matrix{b_{11} & b_{12} \\ b_{21} & b_{22}}$

dan $AB = \matrix{{a_{11}b_{11}} & {a_{12}b_{21}} // {a_{21}b_{12}} & {a_{22}b_{22}}}$

Nou, dit laatste lukt al helemaal waardeloos. Enfin, voor de // staat de bovenste rij, na de // staat de onderste rij.

Hoe laat ik nu het gevraagde zien? De kolommenruimte van A is 1,2 of 0. Wanneer die 0 is dan zijn alle a'tjes 0, en is dus de kolommenruimte van AB ook 0, immers is AB dan de nulmatrix.

Als de kolommenruimte van A 1 is dan is er één kolom, en we zien dan in AB ook wéér een nulkolom terug.

Als de kolommenruimte van A gelijk is aan 2 ....

Maar wat als de rijenruimte van B nu eens 1 is?

Ik snap hier echt helemaal niets van.

LaTeX-hint:
$\left(\begin{array}{rr} a & b \\ c & d\end{array}\right)$
Wiskunde-hint: interpreteer een matrix als een lineaire afbeelding.

dinsdag 29 oktober 2013 @ 23:51:41 #99

#ANONIEM

quote:
Op dinsdag 29 oktober 2013 23:43 schreef thabit het volgende:

[..]

LaTeX-hint:
$\left(\begin{array}{rr} a & b \\ c & d\end{array}\right)$
Wiskunde-hint: interpreteer een matrix als een lineaire afbeelding.

Ik heb nog een vraag, niet over de uitwerking, maar hoe ver moet ik dit oplossen?

Gegeven is een stelsel vergelijkingen met 3 variabelen en een parameter a. De vraagstelling luidt: los het volgende stelsel vergelijkingen op voor iedere waarde van a.

Nu heb ik het geschreven als

Ax = b

En dus x = A^-1b voor iedere waarde van a waarvoor A inverteerbaar is (dus determinant ongelijk 0 ). Verder heb ik de waarden voor a bekeken waarvoor A niet inverteerbaar is.

Moet ik nu op het tentamen die inverse van A ook nog bepalen, of hoeft dat niet denk je?

[ Bericht 2% gewijzigd door #ANONIEM op 29-10-2013 23:52:52 ]

dinsdag 29 oktober 2013 @ 23:56:58 #100

thabit

De matrix A kun je zien als een afbeelding van R² naar R² die v naar Av stuurt. De kolomruimte is niets anders dan het beeld van deze afbeelding, d.w.z. alle vectoren die daadwerkelijk van de vorm Av zijn. De matrix AB is als afbeelding gelijk aan B gevolgd door A: (AB)v = A(Bv). Alles wat van geschreven kan worden als ABv kan dus ook zeker geschreven worden als Aw (nl met w = Bv). Daarom is het beeld van AB bevat in het beeld van A.

Forum Opties
Forumhop:
Hop naar:	(afkorting, bv 'KLB')

» school, studie en onderwijs

» school, studie en onderwijs