SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Ik heb een formule berekent dat gegeven een initial estimate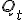 
, een aantal i.i.d. samples 
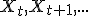en een reeks update rates 
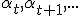een final estimate 
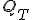maakt:
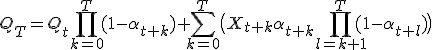
De intentie is dat het een estimate maakt voor de mean van een distributie waar de samples van afkomstig zijn.
De bias van deze estimate is simpel afgeleid, maar ik heb geen clou voor de variance. Dit komt doordat de update rate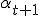
dependent is op alle vorige 
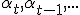en ook random variables kunnen zijn.
Iemand een suggestie hoe dit aan te pakken? Mijn reden om het algebraisch af te leiden is om verschillende invullingen van de update rates / samples leidt tot verschillende variance/biases.
// UPDATE:
Inmiddels heb ik iets weten te verzinnen. Extra detail: Qt is independent van Xt, Xt+1,... samples.
Herschrijf de bovenste equation als
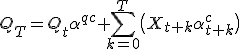
waar
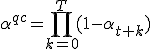, en 
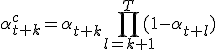
Dan heb je dus een reeks random variables die gesummed moeten worden, tenzij de update rates ook stochastic zijn. Ik kom dan op de volgende variance:
![Var(Q_T) = E[\alpha^{qc}]^2 Var(Q_t) + E[Q_t]^2 Var(\alpha^{qc}) + Var(\alpha^{qc})Var(Q_t)](https://forum.fok.nl/lib/mimetex.cgi?Var%28Q_T%29%20%3D%20E%5B%5Calpha%5E%7Bqc%7D%5D%5E2%20Var%28Q_t%29%20%2B%20E%5BQ_t%5D%5E2%20Var%28%5Calpha%5E%7Bqc%7D%29%20%2B%20Var%28%5Calpha%5E%7Bqc%7D%29Var%28Q_t%29%20)
![+ \sum_{k=0}^T \bigl( E[\alpha_{t+k}^{c}]^2 Var(X_{t+k}) + E[X_{t+k}]^2 Var(\alpha_{t+k}^{c}) + Var(\alpha_{t+k}^{c}) Var(X_{t+k}) \bigr)](https://forum.fok.nl/lib/mimetex.cgi?%2B%20%5Csum_%7Bk%3D0%7D%5ET%20%5Cbigl%28%20E%5B%5Calpha_%7Bt%2Bk%7D%5E%7Bc%7D%5D%5E2%20Var%28X_%7Bt%2Bk%7D%29%20%2B%20E%5BX_%7Bt%2Bk%7D%5D%5E2%20Var%28%5Calpha_%7Bt%2Bk%7D%5E%7Bc%7D%29%20%2B%20Var%28%5Calpha_%7Bt%2Bk%7D%5E%7Bc%7D%29%20Var%28X_%7Bt%2Bk%7D%29%20%5Cbigr%29)
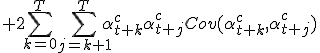
Kan iemand hier een blik op werpen en zeggen of dit misschien klopt?
[ Bericht 10% gewijzigd door koffiegast op 22-10-2013 15:27:40 ]
De intentie is dat het een estimate maakt voor de mean van een distributie waar de samples van afkomstig zijn.
De bias van deze estimate is simpel afgeleid, maar ik heb geen clou voor de variance. Dit komt doordat de update rate
Iemand een suggestie hoe dit aan te pakken? Mijn reden om het algebraisch af te leiden is om verschillende invullingen van de update rates / samples leidt tot verschillende variance/biases.
// UPDATE:
Inmiddels heb ik iets weten te verzinnen. Extra detail: Qt is independent van Xt, Xt+1,... samples.
Herschrijf de bovenste equation als
waar
Dan heb je dus een reeks random variables die gesummed moeten worden, tenzij de update rates ook stochastic zijn. Ik kom dan op de volgende variance:
Kan iemand hier een blik op werpen en zeggen of dit misschien klopt?
[ Bericht 10% gewijzigd door koffiegast op 22-10-2013 15:27:40 ]
Ik heb een vraag over directional derivatives.
Gevraagd wordt: op welk punt op de paraboloïde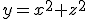
is het raakvlak parallel aan het vlak 
.
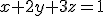Het raakvlak van de paraboloïde is dan dus:
.
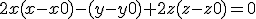Hoe moet ik nu verder gaan?
Gevraagd wordt: op welk punt op de paraboloïde
Het raakvlak van de paraboloïde is dan dus:
Hoe moet ik nu verder gaan?
“I'm not about caring; I'm about winning.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
Herschrijf de vergelijking van je paraboloïde in de gedaantequote:Op dinsdag 22 oktober 2013 16:41 schreef PowerData het volgende:
Ik heb een vraag over directional derivatives.
Gevraagd wordt: op welk punt op de paraboloïde
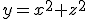
is het raakvlak parallel aan het vlak
Het raakvlak van de paraboloïde is dan dus:.
Hoe moet ik nu verder gaan?
F(x, y, z) = 0
Een normaalvector in een punt (x0,y0,z0) op dit vlak is nu
(∂F/∂x(x0,y0,z0), ∂F/∂y(x0,y0,z0), ∂F/∂z(x0,y0,z0)) = (2x0, −1, 2z0)
en deze vector moet dezelfde richting hebben als de normaalvector (1, 2, 3) van je vlak x + 2y + 3z = 1. Nu moet je het toch echt wel op kunnen lossen. Zie ook hier.
[ Bericht 2% gewijzigd door Riparius op 22-10-2013 17:46:19 ]
Bedankt voor je antwoord.quote:
[..]
Herschrijf de vergelijking van je paraboloïde in de gedaante
F(x,y,z) = 0
Een normaalvector in een punt (x0,y0,z0) op dit vlak is nu
(∂F/∂x(x0,y0,z0), ∂F/∂y(x0,y0,z0), ∂F/∂z(x0,y0,z0))
en deze vector moet dezelfde richting hebben als de normaalvector (1, 2, 3) van je vlak x + 2y + 3z = 1. Nu moet je het toch echt wel op kunnen lossen.
Dan krijg je dus:
normaalvector =
Dan bestaat er toch geen oplossing? Gezien welke waarden er ook worden gekozen, er geldt nooit , (2x0, -1, z0) = (1, 2, 3).
“I'm not about caring; I'm about winning.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
Om te beginnen: gebruik ook subscript als je TeX gebruikt. Verder: zie mijn post hierboven voor de correcte vergelijking van het raakvlak.quote:
[..]
Bedankt voor je antwoord.
Dan krijg je dus:
normaalvector =
Dan bestaat er toch geen oplossing? Gezien welke waarden er ook worden gekozen, er geldt nooit (2x0, -1, 2z0) = (1, 2, 3).
Je vergist je als je meent dat er geen oplossing is. De normaalvectoren moeten in elkaars verlengde liggen, ze hoeven niet hetzelfde te zijn.
Oké, dan zal ik het maal een constante doen (c).quote:
[..]
Om te beginnen: gebruik ook subscript als je TeX gebruikt. Verder: zie mijn post hierboven voor de correcte vergelijking van het raakvlak.
Je vergist je als je meent dat er geen oplossing is. De normaalvectoren moeten in elkaars verlengde liggen, ze hoeven niet hetzelfde te zijn.
c(2x0, -1, 2z0) = (1, 2, 3)
c = 2 / -1 = -2.
dus:
-4x0 = 1
=> x0 = -1/4
-4z0 = 3
=> z0 = -3/4
dus het raakvlak van F(x) = 0 is parallel aan de vergelijking x + 2y + 3z = 1 in het punt P(-1/4, y0, -3/4), waarin y0 nog alles kan zijn. Correct?
“I'm not about caring; I'm about winning.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
Nee, fout.quote:
[..]
Oké, dan zal ik het maal een constante doen (c).
c(2x0, -1, 2z0) = (1, 2, 3)
c = 2 / -1 = -2.
dus:
-4x0 = 1
=> x0 = -1/4
-4z0 = 3
=> z0 = -3/4
dus het raakvlak van F(x,y,z) = 0 is parallel aan het vlak met de vergelijking x + 2y + 3z = 1 in het punt P(-1/4, y0, -3/4), waarin y0 nog alles kan zijn. Correct?
Je gebruikt nu zomaar opeens y0 in plaats van z0.
Verder moet je nu y0 nog bepalen.
[ Bericht 2% gewijzigd door Riparius op 22-10-2013 18:12:37 ]
Excuus, ik heb het inmiddels verbeterd. Wat is verder mijn denkfout?quote:
[..]
Nee, fout.
Je gebruikt nu zomaar opeens y0 in plaats van z0.
“I'm not about caring; I'm about winning.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
Het is zo goed, maar nu moet je y0 nog bepalen.quote:
[..]
Excuus, ik heb het inmiddels verbeterd. Wat is verder mijn denkfout?
Oké.
y0 = x02 + z02 = (-1/4)2 + (-3/4)2 = 1/16 + 9/16 = 10/16 = 5/8.
Dus P(1/4, 5/8, 3/4).
y0 = x02 + z02 = (-1/4)2 + (-3/4)2 = 1/16 + 9/16 = 10/16 = 5/8.
Dus P(1/4, 5/8, 3/4).
“I'm not about caring; I'm about winning.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
Dat is het, behalve dat je nu weer je mintekens vergeet. Je moet echt netter gaan werken.quote:
Oké.
y0 = x02 + z02 = (-1/4)2 + (-3/4)2 = 1/16 + 9/16 = 10/16 = 5/8.
Dus P(−1/4, 5/8, −3/4).
Ik denk het wel, ik moest vooral even zien dat je met normaalvectoren moest werken.quote:
Je kunt dus stellen dat de vraag: 'wanneer is het raakvlak van F(x) parallel aan g(x) = c?' equivalent is aan de vraag: 'wanneer ligt de normaalvector van F(x) in het verlengde van de normaalvector van g(x) = c?'?
“I'm not about caring; I'm about winning.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
- Harvey Specter
“Take a step back, look at the bigger picture.”
Als je met g(x,y,z) = c een vergelijking van een plat vlak bedoelt, dan klopt dit. Twee vlakken die parallel zijn hebben immers ook normaalvectoren die parallel zijn. En: netter werken, je maakt voortdurend fouten met je notatie.quote:
[..]
Ik denk het wel, ik moest vooral even zien dat je met normaalvectoren moest werken.
Je kunt dus stellen dat de vraag: 'wanneer is het raakvlak aan F(x,y,z) = 0 parallel aan het vlak g(x,y,z) = c?' equivalent is aan de vraag: 'wanneer ligt de normaalvector van F(x,y,z) = 0 in het verlengde van de normaalvector van g(x,y,z) = c?'?
[ Bericht 4% gewijzigd door Riparius op 22-10-2013 18:34:01 ]
Ik heb een vraag over een vraagstuk waar ik eigenlijk nog niet klaar voor ben, maar ik wil een poging wagen. Gonio is een zwakke kant van mij, maar dat wil ik versterken.
Komt die: http://www2.cito.nl/vo/ex2013/VW-1025-a-13-1-o.pdf
Vraag 6 ( Toon uitgaande van de gelijkvormigheid van de driehoeken GCR en GPQ aan dat deze formule juist is.)
Ik stel dat:
alfa1= hoek dat gemaakt wordt door de sinus alfa1 = CR/CG
alfa2= hoek dat gemaakt wordt door sinus alfa2 = PQ/GP
CR = sin alfa 1
GP^2 = GQ^2 + PQ^2 = (cosalfa2)^2 + (sinalfa2)^2
en dus GP= cosalfa2 + sinalfa2
CG^2=GR^2 + CR^2 = (cosalfa1)^2 + (sinalfa1)^2
en dus CG=cosalfa1 + sinalfa1
Ik stel ook dat:
CR/CG=PQ/GP
Opdat:
PQ=(CR*GP)/CG
Opdat:
PQ=(sinalfa1 * cosalfa2 + sinalfa2)/(sinalfa1+cosalfa1)
Hierna loop ik vast....
Ik heb het geprobeerd zo netjes/begrijpbaar mogelijk neer te zetten.
Komt die: http://www2.cito.nl/vo/ex2013/VW-1025-a-13-1-o.pdf
Vraag 6 ( Toon uitgaande van de gelijkvormigheid van de driehoeken GCR en GPQ aan dat deze formule juist is.)
Ik stel dat:
alfa1= hoek dat gemaakt wordt door de sinus alfa1 = CR/CG
alfa2= hoek dat gemaakt wordt door sinus alfa2 = PQ/GP
CR = sin alfa 1
GP^2 = GQ^2 + PQ^2 = (cosalfa2)^2 + (sinalfa2)^2
en dus GP= cosalfa2 + sinalfa2
CG^2=GR^2 + CR^2 = (cosalfa1)^2 + (sinalfa1)^2
en dus CG=cosalfa1 + sinalfa1
Ik stel ook dat:
CR/CG=PQ/GP
Opdat:
PQ=(CR*GP)/CG
Opdat:
PQ=(sinalfa1 * cosalfa2 + sinalfa2)/(sinalfa1+cosalfa1)
Hierna loop ik vast....
Ik heb het geprobeerd zo netjes/begrijpbaar mogelijk neer te zetten.
-
[ Bericht 62% gewijzigd door Amoeba op 22-10-2013 19:53:22 ]
[ Bericht 62% gewijzigd door Amoeba op 22-10-2013 19:53:22 ]
Fervent tegenstander van het korps lasergamers.
Als eerste een tip, maak het jezelf en zeker anderen niet te moeilijk door een alfa1 en alfa2 te definieren wanneer er al een alfa in het probleem gebruikt wordt. gebruik dan een theta, of phi, of beta ofzo. Of maak er A en B van, dit is ook korter en dus duidelijker. Je zou ook tex-commando's kunnen gebruiken, maar aangezien je het eindexamen VWO aan het maken bent, heb je dit nog nooit gedaan waarschijnlijkquote:
Ik heb een vraag over een vraagstuk waar ik eigenlijk nog niet klaar voor ben, maar ik wil een poging wagen. Gonio is een zwakke kant van mij, maar dat wil ik versterken.
Komt die: http://www2.cito.nl/vo/ex2013/VW-1025-a-13-1-o.pdf
Vraag 6 ( Toon uitgaande van de gelijkvormigheid van de driehoeken GCR en GPQ aan dat deze formule juist is.)
Ik stel dat:
alfa1= hoek dat gemaakt wordt door de sinus alfa1 = CR/CG
alfa2= hoek dat gemaakt wordt door sinus alfa2 = PQ/GP
Naast een aantal elementaire fouten (quote:CR = sin alfa 1
GP^2 = GQ^2 + PQ^2 = (cosalfa2)^2 + (sinalfa2)^2
en dus GP= cosalfa2 + sinalfa2
CG^2=GR^2 + CR^2 = (cosalfa1)^2 + (sinalfa1)^2
en dus CG=cosalfa1 + sinalfa1
Ik stel ook dat:
CR/CG=PQ/GP
Opdat:
PQ=(CR*GP)/CG
Opdat:
PQ=(sinalfa1 * cosalfa2 + sinalfa2)/(sinalfa1+cosalfa1)
Hierna loop ik vast....
Ik heb het geprobeerd zo netjes/begrijpbaar mogelijk neer te zetten.
Je hebt die nieuwe hoeken namelijk helemaal niet nodig als je gelijkvormigheid goed gebruikt. Van een aantal punten is namelijk de (x,y) coordinaat gegeven. Als je die slim gebruikt moet je er ook uit kunnen komen.
Het eerste wat eruit springt:quote:
GP^2 = GQ^2 + PQ^2 = (cosalfa2)^2 + (sinalfa2)^2
en dus GP= cosalfa2 + sinalfa2
Als A2 + B2 = C2 (ongelijk aan 0) dan geldt niet dat C = A + B. Dat weet je hopelijk?
Heb deze vraag recent nog gemaakt. De kern zit hem erin dat je inderdaad de zijdes die overeenkomen door elkaar deelt. De zijdes zijn uit te drukken in een combinatie van de termen sin(alfa), cosinus(alfa) en 1. Kijk goed naar de vierkanten en de zijdes die bij de aangegeven hoeken alfa horen. Een aantal punten komen qua x of y coördinaat met elkaar overeen, bijvoorbeeld:
CR = YC - YR (zie plaatje)
YC = YT = ET = BE + BT= Sin(alfa)+ Cos(alfa) (Zie plaatje; gebruik het verband tussen een hoek alfa en de bijbehorende x en y coördinaat).
Overigens, hoever ben je dan al met je wiskunde? Je zegt dat je er niet aan toe bent.
Handig lijkt me:
- Meetkundige bewijzen / gelijkvormigheid;
- Goniometrische identiteiten;
- Poolcoördinaten: (verband tussen (straal, hoek) en (x,y) lijkt me 't overzicht voor je vereenvoudigen).
[ Bericht 1% gewijzigd door Aardappeltaart op 22-10-2013 20:00:40 ]
Volgens mij haal je hier de X en Y coordinaat door elkaarquote:
[..]
Het eerste wat eruit springt:
Als A2 + B2 = C2 dan geldt niet dat C = A + B. Dat weet je hopelijk?
Heb deze vraag recent nog gemaakt. De kern zit hem erin dat je inderdaad de zijdes die overeenkomen door elkaar deelt. De zijdes zijn uit te drukken in een combinatie van de termen sin(alfa), cosinus(alfa) en 1. Kijk goed naar de vierkanten en de zijdes die bij de aangegeven hoeken alfa horen. Een aantal punten komen qua x of y coördinaat met elkaar overeen, bijvoorbeeld:
CR = XC - XR (zie plaatje)
XC = XT = BE + TB = Sin(alfa)+ Cos(alfa) (Zie plaatje; gebruik het verband tussen een hoek alfa en de bijbehorende x en y coördinaat).
Overigens, hoever ben je dan al met je wiskunde? Je zegt dat je er niet aan toe bent.
Handig lijkt me:
- Meetkundige bewijzen / gelijkvormigheid;
- Goniometrische identiteiten;
- Poolcoördinaten: (verband tussen (straal, hoek) en (x,y) lijkt me 't overzicht voor je vereenvoudigen).
Bedankt. Ik heb het verbeterd. Het erge is, is dat dit soort haastige slordigheidsfouten weleens voorkomen in mijn toetsen. Daardoor zelden een 10.quote:
[..]
Volgens mij haal je hier de X en Y coordinaat door elkaar
Dank u veel beide. Ik dacht dat schuine zijde = verticale zijde + horizontale zijde, maar het is dus horizontale zijde = schijne zijde + verticale zijde. Stom van me.
Mijn voorkennis is wiskunde a, vwo, maar ik ben het nu stap voor stap aan het uitbreiden tot wiskunde b. Tot zover laatst nog met mijn prive wiskunde docent gehad over de eenheidscirkel, waar de sinus/cosinus zit , de cosinus/sinusregel de sinus functie en cosinus functie. Met dat laatste dus de amplitude/periode/evenwichtslijn/translaties/beginpunten.
Ik ga jullie uitleg nog even doorlezen en weer naar het vraagstuk kijken. Hoop dat ik hem dan wel zie, zoniet, dan zal ik hier weer posten met wat ik gedaan heb/waar ik vast zit.
Mijn voorkennis is wiskunde a, vwo, maar ik ben het nu stap voor stap aan het uitbreiden tot wiskunde b. Tot zover laatst nog met mijn prive wiskunde docent gehad over de eenheidscirkel, waar de sinus/cosinus zit , de cosinus/sinusregel de sinus functie en cosinus functie. Met dat laatste dus de amplitude/periode/evenwichtslijn/translaties/beginpunten.
Ik ga jullie uitleg nog even doorlezen en weer naar het vraagstuk kijken. Hoop dat ik hem dan wel zie, zoniet, dan zal ik hier weer posten met wat ik gedaan heb/waar ik vast zit.
Ik heb alleen nog niet gevonden waarom CR = cosα + sinα - 1
Verder is heel de opgave me eigenlijk wel gelukt.
Verder is heel de opgave me eigenlijk wel gelukt.
Fervent tegenstander van het korps lasergamers.
OF = sinα + cosα + 1
Lijkt me vrij helder.
∠GCR = π/2-α
DR' = QR = sin(π/2-α) = cos(α)
En dus
RH = sin(α)
En inderdaad
PQ = OF/GR * CR
GR = RH + GH = sin(α) + 1
En dan alleen CR nog ..
Lijkt me vrij helder.
∠GCR = π/2-α
DR' = QR = sin(π/2-α) = cos(α)
En dus
RH = sin(α)
En inderdaad
PQ = OF/GR * CR
GR = RH + GH = sin(α) + 1
En dan alleen CR nog ..
Fervent tegenstander van het korps lasergamers.
TE kan je uitdrukken in Sin(alfa)+Cos(alfa), zie mijn eerdere reply.quote:Op dinsdag 22 oktober 2013 20:30 schreef Amoeba het volgende:
Ik heb alleen nog niet gevonden waarom CR = cosα + sinα - 1
Verder is heel de opgave me eigenlijk wel gelukt.
CR = TE - GF
GF = 1, dat is gegeven
Vergelijk de y-coordinaat van G eens met die van Cquote:
OF = sinα + cosα + 1
Lijkt me vrij helder.
∠GCR = π/2-α
DR' = QR = sin(π/2-α) = cos(α)
En dus
RH = sin(α)
En inderdaad
PQ = OF/GR * CR
GR = RH + GH = sin(α) + 1
En dan alleen CR nog ..
Hoi, ik heb weer een (waarschijnlijk niet al te snuggere) vraag.
Ik snap precies wat ze hier doen bij het oplossen van deze opgave, ik had echter een andere manier in mijn gedachte.
Ik zou beide grondtallen met 3 vermenigvuldigen zodat je vervolgens 3 (links) en 27 (rechts) als grondtal krijgt. Vervolgens wordt de uitdrukking rechts 3^((3)(14x-11)) en links gewoon 3^(x^(2)+27x-64).
Je komt wanneer je dit doet echter niet goed uit. Waar ga ik de fout in?
Alvast bedankt
Ik snap precies wat ze hier doen bij het oplossen van deze opgave, ik had echter een andere manier in mijn gedachte.
Ik zou beide grondtallen met 3 vermenigvuldigen zodat je vervolgens 3 (links) en 27 (rechts) als grondtal krijgt. Vervolgens wordt de uitdrukking rechts 3^((3)(14x-11)) en links gewoon 3^(x^(2)+27x-64).
Je komt wanneer je dit doet echter niet goed uit. Waar ga ik de fout in?
Alvast bedankt
