SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Het kan korter, bedenk ik me net. Je hebt namelijk:quote:Op dinsdag 25 september 2012 19:40 schreef dynamiet het volgende:
[..]
Heel erg bedankt! Hier heb ik wat aan
(1) Σ n∙xn = x∙Σ n∙xn-1
Welnu, we weten dat :
(2) Σ xn = 1/(1-x) (|x| < 1)
Beide leden van (2) differentiëren naar x geeft:
(3) Σ n∙xn-1 = 1/(1-x)2 (|x| < 1)
En beide leden van (3) met x vermenigvuldigen levert dus:
(4) Σ n∙xn = x/(1-x)2 (|x| < 1)
Substitutie van x = 1/3 in (4) geeft dan:
(5) Σ n∙(1/3)n = (1/3)/(2/3)2 = (1/3)∙(9/4) = 3/4
ΟΕΔ
[ Bericht 0% gewijzigd door Riparius op 27-09-2012 21:21:21 ]
iemand hier die wolfram alpha app gekocht heeft?
Is het het geld waard?
(link voor android, hij is er ook voor iOS: klik )
Is het het geld waard?
(link voor android, hij is er ook voor iOS: klik )
Winnaar KLB verkiezingen 2012.
Ik heb hem niet maar gezien de ratings is het geen miskoop. Sowieso is het maar ¤3,17. Als je de gewone wolfram alpha fijn vindt, dan zal je dat ook wel waarderen. Denk alleen dat het niet heel erg veel toevoegt t.o.v. de gewone site.quote:Op woensdag 26 september 2012 20:00 schreef gogosweden het volgende:
iemand hier die wolfram alpha app gekocht heeft?
Is het het geld waard?
(link voor android, hij is er ook voor iOS: klik )
ik zit er een beetje over in dat het met een mobiel toetsenbord natuurlijk veel kutter werken is.quote:
[..]
Ik heb hem niet maar gezien de ratings is het geen miskoop. Sowieso is het maar ¤3,17. Als je de gewone wolfram alpha fijn vindt, dan zal je dat ook wel waarderen. Denk alleen dat het niet heel erg veel toevoegt t.o.v. de gewone site.
Winnaar KLB verkiezingen 2012.
Ik moet de sample mean en covariance uitrekenen van een variabele (vector)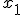 
conditioneel op twee variabelen (vectoren) 
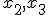met MATLAB. Er is niet genoeg bewijs om aan te nemen dat de variabelen individueel of gezamenlijk normaal verdeeld zijn. Hoe werkt dat (formule/idee, MATLAB code tikken lukt zelf nog wel)?
[ Bericht 2% gewijzigd door Physics op 27-09-2012 10:22:55 ]
[ Bericht 2% gewijzigd door Physics op 27-09-2012 10:22:55 ]
Ik heb 'm gepiraat. Geen slechte app, maar de site is beter.quote:
iemand hier die wolfram alpha app gekocht heeft?
Is het het geld waard?
(link voor android, hij is er ook voor iOS: klik )
hmm even kijken wat ik zal doen dan.quote:Op donderdag 27 september 2012 07:11 schreef Amoeba het volgende:
[..]
Ik heb 'm gepiraat. Geen slechte app, maar de site is beter.
Winnaar KLB verkiezingen 2012.
Zonder parametrisch model wordt dat lastig. Of x2/x3 moeten discreet zijn en je voor elke combinatie (x2,x3) veel waarnemingen x1 hebt.quote:
Ik moet de sample mean en covariance uitrekenen van een variabele (vector) stochastische vector
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Nee ik heb een 24x3 data matrix, dus voor elk paar (x2,x3) heb ik één x1.quote:
[..]
Zonder parametrisch model wordt dat lastig. Of x2/x3 moeten discreet zijn en je voor elke combinatie (x2,x3) veel waarnemingen x1 hebt.
Oh, de stochasten zijn niet vectorwaardig. Dan vraag ik me af over wat voor covariantie je het hebt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Het blijkt nogal een vage vraag te zijn. Uit q-q plots en chi-squared plots is er geen bewijs voor normaliteit, integendeel. En dan in de laatste vraag moeten we opeens de assumptie doen (staat niet bij de opgave) dat de data multivariaat normaal verdeeld is.
Hoe bedoel je dat de stochasten niet vectorwaardig zijn?
Hoe bedoel je dat de stochasten niet vectorwaardig zijn?
Je stochast is univariaat, en je vector bestaat uit waarnemingen.quote:
Hoe bedoel je dat de stochasten niet vectorwaardig zijn?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dat klopt, en hoezo zou er dan geen covariantie kunnen zijn tussen de stochasten?quote:
[..]
Je stochast is univariaat, en je vector bestaat uit waarnemingen.
Je had het over "gegeven x_2, x_3", en dan is de covariantie 0 want dan zijn x_2 en x_3 constanten.quote:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Weet iemand een goed boek over functionaalanalyse?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Ik heb een vraag over verzamelingenleer en dan in het bijzonder over relaties tussen verzamelingen:
Wanneer is er nou sprake van een transitieve relatie? En geldt deze relatie ook voor een relatie met daarin slechts één element. Wat ik begrepen heb is dat voor een transitieve relatie altijd geldt:<a, b>, <b, c> en dus <c, a>, maar iemand merkte op dat een enkele element (dus bijvoorbeeld <a, b>) ook transitief is.
Wanneer is er nou sprake van een transitieve relatie? En geldt deze relatie ook voor een relatie met daarin slechts één element. Wat ik begrepen heb is dat voor een transitieve relatie altijd geldt:<a, b>, <b, c> en dus <c, a>, maar iemand merkte op dat een enkele element (dus bijvoorbeeld <a, b>) ook transitief is.
Kom maar konijntje, doe maar wiebelen wiebelen...
Misschien moet je de vraag opnieuw stellen zodra je weer nuchter bent, want hier is geen chocola van te maken.quote:
Ik heb een vraag over verzamelingenleer en dan in het bijzonder over relaties tussen verzamelingen:
Wanneer is er nou sprake van een transitieve relatie? En geldt deze relatie ook voor een relatie met daarin slechts één element. Wat ik begrepen heb is dat voor een transitieve relatie altijd geldt:<a, b>, <b, c> en dus <c, a>, maar iemand merkte op dat een enkele element (dus bijvoorbeeld <a, b>) ook transitief is.
Mijn vraag is: wanneer is er sprake van transitiviteit? En hoe zit het met een relatie R als er maar één relatie in zit, dus {<a, b>}. Want ik heb begrepen dat bij transitiviteit een driehoeksrelatie speelt, maar dat is blijkbaar niet het enige.quote:
[..]
Misschien moet je de vraag opnieuw stellen zodra je weer nuchter bent, want hier is geen chocola van te maken.
Kom maar konijntje, doe maar wiebelen wiebelen...
Je vraag blijft vaag. Transitiviteit heb je als aRb en bRc impliceert aRc voor alle elementen a,b,c, waarbij R een relatie is.
Wat is een driehoeksrelatie? Behalve dan drie mensen die een relatie met elkaar hebben. Wat bedoel je met dat er één element in een relatie zit?
Geef anders eens een voorbeeld.
Wat is een driehoeksrelatie? Behalve dan drie mensen die een relatie met elkaar hebben. Wat bedoel je met dat er één element in een relatie zit?
Geef anders eens een voorbeeld.
In de voorwaarde "als aRb en bRc, dan ook aRc" hoeven a, b, en c niet verschillend te zijn. Is dat wat je met je vraag bedoelt?
Als er één element in je verzameling zit, en dat element heeft een relatie met zichzelf, dan is er sprake van transitiviteit. Want aRb, bRc, aRc worden dan allemaal aRa. En uiteraard:
aRa en aRa ==> aRa.
aRa en aRa ==> aRa.
Maar als er nou alleen aRb in een relatie zit, dan is er geen sprake van transitiviteit? (Misschien heb ik het niet helemaal goed begrepen hoor.)quote:
Als er één element in je verzameling zit, en dat element heeft een relatie met zichzelf, dan is er sprake van transitiviteit. Want aRb, bRc, aRc worden dan allemaal aRa. En uiteraard:
aRa en aRa ==> aRa.
Misschien maak ik trouwens een denkfout... Is het zo dan een relatie per definitie op alle elementen in een verzameling slaat? Dus niet dat het slechts enkele elementen heeft?
Kom maar konijntje, doe maar wiebelen wiebelen...
Een relatie slaat op elk paar elementen van de verzameling, en voor elk paar kan de relatie wel of niet gelden. Simpel voorbeeld: neem de verzameling van reële getallen, met als relatie "<" (a is kleiner dan b). Voor elk paar getallen a en b kun je zeggen of a<b wel of niet geldt, zo geldt 1<2 wel, maar 4<3 geldt niet, etc.
Precies. Dus "aRb zit in een relatie" is nogal vaag. Je zegt ook niet: 1<2 zit in een relatie.
Misschien bedoel je dat de relatie aRb slechts voor twee verschillende elementen a en b geldt. Bijvoorbeeld:
Stel je hebt de verzameling X={1,2} en als relatie R heb je <. Dan geldt dus alleen 1<2 (niet 1<1, 2<1, 2<2). Als je wil checken op transitiviteit (dus: a<b en b<c ==> a<c), dan zie je dat je de premisse van de implicatie niet waar kan maken.
Een regel uit de logica is dat "A==>B" waar is als A niet waar is. Dus inderdaad heb je in dit voorbeeld transitiviteit. (en dit verhaal kan je ook weer algemeen maken)
Is dat wat je bedoelt?
[ Bericht 37% gewijzigd door thenxero op 29-09-2012 16:03:24 ]
Misschien bedoel je dat de relatie aRb slechts voor twee verschillende elementen a en b geldt. Bijvoorbeeld:
Stel je hebt de verzameling X={1,2} en als relatie R heb je <. Dan geldt dus alleen 1<2 (niet 1<1, 2<1, 2<2). Als je wil checken op transitiviteit (dus: a<b en b<c ==> a<c), dan zie je dat je de premisse van de implicatie niet waar kan maken.
Een regel uit de logica is dat "A==>B" waar is als A niet waar is. Dus inderdaad heb je in dit voorbeeld transitiviteit. (en dit verhaal kan je ook weer algemeen maken)
Is dat wat je bedoelt?
[ Bericht 37% gewijzigd door thenxero op 29-09-2012 16:03:24 ]
Stond hier gister niet een puzzel met 4 van die sterretjes erin? Repost? :p I like puzzles.
Blues ain't nothing but a good man feeling bad...
Daar stond de puzzel, maar hij is inmiddels weggehaald: [Bèta overig] Huiswerk- en vragentopicquote:
Stond hier gister niet een puzzel met 4 van die sterretjes erin? Repost? :p I like puzzles.
Volgens mij was het een 8*8 raster met 4 sterretjes op de diagonaal van linksboven naar rechtsonder. Ik meen dat de opdracht was om het raster in vier gelijkvormige delen op te delen, zodanig dat in elk deel een ster voorkwam en alle delen elkaar raakten.
Voor iedereen die er belang in stelt: ik heb mijn post met het elementaire bewijs met vectoren van de somformules voor cos(α + β) en sin(α + β) bewerkt tot een PDF die hier is te bekijken en desgewenst is te downloaden. Met dank aan Amoeba voor het vervaardigen van het plaatje.
Kan iemand mij misschien helpen met het volgende?
Schrijf als een exponentiele functie met grondtel e de groei van ¤3000 tegen 5% rente per jaar.
Nu is de groei dus y = 3000 * 1,05x
Maar het grondgetal moet e zijn, hoe krijg ik dat ingodsnaam voor elkaar
Schrijf als een exponentiele functie met grondtel e de groei van ¤3000 tegen 5% rente per jaar.
Nu is de groei dus y = 3000 * 1,05x
Maar het grondgetal moet e zijn, hoe krijg ik dat ingodsnaam voor elkaar
Als je dus bedenkt dat ep gelijk is aan je functie, waarbij p een uitdrukking is in x. Lukt het dan?
En bedenk dat:
3000 = eln(3000)
The way to go.
[ Bericht 45% gewijzigd door #ANONIEM op 02-10-2012 19:13:11 ]
En bedenk dat:
3000 = eln(3000)
The way to go.
[ Bericht 45% gewijzigd door #ANONIEM op 02-10-2012 19:13:11 ]
Waarom had ik die ep nodig?
Ik heb nu dit
y = 3000 * 1,05x
ep = eln3000 * eln1,05x
y = eln3000 + ln(1,05x)
y = eln(3150x)
Ik heb nu dit
y = 3000 * 1,05x
ep = eln3000 * eln1,05x
y = eln3000 + ln(1,05x)
y = eln(3150x)
Je tweede regel is in feite niet goed. Het is niet ln(1.05x)
Je moet begrijpen dat je in feite een uitdrukking krijgt waarbij e het grondtal is, en waarbij p een uitdrukking is in x. Als je e tot de macht p verheft krijg je dus in feite y.
Je wilt y omschrijven naar een vorm ep
[ Bericht 68% gewijzigd door #ANONIEM op 02-10-2012 19:29:06 ]
Je moet begrijpen dat je in feite een uitdrukking krijgt waarbij e het grondtal is, en waarbij p een uitdrukking is in x. Als je e tot de macht p verheft krijg je dus in feite y.
Je wilt y omschrijven naar een vorm ep
[ Bericht 68% gewijzigd door #ANONIEM op 02-10-2012 19:29:06 ]
e ln (1,05)x = eln1,05x toch?quote:
Je tweede regel is in feite niet goed. Het is niet ln(1.05x)
Je hebt uiteraard:quote:
Kan iemand mij misschien helpen met het volgende?
Schrijf als een exponentiele functie met grondtel e de groei van ¤3000 tegen 5% rente per jaar.
Nu is de groei dus y = 3000 * 1,05x
Maar het grondgetal moet e zijn, hoe krijg ik dat ingodsnaam voor elkaar
1,05 = eln(1,05)
Verder kun je gebruik maken van de rekenregel:
(ap)q = apq
Wat krijg je dan?
Je zou ook nog kunnen zeggen dat
3000 = eln(3000)
Dan kun je daarna nog gebruik maken van de rekenregel:
ap∙aq = ap+q
Wat krijg je dan?
Correct. (als ik me niet vergisquote:
[..]
Ohja, dat maakt dus
y = e ln(3150) * x ?
)[ Bericht 1% gewijzigd door #ANONIEM op 02-10-2012 20:09:07 ]
Nee.quote:
[..]
Ohja, dat maakt dus
y = e ln(3150) * x ?
Jawel. Bij (eln(1.05))x = eln(1.05)xquote:
Dan is de regel (ap)q = apq toch niet gebruikt?
[ Bericht 3% gewijzigd door #ANONIEM op 02-10-2012 19:48:07 ]
Daar gebruik je toch log(ab) = b*log(a) ?quote:
[..]
Jawel. Bij e^ln(1.05)^x = e^ln(1.05)x
Nee.quote:
[..]
Daar gebruik je toch log(ab) = b*log(a) ?
Ik zal je maar even uit je lijden verlossen, want dit wordt een gebed zonder end. Ik verbaas me iedere dag meer over het volstrekte gebrek aan basale wiskundekennis bij mensen die vervolgopleidingen gaan doen waar je die kennis gewoon nodig hebt, maar goed dat is een andere discussie (Bram, kom er maar in ...).quote:
Je hebt:
y = 3000∙1,05x = 3000∙(eln(1,05))x = 3000∙ex∙ln(1,05) = eln(3000)∙ex∙ln(1,05) = eln(3000)+x∙ln(1,05).
That's all.
)