SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Dat kan je in principe exact oplossen (wel lelijk).quote:Op zondag 20 mei 2012 23:47 schreef Amoeba het volgende:
Godverdomme, ik vermenigvuldig 2x met 3 bij c. Inderdaad, de vergelijking is x^3 - 3x + 1 = 0
En die heb ik nooit gehad. Zat wel even te kijken, maar ik heb nu staan:
m3 + n3 + 3mn(m+n) -3(m+n) + 1 = 0
Met x = m+n
en 3mn = 3 ofwel mn = 1
m3 + n3 + 3mn(m+n) -3(m+n) + 1 = 0
Met x = m+n
en 3mn = 3 ofwel mn = 1
Riparius, dan ga ik met de ABCD formule aan de gang.
Ik heb staan:
a3 -3a + 1 = 0
Grafisch geeft dit het juiste antwoord.
Nou goed, gaan we hier de ABCD formule op loslaten.
a = m+n
(m+n)3 -3(m+n) + 1 = 0
Dus
m3 + n3 + 3mn(m+n) -3(m+n) + 1 = 0
Dus 3mn = 3 ergo mn = 1
n = 1/m
Dus
m3 + 1/m3 + 1 = 0
Vermeningvuldigen met m3
m6 + m3 + 1 = 0
Substitutie naar q.
q = m3
q2 + q + 1 = 0
D = b2 -4ac
D = -3
Of moet ik hiermee verder rekenen..?
Ik heb staan:
a3 -3a + 1 = 0
Grafisch geeft dit het juiste antwoord.
Nou goed, gaan we hier de ABCD formule op loslaten.
a = m+n
(m+n)3 -3(m+n) + 1 = 0
Dus
m3 + n3 + 3mn(m+n) -3(m+n) + 1 = 0
Dus 3mn = 3 ergo mn = 1
n = 1/m
Dus
m3 + 1/m3 + 1 = 0
Vermeningvuldigen met m3
m6 + m3 + 1 = 0
Substitutie naar q.
q = m3
q2 + q + 1 = 0
D = b2 -4ac
D = -3
Of moet ik hiermee verder rekenen..?
Je bent zeker op de goede weg. Zoals inmiddels duidelijk is leidt het probleem tot een kubische vergelijking en die kun je in principe oplossen met de methode die aan Cardano wordt toegeschreven (maar niet van hem is), en dat is wat je hier ook doet. Maar nu loop je stuk op die negatieve discriminant ...quote:
Riparius, dan ga ik met de ABCD formule aan de gang.
Ik heb staan:
a3 -3a + 1 = 0
Grafisch geeft dit het juiste antwoord.
Nou goed, gaan we hier de ABCD formule op loslaten.
a = m+n
(m+n)3 -3(m+n) + 1 = 0
Dus
m3 + n3 + 3mn(m+n) -3(m+n) + 1 = 0
Dus 3mn = 3 ergo mn = 1
n = 1/m
Dus
m3 + 1/m3 + 1 = 0
Vermeningvuldigen met m3
m6 + m3 + 1 = 0
Substitutie naar q.
q = m3
q2 + q + 1 = 0
D = b2 -4ac
D = -3
Of moet ik hiermee verder rekenen..?
i*wortel 3. Ik ga verder.quote:
[..]
Je bent zeker op de goede weg. Zoals inmiddels duidelijk is leidt het probleem tot een kubische vergelijking en die kun je in principe oplossen met de methode die aan Cardano wordt toegeschreven (maar niet van hem is), en dat is wat je hier ook doet. Maar nu loop je stuk op die negatieve discriminant ...
Ik heb net CE Wiskunde B gehad, en het beginnetje van complexe getallen van Wiskunde D gehad. Het is geen ramp als me dit niet lukt.
ABCD formule wist ik enkel het bestaan van trouwens.
ABCD formule wist ik enkel het bestaan van trouwens.
Nougoed, dan heb ik q = -.5 ± .5 i rt 3
Als ik dan alles terugreken naar a kom ik uit op in beide gevallen uit op 1,53 (zegt mijn GR)
Ik zat nu wel op wolframalpha naar het definitieve antwoord te kijken, maar nee, geen idee hoe ze daaraan komen.
Ofwel:
Waar dit het antwoord was waar ik op uitkwam:
[ Bericht 25% gewijzigd door #ANONIEM op 21-05-2012 00:41:22 ]
Als ik dan alles terugreken naar a kom ik uit op in beide gevallen uit op 1,53 (zegt mijn GR)
Ik zat nu wel op wolframalpha naar het definitieve antwoord te kijken, maar nee, geen idee hoe ze daaraan komen.
Ofwel:
Waar dit het antwoord was waar ik op uitkwam:
[ Bericht 25% gewijzigd door #ANONIEM op 21-05-2012 00:41:22 ]
Ik snap trouwens niet waar het bij mij mis gaat. Ik probeerde bolcoördinaten toe te passen en dan bereken je dus
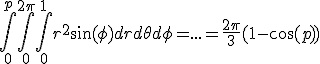
Dat moet gelijk zijn aan een kwart v/d inhoud van een bol, dus pi/3 .
Dus dan krijg je cos(p) = 1/2. Dus p=pi/3. Dat is dus de hoek t.o.v. het grondvlak. Dus sin(pi/3) = (hoogte van het snijvlak) / (straal (=1)) = hoogte van het snijvlak. Maar sin(pi/3)=0.8... veel te groot.
Dat moet gelijk zijn aan een kwart v/d inhoud van een bol, dus pi/3 .
Dus dan krijg je cos(p) = 1/2. Dus p=pi/3. Dat is dus de hoek t.o.v. het grondvlak. Dus sin(pi/3) = (hoogte van het snijvlak) / (straal (=1)) = hoogte van het snijvlak. Maar sin(pi/3)=0.8... veel te groot.
Tja, je GR zegt zoveel, maar de bedoeling was een exacte uitdrukking te geven, en het is toch duidelijk dat het antwoord reëel moet zijn en op het interval (0,1) moet liggen. Toch zit je best dichtbij.quote:
Nougoed, dan heb ik q = -.5 ± .5 i rt 3
Als ik dan alles terugreken naar a kom ik uit op in beide gevallen uit op 1,53 (zegt mijn GR)
Ik zat nu wel op wolframalpha naar het definitieve antwoord te kijken, maar nee, geen idee hoe ze daaraan komen.
Je hebt nu m3 = -½ + i∙½√3 en n3 = -½ - i∙½√3 (of omgekeerd),
aangezien het product van m3 en n3 gelijk moet zijn aan 1 omdat ook mn = 1, terwijl de som van m3 en n3 gelijk moet zijn aan -1 aangezien m3 + n3 + 1 = 0. Nu maar weer even zelf verder denken ...
Het lijkt erop alsof je hier het interval waarover je r neemt als constant beschouwt, maar dat is niet zo als je p varieert ...quote:
Ik snap trouwens niet waar het bij mij mis gaat. Ik probeerde bolcoördinaten toe te passen en dan bereken je dus
Ik snap je redenatie, maar uiteindelijk staan alle regels waar m en n aan moeten voldoen hier op papier. Blijkbaar wil je op een andere manier dan n = 1/m n en m 'ontrafelen'?
[ Bericht 0% gewijzigd door #ANONIEM op 21-05-2012 01:10:52 ]
[ Bericht 0% gewijzigd door #ANONIEM op 21-05-2012 01:10:52 ]
Je hebt de substitutie x = m + n gemaakt en onder de voorwaarde mn = 1 de waarden van m3 en n3 gevonden. Nu is het dus inderdaad zaak m en n te vinden, maar hoe ...quote:
Ik snap je redenatie, maar uiteindelijk staan alle regels waar m en n aan moeten voldoen hier op papier. Blijkbaar wil je op een andere manier van n = 1/m n en m 'ontrafelen'?
Als ik de vergelijkingen m6 + m3 +1 = 0 en m3 + n3 + 1 = 0 combineer kom ik uit dat m3*2 = n3 = m6
Uitgaande van de regel m3 = -½ + i∙½√3
(-½ + i∙½√3)3 = 1
Waarom heb ik totaal niet het gevoel dat mij dit verder helpt.
Uitgaande van de regel m3 = -½ + i∙½√3
(-½ + i∙½√3)3 = 1
Waarom heb ik totaal niet het gevoel dat mij dit verder helpt.
Dit is werkelijk echt wazig. Leuk probleempje zadel je me mee op, en ik kan bijna niet slapen voordat ik dit heb opgelost. Om half 5 eruit, en daarna een hele dag naar school...
Vooruit, verder.
Als m6 = n3 dan geldt natuurlijk ook m2 = n
Vooruit, verder.
Als m6 = n3 dan geldt natuurlijk ook m2 = n
Ik begrijp dat je het een fascinerend probleem vindt, en je zit ook op de goede weg, maar ik zou als ik jou was nu toch maar gaan slapen, anders is het zo half vijf en heb je geen bed gezien.quote:
Dit is werkelijk echt wazig. Leuk probleempje zadel je me mee op, en ik kan bijna niet slapen voordat ik dit heb opgelost. Om half 5 eruit, en daarna een hele dag naar school...
Ik kom er echt niet uit. m^6 = n^3 en m^2 = n
n√n= 1
n + √n = x
met n = 3√(-0.5 + 0.5i√3)
Waarom klopt dit niet
[ Bericht 1% gewijzigd door #ANONIEM op 21-05-2012 02:01:38 ]
n√n= 1
n + √n = x
met n = 3√(-0.5 + 0.5i√3)
Waarom klopt dit niet
[ Bericht 1% gewijzigd door #ANONIEM op 21-05-2012 02:01:38 ]
