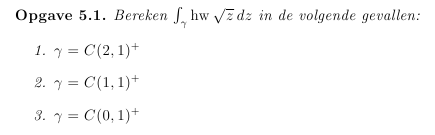SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Ik heb nog wat moeite met hoe complexe integralen werken.
De eerste is niet zo moeilijk. De functie is holomorf op een omgeving van de afsluiting van D = C(2,1), gesloten kromme, dus 0.
Bij de tweede gaat het al fout, omdat hw sqrt{z} niet gedefinieerd is in 't punt 0. Maar ik kan geloof ik niet de residuenstelling gebruiken, want dan moet het een geisoleerde singulariteit zijn, maar op die hele lijn (-\infty, 0] bestaat de functie niet.
De eerste is niet zo moeilijk. De functie is holomorf op een omgeving van de afsluiting van D = C(2,1), gesloten kromme, dus 0.
Bij de tweede gaat het al fout, omdat hw sqrt{z} niet gedefinieerd is in 't punt 0. Maar ik kan geloof ik niet de residuenstelling gebruiken, want dan moet het een geisoleerde singulariteit zijn, maar op die hele lijn (-\infty, 0] bestaat de functie niet.
Bij de tweede kun je over een deel van de cirkel integreren dat 0 niet bevat, en dan een limiet daarvan nemen zodat je pad in de limiet de hele cirkel is.quote:Op zaterdag 12 mei 2012 16:08 schreef Hanneke12345 het volgende:
Ik heb nog wat moeite met hoe complexe integralen werken.
[ afbeelding ]
De eerste is niet zo moeilijk. De functie is holomorf op een omgeving van de afsluiting van D = C(2,1), gesloten kromme, dus 0.
Bij de tweede gaat het al fout, omdat hw sqrt{z} niet gedefinieerd is in 't punt 0. Maar ik kan geloof ik niet de residuenstelling gebruiken, want dan moet het een geisoleerde singulariteit zijn, maar op die hele lijn (-\infty, 0] bestaat de functie niet.
Zoiets dus?
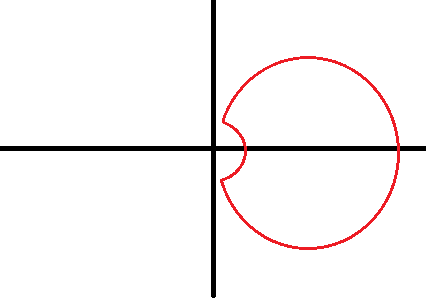
Kun je dan gewoon zeggen dat die limiet gelijk is aan de integraal? En de integraal over elk van die met dat halve bolletje eruit is 0 (zelfde argument als bij (a)) dus is het 0? Maar bij de derde werkt ook die truc niet meer, en is er nog altijd geen geisoleerde singulariteit
Kun je dan gewoon zeggen dat die limiet gelijk is aan de integraal? En de integraal over elk van die met dat halve bolletje eruit is 0 (zelfde argument als bij (a)) dus is het 0? Maar bij de derde werkt ook die truc niet meer, en is er nog altijd geen geisoleerde singulariteit
De hoofdwaarde van √z voor z = r∙eiφ met -π < φ ≤ π en r ≥ 0 is √r∙eiφ/2 en daarmee gedefinieerd voor elke z ∈C. Maar inderdaad is deze functie alleen holomorf op C\(-∞,0].quote:
Ik heb nog wat moeite met hoe complexe integralen werken.
[ afbeelding ]
De eerste is niet zo moeilijk. De functie is holomorf op een omgeving van de afsluiting van D = C(2,1), gesloten kromme, dus 0.
Bij de tweede gaat het al fout, omdat hw sqrt{z} niet gedefinieerd is in 't punt 0. Maar ik kan geloof ik niet de residuenstelling gebruiken, want dan moet het een geisoleerde singulariteit zijn, maar op die hele lijn (-\infty, 0] bestaat de functie niet.
Bij ons is het geloof ik -π < φ < π, maar dat weet ik niet zeker. Kan ik zo gauw ook niet terugvidnen.
Je moet dan wel de integraal over dat kleine cirkeltje dan afschatten en laten zien dat dat in de limiet naar 0 gaat.quote:
Zoiets dus?
[ afbeelding ]
Kun je dan gewoon zeggen dat die limiet gelijk is aan de integraal? En de integraal over elk van die met dat halve bolletje eruit is 0 (zelfde argument als bij (a)) dus is het 0? Maar bij de derde werkt ook die truc niet meer, en is er nog altijd geen geisoleerde singulariteit
Bij de derde kun je het gewoon direct parametriseren.
Inderdaad, bij het tweede geval kom je door een limietbeschouwing tot de conclusie dat de integraal langs γ ook hier nul moet zijn, want de integraal langs de gesloten curve in je plaatje blijft 0, hoe klein je het boogje rond de oorsprong ook maakt.quote:
Zoiets dus?
[ afbeelding ]
Kun je dan gewoon zeggen dat die limiet gelijk is aan de integraal? En de integraal over elk van die met dat halve bolletje eruit is 0 (zelfde argument als bij (a)) dus is het 0? Maar bij de derde werkt ook die truc niet meer, en is er nog altijd geen geisoleerde singulariteit
Voor de derde opgave heb je z(φ) = eiφ als parametervoorstelling van je curve.
Kun je met dat bolletje niet zeggen dat de functie holomorf is op een omgeving van de afsluiting van dat gebied, en dus (stelling) dat de integraal over de rand 0 is? Omdat het dan weer gewoon een gesloten kromme is enzo.
Die derde ga ik even proberen met parametrizeren.
Die derde ga ik even proberen met parametrizeren.
De integraal over zo'n gesloten kromme is inderdaad 0, maar je moet nog wel aantonen dat alles in de limiet ook goed gaat. In dit voorbeeld is dat vrijwel triviaal, maar 't is wel goed om je daar in het algemeen bewust van te zijn.quote:
Kun je met dat bolletje niet zeggen dat de functie holomorf is op een omgeving van de afsluiting van dat gebied, en dus (stelling) dat de integraal over de rand 0 is? Omdat het dan weer gewoon een gesloten kromme is enzo.
Die derde ga ik even proberen met parametrizeren.
RIemann som
Ik heb 6 VWO WisB al afgerond, en iemand in het examentopic kwam aanzetten dat we Riemann sommen moeten beheersen (ofwel invoeren op de GR)
Maar hoe moest dat ookalweer!?
Ik gebruik Mathprint instellingen op de GR, als ik dan die somrij pak, welke waarden moet ik dan invullen? Ik ben heel die rotzooi vergeten
Gaan we even uit van de vraag dat ik de oppervlakte van x=2 tot x=24 wil weten van de functie 3^x - 9x
En ja, ik zou hier ook gewoon een integraal voor kunnen pakken, maar het gaat me nu specifiek om de Riemannsom
[ Bericht 16% gewijzigd door #ANONIEM op 13-05-2012 11:45:31 ]
Ik heb 6 VWO WisB al afgerond, en iemand in het examentopic kwam aanzetten dat we Riemann sommen moeten beheersen (ofwel invoeren op de GR)
Maar hoe moest dat ookalweer!?
Ik gebruik Mathprint instellingen op de GR, als ik dan die somrij pak, welke waarden moet ik dan invullen? Ik ben heel die rotzooi vergeten
Gaan we even uit van de vraag dat ik de oppervlakte van x=2 tot x=24 wil weten van de functie 3^x - 9x
En ja, ik zou hier ook gewoon een integraal voor kunnen pakken, maar het gaat me nu specifiek om de Riemannsom
[ Bericht 16% gewijzigd door #ANONIEM op 13-05-2012 11:45:31 ]
Je moet die xk op je intervalletje invullen waarvoor f(x) het grootst is, en ook de xk waarvoor f(x) het kleinst is.
Op Thabits manier krijg je een bovensom en ondersom (dus een bovengrens en ondergrens voor de integraal). Je kan ook steeds op ieder interval [xk, xk+1] de waarden in het midden nemen en daar f evalueren. Dan krijg je iets wat direct wat dichter bij de integraal zal zitten dan de ondersom of bovensom, en het is ook wat makkelijker te berekenen omdat je niet het supremum of infimum op ieder intervalletje hoeft te bepalen (dan moet je steeds nagaan of de functie daalt of stijgt op dat interval, etc).
Voorbeeld: Je moet het interval [2,24] opdelen in kleine deelintervalletjes. Je kan als grootte van die deelintervalletjes bijvoorbeeld 1 nemen (hoe kleiner, hoe dichter je bij de werkelijke integraal komt). Als je f dan steeds op de middens van die deelintervalletjes evalueert, moet je dus het volgende berekenen:
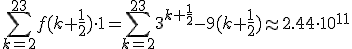
Terwijl
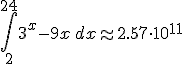
Dus dat zit nog redelijk in de buurt, ondanks het feit dat ik zulke grote deelintervallen heb genomen en je functie zo ontzettend hard stijgt
.
Voorbeeld: Je moet het interval [2,24] opdelen in kleine deelintervalletjes. Je kan als grootte van die deelintervalletjes bijvoorbeeld 1 nemen (hoe kleiner, hoe dichter je bij de werkelijke integraal komt). Als je f dan steeds op de middens van die deelintervalletjes evalueert, moet je dus het volgende berekenen:
Terwijl
Dus dat zit nog redelijk in de buurt, ondanks het feit dat ik zulke grote deelintervallen heb genomen en je functie zo ontzettend hard stijgt
.
Wat wil je oplossen? Wat is six?quote:Op zondag 13 mei 2012 13:24 schreef PizzaGeit het volgende:
Hoe los ik dit op?
Ik streepte deen de
tegen elkaar weg:
Klopt dit?
(six=6 ziet er wel logisch uit, net zoiets als two = 2?
)
quote:
Hoe los ik dit op?
Ik streepte de
Klopt dit?
Bijna, de 'echte' vraag is echter
The biggest argument against democracy is a five minute discussion with the average voter.
Thanks bro, je bent m'n held.quote:
Op Thabits manier krijg je een bovensom en ondersom (dus een bovengrens en ondergrens voor de integraal). Je kan ook steeds op ieder interval [xk, xk+1] de waarden in het midden nemen en daar f evalueren. Dan krijg je iets wat direct wat dichter bij de integraal zal zitten dan de ondersom of bovensom, en het is ook wat makkelijker te berekenen omdat je niet het supremum of infimum op ieder intervalletje hoeft te bepalen (dan moet je steeds nagaan of de functie daalt of stijgt op dat interval, etc).
Voorbeeld: Je moet het interval [2,24] opdelen in kleine deelintervalletjes. Je kan als grootte van die deelintervalletjes bijvoorbeeld 1 nemen (hoe kleiner, hoe dichter je bij de werkelijke integraal komt). Als je f dan steeds op de middens van die deelintervalletjes evalueert, moet je dus het volgende berekenen:
Terwijl
Dus dat zit nog redelijk in de buurt, ondanks het feit dat ik zulke grote deelintervallen heb genomen en je functie zo ontzettend hard stijgt
Maargoed, stel dat ik dan het als stapgrootte 1/10 wil nemen oid. Hoe moet dit dan? Ik probeerde het net, maar blijkbaar fout.
[ Bericht 3% gewijzigd door #ANONIEM op 13-05-2012 13:54:25 ]
hij zit grappig te doen, hij streept de n van sin(x) wegquote:
Lees je eigen post nog maar eens na, hier kan ik niks mee
Ik snap het nu pas... Beetje jammer dat hij 1/n erbij optelt in plaats van vermenigvuldigtquote:
[..]
hij zit grappig te doen, hij streept de n van sin(x) weg
aightquote:
Waar ik *1 doe moet het *0.1 worden. En je evalueert f dus op 2.05, 2.15, 2.25, ..., 23.95.quote:
(ninja dat je bent)
Zet het liever in gewone notatie ipv rekenmachinenotatie.
Je krijgt
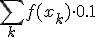
xk = 2+0.05k
Mag je zelf nadenken over welke k je precies moet sommeren.
Je krijgt
xk = 2+0.05k
Mag je zelf nadenken over welke k je precies moet sommeren.
Hoe doe je die gewone notatie? Via Wolframalpha ofzo?
Ik doe Wiskunde B, het enige waarvan ik die somformule ken is van die Riemannsom. Ik snap dan ook bar weinig van wat al die tekentjes betekenen. De bovenste was toch het aantal rechthoeken? En die onderste: geen idee
Ik doe Wiskunde B, het enige waarvan ik die somformule ken is van die Riemannsom. Ik snap dan ook bar weinig van wat al die tekentjes betekenen. De bovenste was toch het aantal rechthoeken? En die onderste: geen idee
We gingen zo snel over op integralen, dus ik ben heel die paragraaf in de loop van het jaar wel vergeten.
Het is gewoon een afkorting. Bijvoorbeeld:
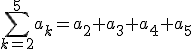
Dit heb je hopelijk toch ook wel eens gezien bij rekenkundige rijen en meetkundige rijen.
Om te zien wat er gebeurt kan je het beste even voor jezelf een plaatje tekenen, en dan de bijbehorende som bedenken.
Dit heb je hopelijk toch ook wel eens gezien bij rekenkundige rijen en meetkundige rijen.
Om te zien wat er gebeurt kan je het beste even voor jezelf een plaatje tekenen, en dan de bijbehorende som bedenken.
Ik heb wel WisD, maar ook rijen is al een jaar terug. Ik heb dit jaar WisB gedaan (in 2 jaar) en volgend jaar WisD (dus ook in 2 jaar, omdat ik dit jaar geen WisD gedaan heb)
En jawel, ook die rotzooi stond in m'n GR
Maargoed, dat k=2, is dat het onderste limiet?
Die 5, staat dat voor het aantal rechthoeken -1?
En jawel, ook die rotzooi stond in m'n GR
Maargoed, dat k=2, is dat het onderste limiet?
Die 5, staat dat voor het aantal rechthoeken -1?
