WGR Werk, Geldzaken, Recht en de Beurs
Hier kun je alles kwijt over sollicitaties, werksituaties, belastingen, (handelen op) de beurs, hypotheken, beleggingen en salarissen, arbeidscontracten of geschillen met je (huis)baas. Alles over werk, geldzaken en recht dus.
Hier op dit forum is al vaak geschreven over de rol van randomness in trading. Over patronen die we denken te herkennen in random processen en ook over hoe makkelijk we bepaalde trading resultaten toeschrijven aan "skills" (of het ontbreken daarvan). In dit topic wil ik één van de grootste mindf*cks bespreken van een random walk: de Arcsine Law.
Een makkelijk te begrijpen equivalent van trading zonder "edge" is het opwerpen van een muntje en dit blijven herhalen. Als de uitkomst "kop" is dan winnen we $1 en als het "munt" is dan verliezen we $1. De uitkomst hiervan is de bekende random walk. Om dit proces te bekijken gaan we eens 10 verschillende traders dit systeem laten handelen. Ze spelen tegen "de markt" dus niet tegen elkaar (ze kunnen theoretisch dus alle 10 tegelijkertijd winnen).
Als je 10 traders dit systeem laat handelen dan verwacht je gevoelsmatig misschien dat de totale winst van een individuele trader zal fluctueren rond de nullijn en dat na 1000 "trades" iedereen ongeveer op nul zal uitkomen. Immers, de kans op winst is even groot als de kans op verlies terwijl het te winnen of te verliezen bedrag beiden $1 is. Tevens verwacht je gevoelsmatig dat geen van de traders als een duidelijke winnaar uit de bus zal komen en dat de ranking van wie er aan kop staat en wie achteraan voortdurend zal wisselen gedurende het spel.
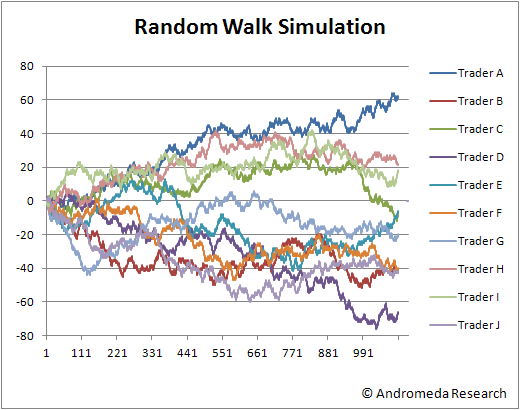
Echter, dit is geenzins het geval! Hieronder zie je de equitycurve van de 10 traders. Er zijn duidelijke winnaars en duidelijke verliezers. Ster traders en echte losers! En dat uit een volledig random proces! Hoe is dit mogelijk?
Welcome to the Arcsine Law. Je kunt wiskundig bewijzen dat de kansdichtheid dat een random walk trader een bepaalde tijd in de plus staat (of in de min) wordt gegeven door de volgende functie:
f(x) = 1 / ( π * sqrt( x * (1-x) ) ) met 0<x<1
Hierin is x de tijd dat een trader in de plus of in de min staat gedurende de beschouwde periode. Als we dit plotten krijgen we de volgende grafiek:
Dus stel dat we de trading performance bekijken van een trader over de periode van een jaar, dan geeft dit aan dat de kans dat een trader 6 maanden van de tijd positief staat en 6 maanden negatief veel kleiner is dan de kans dat hij 1 maand positief staat en 11 maanden negatief, of dat hij 1 maand negatief staat en 11 maanden positief.
Dit verklaart het resultaat van de simulatie. Als ik de trading periode verdeel in 100 dagen met elk 11 trades en ik kijk welk percentage van die 100 dagen er positief eindigden en welk percentage negatief dan krijg ik het volgende plaatje:
Dit plaatje is niet echt opmerkelijk. Er zijn duidelijk een paar traders die meer geluk hebben gehad dan anderen maar het fluctueert toch mooi rond de 50%, wat je ook zou verwachten.
Als ik echter een plaatje maak met het percentage van de tijd dat de trader in de plus stond of in de min over de hele periode van 100 dagen dan zie je duidelijk die Arcsine functie terug: ofwel ze staan bijna de hele periode op winst, ofwel ze staan bijna de hele periode op verlies.
Uit de Arcsine Law volgt tevens dat iemand die eenmaal op voorsprong staat een grote kans heeft om die te behouden, evenals iemand die op achterstand staat dat niet snel meer inhaalt. Trader A is een eindbaas kwa total return en Trader I is weliswaar minder winstgevend maar staat vanaf dag één op winst en heeft nooit negatief gestaan! Trader B, F en vooral J zijn een absolute mislukking. Zij zijn gelijk op de eerste dag in de verliezen gedoken en zijn daar nooit meer bovenop gekomen.
Het is bijna niet te geloven, maar dit is het resultaat van een volledig random proces! En geen cherry-picking hier, je kunt deze simulatie zelf gemakkelijk dupliceren in Excel.
Komen dit soort resultaten je bekend voor uit de praktijk? Mensen waarvan je weet dat ze niet liegen en toch al een heel jaar al in de plus staan (of juist in de min)? Je weet nu waarom!
Een makkelijk te begrijpen equivalent van trading zonder "edge" is het opwerpen van een muntje en dit blijven herhalen. Als de uitkomst "kop" is dan winnen we $1 en als het "munt" is dan verliezen we $1. De uitkomst hiervan is de bekende random walk. Om dit proces te bekijken gaan we eens 10 verschillende traders dit systeem laten handelen. Ze spelen tegen "de markt" dus niet tegen elkaar (ze kunnen theoretisch dus alle 10 tegelijkertijd winnen).
Als je 10 traders dit systeem laat handelen dan verwacht je gevoelsmatig misschien dat de totale winst van een individuele trader zal fluctueren rond de nullijn en dat na 1000 "trades" iedereen ongeveer op nul zal uitkomen. Immers, de kans op winst is even groot als de kans op verlies terwijl het te winnen of te verliezen bedrag beiden $1 is. Tevens verwacht je gevoelsmatig dat geen van de traders als een duidelijke winnaar uit de bus zal komen en dat de ranking van wie er aan kop staat en wie achteraan voortdurend zal wisselen gedurende het spel.
Echter, dit is geenzins het geval! Hieronder zie je de equitycurve van de 10 traders. Er zijn duidelijke winnaars en duidelijke verliezers. Ster traders en echte losers! En dat uit een volledig random proces! Hoe is dit mogelijk?
Welcome to the Arcsine Law. Je kunt wiskundig bewijzen dat de kansdichtheid dat een random walk trader een bepaalde tijd in de plus staat (of in de min) wordt gegeven door de volgende functie:
f(x) = 1 / ( π * sqrt( x * (1-x) ) ) met 0<x<1
Hierin is x de tijd dat een trader in de plus of in de min staat gedurende de beschouwde periode. Als we dit plotten krijgen we de volgende grafiek:
Dus stel dat we de trading performance bekijken van een trader over de periode van een jaar, dan geeft dit aan dat de kans dat een trader 6 maanden van de tijd positief staat en 6 maanden negatief veel kleiner is dan de kans dat hij 1 maand positief staat en 11 maanden negatief, of dat hij 1 maand negatief staat en 11 maanden positief.
Dit verklaart het resultaat van de simulatie. Als ik de trading periode verdeel in 100 dagen met elk 11 trades en ik kijk welk percentage van die 100 dagen er positief eindigden en welk percentage negatief dan krijg ik het volgende plaatje:
Dit plaatje is niet echt opmerkelijk. Er zijn duidelijk een paar traders die meer geluk hebben gehad dan anderen maar het fluctueert toch mooi rond de 50%, wat je ook zou verwachten.
Als ik echter een plaatje maak met het percentage van de tijd dat de trader in de plus stond of in de min over de hele periode van 100 dagen dan zie je duidelijk die Arcsine functie terug: ofwel ze staan bijna de hele periode op winst, ofwel ze staan bijna de hele periode op verlies.
Uit de Arcsine Law volgt tevens dat iemand die eenmaal op voorsprong staat een grote kans heeft om die te behouden, evenals iemand die op achterstand staat dat niet snel meer inhaalt. Trader A is een eindbaas kwa total return en Trader I is weliswaar minder winstgevend maar staat vanaf dag één op winst en heeft nooit negatief gestaan! Trader B, F en vooral J zijn een absolute mislukking. Zij zijn gelijk op de eerste dag in de verliezen gedoken en zijn daar nooit meer bovenop gekomen.
Het is bijna niet te geloven, maar dit is het resultaat van een volledig random proces! En geen cherry-picking hier, je kunt deze simulatie zelf gemakkelijk dupliceren in Excel.
Komen dit soort resultaten je bekend voor uit de praktijk? Mensen waarvan je weet dat ze niet liegen en toch al een heel jaar al in de plus staan (of juist in de min)? Je weet nu waarom!
"If you want to make God laugh, tell him about your plans"
Mijn reisverslagen
Mijn reisverslagen
Uit die statistiek volgt dan toch ook als we maar lang genoeg wachten dat iedereen op hetzelfde resultaat zou moeten uitkomen. Dat is alleen het probleem met statistiek en kansberekening als je te beleggen geld maar oneindig zou zijn, zou je gewoon op de casino (rood/ zwart / oneindige grote inzet) manier steeds je inzet moeten verdubbelen bij verlies. 
Leuk! Maar is het practische nut hiervan alleen om het succes of verlies van traders te relativeren (omdat zelfs bij een 50-50 strategie die geen enkel beleggingsinzicht vereist, er een grote diversiteit aan winnaars en verliezers ontstaat)?
Het zou leuk zijn als je in het profijt van een succesvolle trader kon delen, maar helaas: zodra je in zijn portefeuille stapt begint er voor jou een nieuwe tijdreeks waarin winst of verlies weer een geheel eigen richting kunnen kiezen - al blijft de oorspronkelijke trader zijn voorsprong behouden.
Het zou leuk zijn als je in het profijt van een succesvolle trader kon delen, maar helaas: zodra je in zijn portefeuille stapt begint er voor jou een nieuwe tijdreeks waarin winst of verlies weer een geheel eigen richting kunnen kiezen - al blijft de oorspronkelijke trader zijn voorsprong behouden.
Nee! Een een maal behaalde voorsprong of achterstand blijft relatief vaak behouden. Wel heeft bij aanvang iedereen gelijke kansen om op een bepaalde winst of een bepaald verlies uit te komen, en zal het resultaat van alle traders samen, naarmate de tijd strekt, steeds dichter bij de 0 uitkomen.quote:Op woensdag 18 april 2012 14:20 schreef Basp1 het volgende:
Uit die statistiek volgt dan toch ook als we maar lang genoeg wachten dat iedereen op hetzelfde resultaat zou moeten uitkomen.
Tja... je mag dit verhaal vast niet in het casino komen vertellen...
"No, I do not believe in patents. I believe that patents make other people dis-incentied in coming up with new thing" - Thomas Peterffy
Ik denk dat het casino de slogan: "ook jij kunt trader a zijn' er bij zou zetten.quote:
Tja... je mag dit verhaal vast niet in het casino komen vertellen...
Veel mensen zullen naar de grafiek kijken en (zichzelf als winnaar beoordelende) denken dat er dus over langere tijd winst gemaakt kan worden.
Kun je de random walk aan passen naar een $1,05 winst en en $1,0 verlies? De beurs is geen zero sum game namelijk.
Een paar mensen hier missen het punt van dit topic compleet geloof ik.....
"If you want to make God laugh, tell him about your plans"
Mijn reisverslagen
Mijn reisverslagen
De arcsinusverdeling vind ik enorm contra-intuitief. Je kunt niet zonder meer aannemen dat de returns van een proces voorspellende waarde hebben als het proces zelf als onvoorspelbaarheid een rol speelt. Ik vind het moeilijk om te accepteren maar het verklaart wel waarom winning- en losing streaks voorkomen. Al met al, hulde voor de OP! Van dit soort topics kan iedereen die ook maar iets doet met beleggen veel van leren.
One man's trash, another man's treasure.
Ik vond het wel een goede verklaring voor het 'beursaap' effectquote:Op woensdag 18 april 2012 15:33 schreef SeLang het volgende:
Een paar mensen hier missen het punt van dit topic compleet geloof ik.....
Je kan als topper dus veel intelligenter zijn dan een chimpansee en als nog een waardeloze belegger zijn
"No, I do not believe in patents. I believe that patents make other people dis-incentied in coming up with new thing" - Thomas Peterffy
Ik had nog nooit van de Arcsine Law gehoord, maar ik geloof dat het statistisch gezien gewoon redelijk obvious is dat je ook in het geval van een random walk model (zoals kop/munt of de aandelenmarkt) na heel veel herhalingen ver van de 0 kan staan. Alleen wordt die kans kleiner naarmate n toeneemt, wat min of meer betekent dat je op langere termijn toch echt niet van het gemiddelde 0 kan afwijken. Niettemin leuk topic hoor, het wordt ongetwijfeld wel eens onderschat!
Ik heb niet meer zo'n rekenmachine van de middelbare, maar kan iemand die wel zo'n ding heeft berekenen wat er komt uit '1-binomcdf(1000,0.5,559)'? Daarmee reken je de kans uit dat je na 1000x kop of munt inderdaad op >60 uitkomt, zoals het geval is bij trader A in de OP. Ben wel benieuwd hoe waarschijnlijk het dan is dat je minstens zoveel geluk hebt als trader A.
Wat misschien dan nog veel leuker is, nu we toch bezig zijn, is om de termijn uit te rekenen die nodig is om zowel winners als losers in een random walk model statistisch zo goed als uit te sluiten. Bijvoorbeeld met '1-binomcdf(x,0.5,x/2*1,01)<0,01' en die dan voor x op te lossen. Kan iemand die ook eens intikken? Dan zou je het aantal dagen moeten krijgen waarvoor geldt dat statistisch gezien nog maar 1% van alle mensen een winstje zal maken dat de 1% ontstijgt (oftewel hoe lang het duurt voordat nog maar 1 op de 100 mensen de markt verslaat met meer dan een procentje terwijl dat puur geluk is).
Ik heb niet meer zo'n rekenmachine van de middelbare, maar kan iemand die wel zo'n ding heeft berekenen wat er komt uit '1-binomcdf(1000,0.5,559)'? Daarmee reken je de kans uit dat je na 1000x kop of munt inderdaad op >60 uitkomt, zoals het geval is bij trader A in de OP. Ben wel benieuwd hoe waarschijnlijk het dan is dat je minstens zoveel geluk hebt als trader A.
Wat misschien dan nog veel leuker is, nu we toch bezig zijn, is om de termijn uit te rekenen die nodig is om zowel winners als losers in een random walk model statistisch zo goed als uit te sluiten. Bijvoorbeeld met '1-binomcdf(x,0.5,x/2*1,01)<0,01' en die dan voor x op te lossen. Kan iemand die ook eens intikken? Dan zou je het aantal dagen moeten krijgen waarvoor geldt dat statistisch gezien nog maar 1% van alle mensen een winstje zal maken dat de 1% ontstijgt (oftewel hoe lang het duurt voordat nog maar 1 op de 100 mensen de markt verslaat met meer dan een procentje terwijl dat puur geluk is).
Het gecursiveerde is alleen van te voren gezien waar. Maar als jij eenmaal op winst staat, is de kans beter dan 50% dat je dat een miljoen gokjes later nog steeds staat. Gemiddeld zullen al die nieuwe gokjes immers op 0 uitkomen, en omdat je al op winst stond, is de verwachting dus dat je dat ook blijft staan; je graviteert niet langzaam naar de 0.quote:
[..] dat je ook in het geval van een random walk model (zoals kop/munt of de aandelenmarkt) na heel veel herhalingen ver van de 0 kan staan. Alleen wordt die kans kleiner naarmate n toeneemt, wat min of meer betekent dat je op langere termijn toch echt niet van het gemiddelde 0 kan afwijken.
Dat spreekt voor zich. Als je begint op 50 navigeer je gemiddeld naar 50 en niet weer terug naar 0. De verwachtingswaarde hangt puur af van het tijdstip waarop je begint te meten (maar goed, je geeft zelf ook al aan dat je dat doorhebt).
Niet waar, die kans wordt juist groter met n. Om precies te zijn schaalt de dispersie bij een ééndimensionale random walk metquote:
Ik had nog nooit van de Arcsine Law gehoord, maar ik geloof dat het statistisch gezien gewoon redelijk obvious is dat je ook in het geval van een random walk model (zoals kop/munt of de aandelenmarkt) na heel veel herhalingen ver van de 0 kan staan. Alleen wordt die kans kleiner naarmate n toeneemt, wat min of meer betekent dat je op langere termijn toch echt niet van het gemiddelde 0 kan afwijken. Niettemin leuk topic hoor, het wordt ongetwijfeld wel eens onderschat!
[...]
http://en.wikipedia.org/w(...)ensional_random_walk
Op dinsdag 23 augustus 2011 23:18 schreef problematiQue het volgende:
Mensen die zomaar claimen dat A beter is dan B moet je gewoon negeren. Internetruis.
Mensen die zomaar claimen dat A beter is dan B moet je gewoon negeren. Internetruis.
Ik heb het daar over een experiment die a priori bekeken wordt he. Dus aan het begin beslissen of je bij wijze van tot n=1000 of tot n=100.000 doorgaat en daar voordat je begint een kans aan te koppelen.
Interessant en hangt inderdaad samen met het door Gebraden_Wombat aangehaalde dispersie bij een random walk. Waarbij veel mensen het onjuiste geloof hebben dat bij een grotere n de kans juist toenoemt dat alles bij de 0 terecht komt.
Mochten de traders overigens ook failliet kunnen gaan bij te grote verliezen, dan is er weer de zekerheid dat ze op termijn allemaal failliet zijn.
p.s.
Je had je traders wel wat beter mogen scouten. 80% in de min en een rampzalig collectief verlies, wat een prutsers.
Mochten de traders overigens ook failliet kunnen gaan bij te grote verliezen, dan is er weer de zekerheid dat ze op termijn allemaal failliet zijn.
p.s.
Je had je traders wel wat beter mogen scouten. 80% in de min en een rampzalig collectief verlies, wat een prutsers.
Abre los ojos
Dat zou je verwachten maar dat blijkt dus niet zo te zijn.quote:
Dat spreekt voor zich. Als je begint op 50 navigeer je gemiddeld naar 50 en niet weer terug naar 0. De verwachtingswaarde hangt puur af van het tijdstip waarop je begint te meten (maar goed, je geeft zelf ook al aan dat je dat doorhebt).
Kan je me uitleggen waarom niet dan? Want dat druist dan in tegen alles wat ik over statistiek geleerd heb.
Daar ben ik er eentje van denk ik. Dit is toch statistiek 101? Je zal ongeveer 50% winnen en verliezen. Bij N=0 zal de verwachte waarde 0 zijn. Als je eenmaal na de n=1op verlies of winst staat zal de verwachte waarde vanf dat moment -1 of +1 zijn. Logisch dus dat als je eenmaal op winst staat, de kans dat je op winst blijft staan het grootst is.quote:
Een paar mensen hier missen het punt van dit topic compleet geloof ik.....
Maar ik gok dat ik het punt mis
.
Zie de post van SeLang en dan met name het plaatje van de probability density. 1 random persoon (!) zal waarschijnlijk dik winnen of dik verliezen en als je eenmaal aan de winnende/verliezende hand bent dan zul je dat ook blijven. Gemiddeld klopt het wel wat je zegt maar tussen de traders zelfs zit een enorm verschil en het convergeert niet naar elkaar toe, zie het eerste plaatje, de random walk.quote:
Kan je me uitleggen waarom niet dan? Want dat druist dan in tegen alles wat ik over statistiek geleerd heb.
SeLang heeft hiervoor wat wiskundige statistiek en wiskunde gebruikt om dit te beredeneren. De vraag is nu of het klopt met de werkelijkheid. Dat zou ik zelf niet weten. Wellicht dat jij een idee hebt?
Wat Kaas zei was correct. En ja, een eenmaal behaalde positie zal gemiddeld behouden blijven, maar het is niet zo dat iemand die al wat gewonnen heeft, een grotere kans heeft om daar bovenop nog méér te zullen winnen.quote:
Zie de post van SeLang en dan met name het plaatje van de probability density. 1 random persoon (!) zal waarschijnlijk dik winnen of dik verliezen en als je eenmaal aan de winnende/verliezende hand bent dan zul je dat ook blijven.
Ik weet niet wat jullie zien maar ik zie hierboven niet dat de random walk convergeert hoor.quote:
[..]
Wat Kaas zei was correct. En ja, een eenmaal behaalde positie zal gemiddeld behouden blijven, maar het is niet zo dat iemand die al wat gewonnen heeft, een grotere kans heeft om daar bovenop nog méér te zullen winnen.
Ik heb het laatste vanochtend inderdaad niet goed geformuleerd. Het betekent dat van een random persoon over een jaar de kans groter is dat hij in dat jaar qua tijd dikker wint of verliest dan dat hij gelijk zou draaien. Enfin, zie de uitleg van SeLang. Ik schep alleen maar onduidelijkheid omdat ik het zelf niet geheel snap.
En Kaas ik kan het daarom moeilijk uitleggen. Maar jij beweert nu precies wat SeLang probeerde te ontkrachtte in zijn openingspost.
Dat beweert dan ook niemand! Integendeel juist.quote:
[..]
Ik weet niet wat jullie zien maar ik zie hierboven niet dat de random walk convergeert hoor.
Dat denk ik ook..quote:Ik schep alleen maar onduidelijkheid omdat ik het zelf niet geheel snap.
Nee dat betekent het niet. Het betekent dat wanneer je op winst staat, de kans groter is dat je dat na N keer nog steeds staat, dan dat je dan op verlies staat. Het betekent dus niet dat de kans op een dikke winst of dik verlies bij N=0 groter is dan dan quite draaien. De kans is in dit geval gewoon een normaal verdeling. (http://www.wolframalpha.com/input/?i=sequence+of+coin+flips+1000)quote:
Het betekent dat van een random persoon over een jaar de kans groter is dat hij in dat jaar qua tijd dikker wint of verliest dan dat hij gelijk zou draaien.
Er is geen beweging die ervoor zorgt dat je accelereert naar 'nog grotere winsten' (bij puur random).
Er is echter ook geen beweging die ervoor zorgt dat je weer naar de 0 toe schuift.
Je hebt gewoon vanaf elk meetpunt 50% kans om weer naar boven te gaan of naar beneden. Als je eerste 1000 trades je op +100 zetten, dan is de verwachting (bij random, 50/50) dat je na nog eens 1000 trades op 100 eindigd (met normale verdeling eromheen).
Er is echter ook geen beweging die ervoor zorgt dat je weer naar de 0 toe schuift.
Je hebt gewoon vanaf elk meetpunt 50% kans om weer naar boven te gaan of naar beneden. Als je eerste 1000 trades je op +100 zetten, dan is de verwachting (bij random, 50/50) dat je na nog eens 1000 trades op 100 eindigd (met normale verdeling eromheen).
I am a Chinese college students, I have a loving father, but I can not help him, he needs to do heart bypass surgery, I can not help him, because the cost of 100,000 or so needed, please help me, lifelong You pray Thank you!
Je traders representeren (bv) {4,3,2,1,0,-1,-2,-3,-4} sigma rond de verwachtingswaarde (0). En de standaarddeviatie groeit natuurlijk met de tijd, al was het maar omdat op t=1 een winst van meer dan 1 nog gewoon niet mogelijk is, en je op t=100 een (bijna) gaussian hebt die is opgespannen tussen -100 en 100.
Zoals? Returns zijn doorgaans niet binomiaal verdeeld lijkt me.quote:
De arcsinusverdeling vind ik enorm contra-intuitief. Je kunt niet zonder meer aannemen dat de returns van een proces voorspellende waarde hebben als het proces zelf als onvoorspelbaarheid een rol speelt. Ik vind het moeilijk om te accepteren maar het verklaart wel waarom winning- en losing streaks voorkomen. Al met al, hulde voor de OP! Van dit soort topics kan iedereen die ook maar iets doet met beleggen veel van leren.
More oneness, less categories
Open hearts, no strategies
Decisions based upon faith and not fear
People who live right now and right here
Open hearts, no strategies
Decisions based upon faith and not fear
People who live right now and right here
Zelf ook even gedaan:
eh dat moet zijn: 8 traders
eh dat moet zijn: 8 traders
Gemiddelde hier was 42 trouwens
Gemiddelde waarde van trade #50.000 bij 100 traders = 18 trouwens
eh dat moet zijn: 8 traders
eh dat moet zijn: 8 traders
Gemiddelde hier was 42 trouwens
Gemiddelde waarde van trade #50.000 bij 100 traders = 18 trouwens
I am a Chinese college students, I have a loving father, but I can not help him, he needs to do heart bypass surgery, I can not help him, because the cost of 100,000 or so needed, please help me, lifelong You pray Thank you!
Ah oke, ik zie dat we allemaal hetzelfde bedoelen en snappen, maar dat we het wellicht (waaronder ik zelf) niet duidelijk genoeg omschreven.
Toch een heel tof topic, want ondanks dat ik wist dat je een normale verdeling rondom de nullijn zou hebben had ik totaal niet verwacht dat de verschillen op termijn zo groot zouden worden. Zat ik toch iets te vast in mijn denken dat alles op termijn wel dichtbij de 0 zou zitten.
Toch een heel tof topic, want ondanks dat ik wist dat je een normale verdeling rondom de nullijn zou hebben had ik totaal niet verwacht dat de verschillen op termijn zo groot zouden worden. Zat ik toch iets te vast in mijn denken dat alles op termijn wel dichtbij de 0 zou zitten.
Als je even nadenkt over wat een random walk is (en plaatjes plotten verduidelijkt het enorm) dan is het allemaal evident, zoals sommige mensen hier al aangeven. Maar als je mensen op voorhand vraagt wat een grotere kans is:
1) Dat een trader's Profit&Loss voor het lopende jaar 6 maanden van het jaar positief is en 6 maanden van het jaar negatief
of
2) Dat een trader's Profit&Loss voor het lopende jaar 1 maand van het jaar positief is en 11 maanden negatief of 1 maand negatief en 11 maanden positief.
Dan kiest bijna iedereen voor 1) terwijl juist 2) een veel grotere kans is. Dat is dus de Arcsine Law. Misschien had ik het topic beter met die vraag kunnen beginnen zonder meteen het antwoord in de OP te zetten.
1) Dat een trader's Profit&Loss voor het lopende jaar 6 maanden van het jaar positief is en 6 maanden van het jaar negatief
of
2) Dat een trader's Profit&Loss voor het lopende jaar 1 maand van het jaar positief is en 11 maanden negatief of 1 maand negatief en 11 maanden positief.
Dan kiest bijna iedereen voor 1) terwijl juist 2) een veel grotere kans is. Dat is dus de Arcsine Law. Misschien had ik het topic beter met die vraag kunnen beginnen zonder meteen het antwoord in de OP te zetten.
"If you want to make God laugh, tell him about your plans"
Mijn reisverslagen
Mijn reisverslagen
Dat had wel geholpen, want mijn antwoord was dan in eerste instantie ook 1 geweest. Weer wat geleerd!
Bedoel je dat het 11 maanden lang elke maand een negatieve winst heeft of dat de som van die 11 maanden negatief is (met eventueel een paar maanden positief), of dat de som van 12 maanden negatief is?
[ Bericht 11% gewijzigd door Zith op 20-04-2012 12:35:04 ]
[ Bericht 11% gewijzigd door Zith op 20-04-2012 12:35:04 ]
I am a Chinese college students, I have a loving father, but I can not help him, he needs to do heart bypass surgery, I can not help him, because the cost of 100,000 or so needed, please help me, lifelong You pray Thank you!
De clue is dat een random walk de som is van binomiaal verdeelde variabelen, niet de gemiddelde som. Statistiek zegt dan weliswaar dat de verwachte waarde van die som normaal verdeeld is rond 0 (op termijn), maar ook dat de standaarddeviatie meegroeit met de lengte van die som (de hoeveelheid trades).quote:
Ah oke, ik zie dat we allemaal hetzelfde bedoelen en snappen, maar dat we het wellicht (waaronder ik zelf) niet duidelijk genoeg omschreven.
Toch een heel tof topic, want ondanks dat ik wist dat je een normale verdeling rondom de nullijn zou hebben had ik totaal niet verwacht dat de verschillen op termijn zo groot zouden worden.
...
More oneness, less categories
Open hearts, no strategies
Decisions based upon faith and not fear
People who live right now and right here
Open hearts, no strategies
Decisions based upon faith and not fear
People who live right now and right here
Nou ja, in het geval van een random walk zoals in de op zijn de returns een typische witte ruis dus als je daarop filtert houd je in principe niks over. Voor systemen waar wel duidelijk een statisch voordeel in zit houd je na ruisfiltering wel wat over aan het einde van de streep en die component kan best een verschoven binomiale verdeling als gevolg hebben. Als je de edge als component weet te isoleren dan kun je binnen een bepaald interval vaak voorspellen hoe het systeem zich gaat gedragen. Ik vind het dus opmerkelijk dat een random walk zich niet volgens dat patroon gedraagt. De richting van een random walk valt op basis van de returns dus niet te voorspellen voor beursgerelateerde zaken waar een tradetermijn van enkele jaren vaak gezien als bewijs wordt voor een succesvolle strategie.quote:Op vrijdag 20 april 2012 09:23 schreef trancethrust het volgende:
[..]
Zoals? Returns zijn doorgaans niet binomiaal verdeeld lijkt me.
One man's trash, another man's treasure.
Off topic, maar het schijnt nog niet zo gemakkelijk te zijn om voor de PC een échte 'random' functie te maken. Ik vraag me af in hoeverre dat aan zo'n (best forse) afwijking heeft bijgedragen.quote:
Gemiddelde waarde van trade #50.000 bij 100 traders = 18 trouwens
Dat wordt inderdaad gegenereerd met een pseudo-random reeks, maar het zal me verbazen als dat echt merkbare afwijkingen veroorzaakt op zo'n random walk simulatie.quote:
[..]
Off topic, maar het schijnt nog niet zo gemakkelijk te zijn om voor de PC een échte 'random' functie te maken. Ik vraag me af in hoeverre dat aan zo'n (best forse) afwijking heeft bijgedragen.
Ik wil nog altijd een keer een echte random generator maken door een timertje te starten en stoppen, getriggerd door radioactief verval. Moet simpel te maken zijn met een Geigerteller
"If you want to make God laugh, tell him about your plans"
Mijn reisverslagen
Mijn reisverslagen
Hangt van de random-functie van excel af. In het algemeen, met goede generators (mersenne twister bv.), zijn de resultaten gewoon prima. Verder is die gerapporteerde afwijking helemaal niet fors; zie mijn vorige post.quote:
[..]
Off topic, maar het schijnt nog niet zo gemakkelijk te zijn om voor de PC een échte 'random' functie te maken. Ik vraag me af in hoeverre dat aan zo'n (best forse) afwijking heeft bijgedragen.
More oneness, less categories
Open hearts, no strategies
Decisions based upon faith and not fear
People who live right now and right here
Open hearts, no strategies
Decisions based upon faith and not fear
People who live right now and right here
Wat zit er in dat bakje, zo'n stukje Braziliaans strand waar je in een uurtje 130x de Nederlandse jaardosis radioactieve straling opdoet?quote:
Ik wil nog altijd een keer een echte random generator maken door een timertje te starten en stoppen, getriggerd door radioactief verval. Moet simpel te maken zijn met een Geigerteller
Nog veel meer off-topic, maar kennen jullie de site van de gelouwerde astrofysicus Kees de Jager? Hij viert deze maand zijn 90e verjaardag en heeft een site waarop hij o.a. heel interessante dingen over de invloed van de zon op het klimaat schrijft. Zijn nieuwste webpresentatie gaat over neutrino's, waarvan de zon er 200 biljoen per seconde door je heenschiet. Eéns per week knalt er een precies in een atoomkern, waardoor je heel eventjes een kernreactor wordt. Leuk voor de liefhebbers van grote getallen en bizarre feitjes: http://www.cdejager.com/presentaties/
Ja, je schreef: "Statistiek zegt dan weliswaar dat de verwachte waarde van die som normaal verdeeld is rond 0 (op termijn), maar ook dat de standaarddeviatie meegroeit met de lengte van die som (de hoeveelheid trades)".quote:Op vrijdag 20 april 2012 17:37 schreef trancethrust het volgende:
Verder is die gerapporteerde afwijking helemaal niet fors; zie mijn vorige post.
Hoe je dat laatste bedoelt als verklaring voor de afwijking begrijp ik niet. Want die deviatie kan twee kanten op (winst of verlies) en daarom zou ik verwachten dat juist met het toenemen van het aantal trades de gemiddelde uitkomst steeds dichter bij de nul komt te liggen. Intuitief vind ik +18 na 50.000 trades een erg grote afwijking.
Oh wacht even.. Ik las het verkeerd! De afwijking van +18 was niet het gemiddelde over alle trades, maar alleen die van de 50.000e trade. Met 100 traders lijkt dat me idd. niet opvallend groot.
Nee een beetje grond uit de omgeving van een afgedankte Britse radium mijnquote:
[..]
Wat zit er in dat bakje, zo'n stukje Braziliaans strand waar je in een uurtje 130x de Nederlandse jaardosis radioactieve straling opdoet?
Goed, nu weer ontopic.....
"If you want to make God laugh, tell him about your plans"
Mijn reisverslagen
Mijn reisverslagen
Jep, het ging in dit geval meer over normalisatie; het gemiddelde nemen over alle getallen (i.t.t. alleen de som nemen als je kijkt naar 1 trader, of zoals bij dat laatste plaatje die som delen door alleen 100 ipv 100*50000).quote:
Oh wacht even.. Ik las het verkeerd! De afwijking van +18 was niet het gemiddelde over alle trades, maar alleen die van de 50.000e trade. Met 100 traders lijkt dat me idd. niet opvallend groot.
More oneness, less categories
Open hearts, no strategies
Decisions based upon faith and not fear
People who live right now and right here
Open hearts, no strategies
Decisions based upon faith and not fear
People who live right now and right here
|
|
