[Bèta wiskunde] Huiswerk- en vragentopic

maandag 30 april 2012 @ 19:41:37 #281

GlowMouse

l'état, c'est moi

De exponentiële functie is g(x) = b^x, de logaritmische functie is h(x) = log_bf(x). Je krijgt dan dat g(h(x)) = f(x).

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

maandag 30 april 2012 @ 19:54:12 #282

Riparius

quote:
Op maandag 30 april 2012 18:25 schreef Warren het volgende:
Ik ben even helemaal in de war wat betreft exponetiele functies. Stel je hebt: 2^log₂(x+1). Hier heb je een logaritmische functie die is ingeplugd in een exponentiele functie.

Is een beetje hetzelfde idee als bij vraag 7 van dat Vlaamse toelatingsexamen. Had je daar dan geen problemen mee?

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

maandag 30 april 2012 @ 19:55:22 #283

Warren

quote:
Op maandag 30 april 2012 19:41 schreef GlowMouse het volgende:
De exponentiële functie is g(x) = b^x, de logaritmische functie is h(x) = log_bf(x). Je krijgt dan dat g(h(x)) = f(x).

Bedankt, dus g(x) = 2^x en h(x) = log₂(x+1)? Dan wordt h(g(x)) = log₂(2^x+1). Dat laatste ziet er wel fout uit, maar ik zou toch gewoon waar x staat in de logaritmische formule, 2^x moeten kunnen invullen?

quote:
Op maandag 30 april 2012 19:54 schreef Riparius het volgende:

[..]

Is een beetje hetzelfde idee als bij vraag 7 van dat Vlaamse toelatingsexamen. Had je daar dan geen problemen mee?

Nog niet naar gekeken.

maandag 30 april 2012 @ 20:05:18 #284

Riparius

quote:
Op maandag 30 april 2012 19:55 schreef Warren het volgende:

[..]

Bedankt, dus g(x) = 2^x en h(x) = log₂(x+1)? Dan wordt h(g(x)) = log₂(2^x+1). Dat laatste ziet er wel fout uit, maar ik zou toch gewoon waar x staat in de logaritmische formule, 2^x moeten kunnen invullen?

Je kunt natuurlijk allerlei functies samenstellen, daar is niets fout aan. Maar het helpt je niet zoveel met de oorspronkelijke opgave die je hierboven post. Houd vooral de definitie van de logaritme in gedachten: ^glog a is de exponent waartoe je het grondtal g moet verheffen om a te krijgen.

Als ik de logaritme van a met grondtal 2 nu even aangeef met lb a (officiële ISO aanbeveling) dan is dus lb(x + 1) de exponent waartoe ik 2 moet verheffen om x + 1 te krijgen, zodat per definitie geldt 2^lb(x+1) = x + 1. Dat is eigenlijk alles.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

maandag 30 april 2012 @ 22:41:36 #285

Bram_van_Loon

Jeff, we can!

Toen ik leerde met logaritmes te werken vond ik het handig om steeds met het grondtal 10 de formules af te leiden.
In dit geval (ik laat het grondtal even weg) zou ik dan dus invullen 10^log(1000) = 10^3 = 1000 en dan zie je direct weer hoe het zit.
Uiteindelijk moet je ernaar streven dat je dit soort truucjes niet nodig hebt maar op het moment dat je inzicht nog wat minder is dan kan het naar mijn ervaring veel helpen.

ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL

woensdag 2 mei 2012 @ 16:43:49 #286

Dale.

Vraagje er zijn hier vast ook mensen bekend met Matlab... Maar hoe implementeer je de finit-difference method in Matlab? 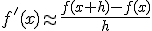$f'(x) \approx \frac{f(x + h) - f(x)}{h}$ . (dit moet met een functie)

Mijn probleem is is dat ik niet echt weet hoe ik een functie (x^2, exp(2*x^3 + 4), etc...) doorgeef aan een matlab functie... Ik heb nu, waarbij x een scalar is en h een vector en func zou dus de functie moeten zijn... sin(x), cos(x) kan ik nu wel meegeven maar bijvoorbeeld x^2 niet... Hoe doe ik dit?

1
2
3

function y = df(func,x,h)
y = (func(x + h) - func(x))./h;
end

woensdag 2 mei 2012 @ 16:52:14 #287

GlowMouse

l'état, c'est moi

http://www.mathworks.nl/help/techdoc/matlab_prog/f4-70115.html

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

woensdag 2 mei 2012 @ 17:34:13 #288

Dale.

quote:
Op woensdag 2 mei 2012 16:52 schreef GlowMouse het volgende:
http://www.mathworks.nl/help/techdoc/matlab_prog/f4-70115.html

Thanks!

donderdag 3 mei 2012 @ 10:15:11 #289

Dale.

Ik moet bewijzen dat de limiet van $\lim_{x\rightarrow\infty}2\sqrt{x}f(x) = 1$ is

alleen snap ik niet precies hoe dit kan want... $\lim_{x\rightarrow a} g(x)*f(x) = \lim_{x\rightarrow a} g(x) * \lim_{x\rightarrow a} f(x)$

$\lim_{x\rightarrow\infty}2\sqrt{x} * \lim_{x\rightarrow\infty}f(x) = \infty \cdot \lim_{x\rightarrow\infty}f(x)= \infty$

donderdag 3 mei 2012 @ 10:17:19 #290

Haushofer

Als je

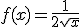
$f(x) = \frac{1}{2\sqrt{x}}$

kiest ben je klaar.

Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071

donderdag 3 mei 2012 @ 10:18:01 #291

Haushofer

Oftewel: volgens mij moet je f(x) nog geven

Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071

donderdag 3 mei 2012 @ 10:20:22 #292

Dale.

quote:
Op donderdag 3 mei 2012 10:18 schreef Haushofer het volgende:
Oftewel: volgens mij moet je f(x) nog geven

Ja zit net nog de hele opgave door te lezen blijkt dat ik over de definitie van f(x) heb gelezen

ik maar proberen een algeme definitie te vinden xD

donderdag 3 mei 2012 @ 11:16:21 #293

Dale.

Hmmmm vraagje dan.... 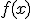$f(x)$ is dus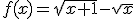 $f(x) = \sqrt{x+1} - \sqrt{x}$

dus dan

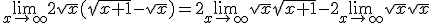
$\lim_{x\rightarrow\infty}2\sqrt{x}(\sqrt{x+1} - \sqrt{x}) = 2\lim_{x\rightarrow\infty}\sqrt{x}\sqrt{x+1} - 2\lim_{x\rightarrow\infty}\sqrt{x}\sqrt{x}$

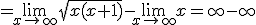
$= \lim_{x\rightarrow\infty}\sqrt{x(x+1)} - \lim_{x\rightarrow\infty}x = \infty - \infty$

terwijl het dus 1 moet zijn... waar maak ik de fout?

[ Bericht 0% gewijzigd door Dale. op 03-05-2012 11:21:40 ]

donderdag 3 mei 2012 @ 12:03:16 #294

Haushofer

Ik ben niet meer zo bekend met de rekenregeltjes voor limieten, dus of en wanneer je een product/som van limieten mag opsplitsen als de delen afzonderlijk geen limiet kennen weet ik niet; dat staat vast in je boek. Een uitdrukking als

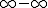
$\infty - \infty$

is sowieso niet gedefinieerd, dus daar moet al een belletje gaan rinkelen; waarschijnlijk mag je in dit geval dus die opsplitsing niet doen.

Maar ik denk dat voor dit geval het handig is om

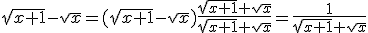
$\sqrt{x+1} - \sqrt{x} = (\sqrt{x+1} - \sqrt{x} ) \frac{\sqrt{x+1} + \sqrt{x}}{\sqrt{x+1} + \sqrt{x}} = \frac{1}{\sqrt{x+1} + \sqrt{x}}$

te schrijven en in je limiet te stoppen

Je krijgt dan

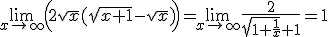
$\lim_{x \rightarrow \infty}\Bigl(2\sqrt{x}(\sqrt{x+1} - \sqrt{x}) \Bigr) = \lim_{x \rightarrow \infty } \frac{2}{\sqrt{1+ \frac{1}{x}} +1 } = 1$

Deze manier van omschrijven is vaak handig wanneer je met wortels hebt te maken.

[ Bericht 5% gewijzigd door Haushofer op 03-05-2012 12:11:03 ]

Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071

donderdag 3 mei 2012 @ 13:29:15 #295

Bram_van_Loon

Jeff, we can!

Dale, in jouw reactie van 10u15 klopt die laatste redenering volgens mij niet.
Neem voor f(x) bijvoorbeeld 1/x^3.

quote:
Deze manier van omschrijven is vaak handig wanneer je met wortels hebt te maken.

Dat lijkt mij een prima advies.

ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL

donderdag 3 mei 2012 @ 13:40:52 #296

Dale.

quote:
Op donderdag 3 mei 2012 13:29 schreef Bram_van_Loon het volgende:
Dale, in jouw reactie van 10u15 klopt die laatste redenering volgens mij niet.
Neem voor f(x) bijvoorbeeld 1/x^3.

Klopt, wist ik ook stiekem in mijn achterhoofd ;-), was er toen vanuit gegaan dat de eventuele teller >= noemer. Maar goed f(x) was blijkbaar gewoon gedefinieerd.

donderdag 3 mei 2012 @ 18:45:09 #297

Riparius

quote:
Op donderdag 3 mei 2012 11:16 schreef Dale. het volgende:
Hmmmm vraagje dan.... $f(x)$ is dus $f(x) = \sqrt{x+1} - \sqrt{x}$

dus dan

$\lim_{x\rightarrow\infty}2\sqrt{x}(\sqrt{x+1} - \sqrt{x}) = 2\lim_{x\rightarrow\infty}\sqrt{x}\sqrt{x+1} - 2\lim_{x\rightarrow\infty}\sqrt{x}\sqrt{x}$

$= \lim_{x\rightarrow\infty}\sqrt{x(x+1)} - \lim_{x\rightarrow\infty}x = \infty - \infty$

terwijl het dus 1 moet zijn... waar maak ik de fout?

Je fundamentele denkfout is dat je denkt dat je het symbool ∞ mag behandelen als een gewoon getal, maar dat is niet zo, ∞ is geen getal. Je mag dus ook niet zeggen dat een bepaalde limiet of een bepaalde grootheid 'gelijk' is aan 'oneindig', dat heeft geen betekenis. De rekenregel dat de limiet van een verschil van twee uitdrukkingen gelijk is aan het verschil van de limieten van die beide uitdrukkingen geldt ook alleen maar als de limieten van beide termen elk afzonderlijk bestaan, en dat is hier niet het geval.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

donderdag 3 mei 2012 @ 19:02:20 #298

thenxero

quote:
Op donderdag 3 mei 2012 18:45 schreef Riparius het volgende:

[..]

Je mag dus ook niet zeggen dat een bepaalde limiet of een bepaalde grootheid 'gelijk' is aan 'oneindig', dat heeft geen betekenis.

Je kan er wel een betekenis aan geven.

$\lim_{k\to\infty} k = \infty$

betekent dat in de limiet k groter is dan ieder reëel getal.

Met wat basis rekenregels kan je dan ook met oneindig rekenen (oneindig + oneindig = oneindig, oneindig *oneindig = oneindig, etc). Alleen oneindig - oneindig en oneindig/oneindig kan je niet definiëren.

donderdag 3 mei 2012 @ 19:34:09 #299

Riparius

quote:
Op donderdag 3 mei 2012 19:02 schreef thenxero het volgende:

[..]

Je kan er wel een betekenis aan geven.

$\lim_{k\to\infty} k = \infty$

betekent dat in de limiet k groter is dan ieder reëel getal.

Ik begrijp wat ermee wordt bedoeld, maar deze notatie is niettemin fout of op zijn minst onwenselijk, omdat deze aanleiding geeft tot precies het soort misverstanden als waar Dale blijk van geeft. In het verleden (tot in het begin van de 20e eeuw) noteerde men bijv. ook lim_x=∞ waar we nu lim_x→∞ schrijven, en dat gebeurt op goede gronden, namelijk om de indruk te vermijden dat je ∞ zou mogen behandelen als een getal.

quote:
Met wat basis rekenregels kan je dan ook met oneindig rekenen (oneindig + oneindig = oneindig, oneindig *oneindig = oneindig, etc). Alleen oneindig - oneindig en oneindig/oneindig kan je niet definiëren.

Didactisch is dat helemaal fout, want als je zegt dat je ∞ bij zichzelf kunt optellen of met zichzelf kunt vermenigvuldigen, dan kun je er gewoon op wachten totdat iemand als Dale aan komt zetten met het idee dat ∞ - ∞ gelijk is aan 0 of dat ∞/∞ gelijk is aan 1.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

donderdag 3 mei 2012 @ 19:43:50 #300

thenxero

quote:
Didactisch is dat helemaal fout, want als je zegt dat je ∞ bij zichzelf kunt optellen of met zichzelf kunt vermenigvuldigen, dan kun je er gewoon op wachten totdat iemand als Dale aan komt zetten met het idee dat ∞ - ∞ gelijk is aan 0 of dat ∞/∞ gelijk is aan 1.

In wat geavanceerdere boeken kom je het wel eens tegen.

donderdag 3 mei 2012 @ 20:06:04 #301

GlowMouse

l'état, c'est moi

Convexe analyse zonder ∞ als toevoeging aan de reële getallen (waardoor je sommige eigenschappen van een lichaam verliest) is niet te doen.

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

Forum Opties
Forumhop:
Hop naar:	(afkorting, bv 'KLB')

» school, studie en onderwijs

» school, studie en onderwijs