SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Ik bedoelde naar x, we doen hetzelfde 
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Zie alleen niet in hoe jij er vanaf hier bij komt dat deze 2e afgeleide positief (> of >= 0?) is wanneer
a(yb - (2-a) * (xa + yb)) .= 0 is. Die tweede regel (wanneer de determinant van de hessian positief is) kan ik ook niet achterhalen hoe je daarbij komt


Vanaf daar zou het mij ook niet lukken, dat is niet te lezen. Maar ik zie al dingen staan met ^{3/2} en een wortel, daarvan weet je dat het niet negatief is.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Sorry voor de onduidelijke post..
Maar kom er nog niet uit hoe jij vanuit:
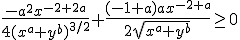
tot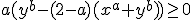 komt?
komt?
En hoe kun je deze dan verder oplosssen voor alle waarden van a&b?
Dat snap ik dus voor de determinant van de gehele hessiaan ook niet, alleen waarschijnlijk snap ik die wel als ik deze eerste snap! bedankt alvast!
Maar kom er nog niet uit hoe jij vanuit:
tot
En hoe kun je deze dan verder oplosssen voor alle waarden van a&b?
Dat snap ik dus voor de determinant van de gehele hessiaan ook niet, alleen waarschijnlijk snap ik die wel als ik deze eerste snap! bedankt alvast!


Voor strict concaaf moeten de determinant en de eigenwaardes van de Hessiaan positief zijn. Waarom dan het gelijk-aan-of-groter teken? Of is dit nog niet de (juiste) oplossing voor het strict geval?


Die breuk kun je optellen door de noemers gelijk te maken. a-2 ziet er bovendien makkelijker uit dan -2+a. Daarna kun je zien dat de noemer positief is, en concludeer je dat de teller positief moet zijn. In de teller herken je nog een factor
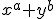
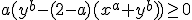
kun je schrijven als:
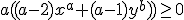
Wat b is maakt hier niet zo gek veel uit. Je kunt onderscheid maken tussen b=0 en b>0.
- Voor strict convex moet de dubbele afgeleide naar x strict positief zijn en de determinant ook.
- Voor gewoon convex moet ook de dubbele afgeleide naar y niet-negatief zijn.
Maar het probleem zat hem niet in de criteria
[ Bericht 0% gewijzigd door GlowMouse op 29-01-2012 22:59:53 ]
kun je schrijven als:
Wat b is maakt hier niet zo gek veel uit. Je kunt onderscheid maken tussen b=0 en b>0.
Ik ben inderdaad niet helemaal netjes met de tekens. Eigenlijk moet je de volgende twee aanpassingen doen tov wat ik deed:quote:Op zondag 29 januari 2012 22:47 schreef zoem het volgende:
Voor strict concaaf moeten de determinant en de eigenwaardes van de Hessiaan positief zijn. Waarom dan het gelijk-aan-of-groter teken? Of is dit nog niet de (juiste) oplossing voor het strict geval?
- Voor strict convex moet de dubbele afgeleide naar x strict positief zijn en de determinant ook.
- Voor gewoon convex moet ook de dubbele afgeleide naar y niet-negatief zijn.
Maar het probleem zat hem niet in de criteria
[ Bericht 0% gewijzigd door GlowMouse op 29-01-2012 22:59:53 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Nouja, als het groter of gelijk aan 0 is dan kan het nog wel convex zijn maar dan is het niet meer positief definiet. Maar dat heeft niets met deze opdracht te maken natuurlijk 
Ik denk dat als je de analytische vergelijkingen hebt, je vast wel elementen kan wegstrepen omdat deze toch positief zijn (zoals je zelf net al zei GM). Dingen als worteltrekken en even machten.
Ik denk dat als je de analytische vergelijkingen hebt, je vast wel elementen kan wegstrepen omdat deze toch positief zijn (zoals je zelf net al zei GM). Dingen als worteltrekken en even machten.


En allerlaatste vraag, hoe kom jij vanaf die (in mijn ogen) zeer complexe determinant van de Hessiaan tot ab(2+ab-a-2b) > 0 ? Bedankt voor de hulp


1/16 xa-2yb-2 wegdelen, ab buiten haakjes halen, xa+yb wegdelen, nog een keer door 2 delen, nog een xa+yb wegdelen 
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


12) Een onderzoeker voert een meta-analyse uit naar de correlatie tussen intelligentie van
Nederlandse ouders en dat van hun kinderen. Na combinatie van gegevens van 20
onderzoeken blijkt de correlatie tussen ouders en kinderen 0.75 te zijn, met een 95%
betrouwbaarheidsinterval dat loopt van [ 0.73 ; 0.77 ]. Welke conclusie kan op grond van
deze bevinding worden getrokken?
a) Er is waarschijnlijk geen verband tussen intelligentie van Nederlandse ouders en
hun kinderen
b) Er is waarschijnlijk een verband tussen de intelligentie van Nederlandse ouders en
hun kinderen, maar over de sterkte van dit verband valt niets te zeggen
c) Er is waarschijnlijk een verband tussen de intelligentie van Nederlandse ouders en
hun kinderen, en dit verband is tamelijk sterk
d) Er kan geen conclusie getrokken worden, omdat onbekend is hoe groot de
steekproeven van de 20 onderzoeken waren
Wie kan mij uitleggen wat het antwoord op deze vraag is en waarom?
Nederlandse ouders en dat van hun kinderen. Na combinatie van gegevens van 20
onderzoeken blijkt de correlatie tussen ouders en kinderen 0.75 te zijn, met een 95%
betrouwbaarheidsinterval dat loopt van [ 0.73 ; 0.77 ]. Welke conclusie kan op grond van
deze bevinding worden getrokken?
a) Er is waarschijnlijk geen verband tussen intelligentie van Nederlandse ouders en
hun kinderen
b) Er is waarschijnlijk een verband tussen de intelligentie van Nederlandse ouders en
hun kinderen, maar over de sterkte van dit verband valt niets te zeggen
c) Er is waarschijnlijk een verband tussen de intelligentie van Nederlandse ouders en
hun kinderen, en dit verband is tamelijk sterk
d) Er kan geen conclusie getrokken worden, omdat onbekend is hoe groot de
steekproeven van de 20 onderzoeken waren
Wie kan mij uitleggen wat het antwoord op deze vraag is en waarom?


Ik ben geen statistiek expert maar ik ga voor (c). De correlatie zit altijd tussen -1 en 1. Als het significant van 0 verschilt dan kan je spreken van correlatie. In (c) staat nog een woordje waarschijnlijk, omdat een statistische test altijd heel ver van de werkelijke waarde kan zitten (bijvoorbeeld doordat je niet willekeurig genoeg mensen hebt gekozen). Dus zeker ben je nooit.
(a) is pure onzin, (b) is onzin omdat de correlatie een maat is voor de sterkte. Bij (d) is er op zich wel het punt dat je steekproef groot genoeg moet zijn, maar omdat het confidence interval al [ 0.73 ; 0.77 ] is, is je steekproef kennelijk groot genoeg om te concluderen dat de correlatie significant groter dan 0 is.
(a) is pure onzin, (b) is onzin omdat de correlatie een maat is voor de sterkte. Bij (d) is er op zich wel het punt dat je steekproef groot genoeg moet zijn, maar omdat het confidence interval al [ 0.73 ; 0.77 ] is, is je steekproef kennelijk groot genoeg om te concluderen dat de correlatie significant groter dan 0 is.


a en d wegstrepen is simpel:
a. Zonder verband is de correlatie 0. Op grond van het betrouwbaarheidsinterval kun je de nulhypothese dat de correlatie 0 is, verwerpen.
d. de grootte van de steekproef zit verwerkt in de breedte van het betrouwbaarheidsinterval
Dan resteert de vraag hoe groot het verband is. Ik vind 'tamelijk sterk' een vaag begrip, maar dat er niets over valt te zeggen is ook niet waar (hoe groter de correlatie, hoe sterk het verband). Ik zou zeggen dat geen enkel antwoord echt goed is, maar c is de minst foute.
a. Zonder verband is de correlatie 0. Op grond van het betrouwbaarheidsinterval kun je de nulhypothese dat de correlatie 0 is, verwerpen.
d. de grootte van de steekproef zit verwerkt in de breedte van het betrouwbaarheidsinterval
Dan resteert de vraag hoe groot het verband is. Ik vind 'tamelijk sterk' een vaag begrip, maar dat er niets over valt te zeggen is ook niet waar (hoe groter de correlatie, hoe sterk het verband). Ik zou zeggen dat geen enkel antwoord echt goed is, maar c is de minst foute.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hoe duid je de index van het minimum van een rij getallen aan in wiskundige notatie? Meer specifiek, ik heb een matrix R en voor gegeven kolom k, zoek ik het minimum van die vector en daar weer de index j van.
Er staat me iets bij dat je min met de gewenste index letter er onder schrijft maar ik kan het niet terugvinden.
Ik heb nu dit
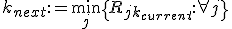
[ Bericht 14% gewijzigd door synthesix op 30-01-2012 12:42:08 ]
Er staat me iets bij dat je min met de gewenste index letter er onder schrijft maar ik kan het niet terugvinden.
Ik heb nu dit
[ Bericht 14% gewijzigd door synthesix op 30-01-2012 12:42:08 ]


Afhankelijk van je definitie van argmin moet je nog wat doen met een niet-uniek minimum.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Iemand enig idee hoe deze opgelost kan worden?
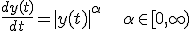
[ Bericht 2% gewijzigd door 123hopsaflops op 03-02-2012 12:27:04 ]
[ Bericht 2% gewijzigd door 123hopsaflops op 03-02-2012 12:27:04 ]


n/m
[ Bericht 73% gewijzigd door GlowMouse op 03-02-2012 12:39:14 ]
[ Bericht 73% gewijzigd door GlowMouse op 03-02-2012 12:39:14 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


verbeterdquote:Op vrijdag 3 februari 2012 12:22 schreef GlowMouse het volgende:
Is y afhankelijk van t?
Rare notatie van een interval.
Als je onderscheid maakt tussen y>=0 en y<0 dan is het toch wel te doen? Alleen opletten bij y=0 wanneer 0<alpha<=1.


Wat gebeurt er met je meetfout als je de meting een aantal keer herhaalt en dan het gemiddelde neemt? Bijvoorbeeld als ik een meetfout van 0,5 cm bij één meting heb en de meting 10x doe en dan het gemiddelde neem.
