SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Dit klopt niet want N(3) | N(1)=3 heeft een andere verdeling dan N(3).quote:Op maandag 16 januari 2012 22:34 schreef thenxero het volgende:
= E(N(3) - N(1) | N(1)=3) (vanwege "stationarity")
= E(N(3) - 3)


Ah, dus
E(N(4) - N(2) | N(1)=3)
= E(N(3) - N(1) | N(1)=3)
= E(N(3) | N(1) = 3) - 3
= E(N(2)) + 3 - 3
= 2k
En dan klopt het weer. Thanks.
E(N(4) - N(2) | N(1)=3)
= E(N(3) - N(1) | N(1)=3)
= E(N(3) | N(1) = 3) - 3
= E(N(2)) + 3 - 3
= 2k
En dan klopt het weer. Thanks.


Is er iemand die me op weg kan hen helpen met deze vraag over continuiteit?
[ Bericht 22% gewijzigd door Anoonumos op 18-01-2012 18:01:07 ]
[ Bericht 22% gewijzigd door Anoonumos op 18-01-2012 18:01:07 ]


Let niet op wat na = teken staat, ik heb het even in wolfram ingetypt zodat ik niet met LaTeX hoefde te kloten 
Evalueer over gebied D met D={(x,y)| |x|+|y|=<1}
(1) Ondergrens x en y zijn als |x| of |y| minimaal zijn voor |x|+|y|<=1, dat is voor x,y=-1 als y,x=0
(2) Bovengrens x en y zijn als |x| of |y| maximaal zijn voor |x|+|y|<=1, dat is voor x,y=1 als y,x=0
(3) Dus integreren naar x en y met beide grenzen van -1 naar 1
Klopt mijn gedachtegang??
Evalueer over gebied D met D={(x,y)| |x|+|y|=<1}
(1) Ondergrens x en y zijn als |x| of |y| minimaal zijn voor |x|+|y|<=1, dat is voor x,y=-1 als y,x=0
(2) Bovengrens x en y zijn als |x| of |y| maximaal zijn voor |x|+|y|<=1, dat is voor x,y=1 als y,x=0
(3) Dus integreren naar x en y met beide grenzen van -1 naar 1
Klopt mijn gedachtegang??


Gewoon even een plaatje tekenen hoe gebied D eruit ziet. Je krijgt dan een gebied dat wordt afgebakend door de vier lijnen |y|=1-|x|. Ja dat zijn vier lijnen, want |y|=+-y, |x|=+-x.quote:Op woensdag 18 januari 2012 18:54 schreef Physics het volgende:
Let niet op wat na = teken staat, ik heb het even in wolfram ingetypt zodat ik niet met LaTeX hoefde te kloten
Evalueer [ afbeelding ] over gebied D met D={(x,y)| |x|+|y|=<1}
(1) Ondergrens x en y zijn als |x| of |y| minimaal zijn voor |x|+|y|<=1, dat is voor x,y=-1 als y,x=0
(2) Bovengrens x en y zijn als |x| of |y| maximaal zijn voor |x|+|y|<=1, dat is voor x,y=1 als y,x=0
(3) Dus integreren naar x en y met beide grenzen van -1 naar 1
Klopt mijn gedachtegang??


Voor de x die de inversen zijn van een natuurlijk getal, is het bewijs makkelijk. Maar als je een x hebt die bijvoorbeeld ligt in het intervalquote:Op woensdag 18 januari 2012 17:40 schreef Anoonumos het volgende:
Is er iemand die me op weg kan hen helpen met deze vraag over continuiteit?
[ afbeelding ]


Goedenavond FOK!ers.
Ik snap deze vragen niet, eerst lukte het aardig maar ik ben het na de kerstvakantie weer helemaal kwijtgeraakt
Ik heb de blaadjes even gescanned.
http://img52.imageshack.us/img52/29/17012012443copycopy.jpg (copy/paste deze link)
http://img688.imageshack.us/img688/2536/17012012445copy.jpg (copy/paste deze link)
Groeten SlacKard
Ik snap deze vragen niet, eerst lukte het aardig maar ik ben het na de kerstvakantie weer helemaal kwijtgeraakt
Ik heb de blaadjes even gescanned.
http://img52.imageshack.us/img52/29/17012012443copycopy.jpg (copy/paste deze link)
http://img688.imageshack.us/img688/2536/17012012445copy.jpg (copy/paste deze link)
Groeten SlacKard
we cant feed the poor but we can fund a war


a) ABC is een rechthoekige driehoek. In een rechthoekige driehoek geldt de stelling van Pythagoras. De 'schuine zijde' is AC, dus
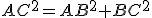
Hierin kun je de waardes van AB en BC invullen.
b) ABC is een rechthoekige driehoek. In een rechthoekige driehoek gelden de goniometrische identiteiten, samengevat als Sos-cas-toa. Stel dat je op punt A gaat staan en naar de driehoek kijkt, dan is AB de aanliggende rechthoekszijde, AC de overstaande rechthoekszijde en BC de schuine zijde. Omdat je AB en BC het nauwkeurigste weet, gebruik je de goniometrische identiteit waar o en a in voorkomen, dit is die van de tangens.
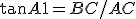 , verder invullen.
, verder invullen.
Hierin kun je de waardes van AB en BC invullen.
b) ABC is een rechthoekige driehoek. In een rechthoekige driehoek gelden de goniometrische identiteiten, samengevat als Sos-cas-toa. Stel dat je op punt A gaat staan en naar de driehoek kijkt, dan is AB de aanliggende rechthoekszijde, AC de overstaande rechthoekszijde en BC de schuine zijde. Omdat je AB en BC het nauwkeurigste weet, gebruik je de goniometrische identiteit waar o en a in voorkomen, dit is die van de tangens.


Das mooi om te horen, heb hier nog een blaadje met alle info over SOSCASTOA, dus dat komt goed.
we cant feed the poor but we can fund a war


Volgens mij had je net zo goed je boek even open kunnen slaan, luiwammesquote:
2000 light years from home


Nee want ik wist totaal de functie niet meer van de Stelling van Pythagoras, ik dacht dat het sinus was maar dan minder handig 
we cant feed the poor but we can fund a war


Als ik in SPSS een lineaire regressie uitvoer, dan vind ik het vreemd dat eigenlijk alles wel significant is. Ik heb een grote dataset.
Elke willekeurige combinatie van variabelen heeft een significant effect, de R^2 is daarentegen soms heel laag (0,0005) dus de onafhankelijke variabel verklaart vrijwel niks in de afhankelijke variabel.
Hoe kan het dat zowat alles significant is?
Elke willekeurige combinatie van variabelen heeft een significant effect, de R^2 is daarentegen soms heel laag (0,0005) dus de onafhankelijke variabel verklaart vrijwel niks in de afhankelijke variabel.
Hoe kan het dat zowat alles significant is?


4(1/4Q)2 = 1/4Q2, terwijl ik dacht dat het 1/2Q2 zou moeten zijn. Kan iemand mij het rekenregeltje uitleggen die ik blijkbaar vergeten ben?
Ik deed:
4(1/4Q)2
4(1/8Q2)
1/2Q2
Ik deed:
4(1/4Q)2
4(1/8Q2)
1/2Q2


