SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Nee, je integreert nu over een halve kubus in plaats van een halve bol.quote:Op woensdag 29 februari 2012 16:07 schreef Dale. het volgende:
[ afbeelding ]
Lijkt mij niet te kloppen?
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!
Ja dat dacht ik al idd 
maar hoe fix ik dat? Denk dat ik naar cillindercoordinaten (of bol) moet omzetten toch 
? Dus dan wordt het...
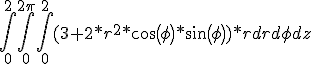
loopt van 0 naar 2, 
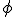is 360 graden, en 
is van 0 naar 2? Weet alleen [tex]\phi[/tex] niet zeker want dat kan ook 180 graden zijn? Omdat het een halve bol zeg maar is? Nee is fout want dat is eigenlijk een functie van 
en 
dus is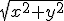 
... maar arg
[ Bericht 29% gewijzigd door Dale. op 29-02-2012 16:29:57 ]
maar hoe fix ik dat? Denk dat ik naar cillindercoordinaten (of bol) moet omzetten toch ? Dus dan wordt het...[ Bericht 29% gewijzigd door Dale. op 29-02-2012 16:29:57 ]
Op
z = r cos(phi) moet positief zijn, dus phi loopt van ...
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
True dus van -.5pi tot .5pi en theta is de cirkel dus van 0 tot 2pi i.p.v. tot pi.
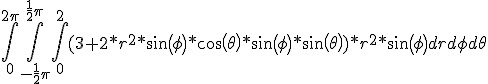
Maar dit moet toch makkelijker kunnen
?
[ Bericht 10% gewijzigd door Dale. op 29-02-2012 17:30:00 ]
Maar dit moet toch makkelijker kunnen
?[ Bericht 10% gewijzigd door Dale. op 29-02-2012 17:30:00 ]
Ik krijg er 16π uit. Zo dus. Je kunt gewoon in cartesische coördinaten blijven werken en het is met de hand te doen, maar ik ga het hier niet voor je uitschrijven.quote:
Maar dit moet toch makkelijker kunnen
Je eerste idee om x en y om te zetten naar poolcoördinaten en z te behouden is ook prima, maar je vergeet hierbij te bedenken dat het interval waarover r loopt afhangt van z. We hebben immers x2 + y2 + z2 ≤ 4 en dus r2 = x2 + y2 ≤ 4 - z2, zodat 0 ≤ r ≤ √(4 - z2). Je krijgt dan deze integraal, en de waarde daarvan is uiteraard ook 16π.
[ Bericht 13% gewijzigd door Riparius op 01-03-2012 16:34:57 ]
Nee, je mag ∞ niet als een getal behandelen, wat je hier doet heeft geen betekenis.quote:Op dinsdag 28 februari 2012 21:13 schreef Thas het volgende:
[..]
Daar kan ik nog wel inkomen, maar waarom is dit dan onbepaald, want dat is toch feitelijk hetzelfde?
Wil je limx→∞ xa/ex bepalen, bedenk dan dat je xa voor x > 0 kunt schrijven als ea∙ln(x), zodat:
(1) xa/ex = ea∙ln(x)∙e-x = ea∙ln(x) - x = e-x∙(1 - a∙ln(x)/x)
Nu is:
(2) limx→∞ ln(x)/x = 0,
en dus:
(3) limx→∞ e(1 - a∙ln(x)/x) = e1 = e,
zodat:
(4) limx→∞ xa/ex = limx→∞ (e(1 - a∙ln(x)/x))-x = limx→∞ e-x = 0.
Om in te zien dat (2) geldt kun je bedenken dat:
(5) ln(x) < x - 1 < x voor x > 1
En aangezien voor x > 1 ook ln(x) > 0 hebben we dus:
(6) ln(x)/x > 0 voor x > 1
Verder is ln(x)/x = ln((√x)2)/x = 2∙ln(√x)/x < 2∙(√x)/x voor x > 1, en dus:
(7) ln(x)/x < 2/√x voor x > 1
Uit (6) en (7) volgt nu:
(8) 0 < ln(x)/x < 2/√x voor x > 1,
en aangezien limx→∞ 2/√x = 0 volgt (2) uit (8) op grond van de insluitstelling.
[ Bericht 0% gewijzigd door Riparius op 01-03-2012 21:23:32 ]
Als je niet weet wat natuurlijke logaritmen zijn, zul je het antwoord van thenxzero niet begrijpen.quote:
Sorry hoor maar wat is In(a)Ik weet dat f(x)= 3x^2 wordt f'(x) = 6x, alleen deze snap ik niet.
Het verschil tussen die twee is dat bij 3x^2 de variabele op de grond staat en bij 3^x in de macht. Dus die kan je niet hetzelfde behandelen.quote:
Sorry hoor maar wat is In(a)
ln staat voor de natuurlijke logaritme, d.w.z. de logaritme met grondtal e.
Hmm... Dat zegt me niks eigenlijk. De opgave waar ik op vastloop is: gegeven is f(x) = 3^x. Bereken de hellimg van f voor x = -2. Het antwoord is f'(-2) = 0,122.
Ik heb alleen geen idee hoe ik dat zelf moet invullen.
Ik heb alleen geen idee hoe ik dat zelf moet invullen.
Je berekent de afgeleide van 3^x en in die afgeleide vul je voor x -2 in.
It's 106 miles to Chicago, we've got a full tank of gas, half a pack of cigarettes, its dark, and we're wearing sunglasses. Hit it.
Door het numerieke antwoord verwacht ik dat het met de GR moet.quote:
Hmm... Dat zegt me niks eigenlijk. De opgave waar ik op vastloop is: gegeven is f(x) = 3^x. Bereken de hellimg van f voor x = -2. Het antwoord is f'(-2) = 0,122.
Ik heb alleen geen idee hoe ik dat zelf moet invullen.
Daarvoor moet je de machtsregel toepassen:
Dus voor 3x wordt dat:
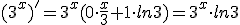
Vul x = -2 in en je zult 0.122068... als antwoord vinden.
Dus voor 3x wordt dat:
Vul x = -2 in en je zult 0.122068... als antwoord vinden.
Wtf wat vaag allemaal. Ik heb dit vorig jaar wel eens gehad maar zo ingewikkeld met die formules kan het toch niet zijn?
Voor een normale afgeleide kun je gewoon zeggen je doet de macht keer het voorste getal en trekt 1 van die macht af en dat is de afgeleide? En dat In komt me ook totaal onbekend voor.
Voor een normale afgeleide kun je gewoon zeggen je doet de macht keer het voorste getal en trekt 1 van die macht af en dat is de afgeleide? En dat In komt me ook totaal onbekend voor.
