[Bèta wiskunde] Huiswerk- en vragentopic

maandag 21 november 2011 @ 16:54:40 #81

thenxero

[ Bericht 52% gewijzigd door thenxero op 21-11-2011 17:45:03 ]

dinsdag 22 november 2011 @ 19:55:13 #82

Anoonumos

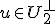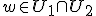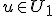Voor alle w geldt <w,x> = <w,y> = 0 voor alle $x \in U_1^\perp$ en alle $u \in U_2^\perp$ . Geldt dan dat $w \in U_1 \cap U_2$ ? Mijn gevoel zegt van niet, maar volgens mij heb ik dit wel nodig. Voor alle $x \in U_1^\perp$ geldt <x,u> = 0 voor alle $u \in U_1$ . Maar het lijkt dat als <w,x> = 0 dat w dan niet per se in 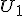$U_1$ zit?

dinsdag 22 november 2011 @ 20:22:05 #83

Anoonumos

Is al gelukt! (mbv $(S^\perp)^\perp = S$ . Excuses voor de dubbelpost maar mijn edit-knop werkt niet gek genoeg.

dinsdag 22 november 2011 @ 20:23:37 #84

GlowMouse

l'état, c'est moi

quote:
Op dinsdag 22 november 2011 20:22 schreef Anoonumos het volgende:
Is al gelukt! (mbv $(S^\perp)^\perp = S$ . Excuses voor de dubbelpost maar mijn edit-knop werkt niet gek genoeg.

zet je adblocker uit en/of leeg je browsercache

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

dinsdag 22 november 2011 @ 23:17:24 #85

gaussie

-

Ik zit met een probleem. Kan iemand me uitleggen wat het betekent dat de real projective line de boundary line van de upper half plane is? Ik begrijp de relatie tussen de real projective line en de upper half plane niet. Ik weet wel dat de real projective line topologisch equivalent is met een cirkel in R^2. Maar ik kan niet het verband leggen tussen de upper half plane en de real projective line. N.B. de upper half plane is een model voor hyperbolische meetkunde.

-

woensdag 23 november 2011 @ 00:09:12 #86

thenxero

Ik zou denken dat de boundary van de upper half plane de real line is en niet de real projective line...

woensdag 23 november 2011 @ 00:55:58 #87

thabit

't Is wel degelijk de projectieve lijn.

Het bovenhalfvlak is conform met de eenheidsschijf via de afbeelding z -> (z-i)/(z+i). De rand van de eenheidsschijf is de eenheidscirkel. Als we die afbeelding inverteren, dan krijgen we z -> i(z+1)/(1-z). Deze afbeelding beeldt de eenheidscirkel bijectief naar de projectieve lijn af. De verzameling punten behalve 1 wordt bijectief naar de reele lijn afgebeeld. Het punt 1 wordt afgebeeld naar het oneindige punt op de projectieve lijn. Ten opzichte van het bovenhalfvlak ligt dat punt oneindig ver verticaal omhoog. Alle verticale lijnen, die hyperbolisch ook lijnen zijn, gaan door dat randpunt.

woensdag 23 november 2011 @ 20:31:58 #88

JohnSpek

hoi

ik heb een schattingslijn y^ en de echte lijn y.
Hoe zorg ik ervoor dat y^ de vorm van y krijgt?

een negatieve lineaire term + kwadratische positieve term?

Ik weet het niet meer.

*Naar aanleiding van mijn post in het SPSS topic*

woensdag 23 november 2011 @ 20:33:59 #89

GlowMouse

l'état, c'est moi

Met een lineaire term en een kwadratische term zou je een eind kunnen komen. Positief/negatief bepaalt de OLS schatter.

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

woensdag 23 november 2011 @ 20:39:39 #90

JohnSpek

quote:
Op woensdag 23 november 2011 20:33 schreef GlowMouse het volgende:
Met een lineaire term en een kwadratische term zou je een eind kunnen komen. Positief/negatief bepaalt de OLS schatter.

Ik begrijp er geen reet van, want bij eigenlijk alles wat ik doe krijg ik een y = x lijn tussen de residuen en de afhankelijke variabel y. (wat dus niet mag..?)
Zelfs al doe ik x^6 en doe ik de regressie..

woensdag 23 november 2011 @ 20:53:27 #91

Sokz

Livin' the life

L'integrale

u = x⁵-1
du = 5xdx

Nu deed ik een voorbeeld uit 't boek na met iets andere getallen maar die deden dit:
'iets'

= 'iets' * 1/13 u¹³ + C
5x ......................................................................................... 5x

Maar wat moet ik in hemelsnaam voor dat 'iets' invullen .. volgens het antwoordenboek moest iets/5x 1/70 zijn mar als je dat terugrekent krijg je een onzinnig getal (1/13 * x = 1/70 » x = 5.3846 ... onzin)

woensdag 23 november 2011 @ 21:37:23 #92

Riparius

quote:
Op woensdag 23 november 2011 20:53 schreef Sokz het volgende:
L'integrale

[ afbeelding ]

u = x⁵-1
du = 5xdx

Nu deed ik een voorbeeld uit 't boek na met iets andere getallen maar die deden dit:
'iets' [ afbeelding ] = 'iets' * 1/13 u¹³ + C
5x ......................................................................................... 5x

Maar wat moet ik in hemelsnaam voor dat 'iets' invullen .. volgens het antwoordenboek moest iets/5x 1/70 zijn mar als je dat terugrekent krijg je een onzinnig getal (1/13 * x = 1/70 » x = 5.3846 ... onzin)

Als je nu eens begint te bedenken dat je hebt:

(x⁴ - x⁹)(x⁵ - 1)¹² = x⁴(1 - x⁵)(x⁵ - 1)¹² = -x⁴(x⁵ - 1)¹³

Nu zie je meteen dat je kunt substitueren:

u = x⁵ - 1

Dan is:

du/dx = 5x⁴

En dus:

du = 5x⁴dx

En dus:

(-1/5)∙du = -x⁴∙dx

Verder hebben we u = -1 voor x = 0 en u = 0 voor x = 1. De Integraal wordt dan:

∫_-1⁰ (-1/5)∙u¹³du = (-1/5)∙∫_-1⁰ u¹³du

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

donderdag 24 november 2011 @ 00:23:56 #93

Sokz

Livin' the life

Maar jij komt dus op ehm, 1/5 integr. en het antwoordenboek geeft 1/70 integr.

donderdag 24 november 2011 @ 00:39:43 #94

Riparius

quote:
Op donderdag 24 november 2011 00:23 schreef Sokz het volgende:
Maar jij komt dus op ehm, 1/5 integr. en het antwoordenboek geeft 1/70 integr.

Ik zal de uitwerking even afmaken. We krijgen dan:

(-1/5)∙∫_-1⁰ u¹³du = (-1/5)∙[(1/14)∙u¹⁴]_-1⁰ = (-1/5)∙(0 - 1/14) = 1/70, en dat klopt uiteraard.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

donderdag 24 november 2011 @ 16:48:57 #95

MWP

^__^

Nou ben ik niet echt een held in calculus, maar over het algemeen lukken opgaven mij toch altijd wel, maar bij deze kom ik er echt niet uit.

Express ln 0.25 in terms of ln 2 and ln 3.

Nou ben ik wel zover dat je e.e.a. kunt herschrijven als:
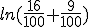$ln (\frac{16}{100} + \frac{9}{100})$ , en die 16 en 9 kan ik dan herschrijven als resp. 2⁴ en 3². Maar dan blijf ik met die 100 zitten...

Het is vast heel simpel, maar ik loop vast op die 100 geloof ik. Kan iemand mij weer op weg helpen?

donderdag 24 november 2011 @ 17:08:16 #96

GlowMouse

l'état, c'est moi

Je kunt direct met ln 1/4 werken, dan heb je ln3 niet nodig.

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

donderdag 24 november 2011 @ 17:18:36 #97

MWP

^__^

Zouden ze die vraag nou echt zo lullig hebben geformuleerd dat een antwoord met alleen ln 2 ook goed is?

donderdag 24 november 2011 @ 17:22:35 #98

GlowMouse

l'état, c'est moi

Er staat gewoon a*ln 2 (voor bepaalde a). Daar kun je alleen iets van maken waar ook ln3 in staat op een flauwe manier, zoals door 0*ln3 erbij op te tellen.

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

donderdag 24 november 2011 @ 17:30:18 #99

MWP

^__^

Wat enorm flauw. Ik heb me twee dagen uit de naad lopen schrijven om het in ln 2 én 3 uit te drukken. Zojuist -2 ln 2 ingevuld en voorwaar: "fantastic".

Bedankt!

vrijdag 25 november 2011 @ 23:02:31 #100

Dale.

Vraagje...

$gif.latex?\bigwedge_{i%20\in%20T^1}\bigg(\bigwedge_{\substack{j%20\in%20T^1%20\\%20j%20%3E%20i}}\bigg(\neg\big(s\langle%201%20\rangle%20\langle%20i\rangle%20=%20s%20\langle%201%20\rangle%20\langle%20j%20\rangle\big)%20\wedge%20\neg\big(s\langle%20i%20\rangle%20\langle%201\rangle%20=%20s%20\langle%20j%20\rangle%20\langle%201%20\rangle\big)\bigg)\bigg)$

Mag ik dit ook schrijven als... (http://en.wikipedia.org/wiki/Summation#Notation)

$gif.latex?\bigwedge_{\substack{i%20\in%20T^1%20\\%20j%20\in%20T^1%20\\%20j%20%3E%20i}}\bigg(\neg\big(s\langle%201%20\rangle%20\langle%20i\rangle%20=%20s%20\langle%201%20\rangle%20\langle%20j%20\rangle\big)%20\wedge%20\neg\big(s\langle%20i%20\rangle%20\langle%201\rangle%20=%20s%20\langle%20j%20\rangle%20\langle%201%20\rangle\big)\bigg)\bigg)$

Voor de goeie orde... $gif.latex?\bigwedge$ is de sommatie operator voor conjunction.

zaterdag 26 november 2011 @ 00:03:58 #101

thenxero

Sommatie van conjuctie? Ik neem aan dat je gewoon conjunctie bedoelt van alle elementen in de gegeven verzamelingen.

Volgens mij kan je dat wel zo opschrijven. Je mag vanwege associativiteit de volgorde van conjunctie veranderen, dus de tweede regel kan niet op verschillende manieren geïnterpreteerd worden.

zaterdag 26 november 2011 @ 00:59:26 #102

Dale.

quote:
Op zaterdag 26 november 2011 00:03 schreef thenxero het volgende:
Sommatie van conjuctie? Ik neem aan dat je gewoon conjunctie bedoelt van alle elementen in de gegeven verzamelingen.

Volgens mij kan je dat wel zo opschrijven. Je mag vanwege associativiteit de volgorde van conjunctie veranderen, dus de tweede regel kan niet op verschillende manieren geïnterpreteerd worden.

Ja weet niet hoe je dat noemt als je zeg maar 'sommeerd' over conjunctie maar gewoon conjunctie dus? "Je conjuctie over de elementen van ..." klinkt nogal raar tegenover ... Je sommeert over de elemente van ..."

zaterdag 26 november 2011 @ 13:39:38 #103

NonameNogame

Vraag mbt complexe getallen.

Gegeven:
|1 + i| = Wortel(2)
Arg(1+i) = pi / 4.

Waarom is Arg(1 + i) = pi / 4 ???

Ik kom namelijk uit op Arg 1 + i = 1, want tan arg(1 + i) = b / a = 1 / 1 = 1

Komt het doordat de argument Theta in RADIALEN uitgedrukt wordt?? Dus tan(pi / 4) = 1....klopt dit?

Maar dan zou ik tan-1 arg(w) moeten gebruiken toch?

In het boek staat als theorie:
If w = a + bi, where a = Re(w) != 0, then tan arg(w) = tan arg(a + bi) = b / a. (Dit snap ik allemaal)

Maar ik zit nu even in de knoop met wat tangens precies is, en wanneer je tangens gebruikt, en wanneer je tan-1 (inverse van tangens) gebruikt. Ik weet overigens dat tanx = sinx / cosx.

EDIT
Tan is een verhouding tussen sin en cos. Dus bij complexe getallen, geeft tan(arg(w)) de verhouding weer tussen sin(theta) en cos(theta). Indien deze verhouding 1 is, dan betekent dat de hoek (dus arg(w)) gelijk is aan pi/4.

Klopt dit?

[ Bericht 7% gewijzigd door NonameNogame op 26-11-2011 13:44:57 ]

zaterdag 26 november 2011 @ 14:01:46 #104

GlowMouse

l'état, c'est moi

Tangens is overstaande zijde gedeeld door aanliggende zijde. Hier: tan(arg(w)) = 1/1, dus arg(w) = tin^-1(1)

Kijk ook eens naar http://en.wikipedia.org/w(...)ustration_modarg.svg

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

zaterdag 26 november 2011 @ 14:12:59 #105

thenxero

quote:
Op zaterdag 26 november 2011 00:59 schreef Dale. het volgende:

[..]

Ja weet niet hoe je dat noemt als je zeg maar 'sommeerd' over conjunctie maar gewoon conjunctie dus? "Je conjuctie over de elementen van ..." klinkt nogal raar tegenover ... Je sommeert over de elemente van ..."

Dat heeft er waarschijnlijk mee te maken dat je dat laatste veel vaker hebt gehoord dan dat eerste.

zaterdag 26 november 2011 @ 14:23:39 #106

Snuf.

Zou iemand me uitkunnen leggen hoe ik de formule

quote:
K*L^-3/2

anders kan schrijven? Is dat dan?

quote:
K / (0.5*(sqrtL))

Of slaat dat nergens op?

Bedankt voor jullie hulp alvast.

zaterdag 26 november 2011 @ 14:31:42 #107

M.rak

quote:
Op zaterdag 26 november 2011 14:23 schreef Snuf. het volgende:
Zou iemand me uitkunnen leggen hoe ik de formule

[..]

anders kan schrijven? Is dat dan?

[..]

Of slaat dat nergens op?

Bedankt voor jullie hulp alvast.

Je zou 'm zo kunnen schrijven:

$K \cdot L^{-3/2} = \frac{K}{(L^{1/2})^3} = \frac{K}{(\sqrt{L})^3}$

The biggest argument against democracy is a five minute discussion with the average voter.

zaterdag 26 november 2011 @ 16:19:09 #108

GlowMouse

l'état, c'est moi

Of $\frac{K}{L\sqrt{L}$

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

zaterdag 26 november 2011 @ 16:27:29 #109

Snuf.

quote:
Op zaterdag 26 november 2011 16:19 schreef GlowMouse het volgende:
Of $\frac{K}{L\sqrt{L}$

quote:
Op zaterdag 26 november 2011 14:31 schreef M.rak het volgende:

[..]

Je zou 'm zo kunnen schrijven:

$K \cdot L^{-3/2} = \frac{K}{(L^{1/2})^3} = \frac{K}{(\sqrt{L})^3}$

Dankjulliewel, was even een beetje uit de wiskunde dus zag dit niet gelijk

zaterdag 26 november 2011 @ 17:27:29 #110

Riparius

quote:
Op zaterdag 26 november 2011 13:39 schreef NonameNogame het volgende:
Vraag mbt complexe getallen.

Gegeven:
|1 + i| = Wortel(2)
Arg(1+i) = pi / 4.

Waarom is Arg(1 + i) = pi / 4 ???

Kijk eens even hier en dan vooral dit plaatje. Voor a > 0 geldt Arg(a+bi) = arctan(b/a). Gebruik liever niet de (vooral Amerikaanse) notatie tan^-1x voor arctan x.

Edit: ik zie net dat je boek beweert dat dit ook zou gelden voor a < 0. Maar dat klopt niet. Om te beginnen is arg(z) voor een complex getal z (ongelijk aan nul) slechts bepaald tot op een geheel veelvoud van 2π. Je kunt dus niet zeggen dat arg(1+i) gelijk is aan ¼π. Wat wél correct is, is dat arg(1+i) = ¼π + 2kπ, k ∈ Z.

Vooral in angelsaksische literatuur wordt vaak onderscheid gemaakt tussen arg(z) en Arg(z), waarbij met het laatste de zogeheten 'hoofdwaarde' van het argument van z wordt aangegeven. Hiermee wordt doorgaans de unieke waarde van arg(z) op het interval (-π, π] bedoeld. En zo kunnen we dus inderdaad zeggen dat Arg(1+i) = ¼π. Maar omdat arctan(b/a) voor a,b ∈ R (a ≠ 0) alleen waarden op het interval (-½π, ½π) aanneemt, kan Arg(a+bi) dus alleen gelijk zijn aan arctan (b/a) voor a > 0.

[ Bericht 16% gewijzigd door Riparius op 27-11-2011 20:02:38 ]

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

maandag 28 november 2011 @ 15:36:43 #111

thenxero

Als A,B,C onafhankelijk exponentieel verdeeld zijn met parameters 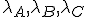$\lambda_A, \lambda_B, \lambda_C$ , wat is dan P(A<B<C) ?

Ik heb bedacht dat

P(A<B<C) = P(A<B<C | A=min{A,B,C}) P(A=min{A,B,C}) = P(B<C | A=min{A,B,C}) P(A=min{A,B,C}),

maar weet niet hoe ik verder kan.

maandag 28 november 2011 @ 15:53:48 #112

GlowMouse

l'état, c'est moi

P(A<B<C) = P({A < max{B,C}} en {B<C}) =P(A<max{B,C})P(B<C)

De verdeling van max{B,C} kun je zo bepalen, en dan zijn die kansen makkelijk uit te rekenen.

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

maandag 28 november 2011 @ 16:09:14 #113

thenxero

P(max{B,C} < x ) = P(B<x, C<x) = P(B<x) P(C<x)

Dus max{B,C} is Exp(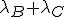 $\lambda_B + \lambda_C$ ) verdeeld.

edit: Thanks ik ben eruit

[ Bericht 18% gewijzigd door thenxero op 28-11-2011 16:23:12 ]

maandag 28 november 2011 @ 17:43:41 #114

GlowMouse

l'état, c'est moi

$\frac{\lambda_A}{\lambda_A + \lambda_B + \lambda_C} \frac{\lambda_B}{\lambda_B + \lambda_C}$
klopt dat?

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

maandag 28 november 2011 @ 17:59:29 #115

thenxero

quote:
Op maandag 28 november 2011 17:43 schreef GlowMouse het volgende:
$\frac{\lambda_A}{\lambda_A + \lambda_B + \lambda_C} \frac{\lambda_B}{\lambda_B + \lambda_C}$
klopt dat?

Ja precies. Ik had het ook nog op mijn eigen manier uitgerekend en gebruikt dat {B<C} onafhankelijk is van {A=min{A,B,C}} en daar kwam hetzelfde uit.

maandag 28 november 2011 @ 21:59:12 #116

Anoonumos

Ik probeer te bewijzen dat als:
(domein D in R, en punt c in D, en f:D -> R continu in c)
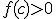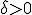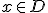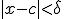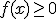Als $f(c) > 0$ dan bestaat er een $\delta > 0$ zo dat voor alle $x \in D$ met $|x-c| < \delta$ geldt dat $f(x) \geq 0$ .

Ik heb geprobeerd te werken met de definitie van continuiteit en dan f(c) als epsilon maar hiermee liep ik vast. Weet iemand of dit toch goed gaat of misschien een andere manier?

maandag 28 november 2011 @ 22:03:05 #117

GlowMouse

l'état, c'est moi

Je probeersel zou goed moeten gaan

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

maandag 28 november 2011 @ 22:13:30 #118

Anoonumos

Uit continuiteit volgt |f(x) - f(c)| < f(c) met f(c) > 0.
Als f(x) groter gelijk f(c) dan dus ook f(x) > 0.
Als f(x) < f(c) dan moet gelden:
f(c) - f(x) < f(c) dus f(x) > 0.

Dus f(x) groter gelijk 0.

Is dit correct of mis ik iets?

maandag 28 november 2011 @ 22:17:23 #119

GlowMouse

l'état, c'est moi

Je zegt nu niet hoe je aan x komt.

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

maandag 28 november 2011 @ 22:23:29 #120

Anoonumos

Uit continuiteit volgt dat voor alle x in het domein geldt |f(x) - f(c)| < f(c) met f(c) > 0. *

Forum Opties
Forumhop:
Hop naar:	(afkorting, bv 'KLB')

» school, studie en onderwijs

» school, studie en onderwijs