SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
De 2e vergelijking luidt #2=2/5#1+3/7#2quote:Op woensdag 5 oktober 2011 14:24 schreef Self-Catering het volgende:
[..]
Volgens mijn geen speciale tekens in de dit geval. Het zijn namelijk aantal stappen keer kans, zeg maar.
Dat is hetzelfde als 4/7#2=2/5#1
Oftewel, #2=7/10#1 en #1=10/7#2
En dan kan je hem zo invullen. Lukt het dan? Je krijgt in de bovenste vergelijking uiteindelijk 1 = ...#1 (of #2, of #3) en daarmee bereken je het antwoord.
Er staat trouwens toch wel "1" en geen "I"? Onduidelijk lettertype zeg, onhandig, nauwelijks verschil tussen hoofdletter i en 1.
Özil | Ki SY| Son HM| Lee SW| Taeguk Warriors|
Dank, maar zo ver was ik ookquote:
[..]
De 2e vergelijking luidt #2=2/5#1+3/7#2
Dat is hetzelfde als 4/7#2=2/5#1
Oftewel, #2=7/10#1 en #1=10/7#2
En dan kan je hem zo invullen. Lukt het dan? Je krijgt in de bovenste vergelijking uiteindelijk 1 = ...#1 (of #2, of #3) en daarmee bereken je het antwoord.
Als dat niet de bedoeling is heb ik trouwens geen idee
Wetende dat de antwoorden: #1 = 80/39 #2 = 56/39 #3 = 24/39, kom ik er nog niet uit
Of niet?
Als in, je snapt niet hoe ze bij die antwoorden zijn gekomen?quote:
[..]
Dank, maar zo ver was ik ook
Wetende dat de antwoorden: #1 = 80/39 #2 = 56/39 #3 = 24/39, kom ik er nog niet uit
Özil | Ki SY| Son HM| Lee SW| Taeguk Warriors|
Nou, eigenlijk niet nee. Want ik twijfel nu aan de stappen die ik maak. Oftwel, doe ik het goed?quote:
[..]
Als in, je snapt niet hoe ze bij die antwoorden zijn gekomen?
Of niet?
Het gaat dus zo:quote:
[..]
Nou, eigenlijk niet nee. Want ik twijfel nu aan de stappen die ik maak. Oftwel, doe ik het goed?
Je was zover dat je had #2=7/10#1 en #1=10/7#2. De derde vergelijking is #3=3/7#2.
Dan krijg je dus #3=3/7*(7/10*#1)=3/10#1.
Dat vul je in in vergelijking 1, dan krijg je:
#1=1+2/5#1+3/8*(3/10#1)
#1-2/5#1-3/8*3/10#1=1
39/80#1=1
#1=80/39
En dan vul je dat getal in en krijg je de antwoorden op #2 en #3.
Özil | Ki SY| Son HM| Lee SW| Taeguk Warriors|
Aight.quote:
[..]
Het gaat dus zo:
Je was zover dat je had #2=7/10#1 en #1=10/7#2. De derde vergelijking is #3=3/7#2.
Dan krijg je dus #3=3/7*(7/10*#1)=3/10#1.
Dat vul je in in vergelijking 1, dan krijg je:
#1=1+2/5#1+3/8*(3/10#1)
#1-2/5#1-3/8*3/10#1=1
39/80#1=1
#1=80/39
En dan vul je dat getal in en krijg je de antwoorden op #2 en #3.
[ Bericht 4% gewijzigd door Self-Catering op 05-10-2011 15:20:05 ]
Of niet?
Ik begrijp de volgende dingen niet:
1. Stel je hebt een continue kansdichtingsheidfunctie.
X = continue stochastische variabel
Y = continue stochastische variabel
Wat betekent:
E(E(X|Y is y))
In woorden betekent dit, volgens mij: De verwachtingswaarde van de verwachtingswaarde van (X met als voorwaarde dat Y gelijk is aan y). Maar ik begrijp niet meer wat ik dan precies aan het uitrekenen ben.
En waarom is dit gewoon gelijk aan de E(X).
2. Ook is dit misschien een domme vraag, maar stel ik heb een continue kansdichtheidsfunctie 8xy.
Wat betekent het dan precies als ik daar gewoon x = 0.4 en y = 0.4 invul? Wat zegt mijn antwoord dan?
3. Stel:
Kansdichtheidsfunctie:
8xy , 0 < x < y , 0 < y < 1
Ik wil de marginale kansdichtheidsfunctie van x.
Dit krijg ik door de integraal van 8xy (naar y, dus dy) te nemen, op het interval [1,x]. (volgens het boek).
In andere woorden, ik moet het domein van y (wat eerst 0 < y < 1 was) omschrijven naar een domein afhankelijk van x. Dit is (als ik een schets maak) [1, x].
Ik begrijp niet zo goed waarom ik het eerst moet omschrijven. Waarom mag ik y niet gewoon [0,1] laten en dan integreren. Ik begrijp dus blijkbaar niet echt goed wat ik hier doe omdat ik het antwoord hier niet op weet.
Alvast bedankt
1. Stel je hebt een continue kansdichtingsheidfunctie.
X = continue stochastische variabel
Y = continue stochastische variabel
Wat betekent:
E(E(X|Y is y))
In woorden betekent dit, volgens mij: De verwachtingswaarde van de verwachtingswaarde van (X met als voorwaarde dat Y gelijk is aan y). Maar ik begrijp niet meer wat ik dan precies aan het uitrekenen ben.
En waarom is dit gewoon gelijk aan de E(X).
2. Ook is dit misschien een domme vraag, maar stel ik heb een continue kansdichtheidsfunctie 8xy.
Wat betekent het dan precies als ik daar gewoon x = 0.4 en y = 0.4 invul? Wat zegt mijn antwoord dan?
3. Stel:
Kansdichtheidsfunctie:
8xy , 0 < x < y , 0 < y < 1
Ik wil de marginale kansdichtheidsfunctie van x.
Dit krijg ik door de integraal van 8xy (naar y, dus dy) te nemen, op het interval [1,x]. (volgens het boek).
In andere woorden, ik moet het domein van y (wat eerst 0 < y < 1 was) omschrijven naar een domein afhankelijk van x. Dit is (als ik een schets maak) [1, x].
Ik begrijp niet zo goed waarom ik het eerst moet omschrijven. Waarom mag ik y niet gewoon [0,1] laten en dan integreren. Ik begrijp dus blijkbaar niet echt goed wat ik hier doe omdat ik het antwoord hier niet op weet.
Alvast bedankt
1. De buitenste E is over Y, de binnenste over X.
2. dat betekent niets, een kansdichtheid moet je integreren om er betekenis aan toe te kennen.
3. het interval is [x,1]. Je moet eigenlijk doen:
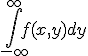
maar f(x,y) = 0 voor y die niet voldoen aan "0 < x < y , 0 < y < 1".
2. dat betekent niets, een kansdichtheid moet je integreren om er betekenis aan toe te kennen.
3. het interval is [x,1]. Je moet eigenlijk doen:
maar f(x,y) = 0 voor y die niet voldoen aan "0 < x < y , 0 < y < 1".
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Op vraag 3. Ohja, ik bedoelde inderdaad [x,1] , maar waarom zou ik het interval niet gewoon [0,1] kunnen laten? Waarom moet ik dit omschrijven in een interval afhankelijk van x (ik weet niet of ik dit goed zeg, maar je begrijpt hopelijk wat ik bedoel)quote:
1. De buitenste E is over Y, de binnenste over X.
2. dat betekent niets, een kansdichtheid moet je integreren om er betekenis aan toe te kennen.
3. het interval is [x,1]. Je moet eigenlijk doen:
maar f(x,y) = 0 voor y die niet voldoen aan "0 < x < y , 0 < y < 1".
Op vraag 2. Oke!
Op vraag 1. Ik begrijp nog niet helemaal wat je bedoelt.
Volgens mij bedoel je E(E(X|Y)). Omdat Y een stochast is, is de verwachtingswaarde van X gegeven Y nog afhankelijk van Y. Dus E(X|Y) kan je zien als een nieuwe stochast die door Y bepaald wordt. Van deze "nieuwe stochast" kan je dus weer de verwachtingswaarde bepalen.
Zie hier voor een bewijs dat het gelijk is aan E(X).
http://en.wikipedia.org/wiki/Expected_value#Iterated_expectation
Zie hier voor een bewijs dat het gelijk is aan E(X).
http://en.wikipedia.org/wiki/Expected_value#Iterated_expectation
Stel dat je het op [0,1] laat. Voor x=0.5 integreer je dan ook over het stuk y=[0,0.5], terwijl de kansdichtheid daar helemaal niet gegeven is door 8xy. Daar is de kansdichtheid gewoon 0. Maar omdat de integraal van 0 toch 0 is, laat je dat deel gewoon helemaal weg. Dan houd je [x,1] over.quote:
[..]
Op vraag 3. Ohja, ik bedoelde inderdaad [x,1] , maar waarom zou ik het interval niet gewoon [0,1] kunnen laten? Waarom moet ik dit omschrijven in een interval afhankelijk van x (ik weet niet of ik dit goed zeg, maar je begrijpt hopelijk wat ik bedoel)
Het is dus zoiets van:quote:
Volgens mij bedoel je E(E(X|Y)). Omdat Y een stochast is, is de verwachtingswaarde van X gegeven Y nog afhankelijk van Y. Dus E(X|Y) kan je zien als een nieuwe stochast die door Y bepaald wordt. Van deze "nieuwe stochast" kan je dus weer de verwachtingswaarde bepalen.
Zie hier voor een bewijs dat het gelijk is aan E(X).
http://en.wikipedia.org/wiki/Expected_value#Iterated_expectation
Je krijgt E(X|Y) door eerst de conditionele kansdichtheidsfunctie te bepalen, wat de joint kansdichtheidsfunctie is(8xy), geschaald naar de marginale kansdichtheidsfunctie van y.
Dat is dan 8xy/(4y^3) = 2x/y
Dat geeft mij dus een kansdichtheidsfunctie van x, als ik de variabel y zou invulle
Als ik dus de verwachtingswaarde van (2x/y) pak over alle mogelijke y waarden dan zou ik logischerwijs de verwachtingswaarde krijgen van x omdat ik voor elke y kijk wat mijn x waarden dan zou zijn.
Klopt deze gedachtegang een beetje?
Maar het hoeft niet weg gelaten te worden? Als de integraal toch 0 is dan maakt het voor het antwoord niet zoveel uit of je over [0,1] of [x,1] integreert?quote:
[..]
Stel dat je het op [0,1] laat. Voor x=0.5 integreer je dan ook over het stuk y=[0,0.5], terwijl de kansdichtheid daar helemaal niet gegeven is door 8xy. Daar is de kansdichtheid gewoon 0. Maar omdat de integraal van 0 toch 0 is, laat je dat deel gewoon helemaal weg. Dan houd je [x,1] over.
Maar de uitkomst is wel degelijk een andere functie. Als ik zou integeren over [0,1] dan zou het 4xy^2 = 4x zijn, terwijl het over [x,1] 4x - 4x^3 is.
[ Bericht 26% gewijzigd door JohnSpek op 05-10-2011 21:22:25 ]
Ja dat klopt wel.
Je berekent (in het discrete geval)
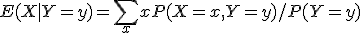
Dan vul je in plaats van y weer Y in, en dan neem je daar weer de verwachtingswaarde van.
Je berekent (in het discrete geval)
Dan vul je in plaats van y weer Y in, en dan neem je daar weer de verwachtingswaarde van.
Klopt, maar dan moet je dus een andere integrand nemen. De functie is op [0,x] gedefinieerd als 0, en op [x,1] gedefinieerd als 8xy.quote:
[..]
Maar het hoeft niet weg gelaten te worden? Als de integraal toch 0 is dan maakt het voor het antwoord niet zoveel uit of je over [0,1] of [x,1] integreert?
Wat je eigenlijk doet is, zoals GlowMouse zegt,
waarbij je dus de functie opdeelt in een deel waarin f=0, en een deel waarin f=8xy.
Oke, maar stel ik wil dus de kans weten dat 0 < X < 0.5. (en dit wil doen vanuit de marginale kansdichtheidsfunctie, gewoon als oefening).
Als ik 8xy integreer naar y over [1,x] dan komt daar 4x - 4x^3 uit. Dat integreren op 0 < X < 0.5
Dat zou dan zijn 2 * 0.5^2 - 0.5^4
Hoe zou ik dat doen als je gewoon het 0 stuk erbij laat als het waren?
(Dus als ik 8xy eerst integreer naar y over interval [0,1] om de marginale kansdichtheidsfunctie van x te bepalen)
Als ik 8xy integreer naar y over [1,x] dan komt daar 4x - 4x^3 uit. Dat integreren op 0 < X < 0.5
Dat zou dan zijn 2 * 0.5^2 - 0.5^4
Hoe zou ik dat doen als je gewoon het 0 stuk erbij laat als het waren?
(Dus als ik 8xy eerst integreer naar y over interval [0,1] om de marginale kansdichtheidsfunctie van x te bepalen)
Haakjes wegwerkenquote:Op woensdag 5 oktober 2011 21:45 schreef verwarmingsbank het volgende:
x(2x-3)=2(3x+1)
Wat is X? En wat is de berekening.
Klas: Atheneum 4
Ik heb het even voor je gepaint:
• Jij houdt nogal vast aan f(x,y)=8xy. Het punt is, dat dat alleen maar in het gearceerde gebied hierboven geldt. Daarbuiten is f(x,y) gelijk aan 0 - als het goed is staat dat ook zo gedefinieerd in je opgave.
• Wat doe je precies als je van 0 tot 1 integreert? Dan integreer je 8xy over de gehele blauwe lijn. Maar dat heeft geen zin, want op het b-gedeelte van de lijn is f(x,y) niet gelijk aan 8xy. Daarom heeft het alleen maar zin om over het a-gedeelte te integreren.
• Jij houdt nogal vast aan f(x,y)=8xy. Het punt is, dat dat alleen maar in het gearceerde gebied hierboven geldt. Daarbuiten is f(x,y) gelijk aan 0 - als het goed is staat dat ook zo gedefinieerd in je opgave.
• Wat doe je precies als je van 0 tot 1 integreert? Dan integreer je 8xy over de gehele blauwe lijn. Maar dat heeft geen zin, want op het b-gedeelte van de lijn is f(x,y) niet gelijk aan 8xy. Daarom heeft het alleen maar zin om over het a-gedeelte te integreren.
Dat begrijp ik, maar de uitkomst is steeds fout. Hoe moet ik deze doen volgens jullie?quote:
Op Iedereen aan wie ik het gevraagd heb begrijpt het niet bij mij op school.
Schrijf maar de stappen op die je al hebt gemaakt.quote:
[..]
Dat begrijp ik, maar de uitkomst is steeds fout. Hoe moet ik deze doen volgens jullie?
Iedereen aan wie ik het gevraagd heb begrijpt het niet bij mij op school.
x(2x-3)=2(3x+1)
2x² - 3x = 6x + 2
2x² -9x -2 = 0
x² - 4,5x -1 = 0
D=B²-4AC
D= (-4,5)² -4*1*1 = 16,25
X1 = (-b + Wortel van 16,25) / 2*1 = 4,27
X2 = (-b - Wortel van 16,25) / 2*1 = 0,23
2x² - 3x = 6x + 2
2x² -9x -2 = 0
x² - 4,5x -1 = 0
D=B²-4AC
D= (-4,5)² -4*1*1 = 16,25
X1 = (-b + Wortel van 16,25) / 2*1 = 4,27
X2 = (-b - Wortel van 16,25) / 2*1 = 0,23
Aha, ik had de tekening al wel gemaakt voor mezelf, maar nog niet zo naar gekekenquote:
Ik heb het even voor je gepaint:
[ afbeelding ]
• Jij houdt nogal vast aan f(x,y)=8xy. Het punt is, dat dat alleen maar in het gearceerde gebied hierboven geldt. Daarbuiten is f(x,y) gelijk aan 0 - als het goed is staat dat ook zo gedefinieerd in je opgave.
• Wat doe je precies als je van 0 tot 1 integreert? Dan integreer je 8xy over de gehele blauwe lijn. Maar dat heeft geen zin, want op het b-gedeelte van de lijn is f(x,y) niet gelijk aan 8xy. Daarom heeft het alleen maar zin om over het a-gedeelte te integreren.
Bedankt voor de moeite en uitleg! en xero/glowmouse ook bedankt ;
Je hebt gezegd C=1 terwijl het moet zijn C=-1.quote:
x(2x-3)=2(3x+1)
2x² - 3x = 6x + 2
2x² -9x -2 = 0
x² - 4,5x -1 = 0
D=B²-4AC
D= (-4,5)² -4*1*1 = 16,25
X1 = (-b + Wortel van 16,25) / 2*1 = 4,27
X2 = (-b - Wortel van 16,25) / 2*1 = 0,23
Bedankt voor de opmerking.
x(2x-3)=2(3x+1)
2x² - 3x = 6x + 2
2x² -9x -2 = 0
x² - 4,5x -1 = 0
D=B²-4AC
D= (-4,5)² -4*1*-1 = 24,25
X1 = (-b + Wortel van 24,25) / 2*1 = 4,71
X2 = (-b - Wortel van 24,25) / 2*1 = 0,21
Klopt dit dan wel
x(2x-3)=2(3x+1)
2x² - 3x = 6x + 2
2x² -9x -2 = 0
x² - 4,5x -1 = 0
D=B²-4AC
D= (-4,5)² -4*1*-1 = 24,25
X1 = (-b + Wortel van 24,25) / 2*1 = 4,71
X2 = (-b - Wortel van 24,25) / 2*1 = 0,21
Klopt dit dan wel
Je methode is goed. Als je je antwoord invult in x(2x-3)=2(3x+1) dan weet je of het antwoord ook klopt.quote:
Bedankt voor de opmerking.
x(2x-3)=2(3x+1)
2x² - 3x = 6x + 2
2x² -9x -2 = 0
x² - 4,5x -1 = 0
D=B²-4AC
D= (-4,5)² -4*1*-1 = 24,25
X1 = (-b + Wortel van 24,25) / 2*1 = 4,71
X2 = (-b - Wortel van 24,25) / 2*1 = 0,21
Klopt dit dan wel
En als tip voor de volgende keer om niet 2x² -9x -2 = 0 door twee te delen als je daarmee breuken krijgt. Want de abc-formule werkt ook prima met a=2.
Weet iemand een goede buitenlandse universiteit waar ze vakken als Statistics, Stochastic Integration, Lévy Processes, Financial Stochastics, Financial Time Series, Measure Theory, etc geven? Een master in Financial mathematics / stochastics dus.
Ik zit een beetje rond te kijken maar de UK is onbetaalbaar, en Duitse websites geven vaak vage of weinig informatie.
Ik zit een beetje rond te kijken maar de UK is onbetaalbaar, en Duitse websites geven vaak vage of weinig informatie.
Als ik X = 4,71 invul dan krijg ik 30,2382 = 30,26
Is zo'n klein verschil niet erg of wat doe ik nu weer fout
Is zo'n klein verschil niet erg of wat doe ik nu weer fout
Je weet pas echt zeker of het klopt als je het antwoord in "wortelvorm" laat staan, in plaats van numerieke benaderingen te gebruiken. Nu weet je alleen maar dat het waarschijnlijk goed is omdat een afwijking van 0,02 wel te verklaren is als je afrondt op 2 decimalen, maar zeker weten doe je niet.quote:
Als ik X = 4,71 invul dan krijg ik 30,2382 = 30,26
Is zo'n klein verschil niet erg of wat doe ik nu weer fout
Wow: in het antwoorden boekje staat dit:
9/4 - 1/4 Wortel 97 OF 9/4 - 1/4 Wortel 97
Oftewel er staat 2 keer hetzelfde getal
Wanneer ik dit trouwens in de rekenmachine gooi dan krijg ik uit:-0,2122
9/4 - 1/4 Wortel 97 OF 9/4 - 1/4 Wortel 97
Oftewel er staat 2 keer hetzelfde getal
Wanneer ik dit trouwens in de rekenmachine gooi dan krijg ik uit:-0,2122
één minnetje moet een plusje zijn. Dan krijg je -0,2122... en voor de andere 4.71221...quote:
Wow: in het antwoorden boekje staat dit:
9/4 - 1/4 Wortel 97 OF 9/4 - 1/4 Wortel 97
Oftewel er staat 2 keer hetzelfde getal
Wanneer ik dit trouwens in de rekenmachine gooi dan krijg ik uit:-0,2122
Volgende keer dus gewoon die wortel laten staan. Dan heb je een precies antwoord, en daar zijn wiskundigen altijd blij mee.
--------------
Even mijn laatste post naar beneden brengen:
quote:Weet iemand een goede buitenlandse universiteit waar ze vakken als Statistics, Stochastic Integration, Lévy Processes, Financial Stochastics, Financial Time Series, Measure Theory, etc geven? Een master in Financial mathematics / stochastics dus.
Ik zit een beetje rond te kijken maar de UK is onbetaalbaar, en Duitse websites geven vaak vage of weinig informatie.
[ Bericht 16% gewijzigd door thenxero op 05-10-2011 22:31:12 ]
Al die opgaven is aantonen voor 1 en dan voor k+1 aantonen met inductie, als je eenmaal 1 gehad hebt zijn ze allemaal hetzelfde.quote:
[..]
Is niet gespecificeerd maar bij de andere opgaven betekent deelbaar idd dat er een natuurlijk getal uitkomt.
Hoeveel tijd ben je trouwens tot nu toe voor alles kwijt?
En waarom was meneer Heij trouwens eigenlijk een week afwezig?
Beneath the gold, bitter steel
Ja ik heb ze nu allemaal gemaakt. Hoeveel tijd ik kwijt ben vind ik moeilijk te zeggen, ik doe nu zeg maar wat opgegeven staat en dat kost me ongeveer 20 uur per week, dus contact + zelfstudie. Alleen wil ik eigenlijk wel wat harder studeren voor de betere cijfers.quote:
[..]
Al die opgaven is aantonen voor 1 en dan voor k+1 aantonen met inductie, als je eenmaal 1 gehad hebt zijn ze allemaal hetzelfde.
Hoeveel tijd ben je trouwens tot nu toe voor alles kwijt?
En waarom was meneer Heij trouwens eigenlijk een week afwezig?
Hee jongens ik heb een vraag (joh, echt? 
)
ELx = X / √(ln(x2) - ln(y2)) * De afgeleide F(x,y) naar X. Maar ik kom niet uit die afgeleide volgens mij
Ik dacht dat de afgeleide 1/2(ln(x2) - ln(y2))-1/2 * (2x/x2) was maar dat weet ik niet zeker. Kan iemand mij helpen/vertellen of ik op de goede weg ben?
Alvast heel erg bedankt
)Dan doe ik eerst de partiele elasticiteit van x.quote:F(x,y) = √(ln(x2) - ln(y2)) (de hele formule staat dus onder de wortel)
Bepaal de partiële elasticiteit van F naar x en de partiële elasticiteit van F naar y en tel beide bij elkaar op.
ELx = X / √(ln(x2) - ln(y2)) * De afgeleide F(x,y) naar X. Maar ik kom niet uit die afgeleide volgens mij
Ik dacht dat de afgeleide 1/2(ln(x2) - ln(y2))-1/2 * (2x/x2) was maar dat weet ik niet zeker. Kan iemand mij helpen/vertellen of ik op de goede weg ben?
Alvast heel erg bedankt
Oke dankjewelquote:
De part. afgeleide is goed, twee keer de kettingregel gebruiken inderdaad.
Het uitwerken hiervan lukt me alleen niet zo goed, zou je misschien kunnen helpen?
Als ik die formule volg die je hebt geplaatst:
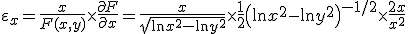
dan valt de 1/2 weg tegen de 2, valt de x^2 in de noemer weg tegen de twee factoren x in de teller. In de noemer houd je dan het kwadraat van een wortel over, dus
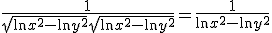
dan valt de 1/2 weg tegen de 2, valt de x^2 in de noemer weg tegen de twee factoren x in de teller. In de noemer houd je dan het kwadraat van een wortel over, dus
Super bedanktquote:
Als ik die formule volg die je hebt geplaatst:
dan valt de 1/2 weg tegen de 2, valt de x^2 in de noemer weg tegen de twee factoren x in de teller. In de noemer houd je dan het kwadraat van een wortel over, dus
Nevermind
Oh dus beide elasticiteiten optellen zal op 0 uitkomen?quote:
Nee, want je hebt daar nog een factor -1 staan bij de tweede keer dat je de kettingregel toepast.
