[Bèta wiskunde] Huiswerk- en vragentopic

donderdag 15 september 2011 @ 13:23:18 #31

GlowMouse

l'état, c'est moi

Dat kan niet algebraïsch.

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

donderdag 15 september 2011 @ 13:28:59 #32

keesjeislief

NextGenerationHippie

quote:
Op donderdag 15 september 2011 13:14 schreef maniack28 het volgende:
Ben even de weg kwijt, wie helpt?

De integraal van p(x) = A e^(-lamda(x-a)^2)

Moet ik de vermenigvuldiging in de e-macht (x-a)^2 eerst uitwerken naar x^2 -2ax+a^2 en dan de e-macht opdelen in verschillende stukken, los integreren en dan samenvoegen? Of is er een makkelijkere oplossing...

En sowieso.. wat was de integraal van e^(x^2) ook alweer?

Je kunt gebruiken dat

$\int_{\mathbb{R}} e^{-(x-\mu)^2/(2\sigma^2)} \, \mathrm{d}x = |\sigma| \sqrt{2\pi}$

voor elke $\mu \in \mathbb{R}$ en $\sigma \not= 0$ , vanwege de eigenschappen van de normale verdeling.

heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek

donderdag 15 september 2011 @ 14:05:17 #33

maniack28

Dresden Dolls O+

Sorry ik was vergeten te vermelden dat ik dan wil integreren van -oneindig tot +oneindig

Dank keesjeislief!

Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.

donderdag 15 september 2011 @ 14:49:32 #34

maniack28

Dresden Dolls O+

Ik zal wel een kneus zijn... maar als ik nu <x> wil berekenen, dus de integraal over -oneindig tot +oneindig van x*p(x) dx met p(x)=A e^(-lamda(x-a)^2), hoe doe ik dat dan?

_{voelt zich geen wiskundig wonder}

Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.

donderdag 15 september 2011 @ 16:03:58 #35

Haushofer

Substitutie: noem u = -\lambda(x-a)^2, dan du -2\lambda(x-a) dx.

Dit kun je altijd doen als de macht van x in de exponent 1 hoger is dan de macht van x in de integraal

Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071

donderdag 15 september 2011 @ 16:14:36 #36

Maryn.

mm

quote:
Op donderdag 15 september 2011 03:36 schreef Riparius het volgende:

[..]

Inzicht is beter dan regeltjes leren over wat 'mag' en 'niet mag'. Als je hebt:

1/p = 1/q,

waarbij we p en q beiden ongelijk aan nul veronderstellen, omdat de breuken anders geen betekenis hebben, en we vermenigvuldigen beide leden met het product pq, dan krijgen we:

pq/p = pq/q.

Nu is de breuk in het linkerlid te vereenvoudigen tot q/1 = q omdat teller en noemer een factor p gemeen hebben, en de breuk in het rechterlid is te vereenvoudigen tot p/1 = p omdat teller en noemer een factor q gemeen hebben. En dus resulteert inderdaad q = p oftewel p = q.

Ik vat 'm nog niet helemaal.

als ik heb 1/s = (T-t)/tT hoe krijg ik dan s = tT/T-t (uit antwoordboek)?

donderdag 15 september 2011 @ 16:53:52 #37

Siddartha

quote:
Op donderdag 15 september 2011 16:14 schreef Maryn. het volgende:

[..]

Ik vat 'm nog niet helemaal.

als ik heb 1/s = (T-t)/tT hoe krijg ik dan s = tT/T-t (uit antwoordboek)?

Weet je wat kruiselings vermenigvuldigen is?

Of:

Weet je waarom je beide kanten met een getal(of letter!) mag vermenigvuldigen?

donderdag 15 september 2011 @ 17:06:11 #38

Maryn.

mm

quote:
Op donderdag 15 september 2011 16:53 schreef Siddartha het volgende:

[..]

Weet je wat kruiselings vermenigvuldigen is?

Of:

Weet je waarom je beide kanten met een getal(of letter!) mag vermenigvuldigen?

Via kruislings heb ik hem nu opgelost.. thanks, maar wat bedoel je met dat laatste? * S?

donderdag 15 september 2011 @ 17:30:37 #39

Siddartha

quote:
Op donderdag 15 september 2011 17:06 schreef Maryn. het volgende:

[..]

Via kruislings heb ik hem nu opgelost.. thanks, maar wat bedoel je met dat laatste? * S?

Jij had de vergelijking:
1/s = (T-t)/tT
Je weet dus dat s,t en T niet nul zijn (waarom?), dus kun je beide kanten bijvoorbeeld met s vermenigvuldigen:
1=s(T-t)/tT
Vermenigvuldig beide kanten nu met tT/(T-t) (of anders gezegd: Deel beide kanten door (T-t)/tT) ,dan krijg je:
tT/(T-t)=s
En dus weet je wat s is.

Je kunt een vergelijking aan beide kanten met een getal/letter vermenigvuldigen zolang het maar niet 0 is. Net zo mag je aan beide kanten iets toevoegen. Denk er maar eens over na, neem de vergelijking :
x=10
Vermenigvuldig beide kanten maar eens met een getal, of tel aan beide kanten iets op. Wat belangrijk is, is dat x daardoor niet verandert! Dat gebeurt wel als je die vermenigvuldiging of optelling maar aan één kant doet. Dat is ook logisch:
x=10 en niet x=10+2 of x-3=10.
En dit kun je dus met elke vergelijking doen.

donderdag 15 september 2011 @ 17:48:03 #40

Sokz

Livin' the life

volgende som (sqrt in een sqrt) staat gelijk aan C.
1....
1+R - A ............ = C
1....
1+R + B

Hoe krijg ik R hieruit? (let niet op de puntjes)

wat heb ik tot dusverre geprobeert:

A/B = C » A = C
A/B - C = 0 en dan verder uitwerken (kom ik ook niet verder)
A/B * B = C*B » A = CB kump ik ook niet verder

donderdag 15 september 2011 @ 18:32:59 #41

maniack28

Dresden Dolls O+

quote:
Op donderdag 15 september 2011 16:03 schreef Haushofer het volgende:
Substitutie: noem u = -\lambda(x-a)^2, dan du -2\lambda(x-a) dx.

Dit kun je altijd doen als de macht van x in de exponent 1 hoger is dan de macht van x in de integraal

Amen... ik blijf dit soort dingen lastig vinden... practice makes perfect I guess.

Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.

donderdag 15 september 2011 @ 18:44:06 #42

Djoezt

Argumentative with the face on

Weet iemand toevallig hoe ik deze recursieve definitie om kan schrijven naar een directe formule? Het is een beetje weggezakt, en een huisgenoot doet een één of ander bedrijfskundevak waar 't relevant is. Met een recursief programma kan ik 't nog wel oplossen bij n = 40, maar met het handje op 't tentamen is 't nogal wat werk..

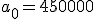
$a_0 = 450000$
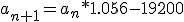
$a_{n+1} = a_n * 1.056 - 19200$

donderdag 15 september 2011 @ 19:03:24 #43

M.rak

quote:
Op donderdag 15 september 2011 17:48 schreef Sokz het volgende:
volgende som (sqrt in een sqrt) staat gelijk aan C.
1....
1+R - A ............ = C
1....
1+R + B

Hoe krijg ik R hieruit? (let niet op de puntjes)

wat heb ik tot dusverre geprobeert:

A/B = C » A = C
A/B - C = 0 en dan verder uitwerken (kom ik ook niet verder)
A/B * B = C*B » A = CB kump ik ook niet verder

Dit is de opgave toch?

$\frac{\frac{1}{1+R}-A}{\frac{1}{1+R}+B}=C$

Eerst vermenigvuldigen we dan de teller en de noemer met 1+R:

$\frac{1-A-AR}{1+B+BR}=C$

Dan vermenigvuldigen we links en rechts met 1+B+BR:

$1-A-AR=C+B+BCR$

Dan halen we de termen met R naar een kant:

$BCR+AR=1-A-C-B$

Dan halen we R buiten haakjes:

$R(BC+A)=1-A-C-B$

En dan delen we door BC+A

$R=\frac{1-A-C-B}{BC+A}$

The biggest argument against democracy is a five minute discussion with the average voter.

donderdag 15 september 2011 @ 19:31:06 #44

Snuf.

Hee jongens, ik heb weer een vraag

Kan iemand mij helpen met dit?

Bepaal de inverse functie van

N = f(L) = 1

Hoe zoek ik dan uit wat L is?

donderdag 15 september 2011 @ 19:56:06 #45

thenxero

quote:
Op donderdag 15 september 2011 18:44 schreef Djoezt het volgende:
Weet iemand toevallig hoe ik deze recursieve definitie om kan schrijven naar een directe formule? Het is een beetje weggezakt, en een huisgenoot doet een één of ander bedrijfskundevak waar 't relevant is. Met een recursief programma kan ik 't nog wel oplossen bij n = 40, maar met het handje op 't tentamen is 't nogal wat werk..

$a_0 = 450000$
$a_{n+1} = a_n * 1.056 - 19200$

In het algemeen:
Stel a₀ = b en a_n+1 = c a_n + d.

Dan krijg je dus
a₁ = c a₀ + d = cb + d
a₂ = c a₁ + d = c(cb+d) + d = c²b + cd + d
a₃ = c a₂ + d = c(c(cb+d)+d) + d = c³b + c² d + cd + d

Aan het patroon zie je dat je dan krijgt
a_n = cⁿ b + c^n-1 d + ... + c¹d + d

donderdag 15 september 2011 @ 19:57:19 #46

thenxero

quote:
Op donderdag 15 september 2011 19:31 schreef Snuf. het volgende:
Hee jongens, ik heb weer een vraag

Kan iemand mij helpen met dit?

Bepaal de inverse functie van

N = f(L) = 1

Hoe zoek ik dan uit wat L is?

Wat is f, wat is L, wat is N?

donderdag 15 september 2011 @ 19:58:38 #47

Sokz

Livin' the life

quote:
Op donderdag 15 september 2011 19:03 schreef M.rak het volgende:

[..]

Dit is de opgave toch?

$\frac{\frac{1}{1+R}-A}{\frac{1}{1+R}+B}=C$

Eerst vermenigvuldigen we dan de teller en de noemer met 1+R:

$\frac{1-A-AR}{1+B+BR}=C$

Dan vermenigvuldigen we links en rechts met 1+B+BR:

$1-A-AR=C+B+BCR$

Dan halen we de termen met R naar een kant:

$BCR+AR=1-A-C-B$

Dan halen we R buiten haakjes:

$R(BC+A)=1-A-C-B$

En dan delen we door BC+A

$R=\frac{1-A-C-B}{BC+A}$

donderdag 15 september 2011 @ 19:59:06 #48

Djoezt

Argumentative with the face on

quote:
Op donderdag 15 september 2011 19:56 schreef thenxero het volgende:

[..]

In het algemeen:
Stel a₀ = b en a_n+1 = c a_n + d.

Dan krijg je dus
a₁ = c a₀ + d = cb + d
a₂ = c a₁ + d = c(cb+d) + d = c²b + cd + d
a₃ = c a₂ + d = c(c(cb+d)+d) + d = c³b + c² d + cd + d

Aan het patroon zie je dat je dan krijgt
a_n = cⁿ b + c^n-1 d + ... + c¹d + d

Daar was ik me van bewust (met een sigmanotatie is het nog best overzichtelijk) maar dat lost het probleem nog niet op: n = 40 zonder grafische rekenmachine / computer

donderdag 15 september 2011 @ 20:30:50 #49

GlowMouse

l'état, c'est moi

Jawel, want je kunt de som van een meetkundige reeks makkelijk berekenen.

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

vrijdag 16 september 2011 @ 00:01:48 #51

GlowMouse

l'état, c'est moi

10^{-2.5}

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

vrijdag 16 september 2011 @ 00:02:09 #52

Riparius

quote:
Op vrijdag 16 september 2011 00:00 schreef magneetstrip het volgende:
Hoe bereken je de inverse logaritme van -2,5 ? (scheikunde, iets met pH en concentratie)

Aangenomen dat je logaritmen met grondtal 10 bedoelt, is dat dus gewoon een macht van 10 ...

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

vrijdag 16 september 2011 @ 00:12:46 #53

Djoezt

Argumentative with the face on

quote:
Op donderdag 15 september 2011 20:30 schreef GlowMouse het volgende:
Jawel, want je kunt de som van een meetkundige reeks makkelijk berekenen.

Ik zie 't nog niet helemaal geloof ik

vrijdag 16 september 2011 @ 00:13:16 #54

GlowMouse

l'état, c'est moi

quote:
Op vrijdag 16 september 2011 00:02 schreef Riparius het volgende:

[..]

Aangenomen dat je logaritmen met grondtal 10 bedoelt, is dat dus gewoon een macht van 10 ...

Welk positief reëel getal niet?

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

vrijdag 16 september 2011 @ 00:15:06 #55

GlowMouse

l'état, c'est moi

quote:
Op vrijdag 16 september 2011 00:12 schreef Djoezt het volgende:

[..]

Ik zie 't nog niet helemaal geloof ik

Je kunt a_n = cⁿ b + c^n-1 d + ... + c¹d + d schrijven als:
a_n = cⁿ b + (c^n-1 + ... + c¹ + c⁰)d
= cⁿ b + (cⁿ - c⁰) / (c-1) * d

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

vrijdag 16 september 2011 @ 16:49:06 #56

Maryn.

mm

72 -(4+x)² - (4-rx)²
Ik wil deze omzetten naar de quadratic function.
Dus ax +bx² + c

Ik begin zo:
72 - [ (4+x)(4+x) ] - [ (4-rx)(4+rx) ]

72 - (16+4x+4x+x²) - (16 + 4rx - 4rx +r²x²)

72 - 16 - 8x - x² - 16 - 4rx + 4rx + r²x²

40 - 8x - x² + r²x²

Dit gaat volgens mij niet helemaal goed want ik mis 8rx..
Iemand weet waar ik foutje maak? En hoe ik het beste verder kan gaan om in die vorm te krijgen?

vrijdag 16 september 2011 @ 17:07:45 #57

freiss

Hertog Jan :9~

quote:
Op vrijdag 16 september 2011 16:49 schreef Maryn. het volgende:
72 -(4+x)² - (4-rx)²
Ik wil deze omzetten naar de quadratic function.
Dus ax +bx² + c

Ik begin zo:
72 - [ (4+x)(4+x) ] - [ (4-rx)(4+rx) ]

72 - (16+4x+4x+x²) - (16 + 4rx - 4rx +r²x²)

72 - 16 - 8x - x² - 16 - 4rx + 4rx + r²x²

40 - 8x - x² + r²x²

Dit gaat volgens mij niet helemaal goed want ik mis 8rx..
Iemand weet waar ik foutje maak? En hoe ik het beste verder kan gaan om in die vorm te krijgen?

Je schrijft (4-rx)² verkeerd uit, dus de eerste regel gaat al fout. Verder doe je het wel goed.

HJ 14-punt-gift.
Lijst met rukmateriaal!

vrijdag 16 september 2011 @ 17:28:25 #58

thenxero

Standaardnotatie is trouwens ax² + bx + c ipv ax +bx² + c

vrijdag 16 september 2011 @ 17:32:31 #59

Haushofer

quote:
Op donderdag 15 september 2011 18:32 schreef maniack28 het volgende:

[..]

Amen... ik blijf dit soort dingen lastig vinden... practice makes perfect I guess.

Een aardige site is b.v. SOS Math Calculus, en voor jou dan het kopje "TECHNIQUES OF INTEGRATION". Staan de meeste truukjes en handigheidjes wel op

Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071

vrijdag 16 september 2011 @ 17:35:45 #60

Maryn.

mm

72 - [ (4+x)(4+x) ] - [ (4-rx)(4-rx) ]

72 - (16+4x+4x+x²) - (16 - 4rx - 4rx - r²x²)

72 - 16 - 8x - x² - 16 + 4rx + 4rx - r²x²

40 - 8x + 8rx - x² - r²x²

-(r² -1)x² + 8(r-1)x - 40

Dus a = (r² -1)
en b = 8(r-1)

maar dan klopt ie niet dus wordt het dit toch?:

-(r² -1)x² + 8(r-1)x² + 40

Forum Opties
Forumhop:
Hop naar:	(afkorting, bv 'KLB')

» school, studie en onderwijs

» school, studie en onderwijs