SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Vorige deel: [Bèta wiskunde] Huiswerk-en-vragentopic
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
• http://betahw.mine.nu/index.php: site van GlowMouse om formules te kunnen gebruiken in je posts (op basis van Latexcode wordt een plaatje gegenereerd dat je vervolgens via het aangegeven linkje kunt opnemen).
Een uitleg over LaTeX-code kun je hier vinden, en je kunt deze site gebruiken om een hele post met verschillende stukken Latex-code erin ineens te laten parsen door betahw.mine.nu.
Wiskundig inhoudelijk:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
• http://betahw.mine.nu/index.php: site van GlowMouse om formules te kunnen gebruiken in je posts (op basis van Latexcode wordt een plaatje gegenereerd dat je vervolgens via het aangegeven linkje kunt opnemen).
Een uitleg over LaTeX-code kun je hier vinden, en je kunt deze site gebruiken om een hele post met verschillende stukken Latex-code erin ineens te laten parsen door betahw.mine.nu.
Wiskundig inhoudelijk:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Ah ja, ik las het verkeerd. Ik neem aan dat n=2 en bewijs het in dat geval. Even proberen.
Aan minibeer: a|b betekent a deelt b, oftewel b/a zit in Z. Staat ook (in iets andere vorm en algemener) gedefinieerd op p3!
Aan minibeer: a|b betekent a deelt b, oftewel b/a zit in Z. Staat ook (in iets andere vorm en algemener) gedefinieerd op p3!
Niet helemaal equivalent: 0 deelt 0, maar 0/0 is niet gedefinieerd.quote:Op zondag 10 april 2011 16:53 schreef BasementDweller het volgende:
Aan minibeer: a|b betekent a deelt b, oftewel b/a zit in Z. Staat ook (in iets andere vorm) gedefinieerd op p3!
Ik kom er echt niet uit...
Misschien toch wel
Klopt het dat E(X1² X2 + X1X2²) = 0?
[ Bericht 42% gewijzigd door BasementDweller op 10-04-2011 17:45:50 ]
Misschien toch wel
Klopt het dat E(X1² X2 + X1X2²) = 0?
[ Bericht 42% gewijzigd door BasementDweller op 10-04-2011 17:45:50 ]
Dat is uiteraard de bedoeling, anders is de opgave fout. Je wilde het echter met karakteristieke functies doen, in dat opzicht is E(X1² X2 + X1X2²) niet de juiste stap.
Ja dat is waar. Maar ik dacht misschien dat ik deze dan weer kan bewijzen met karakteristieke functies maar dat lukte me niet.quote:
Dat is uiteraard de bedoeling, anders is de opgave fout. Je wilde het echter met karakteristieke functies doen, in dat opzicht is E(X1² X2 + X1X2²) niet de juiste stap.
Je kan het derde moment van de som uitdrukken in karakteristieke functies, en de karakteristieke functie van de som van twee onafhankelijke stochasten in elk van beide.
thanks thabit en basementdweller
Ah, ik heb gezegd f_X1+X2 = f_X1 f_X2, en dat ding 3x naar t gedifferentieerd. Na heel vaak de productregel van differentiëren toegepast te hebben komt het antwoord eruit. Bedankt.quote:
Je kan het derde moment van de som uitdrukken in karakteristieke functies, en de karakteristieke functie van de som van twee onafhankelijke stochasten in elk van beide.
Dat "heel vaak toepassen" daar bestaat ook een binomium voor:
http://en.wikipedia.org/wiki/Product_rule#Higher_derivatives
http://en.wikipedia.org/wiki/Product_rule#Higher_derivatives
Chique, bedankt.quote:Op zondag 10 april 2011 19:52 schreef thabit het volgende:
Dat "heel vaak toepassen" daar bestaat ook een binomium voor:
[ afbeelding ]
http://en.wikipedia.org/wiki/Product_rule#Higher_derivatives
Om even terug naar trigonometrie te gaan: Klopt deze afleiding?
tan(x/2) = sinx / (1 + cosx)
stel sinx = p => arcsin(sinx) = x = arcsin(p)
tan(x/2) = p / (1 + SQRT(1-p2)
arctan(tan(x/2)) = arctan (p / (1 + SQRT(1-p2))
(x/2) = arctan (p / (1 + SQRT(1-p2))
x = 2 arctan (p / (1 + SQRT(1-p2))
backsub x = arcsin(p)
arcsin p = 2 arctan (p / (1 + SQRT(1-p2))
tan(x/2) = sinx / (1 + cosx)
stel sinx = p => arcsin(sinx) = x = arcsin(p)
tan(x/2) = p / (1 + SQRT(1-p2)
arctan(tan(x/2)) = arctan (p / (1 + SQRT(1-p2))
(x/2) = arctan (p / (1 + SQRT(1-p2))
x = 2 arctan (p / (1 + SQRT(1-p2))
backsub x = arcsin(p)
arcsin p = 2 arctan (p / (1 + SQRT(1-p2))
Da's enkel een kwestie van domeinrestrictie. En dat had je zelf al kunnen zien aan de wortelterm waarin x in [-1,1] moet liggen, anders is deze niet gedefinieerd. En laat [-1,1] nou net het complete domein van arcsin (en arccos) zijnquote:
Nee, arcsin(sin x) is niet x: als je bij x 2pi optelt, blijft z'n sinus immers hetzelfde.
[ Bericht 14% gewijzigd door VanishedEntity op 10-04-2011 20:57:17 ]
Ja, logisch dat je dan niet uitkomt, want je gaat voorbij aan de extra eis van domeinrestrictie die bij cyclometrische functies naar voren komt. 2pi valt niet binnen het domein [-1/2*pi;1/2*pi] voor sinx, en daarmee het bereik van arcsinx. Je zal eerst net zolang INT*2pi af moeten trekken totdat x, òf pi - x binnen [-1/2*pi;1/2*pi] komt te liggen.quote:
Vul maar x=2pi in: arcsin(sin 2pi) = 0, niet x.
Ola, ik zit ook even met een probleempje.
Als ik de volgende dubbele integraal oplos
I(a) = int(int(exp(-a(x+2*y)), y = x .. 1), x = 0 .. 1)
kom ik voor willekeurige a uit op
I(a) = (1/6)*(2*exp(-3*a)-3*exp(-2*a)+1)/a^2
vervolgens moet ik laten zien dat dit voor a=0 gelijk is aan een half, maar gezien je deelt door 0² heb je toch een ongedefinieerde oplossing, of ben ik nu een kiwi?
kusjes
Als ik de volgende dubbele integraal oplos
I(a) = int(int(exp(-a(x+2*y)), y = x .. 1), x = 0 .. 1)
kom ik voor willekeurige a uit op
I(a) = (1/6)*(2*exp(-3*a)-3*exp(-2*a)+1)/a^2
vervolgens moet ik laten zien dat dit voor a=0 gelijk is aan een half, maar gezien je deelt door 0² heb je toch een ongedefinieerde oplossing, of ben ik nu een kiwi?
kusjes
Omnia vincit amor, nos et cedamus amori
direct a invullen in de integraal dan kom je inderdaad uit op een half, maar de opdracht is vervolgens op I(a) voor willekeurige a te bepalen en dan komt de vraag op beide manieren overeen komen
Omnia vincit amor, nos et cedamus amori
Ik heb iets dat me helemaal gek maakt. Ik ben bezig met zelfstudie voor Wiskunde B en heb niemand in mijn omgeving die me dit uitleggen. Het volgende vraag ik me af:
Bron: http://www.wetenschapsforum.nl/index.php?showtopic=6783
Deze formule draait om het afgeleide van f(x) = x2. Allemaal duidelijk, totdat ik bij derde stap van de formule kom. Daar komt h2 + 2hx wat mij betreft een beetje uit de lucht vallen. Ik weet dat de afgeleide van X2 = 2X, maar dat verklaart niet hoe men komt tot de derde stap.
Kan iemand mij uitleggen wat hier nou precies gebeurd. Mijn boek, Youtube en andere sites geven me geen duidelijkheid. Overigens heb ik het voorbeeld van internet gehaald, aangezien dat duidelijker is dan mijn boek.
Bron: http://www.wetenschapsforum.nl/index.php?showtopic=6783
Deze formule draait om het afgeleide van f(x) = x2. Allemaal duidelijk, totdat ik bij derde stap van de formule kom. Daar komt h2 + 2hx wat mij betreft een beetje uit de lucht vallen. Ik weet dat de afgeleide van X2 = 2X, maar dat verklaart niet hoe men komt tot de derde stap.
Kan iemand mij uitleggen wat hier nou precies gebeurd. Mijn boek, Youtube en andere sites geven me geen duidelijkheid. Overigens heb ik het voorbeeld van internet gehaald, aangezien dat duidelijker is dan mijn boek.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
vlogens mij wordt (x + h)^2 daar gewoon uitgeschrevenquote:
Ik heb iets dat me helemaal gek maakt. Ik ben bezig met zelfstudie voor Wiskunde B en heb niemand in mijn omgeving die me dit uitleggen. Het volgende vraag ik me af:
[ afbeelding ]
Bron: http://www.wetenschapsforum.nl/index.php?showtopic=6783
Deze formule draait om het afgeleide van f(x) = x2. Allemaal duidelijk, totdat ik bij derde stap van de formule kom. Daar komt h2 + 2hx wat mij betreft een beetje uit de lucht vallen. Ik weet dat de afgeleide van X2 = 2X, maar dat verklaart niet hoe men komt tot de derde stap.
Kan iemand mij uitleggen wat hier nou precies gebeurd. Mijn boek, Youtube en andere sites geven me geen duidelijkheid. Overigens heb ik het voorbeeld van internet gehaald, aangezien dat duidelijker is dan mijn boek.
Dus zonder haakjes 
Zie je het dan wel? Schrijf gewoon maar eens uit.
~Si vis amari, ama~
(x+h)2= x2+2xh+h2quote:
Ik heb iets dat me helemaal gek maakt. Ik ben bezig met zelfstudie voor Wiskunde B en heb niemand in mijn omgeving die me dit uitleggen. Het volgende vraag ik me af:
[ afbeelding ]
Bron: http://www.wetenschapsforum.nl/index.php?showtopic=6783
Deze formule draait om het afgeleide van f(x) = x2. Allemaal duidelijk, totdat ik bij derde stap van de formule kom. Daar komt h2 + 2hx wat mij betreft een beetje uit de lucht vallen. Ik weet dat de afgeleide van X2 = 2X, maar dat verklaart niet hoe men komt tot de derde stap.
Kan iemand mij uitleggen wat hier nou precies gebeurd. Mijn boek, Youtube en andere sites geven me geen duidelijkheid. Overigens heb ik het voorbeeld van internet gehaald, aangezien dat duidelijker is dan mijn boek.
Als je dit optelt met die -x2 krijg je 2xh+h2
Niet altijd serieus
Heb je wel eens gehoord van een merkwaardig product?quote:
Ik heb iets dat me helemaal gek maakt. Ik ben bezig met zelfstudie voor Wiskunde B en heb niemand in mijn omgeving die me dit uitleggen. Het volgende vraag ik me af:
[ afbeelding ]
Bron: http://www.wetenschapsforum.nl/index.php?showtopic=6783
Deze formule draait om de afgeleide van f(x) = x2. Allemaal duidelijk, totdat ik bij derde stap van de formule kom. Daar komt h2 + 2hx wat mij betreft een beetje uit de lucht vallen. Ik weet dat de afgeleide van x2 = 2x, maar dat verklaart niet hoe men komt tot de derde stap.
Kan iemand mij uitleggen wat hier nou precies gebeurt. Mijn boek, Youtube en andere sites geven me geen duidelijkheid. Overigens heb ik het voorbeeld van internet gehaald, aangezien dat duidelijker is dan mijn boek.
Eigenlijk niet.quote:
[..]
Heb je wel eens gehoord van een merkwaardig product?
Ik mis nogal wat algebraïsche kennis heb ik gemerkt. Ben er nu naar een het kijken. Erg verhelderend allemaal.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Ik ben nu wat aan het leren over o.a. modulorekenen, en er staan wat opdrachten bij. Ik kan maar niet uit deze komen:
zoek de gehele getallen waarvoor x2-3y2=1997
Volgens wolfram heeft deze vergelijking geen oplossingen, maar het lukt me niet dit zelf aan te tonen. Het lukt me wel bijvoorbeeld de vergelijking a-3b=1997 op te lossen (wat dan ook niet zo moeilijk is), maar ik snap niet goed hoe je dit moet doen.
Als iemand een tip heeft hoor ik het graag.
zoek de gehele getallen waarvoor x2-3y2=1997
Volgens wolfram heeft deze vergelijking geen oplossingen, maar het lukt me niet dit zelf aan te tonen. Het lukt me wel bijvoorbeeld de vergelijking a-3b=1997 op te lossen (wat dan ook niet zo moeilijk is), maar ik snap niet goed hoe je dit moet doen.
Als iemand een tip heeft hoor ik het graag
.
Finally, someone let me out of my cage
Het merkwaardig product dat je in je bepaling van de afgeleide van f(x) = x2 kunt gebruiken is:quote:
[..]
Eigenlijk niet.
(a + b)2 = a2 + 2ab + b2
Je kunt de juistheid van deze identiteit natuurlijk aantonen door de haakjes in het linkerlid weg te werken, maar het is meetkundig ook mooi in te zien dat dit klopt.
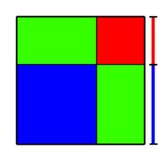
De oppervlakte van een vierkant met zijde a is a2 en de oppervlakte van een vierkant met zijde b is b2. Stel nu eens dat we een vierkant hebben met zijde (a + b), dan is de oppervlakte (a + b)2. Maar hoe staat deze oppervlakte nu in verband met die van de vierkanten met zijde a en zijde b? Ik heb even een plaatje gepikt uit de Franse Wikipedia:
Laten we aannemen dat het blauwe lijnstuk rechts van het vierkant een lengte a heeft, en het rode lijnstuk een lengte b. Dan is de totale zijde van het vierkant dus (a + b) en de totale oppervlakte van het vierkant dus (a + b)2. Maar je ziet dat de totale oppervlakte van het grote vierkant wordt gevormd door het blauwe vierkant (met oppervlakte a2), het rode vierkant (met oppervlakte b2), maar ook nog door de twee groene rechthoeken. Elk van die groene rechthoeken heeft een lengte a en een breedte b, en dus een oppervlakte ab. En omdat er twee van die rechthoeken zijn, moeten we bij a2 + b2 dus ook nog 2ab optellen om de oppervlakte van het grote vierkant te krijgen. En dat is precies wat het merkwaardig product hierboven zegt!
ok, laten we gewoon eens wat gaan rekenen en kijken hoever we komen:quote:
Ik ben nu wat aan het leren over o.a. modulorekenen, en er staan wat opdrachten bij. Ik kan maar niet uit deze komen:
zoek de gehele getallen waarvoor x2-3y2=1997
Volgens wolfram heeft deze vergelijking geen oplossingen, maar het lukt me niet dit zelf aan te tonen. Het lukt me wel bijvoorbeeld de vergelijking a-3b=1997 op te lossen (wat dan ook niet zo moeilijk is), maar ik snap niet goed hoe je dit moet doen.
Als iemand een tip heeft hoor ik het graag
x2-3y2=1997
3y2=x2-1997
y2=(x2-1997)/3
Nu maken we de observatie dat als dit een oplossing heeft voor x en y gehele getallen, dan moet x2-1997 deelbaar zijn door 3. met andere woorden:
x2 = 1997 mod 3
Aan jou de vraag, waarom heeft dit geen oplossing?
Feitelijk is het dus zo dat X2 = 2X omdat het twee (blauwe) vierkanten vormt? Tenminste om het even eenvoudig te maken voor mezelf, want volgens mij klopt dat niet helemaal.quote:
[..]
... En dat is precies wat het merkwaardig product hierboven zegt!
[ Bericht 3% gewijzigd door Pipo1234 op 12-04-2011 12:34:29 ]
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
x2 is sowieso niet gelijk aan 2x, de afgeleide van x2 is 2x. Dat is ook niet zo omdat het twee blauwe vierkanten vormt (los daarvan, er is maar één blauw vierkant), dat is slechts een tussenstap die je nodig hebt om de limiet op te lossen.quote:
[..]
Feitelijk is het dus zo dat X2 = 2X omdat het twee (blauwe) vierkanten vormt? Tenminste om het even eenvoudig te maken voor mezelf, want volgens mij klopt dat niet helemaal.
Het vierkant laat zien dat je (a+b)2 kunt schrijven als a2+2ab+b2. Als je dat invult in de limiet kom je uit op de oplossing
.Je moet het niet te simpel maken voor jezelf door stappen simpelweg over te slaan, dan klopt het niet meer.
The biggest argument against democracy is a five minute discussion with the average voter.
quote:
[..]
x2 is sowieso niet gelijk aan 2x, de afgeleide van x2 is 2x. Dat is ook niet zo omdat het twee blauwe vierkanten vormt (los daarvan, er is maar één blauw vierkant), dat is slechts een tussenstap die je nodig hebt om de limiet op te lossen.
Het vierkant laat zien dat je (a+b)2 kunt schrijven als a2+2ab+b2. Als je dat invult in de limiet kom je uit op de oplossing
Je moet het niet te simpel maken voor jezelf door stappen simpelweg over te slaan, dan klopt het niet meer.
Het is de afgeleide natuurlijk. Misschien probeer ik het inderdaad te simpel voor mezelf te maken.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Die merkwaardige producten is precies wat ik nodig had! Alleen nu heb ik er nog een vraag over. Als ik X3 heb en dan op h3 + 3x2h + 3xh2 uitkom, wat gebeurd er dan met die overtollige 3x van de laatste samenstelling? Als ik h wegstreep houd ik namelijk 3x over... en ik weet dat het antwoord 3x2 moet zijn.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Ik begrijp niet precies wat je bedoelt? Als ik het uitwerk kom ik uit op(h3 + 3x2h + 3xh2 + x3 - x3)/h. Als je dat uitwerkt komt het gewoon uit hoorquote:
Die merkwaardige producten is precies wat ik nodig had! Alleen nu heb ik er nog een vraag over. Als ik X3 heb en dan op h3 + 3x2h + 3xh2 uitkom, wat gebeurd er dan met die overtollige 3x van de laatste samenstelling? Als ik h wegstreep houd ik namelijk 3x over... en ik weet dat het antwoord 3x2 moet zijn.
. Misschien dat je vergeten bent om in het begin f(x+h) - f(x) te doen?
The biggest argument against democracy is a five minute discussion with the average voter.
Nee die formule heb ik ook. Ik probeer het te gebruiken voor een differentatie van X3. Bij X2 kom ik er door H weg te strepen. Maar bij X3 houd ik op de volgende manier 3X2 en 3X over: h3 + 3x2h + 3xh2 + x3 - x3)/hquote:
[..]
Ik begrijp niet precies wat je bedoelt? Als ik het uitwerk kom ik uit op(h3 + 3x2h + 3xh2 + x3 - x3)/h. Als je dat uitwerkt komt het gewoon uit hoor
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Ah, nu begrijp ik het denk ik:quote:
[..]
ok, laten we gewoon eens wat gaan rekenen en kijken hoever we komen:
x2-3y2=1997
3y2=x2-1997
y2=(x2-1997)/3
Nu maken we de observatie dat als dit een oplossing heeft voor x en y gehele getallen, dan moet x2-1997 deelbaar zijn door 3. met andere woorden:
x2 = 1997 mod 3
Aan jou de vraag, waarom heeft dit geen oplossing?
x2 = 1997 mod 3
x2 = 2 mod 3
De enige manier om in modulo 3 verzameling 2 te krijgen is door 1 met 2 of 2 met 1 te vermenigvuldigen. Voor x2 is er us geen oplossing in gehele getallen.
Dit betekent als ik het goed begrijp ook dat x2 -2 nooit deelbaar is door 3, wat ik best opmerkelijk vind
.Dank voor de hulp
Finally, someone let me out of my cage
Ik denk dat je de limiet van h naar 0 vergeet. Je deelt een keer een h weg, zodat je h2 + 3xh + 3x2 overhoudt. De limiet van h naar 0 nemen zorgt er voor dat alleen de 3x2 overblijft.quote:
[..]
Nee die formule heb ik ook. Ik probeer het te gebruiken voor een differentatie van X3. Bij X2 kom ik er door H weg te strepen. Maar bij X3 houd ik op de volgende manier 3X2 en 3X over: h3 + 3x2h + 3xh2 + x3 - x3)/h
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!
Ik snap dat even niet. Betekent dit dat de lim h->0 de 3xh2 wegstreept omdat deze 0 is? Er zit toch 3X in, of is dat 3xh en geen 3x?quote:Op dinsdag 12 april 2011 15:29 schreef freiss het volgende:
[..]
Ik denk dat je de limiet van h naar 0 vergeet. Je deelt een keer een h weg, zodat je h2 + 3xh + 3x2 overhoudt. De limiet van h naar 0 nemen zorgt er voor dat alleen de 3x2 overblijft.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Even tussendoor, snap je wat er bedoelt wordt met de limiet? Dat is namelijk wel redelijk belangrijk om dit echt te begrijpenquote:
[..]
Ik snap dat even niet. Betekent dit dat de lim h->0 de 3xh2 wegstreept omdat deze 0 is? Er zit toch 3X in, of is dat 3xh en geen 3x?
. Ik zal proberen uit te leggen wat er gebeurt, eerst heb je de limiet van (f(x+h) - f(x) )/h. Daarna schrijf je dit uit, in jouw geval krijg je dan de limiet van (h3 + 3x2h + 3xh2 + x3 - x3)/h. Eerst werk je dit uit, je deelt de h weg uit alle termen, je krijgt nu de limiet van h2 + 3x2 + 3xh. Nu ga je de limiet invullen, als h in deze uitdrukking naar nul gaat zullen alle termen nul worden behalve 3x2, dat is dus de uitkomst van dit probleem. Ik ben er in deze uitleg een beetje van uitgegaan dat je snapt wat de limiet is, als je dat niet snapt moet je dat maar even proberen op te zoeken of te vragen
.
The biggest argument against democracy is a five minute discussion with the average voter.
Differentiëren is geen 'wegstrepen'. Je bepaalt van een functie y = f(x) eerst het differentiequotiënt:quote:Op dinsdag 12 april 2011 15:58 schreef Pipo1234 het volgende:
[..]
Ik snap dat even niet. Betekent dit dat de lim h->0 de 3xh2 wegstreept omdat deze 0 is? Er zit toch 3X in, of is dat 3xh en geen 3x?
Δy/Δx = (f(x+h) - f(x))/((x+h) - x) = (f(x+h) - f(x))/h
Deze verhouding zegt iets over hoeveel de afhankelijke variabele y (i.e. de functiewaarde) verandert in verhouding tot een verandering van de onafhankelijke variabele x. Meetkundig kun je dit opvatten als de gemiddelde steilheid van de curve van f(x) over een klein intervalletje [x, x+h]. Door nu het intervalletje steeds kleiner te maken (en dus de limiet te bepalen als h naar 0 gaat) krijgen we dan de steilheid van de curve van f(x) c.q. de steilheid van de raaklijn aan de curve van f(x) in één bepaald punt. Die steilheid (en dus de afgeleide) is een maat voor de snelheid waarmee de waarde van f(x) op dat punt verandert.
Hebben we f(x) = x3, dan vinden we voor het differentiequotiënt:
(f(x+h) - f(x))/h = ((x+h)3 - x3)/h = (x3 + 3x2h + 3xh2 + h3 - x3)/h = 3x2 + 3xh + h2
Om nu de afgeleide f'(x) te vinden moet ik de limiet van dit differentiequotiënt bepalen voor h→ 0. Dus krijg ik:
f'(x) = lim h→0 (f(x+h) - f(x))/h = lim h→0 (3x2 + 3xh + h2) = 3x2
De beide termen 3xh en h2 naderen immers tot 0 als we h naar nul laten gaan, zodat 3x2 resulteert.
quote:
[..]
Ik snap dat even niet. Betekent dit dat de lim h->0 de 3xh2 wegstreept omdat deze 0 is? Er zit toch 3X in, of is dat 3xh en geen 3x?
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
